-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Optics and Applications
p-ISSN: 2168-5053 e-ISSN: 2168-5061
2013; 3(6): 119-124
doi:10.5923/j.optics.20130306.01
About the Definition of “Multiplier” of an Integrating Sphere
Antonio Parretta1, 2, Gabriele Calabrese2
1ENEA Research Centre “E. Clementel”, Via Martiri di Monte Sole 4, Bologna, 40129, Italy
2Physics Department, University of Ferrara, Via Saragat 1, Ferrara, 44122, Italy
Correspondence to: Antonio Parretta, ENEA Research Centre “E. Clementel”, Via Martiri di Monte Sole 4, Bologna, 40129, Italy.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
The definition of “sphere multiplier” or “sensitivity factor” of an integrating sphere is revisited by comparing the radiance of the integrating sphere with the radiance of the planar diffuser obtained by unfolding the integrating sphere surface. We get to two new definitions of “sphere multiplier”, derived by a different choice of “input flux” to the integrating sphere: a collimated flux impinging on a small region of the sphere wall in the first case; a diffused flux impinging on the total surface of the sphere in the second one. The two definitions of “sphere multiplier” differ by a factor equal to the reflectivity of the first impact region of the collimated beam.
Keywords: Sphere multiplier, Integrating sphere, Light diffuser, Radiance
Cite this paper: Antonio Parretta, Gabriele Calabrese, About the Definition of “Multiplier” of an Integrating Sphere, International Journal of Optics and Applications, Vol. 3 No. 6, 2013, pp. 119-124. doi: 10.5923/j.optics.20130306.01.
Article Outline
1. Introduction
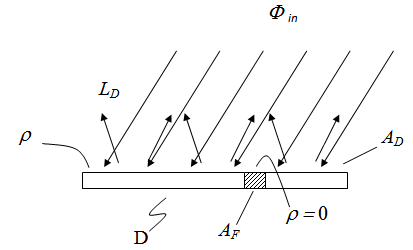
- The integrating sphere has a relevant role in optics as it can be used as a light source with constant radiance or as a linear device for radiation measurements[1]. The integrating sphere has been widely used by us for the optical characterization of photovoltaic materials and devices and for radiation measurements on concentrated solar beams [2-17]. The theory of radiation emitted by an illuminated integrating sphere brings to the definition of the so called “sphere multiplier” M, a parameter which accounts for the increase of radiance, due to the internal multiple reflections, with respect to a planar diffuser with the same surface area. In what follows, we refer to the theory of integrating sphere as reported in refs.[18-21]. In this theory, the radiance LD of a planar diffuser of total area AD, without openings, and reflectivity ρ:
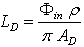 | (1) |
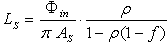 | (2) |
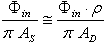 | (3) |
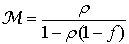 | (4) |
2. Alternative Definitions of “Sphere Multiplier”
- To make a correct comparison between the integrating sphere and the corresponding planar diffuser, we fix the same area in both cases and imagine that the integrating sphere surface be unfolded to realize the planar surface of the diffuser. Let us consider at first the simple case of a sphere of total area AS, composed of an optically uniform wall surface and some ports with zero reflectivity for the input and output of radiation. The unfolded sphere gives rise to a planar diffuser (d) of total area AD = AS and some openings of area AF = f · AS (see Figure 1) where f is the fraction of openings area. If the surface has ideal diffusing properties, that is has a Lambertian behaviour, then the radiance LD (W m-2 sr-1) of the planar diffuser is constant with viewing direction and can be expressed as follows:
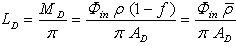 | (5) |
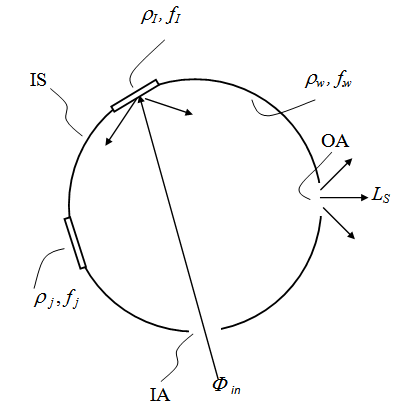
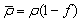 is the average reflectivity of the diffuser.To calculate the radiance LS of the integrating sphere (is), we refer to Figure 2. The (is) is irradiated by a collimated beam with the same flux Φin as before, entering the sphere through the input aperture (IA) and impinging on a small region (first impact region) of the internal wall. The radiance LS is that measured from the radiation emitted by the output aperture (oa) of the sphere, and is obtained by the irradiance EW produced on the internal wall at the stationary state, following the relation:
is the average reflectivity of the diffuser.To calculate the radiance LS of the integrating sphere (is), we refer to Figure 2. The (is) is irradiated by a collimated beam with the same flux Φin as before, entering the sphere through the input aperture (IA) and impinging on a small region (first impact region) of the internal wall. The radiance LS is that measured from the radiation emitted by the output aperture (oa) of the sphere, and is obtained by the irradiance EW produced on the internal wall at the stationary state, following the relation: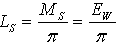 | (6) |
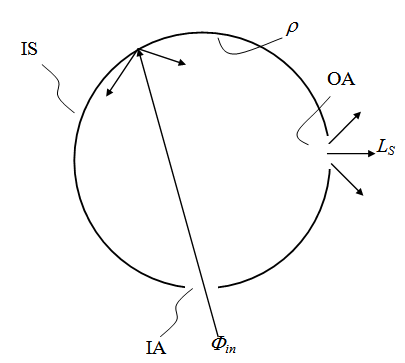 | Figure 2. The integrating sphere (IS) is irradiated by the flux Φin at input port (IA) and produces a flux with constant radiance LS at output port (OA) |
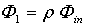 | (7) |
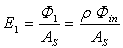 | (8) |
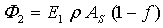 | (9) |
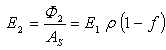 | (10) |
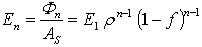 | (11) |
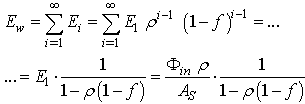 | (12) |
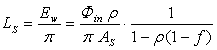 | (13) |
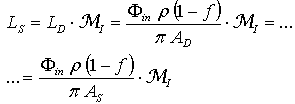 | (14) |
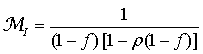 | (15) |
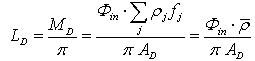 | (16) |
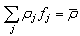 is the average reflectance of the diffuser and of the sphere.As regards the integrating sphere, we distinguish the first impact region, of fraction area fI and reflectivity ρI, from the other portions of the sphere surface. Equation (8) becomes:
is the average reflectance of the diffuser and of the sphere.As regards the integrating sphere, we distinguish the first impact region, of fraction area fI and reflectivity ρI, from the other portions of the sphere surface. Equation (8) becomes: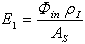 | (17) |
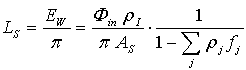 | (18) |
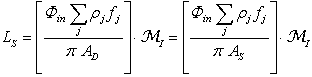 | (19) |
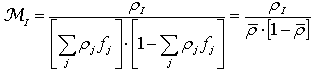 | (20) |
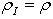 and
and 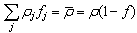 , being ρ the reflectivity of the sphere wall. Eq.s (16), (18) and (20) are strictly valid in the hypothesis that all the portions of the sphere have a Lambertian behavior. In practice, this is well satisfied by the high reflectivity wall surface, less well by the surface of the accessories faced to the sphere interior. In this paper we want to introduce a new definition of sphere multiplier, indicated as MII. Considering the way how the planar diffuser and the integrating sphere are illuminated in the so far discussed approach, in fact, we note that the surface is uniformly illuminated by the input beam in the first device, whereas the input beam illuminates only the first impact region in the second one. To make a more congruent comparison between the radiance of the two devices, therefore, we should compare the diffused flux incident on the planar diffuser with the diffused flux produced into the integrating sphere after the first reflection. In this new point of view, instead of putting equal the flux
, being ρ the reflectivity of the sphere wall. Eq.s (16), (18) and (20) are strictly valid in the hypothesis that all the portions of the sphere have a Lambertian behavior. In practice, this is well satisfied by the high reflectivity wall surface, less well by the surface of the accessories faced to the sphere interior. In this paper we want to introduce a new definition of sphere multiplier, indicated as MII. Considering the way how the planar diffuser and the integrating sphere are illuminated in the so far discussed approach, in fact, we note that the surface is uniformly illuminated by the input beam in the first device, whereas the input beam illuminates only the first impact region in the second one. To make a more congruent comparison between the radiance of the two devices, therefore, we should compare the diffused flux incident on the planar diffuser with the diffused flux produced into the integrating sphere after the first reflection. In this new point of view, instead of putting equal the flux 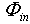 at input in the two devices, we put equal the diffused flux incident on the diffuser with the diffused flux incident on the integrating sphere wall surface soon after the reflection on the first impact region. We change, therefore, the flux at input of the sphere
at input in the two devices, we put equal the diffused flux incident on the diffuser with the diffused flux incident on the integrating sphere wall surface soon after the reflection on the first impact region. We change, therefore, the flux at input of the sphere 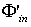 in order to have
in order to have 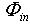 as the first diffused flux on the total area
as the first diffused flux on the total area 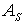 :
: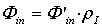 | (21) |
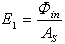 | (22) |
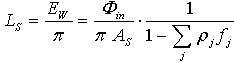 | (23) |
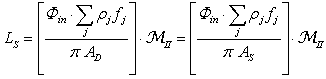 | (24) |
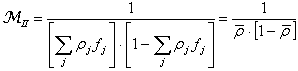 | (25) |
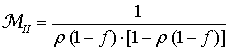 | (26) |
3. Optical Simulations
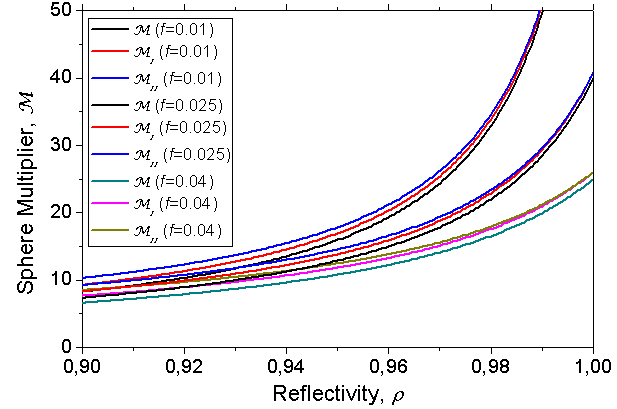
- To highlight the difference between the new definitions of sphere multiplier, expressed by Eq.s (15), (20), (25) and (26), and the old definition expressed by Eq. (4), some optical simulations have been carried out taking into account realistic values for the optical parameters of the sphere. We consider a simple sphere composed of a homogeneous inner wall with reflectivity ρ and some windows for the input and output of the light, covering altogether a fraction area equal to f . These two parameters are sufficient to apply Eq.s (4), (15) and (26) for calculating the three sphere multipliers.Figure 4 shows the sphere multipliers M, MI and MII calculated as a function of the reflectivity ρ , varying in the 0.9-1.0 interval, for three different values of the fraction area f : 0.01, 0.025 and 0.04. The value f = 0.04 is the maximum tolerated for assuring an optimal integration of light inside the sphere[19]. The reflectivity scale was extended to 1.00, but this is just a theoretical limit, not reachable in practice, as the best values of ρfor lambertian mirrors are around 0.99[19-21]. Figure 4 shows that for f = 0.01 the multipliers reach values as high as 50, and well higher values can be reached further reducing f. It is interesting to note the strong effect that the parameter f produces on the multipliers at high values of ρ. From Eq.s (4), (15) and (26), in fact, we can note that, in the limit ρ= 1, the multipliers depend only on f; in particular, M converges to 1/f, while MI and MII converge to 1/[f(1-f)], which are very close each other for very small values of f. A minor effect is instead produced by the different definitions of M. This effect is best appreciated by exploring lower values of ρ, as reported in Figure 5, where the three multipliers are shown for f = 0.01 and 0.04 as function of reflectivity ρ varying in the 0.8-0.95 interval. From Figure 5 we see that all the three multipliers tend to be less dependent on f at decreasing ρ in the examined, realistic range for the wall reflectivity of an integrating sphere. We see also that the old multiplier M shows the lowest values, the new multiplier MII shows the highest ones, and finally the new multiplier MI shows intermediate values between them. Both the new definitions of sphere multiplier, therefore, determine improved values over the old definition. The multiplier MII is 1/ρ times MI , as established by Eq.s (15) and (26); this is due to the fact that the definition of MI requires one more reflection on the wall, that one of the collimated beam at input, to produce the same diffused flux which is considered as input flux for the definition of MII . This explains why the two quantities converge to the same value when ρ approaches the unity. Contrary to what may seem from Figure 5, the three multipliers tend to very different limits when ρ tends to zero. This is shown in Figure 6. For low values of ρ , M, MI and MII , go as ρ , (1+f) and 1/ρ , respectively. The examination of the range of low values of ρ is only speculative, since in practice the values of wall reflectivity in an integrating sphere vary in the range 0.8-0.99, depending on the fabrication process of the coating.
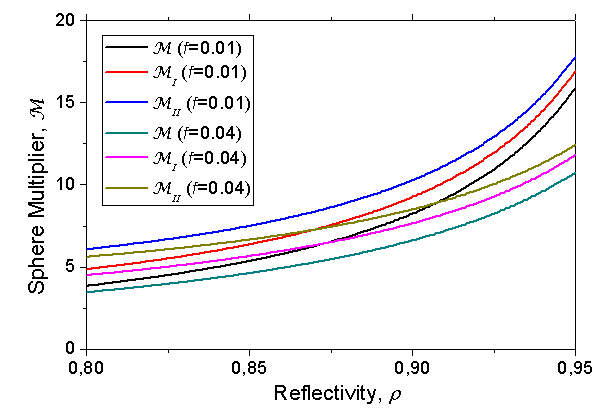 | Figure 5. Sphere multipliers M, MI and MII calculated as function of reflectivity ρ in the 0.8-0.95 interval, for fraction areas f = 0.01 and 0.04 |
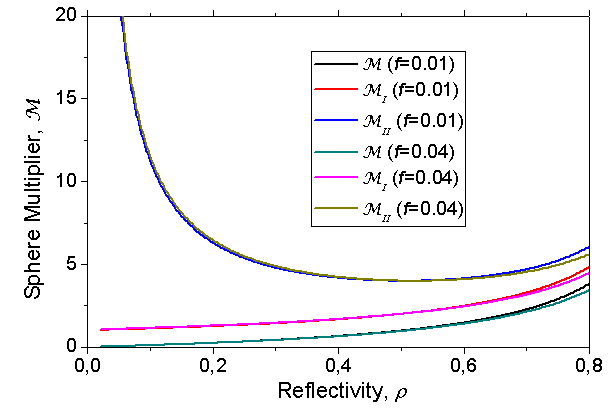 | Figure 6. Sphere multipliers M, MI and MII calculated for wall reflectivity in the 0.0-0.8 interval, for fraction areas f = 0.01 and 0.04 |
4. Conclusions
- In conclusion, we have revisited the common definition of sphere multiplier distinguishing between two types of sphere multipliers, which differ only for the factor ρI. (reflectivity of the first impact region). The two multipliers have been defined considering the following different points of view:i) MI is obtained considering the same flux Φin at input of the planar diffuser and of the integrating sphere;ii) MII is obtained considering a different flux at input, but the same diffused flux at input on the total surface area of the two devices.Differently from the actual theory, moreover, in our theory we have compared an integrating sphere, provided with the different openings for input and output of radiation and for radiation measurements, with a planar diffuser equal to the sphere in that it has been obtained by simply unfolding on a plane the sphere surface. We have finally performed some optical simulations to compare the different definitions of multipliers for a simple geometry of the sphere, in order to highlight the influence of wall reflectivity and fraction area of the windows.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML