1. Introduction

Holography is the science of producing holograms. It is a technique of recording the interference pattern between an object wavefront and a reference wavefront on a holographic medium[1]. Holograms are attractive optical elements that are used in security applications because of their unique property of being difficult to counterfeit. In parallel and real-time processing of objects having various dimensions, holograms are usedfor optical information encryption such as phase, wavelength and polarization.Such an encryption process adds integrity to the stored information and thus serves todeter unauthorized access, copying, or falsification of the authentic products and documents. These parameters of the optical waves have been exploited to realize various optical security systems[2, 3]. Representative examples of these systems include image encryption using random phase encoding, optical pattern recognition, fractional Fourier transform, joint transform correlation, phase only encryption amongst others[3, 4, 5]. The systems are excellent but many of them require accurately fabricated complex masks and fine control of the optical axis alignmentto encode and decode information. They also need specific and costly equipment to decrypt the encrypted information. Apart from these, several simple encoding schemes using holograms have been used. Such schemes have usedanencoded reference beam[6, 7, 8], Moire pattern encoding[9, 10, 11], speckle pattern encoding[12] amongst others for authenticity verification and anti-counterfeit purposes.

There are two methods of acquiring and measuring fringes for the evaluation and testing of optical surfaces and systems. These are static fringe analysis and phase shift analysis. Static fringe analysis employs a framegrabber to digitally capture fringes produced using standard interferometry techniques andsoftware to analyze the fringes. It typically offers an accuracy of around λ/20 and has the benefit that the software results can be verified manually for simple peak to valley measurements[13, 14]. Phase shift analysis can improve accuracy by capturing the fringes with several different phases of the reference beam. This permits calculation of absolute phase for every pixel within the pupil, which increases accuracy and repeatability of measurements to around λ/100. This also allows anyfringe perturbation to be identified as a wavefront retardation or advance. The technique involves using a piezo transducer to move the reference optic by around λ/2 and utilizing dedicated phase shift analysis software to provide full analysis of circular, multiple, low contrast and nulled fringes[13, 15].

The intensity pattern provided by these fringes encodes the physical quantity which is being measured. This intensity varies as the cosine of a phase which is directly proportional to that physical quantity. The processing of the interference fringes allows the extraction of the phase field from one or many intensity fields which have been acquired[14, 15]. The process of phase detection has received considerable attention in the last decade, as video acquisition and computer processing became more powerful and less expensive.

An important issue is the assessment of the relation between the phase and the physical quantity to be measured, when this relation is not linear. This is of particular importance in profilometry[16]. Two main tracks can be followed when determining the phase. Theseare referred to as global and local approaches. In the global approach, often called the Fourier transform technique[16,17, 18] the whole intensity field is processed at the same time. The output phase data depend on the whole set of data in the intensity field. A carrier is necessary so that the phase modulation can be identified in the Fourier domain as the broadening of a well-defined frequency peak. This technique has two main advantages: first, only one intensity field is necessary; that is, one image has to be grabbed and dynamic events can be studied, and second, large phase modulations can be detected by extracting the analytic signal from the intensity field. For metrological applications, the main disadvantage of this technique is that the error on the calculated phase is difficult to evaluate, especially near edges. Another disadvantage is that it is not easy to fully automate, as some filtering in the Fourier plane has to be done that may depend on the pattern to be analyzed. The local approach is called phase-stepping or phase-shifting, and the phase is calculated from local intensity information. Two procedures exist, namely temporal and spatial phase-stepping. In temporal phase- stepping[19, 20, 21], a number of images are taken with a constant and known phase shift δ introduced between successive images. There is no requirement on the fringe pattern, and the calculated phase at a given pixel depends only on the intensities recorded at the same pixel, unless spatial smoothing is used. Obviously, dynamic events cannot be studied as the phase-stepping takes some time. In spatial phase-stepping[22, 23, 24], a carrier is necessary so that a given number N of contiguous pixels sample a period of the intensity signal.

Once fringe patterns have been acquired and evaluation and testing of optical surfaces and systems is done, a set of unique codes are generated from their surface profile. This unique information is used as the input to generate another set of security codes to be used inverifying hologram authenticity. The security codes generated in our case are the barcodes. Abarcode is an optical machine readable representation of data relating to the object to which it is attached. Originally barcodes systematically represented data by varying the widths and spacing of parallel lines, and were referred to as linear or one-dimensional (1D). Later they evolved into rectangles, dots, hexagons and other geometric patterns in two dimensions (2D). Although 2D systems use a variety of symbols, they are generally referred to as barcodes as well. Originally barcodes were scanned by special optical scanners called barcode readers. Later, scanners and interpretive software became available on devices including desktop printers and smartphones[25]. An early use of one type of barcode in an industrial context was sponsored by the Association of American Railroads in the late 1960s. Developed by General Telephone and Electronics (GTE) and called KarTrak ACI (Automatic Car Identification), this scheme involved placing colored stripes in various combinations on steel plates which were affixed to the sides of railroad rolling stock. Two plates were used per car, one on each side, with the arrangement of the colored stripes representing things such as ownership, type of equipment, and identification number[26] The plates were "read" by a trackside scanner located, for instance, at the entrance to a classification yard while the car was moving past[27] The project was abandoned after about ten years because the system proved unreliable after long-term use in the field. Barcodes became commercially successful when they were used to automate supermarket checkout systems, a task for which they have become almost universal. Their use has spread to many other tasks that are generically referred to as automatic identification and data capture (AIDC). The very first scanning of the now ubiquitous Universal Product Code (UPC) barcode was on a pack of Wrigley Company chewing gum in June 1974[28]. The simplicity, universality and low cost of barcodes have limited the role of other systems in the last 40 years after the introduction of the commercial barcode.

2. Recording and Reconstruction of Holograms

To record the holograms the set-up presented in[29] was used. A 35mW linearly polarized Helium Neon Laser of wavelength 632.8 nm was used as a light source. Light from the Laser was spatially filtered using a microscope objective lens of magnification X10 and a 30μm diameter pinholelocated at the focal point of the microscope objective lens.

Before exposing the holographic plate, the set-up was allowed to stabilize for about 120 seconds and the stability of the Laser beam was ensured by monitoring through a spectrum analyser. The holographic plate was ready for processing after exposing it. The processing involved two major processes namely: the developing process and bleaching process. These were carried out in darkness before the film was allowed to dry in the open. The composition of the developer solution included pyrogallic acid, sodium carbonate and ascorbic acid while the bleaching solution used was madefrom potassium dichromate, sulphuric acid and distilled water as discussed in[29].

To replay the hologram, the dry processed holographic plate was placed back in the holder and illuminated using the reference beam only while blocking the object beam as presented in Figure 1. This way the object beam was reconstructed. In order to determine the quality of the hologram images recorded, the diffraction efficiency of each hologram image was measured by determining the power of the first order diffracted beam and the incident beam of the reconstructed wavefront.

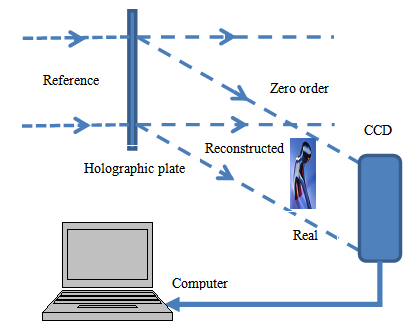Figure 1. Schematic illustration of hologram reconstruction set-up and recording of fringes from reconstructed object wavefront using the CCD camera interfaced to the computer

Different sets of holograms were developed, amongst them being a hologram of two plane waves from the same source. Different objects including a one Kenyan shilling coin, Jomo Kenyatta University of Agriculture and Technology (JKUAT) logo, Kenya Bureau of Standards (KEBS) logo and the Kenyan court of arms logo were used as objects and their respective holograms recorded and developed.

On replaying the hologram by illuminatingthe holographic plate with the original reference beam,the object beam is generated with a characteristic interference pattern detected in the observation plane. It is this generated pattern that was recorded by a CCD camera interfaced with the computer as presented in Figure 1. The recorded patternwas analyzed to give unique information about the incident object. This information is used as an input to generate a set of security codes that can be used for the verification of the hologram authenticity. Different sets of objects were found to give distinctive sets of interference patterns making this a very reliable way of authenticating objects.

An angle of 53⁰ between the reference and object beams was used giving rise to a grating of spatial frequency approximately 1400 lines/mm. The spatial frequency of the holographic plates used was 3000 lines/mm which is much higher than the calculated spatial frequency implying good quality holograms were recorded. This is a very high resolving power in comparison with the photographic films whose resolving power is approximately 200 lines/mm. The holographic image was observed and recorded using a 16.2 Megapixel Kodak digital camera.

3. Results and Discussion

3.1. Analysis of the Fringe Patterns

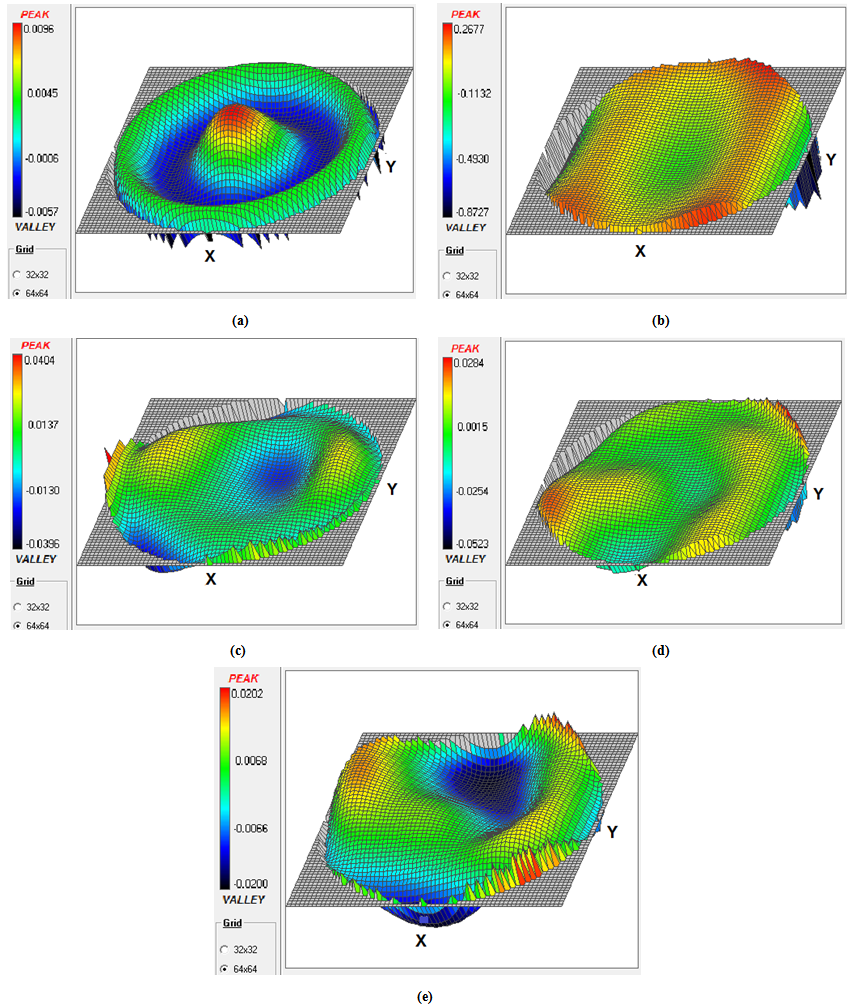
Hologram images were evaluated by measuring their respective diffraction efficiencies. Determination of hologram diffraction efficiency as a function of exposure time was also done. A maximum diffraction efficiency of 21% was achievedwith plane wave holograms. Digital photographs of the objectholograms taken in this research are presented in[29]. The recorded object holograms haddifferent diffraction efficiencies. This was attributed to the difference in surface profile of the objects used. The object with high reflecting surface (The one Shilling Kenyan coin) gave holograms of high diffraction efficiency in comparison with the other objects whose surfaces were dull. Therefore it implies the higher the diffraction efficiency of the hologram the brighter the hologram.

Investigation of the fringes from the holographic plate once illuminated by the reference beam was carried out. Here, a CCD camera was placed on the observation plane behind the holographic plate where the object wavefront was being reconstructed. The fringes on this plane were recorded for each of the objects and are illustrated in Figure 2.

Figure 2. (a) Fringe pattern from the plane wave hologram (b) Fringe pattern from the one shilling Kenyan coin hologram (c) Fringe pattern from the Kenyan coat of arms hologram (d) Fringe pattern obtained from theJomo Kenyatta University of Agriculture and Technology (JKUAT) logo (e) Fringe pattern obtained from the Kenya Bureau of Standards (KEBS) logo hologram

After recording the fringe patterns for the various objects, fringe pattern analysis was done. Using Atmosfringe software[30], three stationery points on the fringe aperture were selectedto mark the portion to be analyzed. A 3D graphical analysis of the wavefront was obtained for each of the hologram fringes and the results are displayed in Figure 3. The plane wave hologram fringes resulted to quite good even profile of the wavefront surface. This is due to the even profile of the collimated object beam used in hologram recording. However, this was not the case for the additional 3D wavefront surface representation of the other object holograms. It is observed that the surface profile of each of thefringe pattern due to the holographically reconstructed wavefront was different. All the incident objects were of different depths and carried different information on their surfaces. This difference, therefore gave rise to the different 3D wavefront surface profile for each of the object holograms as displayed in the figure 3.

Figure 3. 3D graphical analysis of the wavefront surfaceobtained from: (a)Plane wave interference hologram. (b) A one Kenyan shilling coin. (c) The Kenyan Court of Arms. (d) The Jomo Kenyatta University of Agriculture and Technology (JKUAT) logo. (e) The Kenya Bureau of Standards (KEBS) logo hologram

With this set of diverse wavefront patterns obtained, there was need to determine the Modulation transfer function (MTF) of each of the reconstructed object beams. This is one of the most important parameters by which image quality is measured. Optical designers and engineers frequently refer to MTF data, especially in applications where success or failure is contingent on how accurately a particular object is imaged. The MTF of an optical system, as the name implies, is a measurement of its ability to transfer contrast at a particular resolution from the object to the image. Having all the initial conditions constant and no change of the optics in the hologram development setup, implies that the same MTFwas to be obtained if the object beam properties were the same. However, as observed, the MTF curves differed for each of the objects under test. This change in MTF under constant film processing conditions implied that the various objects under test gave out different contrast as a result of their surface profile. Therefore, incident light illuminating these objects was reflected depending on their surface profile and luster. It is this reflected light that was used as the object beam during hologram recording. The object beam therefore carried special information about the surface profile of the object under test.

Figure 4. MTF curve for (a) The plane wave interference hologram. (b) A1 Kenyan shilling coin hologram. (c) The Kenyan Court of Arms hologram. (d) The Jomo Kenyatta University of Agriculture and Technology (JKUAT) logo hologram. (e) The Kenya Bureau of Standards (KEBS) logo hologram

3.2. Error Coding for Security Applications

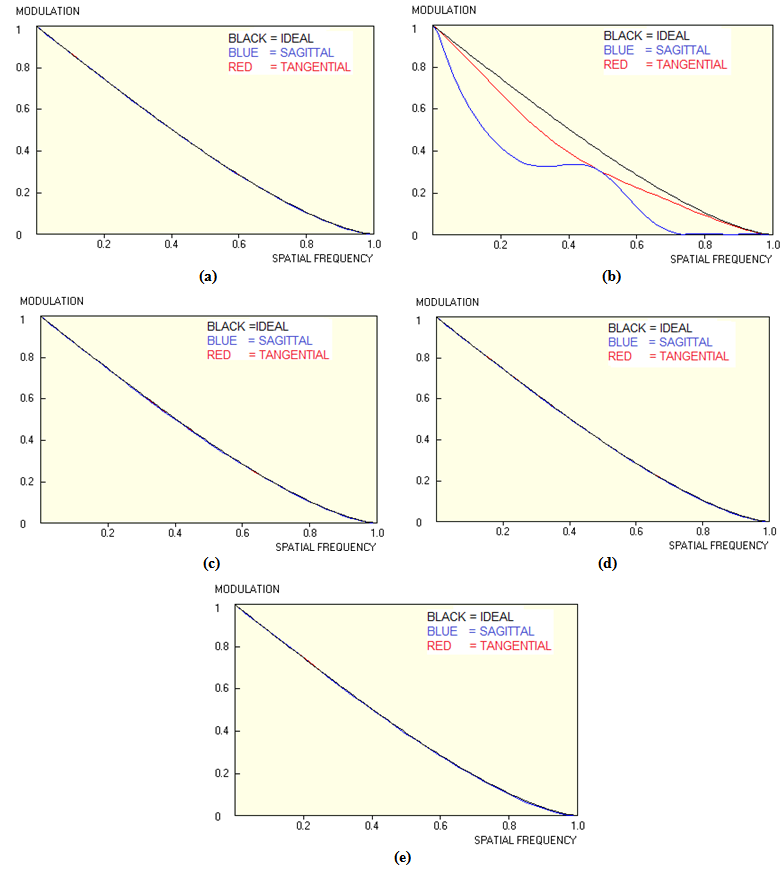
From Figure4, it is clear that even though most ofthe MTF graphs are similar in their shape, they do notmatch exactly onto one another. A closer look at the sagittal and tangential rays shows slight deviations from one set to another, however, Figure 4 (b) gives out very distinctive characteristics of MTF as compared to the rest. This is attributed to the nature of the surface profile of theKenyan one Shilling coin. It has a crown of the court of arms and other information of different depth on the same surface. Its characteristic aluminium luster alsomakes it a good reflector.

With all the above background information, it was important to look for characteristic standards representative of each object hologram. Here, the aberrations of the fringe pattern arising from the holographically reconstructed wavefront; which were very distinctive relative to the objects, were determined. Both the peak to valley, RMS, Strehl ratio, low order Astigmatism, low order Coma and low order Spherical aberrations were measured. It is observed that each object introduced different aberrations on the fringe pattern as confirmed by the different values in Table 1. These characteristic aberration valuesof theobject surface can easily be used as the input to any digital system.The advantage here is that they carry special distinctive information about the surface profile of the hologram already developed.

It is these values that were used as the inputs to the bar code studio software to generate different bar codes for the objects holograms already developed. Different bar codes were generated for the different inputs used. This therefore implied that despite the security hologram obtained, a characteristic bar code was generate dusing the aberrations on the fringes as the input values listed in Table 1. Therefore during authentication process, two things will be verified, the hologram and the bar code values which are representative of the aberrations on the hologram surface. However, special scanners should be designed to read both the hologram and the bar code at the same time, compare the two values and either pass or fail the authentication process. Both the one dimensional linear bar codes and two dimensionaldot codes were generated for the set of hologramsdeveloped.

Table 1. Surface aberration values for the reconstructed object beam for various object holograms ABERRATIONS PLANE WAVE 1 KSH. COIN COURT OF ARMS JKUAT LOGO KEBS LOGO PEAK TO VALLEY 27.7nm 713.9nm 50.1nm 43.8nm 24.4nm RMS 4.1nm 85.6nm 7.7nm 6.0nm 5.5nm STREHL RATIO 0.998 0.485 0.994 0.997 0.997 ASTIGMATISM 5.2nm 263.1nm 19.3nm 8.0nm 16.2nm COMA 11.1nm 46.1nm 16.6nm 3.3nm 16.1nm SPHERICAL 10.5nm -473.7nm -45.9nm -21.2nm 3.2nm

Figure 5. Telepen Alpha linear bar codes for (a) Plane wave interference hologram. (b) One Shilling Kenyancoin hologram. (c) The Kenyan Court of Arms hologram. (d) Jomo Kenyatta University of Agriculture and Technology (JKUAT) logo hologram. (e) Kenya Bureau of Standards (KEBS) logo hologram

Figure 6. 2–D dot codes for (a) Plane wave interference hologram. (b) One Kenyan shilling coin hologram. (c) The Kenyan Court of Arms hologram. (d) Jomo Kenyatta University of Agriculture and Technology (JKUAT) logo hologram. (e) Kenya Bureau of Standards (KEBS) logo hologram

Barcode authentication will involve the examination of scanability as well as the quality of the barcode in comparison to the initial set standards and specifications arising from surface aberration values of the reconstructed hologram. A barcode verifier will be required to perform a series of teststomeasure the barcode optical characteristics relative to the already set standards. This measurement must be repeatable and consistent for any product to pass. For linear barcodes these tests may include: Symbol Contrast, Modulation, Decodability, Edge Determination, Minimum Reflectance and Minimum Edge Contrast while for the 2D dot codes the parameters may include: Symbol Contrast, Modulation, Decodability, Fixed Pattern Damage, Grid Non-uniformity and Axial Non-uniformity. Depending on the parameter, each test is graded and given a pass or fail mark. Each grade is determined by analyzing the scan reflectance profile. Therefore a verifier requires constant conditions such as distance, illumination angle, sensor angle and verifier aperture.

4. Conclusions

A study was carried out to determine whether the fringes formed on the object plane of phase holograms had same properties or not. The experimental results presented in the paper shows that straight line fringes are produced in all the reconstructed object beam images. However, on analysis, the properties of these straight line fringes were found to be different. Each respective object gave out a distinctive reconstructed wavefront surface profile, Modulation Transfer Function and wavefront aberrations. There also exists a relation between the qualities of the hologram images and their respective diffraction efficiency. High diffraction efficiency hologram resulted to bright hologram images. The surface profile of incident object also affects the diffraction efficiencies of holograms under the same processing conditions. Plane wave interference hologram gave the highest diffraction efficiency of 21% while the Court of arms hologram gave a low diffraction efficiency of 13.75%.

From the study, it was found that the reconstructed object beam carried unique information about the incident object. This information was represented inform of surface aberration and Zernike functions. The unique information is encoded and used to generate set of codes that are used as security features on products. Authentic products could feature both the bar code and the hologram. However, special scanners and software would be required for reading and decoding both the hologram and the barcode. On replaying, the special scanner will read both the hologram and the bar code. Decoding the barcode generates the surface aberration values of the said hologram. Similarly, the holographic scanner would read the hologram and the interference pattern on the image plane. This would be decoded via software to generate the aberration on the hologram surface. The two values of aberration would be compared and the system either passes or fails the authentication process of the product.

ACKNOWLEDGEMENTS

The authors appreciate the government of Kenya for funding this project through the National Council of Science and Technology (NCST).