M. A. Morsy1, Hadeel Sami A. Rajab2, Hebah Mohammed Al-Obaidan3
1Electronics and Comm. Eng. Dept., Faculty of Engineering, Ain Shams University, Cairo, Giza, Egypt
2Electrical and Electronics.Dep.,The Higher Institute of Telecommunication And Navigation , PAAET , Kuwait
3Switching .Dep.,The Higher Institute of Telecommunication And Navigation , PAAET , Kuwait
Correspondence to: M. A. Morsy, Electronics and Comm. Eng. Dept., Faculty of Engineering, Ain Shams University, Cairo, Giza, Egypt.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
One of the most important core technologies in the development of optical code division multiple access (OCDMA) local area networks is the optical encoder/decoder embodiment technology which codes information to fixed patterns at the transmitting side and decodes information at the receiving side. The selection of optimized encoding method for network composition is necessary to accommodate a maximum number of subscribers that have simultaneous access over the local area network and the bandwidth of subscriber services available on it. When composing this encoder/decoder optically, passive elements are exclusively used, if possible, so as to make the composition method simple and economical. In this paper we present an analysis of OCDMA passive communication networks focusing on the modeling of optical encoder/decoder blocks for different types of delay elements. The main objective of the paper is to study the performance of these networks including the effect of the passive encoder/decoder parameters such as splitter and optical delay line losses. Different types of delay lines are proposed including optical fibers and fiber Bragg gratings (FBG) as delay elements for the selection of the optical delay line which achieves a better performance. A statistical model of an OCDMA network has been developed and used for this study, including the effect of different passive encoder/decoder parameters, multiple access interference and noise.
Keywords:
Optical Code Division Multiple Access (OCMDA), Fiber Bragg Gratings (FBG), Optical Orthogonal Code(OOC), Optical Delay Lines(ODL)
Cite this paper: M. A. Morsy, Hadeel Sami A. Rajab, Hebah Mohammed Al-Obaidan, Performance of Passive OCDMA Networks for Different Encoder/Decoder Delay Lines, International Journal of Optics and Applications, Vol. 3 No. 3, 2013, pp. 19-26. doi: 10.5923/j.optics.20130303.02.
1. Introduction
The requirements of modern fiber–optic networks bring to the necessity an elaboration of such multiple access algorithms that combine the possibilities of multi–bitrate transmission through a common network, ultra high capacity and all optical processing features to avoid the speed bottleneck of electronic components. A fiber–OCDMA system represents one of the most promising multiple access techniques that respond positively to these needs. Communication systems using CDMA also have the following advantages[1]: 1) Security against unauthorized users,2) Protection against jamming, 3) Flexibility of adding users, and 4) Asynchronous access capability.In an OCDMA system, an optical orthogonal code (OOC) sequence is assigned to each user. A user sends data via the destination user's OOC sequence, which are decoded at the receiving end. There are various design techniques for OOCs that allow many users to access the optical channel simultaneously, provided that their destinations are different. Due to the orthogonality of codes, users of an OCDMA network are able to transmit at overlapping times and wavelengths. The major drawback of an OCDMA system is the length of an OOC which has to be long to support a large number of users. An implementation of these codes is done using optical encoders/decoders employing different arrangements of optical delay elements. The performance of the optical encoder and decoder affects the overall system performance. In the case of real time passive encoder/decoder realization, the encoder or decoder consists of three main elements: a splitter, optical delay elements arrangement and a combiner, each one of whom is defined by several parameters. These parameters affect the performance of the encoder and decoder, hence the overall network performance. To the best of our knowledge, the effect of the optical delay line parameters on the overall system performance has not been thoroughly considered in the published literature. In this paper, OCDMA network performance is evaluated taking into consideration the effect of the optical delay element parameters including its optical transmittivity. Through this work, we have investigated the conventional optical fiber as well as the fiber Bragg gratings as delay elements. Our study shows that the effect of the transmittivity as a main parameter of the delay element on the overall OCDMA system performance is by no means negligible. The use of FBG as delay elements enables the realization of different delays with grating lengths of practically unity transmission and hence provides a better network performance.The paper is organized as follows. In section II, we describe the system architecture. In section III, an overview of optical delay lines of different types is provided. In section IV, we model the encoder/decoder from a photon-counting point of view, taking the transfer characteristics of delay elements into consideration. In section V, the performance analysis results are discussed and finally in section VI, conclusions are drawn.
2. System Description
Figure 1 represents a general configuration for a fiber - OCDMA system, with real time passive encoders/decoders employed in a star topology network. In this network, we assume that there are N active users corresponding to a star coupler with dimensions,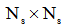 | (1) |
where 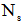 is the maximum number of users allowed on the network. We assign to each user an OOC with length
is the maximum number of users allowed on the network. We assign to each user an OOC with length 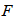 , weight w and minimum auto-correlation
, weight w and minimum auto-correlation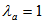 , and cross-correlation
, and cross-correlation 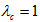 . Therefore, the total number of active users
. Therefore, the total number of active users 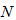 is restricted to[2]:
is restricted to[2]: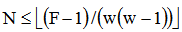 | (2) |
where the symbol 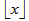 denotes the integer portion of the real value . We also assume that all users transmit binary data at an equal rate and with a period
denotes the integer portion of the real value . We also assume that all users transmit binary data at an equal rate and with a period 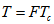 in a continuous fashion, where
in a continuous fashion, where 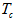 is the chip time of a given OOC. On-off signaling is used such that at the beginning of each frame (consisting of F slots), the source generates a Poisson – distributed pulse with duration
is the chip time of a given OOC. On-off signaling is used such that at the beginning of each frame (consisting of F slots), the source generates a Poisson – distributed pulse with duration 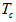 and with a mean number of photons
and with a mean number of photons 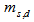 , where
, where 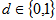 denotes the data bit, assuming
denotes the data bit, assuming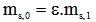 | (3) |
where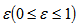 is the source extinction ratio. Thus, each frame consists of
is the source extinction ratio. Thus, each frame consists of 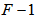 background pulses each with mean
background pulses each with mean 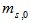 and one original data pulse with mean
and one original data pulse with mean 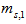 . Several types of optical delay lines are proposed for use in the real time passive encoder/decoder of the fiber - OCDMA network and we compare between them from a BER performance point of view. We employ an optical preamplifier with gain
. Several types of optical delay lines are proposed for use in the real time passive encoder/decoder of the fiber - OCDMA network and we compare between them from a BER performance point of view. We employ an optical preamplifier with gain 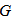 , noise factor
, noise factor 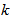 given by[2]:
given by[2]: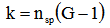 | (4) |
where 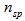 is the spontaneous emission parameter of the preamplifier and amplified spontaneous emission parameter
is the spontaneous emission parameter of the preamplifier and amplified spontaneous emission parameter 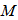 . For our analysis, we use a p-i-n photodetector with quantum efficiency
. For our analysis, we use a p-i-n photodetector with quantum efficiency 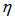 and to simplify calculations, we neglect its dark current. The electric bandwidth is assumed to be wide enough to accept a pulse with duration
and to simplify calculations, we neglect its dark current. The electric bandwidth is assumed to be wide enough to accept a pulse with duration 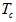 . We assume an integrate and dump receiver with integration time
. We assume an integrate and dump receiver with integration time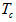 . Thermal noise is modeled as a Gaussian random variable with zero mean and a variance defined as:
. Thermal noise is modeled as a Gaussian random variable with zero mean and a variance defined as: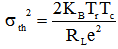 | (5) |
where 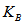 is Boltzman's constant,
is Boltzman's constant, 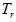 is the receiver noise temperature,
is the receiver noise temperature,  is the receiver load resistance and is the electronic charge.
is the receiver load resistance and is the electronic charge. 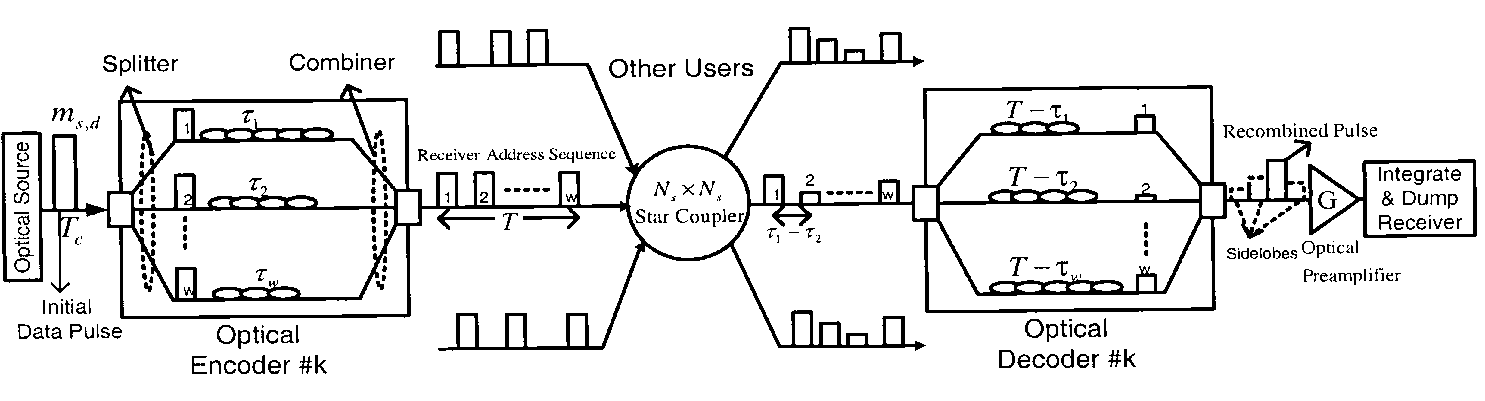 | Figure 1. The fiber-OCDMA system using real time passive encoders/decoders and optical preamplifiers |
3. Optical Delay Lines
Optical delay lines provide a time delay for an optical signal and have been considered important in several different contexts. In optical time division multiple access communication systems, the function of these delay lines is required for synchronization purposes. In optical code division communication systems, this function is required for encoding and decoding the optical data pulses. Figure 2 show two physical implementations of optical delay lines. The simplest implementation of a delay line is to introduce a physical distance, such as a length of optical fiber or free space as shown in figure 2 (a). In this case, the group delay is simply 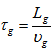 where
where 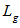 is the physical length of the propagation medium and the group velocity in the medium is:
is the physical length of the propagation medium and the group velocity in the medium is: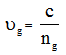 | (6) |
where 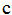 is the speed of light in vacuum, and
is the speed of light in vacuum, and 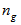 is the medium group index.Although simple, this implementation suffers from two drawbacks:1) significant tunability is difficult to be achieved and 2) long time-delays (
is the medium group index.Although simple, this implementation suffers from two drawbacks:1) significant tunability is difficult to be achieved and 2) long time-delays (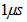 ) requires
) requires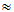 200 meters of optical fiber, which now affects the delay line transmittivity.
200 meters of optical fiber, which now affects the delay line transmittivity.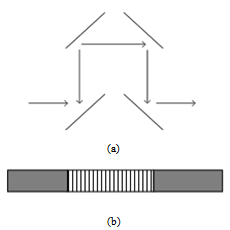 | Figure 2. Two physical implementations of an optical delay line: a) free space, and b) FBG |
Based on these observations, it seems worthwhile to define a figure of merit that characterizes the size of the group delay relative to the size of the device; the group index 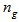 can serve as this figure of merit, where from (6), we have
can serve as this figure of merit, where from (6), we have 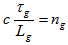 . A large figure of merit implies large delay in a small device. An alternative approach to generate a time delay is to employ resonant enhancement in one of two ways:1) enhancing the physical length,
. A large figure of merit implies large delay in a small device. An alternative approach to generate a time delay is to employ resonant enhancement in one of two ways:1) enhancing the physical length, 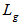 , by forcing the light to traverse the physical distance many times, for example using a ring resonator.2) utilizing a material resonance, where the dispersion is large and
, by forcing the light to traverse the physical distance many times, for example using a ring resonator.2) utilizing a material resonance, where the dispersion is large and 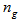 may accordingly become large, thus making
may accordingly become large, thus making 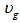 small, as in the case of using fiber Bragg gratings[3]. In both cases, the result is a much smaller device, which is easier to manipulate and therefore tune. A fiber Bragg grating is shown in figure 2 (b), which acts as an optical filter because of the existence of a stop band, the frequency region in which most of the incident light is reflected back. The stop band is centered at the Bragg wavelength
small, as in the case of using fiber Bragg gratings[3]. In both cases, the result is a much smaller device, which is easier to manipulate and therefore tune. A fiber Bragg grating is shown in figure 2 (b), which acts as an optical filter because of the existence of a stop band, the frequency region in which most of the incident light is reflected back. The stop band is centered at the Bragg wavelength 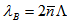 , where
, where 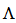 is the grating period and
is the grating period and 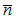 is the average mode index. Two possible types of fiber Bragg gratings are: 1) uniform period grating, and 2) chirped fiber grating. For a uniform grating the refractive index along the length varies periodically as:
is the average mode index. Two possible types of fiber Bragg gratings are: 1) uniform period grating, and 2) chirped fiber grating. For a uniform grating the refractive index along the length varies periodically as: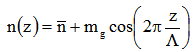 | (7) |
where 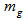 is the modulation depth (typically around
is the modulation depth (typically around 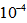 ) and the transfer function of the grating, is given by:
) and the transfer function of the grating, is given by: 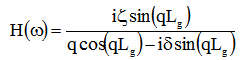 | (8) |
where 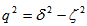 ,
,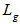 is the grating length,
is the grating length, 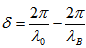 is the detuning from the Bragg wavelength,
is the detuning from the Bragg wavelength, 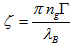 is the coupling coefficient, and
is the coupling coefficient, and 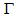 is the confinement factor. Figure 3 shows the reflectivity
is the confinement factor. Figure 3 shows the reflectivity 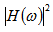 and transmittivity
and transmittivity 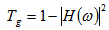 for
for 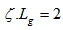 . We can use the uniform grating in the region with
. We can use the uniform grating in the region with 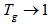 . As shown in figure 4, this can be satisfied for different values of
. As shown in figure 4, this can be satisfied for different values of 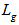 at constant coupling coefficient and detuning value, but is not satisfied in the optical fiber, where the transmission coefficient decreases with increasing fiber length. The chirped fiber grating has a nonlinear transmittivity outside the stop band. Accordingly, this type can not be used as a delay element.
at constant coupling coefficient and detuning value, but is not satisfied in the optical fiber, where the transmission coefficient decreases with increasing fiber length. The chirped fiber grating has a nonlinear transmittivity outside the stop band. Accordingly, this type can not be used as a delay element.
4. Encoder /Decoder Modelling
4.1. Encoder Model
Figure 5 shows the real time passive encoder consisting of optical splitter, optical delay lines and optical combiner. The encoder output moment generating function (MGF) is[2]: 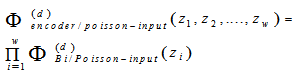 | (9) |
Where 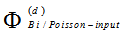 is the MGF of the output code sequence due to the original data pulse and the extinction power pulses at the input of the encoder. This MGF is affected by the encoder parameters such that,
is the MGF of the output code sequence due to the original data pulse and the extinction power pulses at the input of the encoder. This MGF is affected by the encoder parameters such that,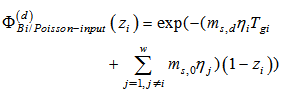 | (10) |
where 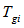 is the transmittivity of the delay line in branch number
is the transmittivity of the delay line in branch number 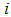 , and
, and 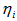 the splitting parameter in the same branch.In this model we use uniform FBG as optical delay lines in the transmission mode. This gives the required delayed chips of the code sequence by the same number of photons, or by the same amplitude levels. For uniform gratings, the time delay is given by:
the splitting parameter in the same branch.In this model we use uniform FBG as optical delay lines in the transmission mode. This gives the required delayed chips of the code sequence by the same number of photons, or by the same amplitude levels. For uniform gratings, the time delay is given by: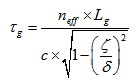 | (11) |
If 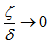 , which is a condition for
, which is a condition for 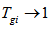 and in the case of all output pulses with the same amplitude, this gives at the end of the encoder:
and in the case of all output pulses with the same amplitude, this gives at the end of the encoder: 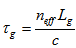 | (12) |
then the maximum time delay is: 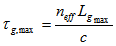 | (13) |
and the minimum time delay is: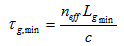 | (14) |
thus 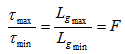 | (15) |
then the code length is limited by the ratio between maximum and minimum lengths of the uniform grating (note that 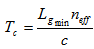 ), and the minimum length of the uniform grating is limited by the chip time. If we need to increase the code length this requires:1) optical source with very small chip time in the order of sub-picoseconds,2) Photodetector with high bandwidth, and sufficiently fast modulation technique.
), and the minimum length of the uniform grating is limited by the chip time. If we need to increase the code length this requires:1) optical source with very small chip time in the order of sub-picoseconds,2) Photodetector with high bandwidth, and sufficiently fast modulation technique.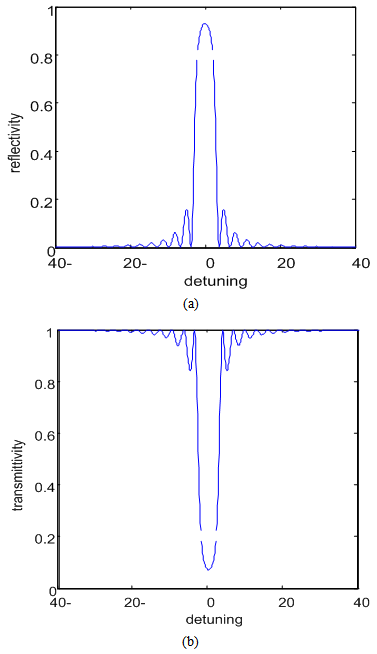 | Figure 3. a) The reflectivity, and b) the transmittivity, of the FBG at 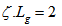 |
4.2. Decoder Model
Figure 6 shows a real time passive decoder used for fiber OCDMA. According to this figure, the output MGF of the decoder can be simplified to: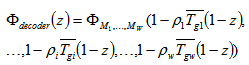 | (16) |
where 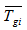 is the complement transmittivity of the branch i of the optical delay line in the encoder and
is the complement transmittivity of the branch i of the optical delay line in the encoder and 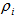 is the splitting parameter in branch i of the decoder.The total MGF of the system due to the desired user and the interfering users is:
is the splitting parameter in branch i of the decoder.The total MGF of the system due to the desired user and the interfering users is: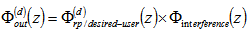 | (17) |
where  is the MGF of the recombined pulse of the desired user. In fiber OCDMA we consider a user to be interfering whenever its interference data
is the MGF of the recombined pulse of the desired user. In fiber OCDMA we consider a user to be interfering whenever its interference data 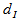 is equal to 1, in this way; the accumulated interference due to all other users in the network can be written as follows:
is equal to 1, in this way; the accumulated interference due to all other users in the network can be written as follows:
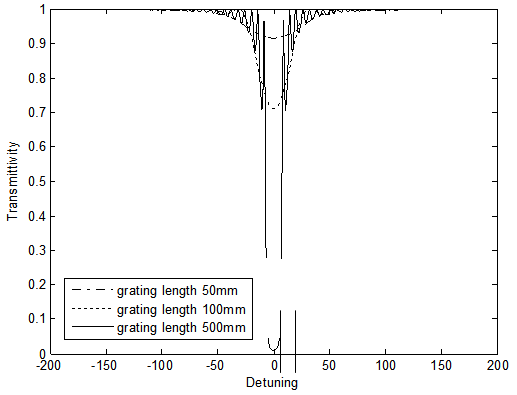 | Figure 4. The FBG transmittivity versus detuning at different values of the grating length |
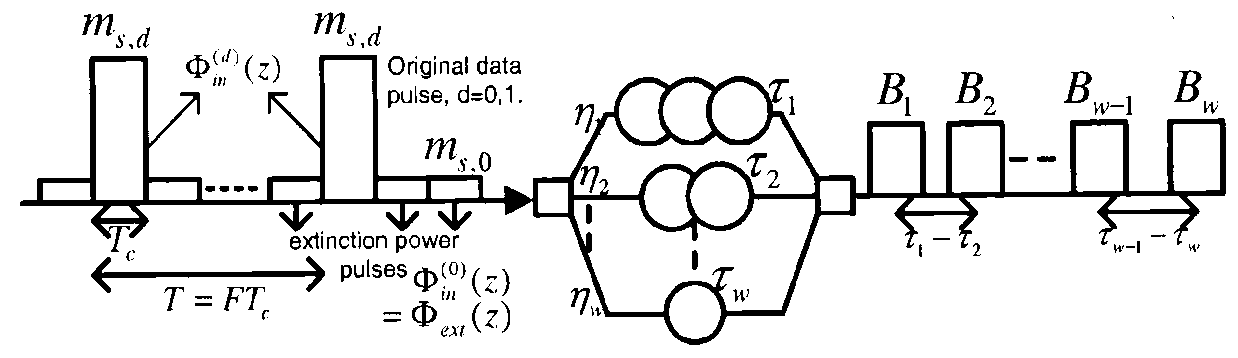 | Figure 5. The real time passive encoder used for fiber – OCDMA |
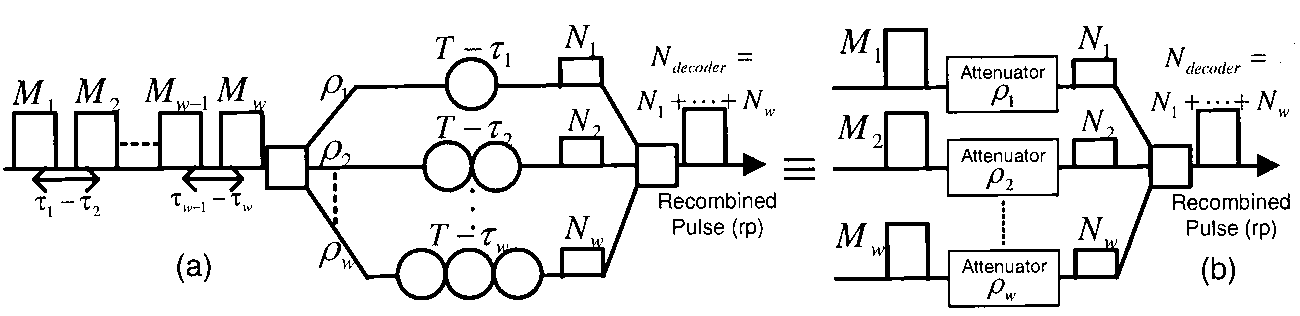 | Figure 6. The real time passive decoder used for fiber – OCDMA and its equivalent model |
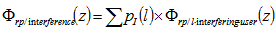 | (18) |
where 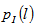 is the probability distribution of the interfering users and
is the probability distribution of the interfering users and 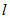 is their number. It is noted that,
is their number. It is noted that,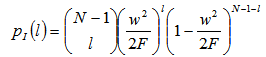 | (19) |
Then we have 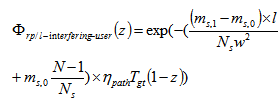 | (20) |
assuming that 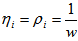 , and the star coupler splitting parameter is
, and the star coupler splitting parameter is 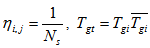 .The path loss coefficient is
.The path loss coefficient is 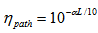 , where L is the fiber length from the source to detector in km, and
, where L is the fiber length from the source to detector in km, and 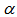 is the fiber attenuation coefficient in dB/km. The desired user MGF due to the original data pulse and the background pulses is eventually given as:
is the fiber attenuation coefficient in dB/km. The desired user MGF due to the original data pulse and the background pulses is eventually given as: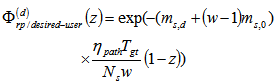 | (21) |
5. Encoder Performance Evaluation and Numerical Results
In this section, we evaluate the performance of the system using the improved Gaussian approximation method; the exact calculation of the probability of error 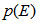 is given by:
is given by: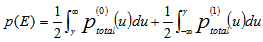 | (22) |
where 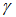 is the chosen threshold and we assume equiprobable data transmission.
is the chosen threshold and we assume equiprobable data transmission. 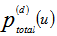 is the PDF of the random variable (RV):
is the PDF of the random variable (RV): 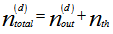 where
where 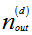 is the output count of the photodetector, and
is the output count of the photodetector, and 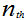 is the Gaussian thermal noise RV. We then have[4]:
is the Gaussian thermal noise RV. We then have[4]: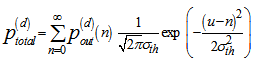 | (23) |
Where,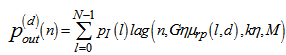 | (24) |
and lag( ) is the laguerre distribution. The computation of 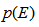 using (22) is very complicated. Its Gaussian approximation form is given by[2]:
using (22) is very complicated. Its Gaussian approximation form is given by[2]: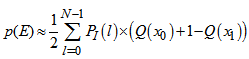 | (25) |
where 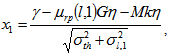 | (26) |
and 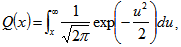 , with
, with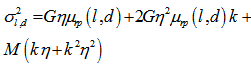 | (27) |
and 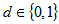 is the variance of the corresponding random variable of the laguerre distribution:
is the variance of the corresponding random variable of the laguerre distribution: 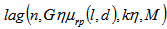 , where
, where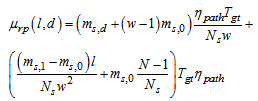 | (28) |
is the mean number of photons in the recombined pulse in the presence of 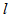 interfering users. Figure 7 shows the system performance in terms of BER versus the transmitted mean number of photons for different code lengths. The calculations have been done for two types of optical delay elements; the conventional optical fibers and the fiber Bragg gratings with different transmittivities. Thermal noise power has been taken into consideration using an optical preamplifier with adaptive gain and integrate and dump receiver with adaptive threshold[5], assuming 100km of fiber with attenuation coefficient 0.2dB/km at an operating wavelength of 1.55 microns. As figure 7 shows, the performance is improved as the mean number of photons
interfering users. Figure 7 shows the system performance in terms of BER versus the transmitted mean number of photons for different code lengths. The calculations have been done for two types of optical delay elements; the conventional optical fibers and the fiber Bragg gratings with different transmittivities. Thermal noise power has been taken into consideration using an optical preamplifier with adaptive gain and integrate and dump receiver with adaptive threshold[5], assuming 100km of fiber with attenuation coefficient 0.2dB/km at an operating wavelength of 1.55 microns. As figure 7 shows, the performance is improved as the mean number of photons 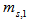 increases to a certain value. The performance is almost constant as
increases to a certain value. The performance is almost constant as 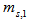 exceeds this value. The results show that, this value of transmitted power depends on the code weight and code length and the FBG outperforms the optical fiber delay line. The system performance enhancement when optical fiber delay line is replaced by FBG increases as the code length F increases. Figure 8 shows the system performance in terms of BER versus the number of simultaneous active users N using optical fibers and FBGs as optical delay elements. From figure 8 it is seen that FBG delay elements perform better than optical fiber delay lines for different transmittivities and for different code lengths. The superiority of using FBGs over optical fiber delay lines is due to the presence of insertion loss when using optical fibers due to the fiber attenuation over the long fiber lengths needed, while by adjusting FBGs their insertion loss can be almost zero. This loss increases with the code length F. Also the transmittivity of the FBG can be taken as unity irrespective of the code length F whereas the transmittivity of optical fiber delay lines decreases with increasing code length F.
exceeds this value. The results show that, this value of transmitted power depends on the code weight and code length and the FBG outperforms the optical fiber delay line. The system performance enhancement when optical fiber delay line is replaced by FBG increases as the code length F increases. Figure 8 shows the system performance in terms of BER versus the number of simultaneous active users N using optical fibers and FBGs as optical delay elements. From figure 8 it is seen that FBG delay elements perform better than optical fiber delay lines for different transmittivities and for different code lengths. The superiority of using FBGs over optical fiber delay lines is due to the presence of insertion loss when using optical fibers due to the fiber attenuation over the long fiber lengths needed, while by adjusting FBGs their insertion loss can be almost zero. This loss increases with the code length F. Also the transmittivity of the FBG can be taken as unity irrespective of the code length F whereas the transmittivity of optical fiber delay lines decreases with increasing code length F. 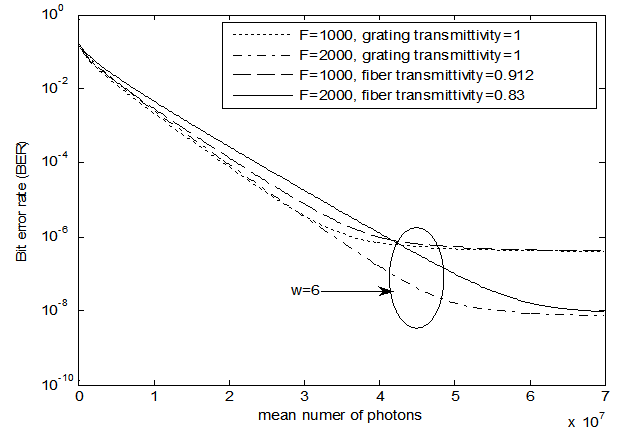 | Figure 7. The system performance versus mean number of photons at different transmittivity of delay elements |
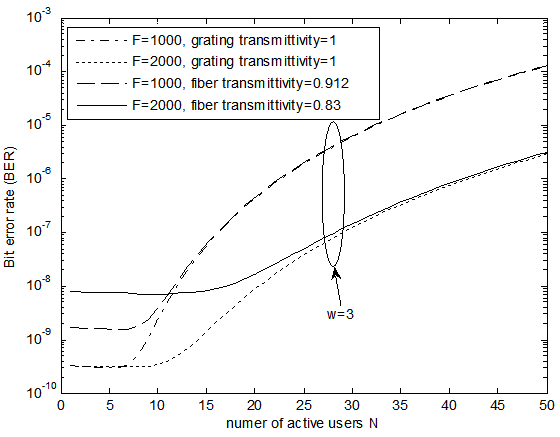 | Figure 8. The system performance versus the number of active users at different transmittivity of the delay elements |
6. Conclusions
The In this paper, the fiber-OCDMA system using real time passive encoders/decoders is analyzed using fiber Bragg gratings in transmission mode at high detuning, as delay elements. In this case, the code sequence can be obtained with the same chip amplitudes at the output of the encoder. This system has been compared to the system using conventional optical fibers as delay elements. The high detuning of fiber Bragg gratings gives the same transmittivity for all grating lengths used in a typical system, in contrast to the case of optical fiber delay elements where different values of attenuation are obtained in the code sequence at the output of the encoder. This is also a problem when using optical amplifiers before the star coupler, and after the light source[6-19]. As the code length F increases the transmittivity of optical fiber delay lines decreases which degrades the BER performance of the network. For FBG delay lines, a near ideal transmittivity is obtained, achieving better performance. From the results obtained herein, it can be concluded that at low transmitted power and when the number of active users is less than a certain threshold, which in our simulations was around 25, the system using FBG outperforms that using optical fibers as delay elements.
References
| [1] | C. Argon, and S. W. McLaughlin, “Optical OOK – CDMA and PPM – CDMA Systems with Turbo Product Codes,” J. Lightwave Technol., Vol. 20, pp. 1653 – 1663, Sept. 2002. |
| [2] | M. Razavi, and J. A. Salehi, “Statistical Analysis of Fiber – Optic CDMA Communication Systems – Part I: Device Modeling,” J. Lightwave Technol., Vol. 20, pp. 1304 – 1316, Aug. 2002. |
| [3] | G. Lenz, B. J. Eggleton, C. K. Madsen, and R. E. Slusher, “Optical Delay Lines Based on Optical Filters,” J. Quantum Electronics, Vol. 37, pp. 525 – 532, April 2001. |
| [4] | J. A. Salehi, and C. A. Brackett, “Code Division Multiple – Access Techniques in Optical Fiber Networks – part II: System Performance Analysis,” IEEE Trans. Comm., Vol. 37, pp. 834 – 842, Aug. 1989. |
| [5] | R. F. Ormondroyd, and M. M. Mustapha, “Optically Orthogonal CDMA System Performance with Optical Amplifier and Photodetector Noise,” IEEE Photonic Technol. Lett., Vol. 11, pp. 617 – 619, May 1999. |
| [6] | M. Razavi, and J. A. Salehi, “Statistical Analysis of Fiber – Optic CDMA Communication Systems – Part II: Incorporating Multiple Optical Amplifiers,” J. Lightwave Technol., Vol. 20, pp. 1317 – 1334, Aug. 2002. |
| [7] | Z. Wei and H. Ghafouri-Shiraz, Proposal of a novel code for spectral amplitude coding optical CDMA systems. IEEE Photonics Tech. Letters, 2002. vol. 14(no. 3): p. 414-416. |
| [8] | M. M. N. Hamarsheh, H. M. H. Shalaby, and M. K. Abdullah, Design and analysis of dynamic code division multiple access communication system based on tunable optical filter. J. Lightw. Technol., 2005. vol. 23(no. 12): p. 3959-3965. |
| [9] | M. Y. Liu and H. W. Tsao, Cochannel interference cancellation via employing a reference correlator for synchronous optical CDMA system. J. Microw. & Opt. Technol. Letteres, 2000. vol. 25(no. 6): p. 390-392. |
| [10] | U. N. Griner and S. Arnon, A novel bipolar wavelength-time coding scheme for optical CDMA systems. IEEE Photonics Tech. Letters, 2004. vol. 16(no. 1): p. 332- 334. |
| [11] | F. Gu and J. Wu, Construction of two-dimensional wavelength/time optical orthogonal codes using difference family. J. Lightw. Technol., 2005. vol. 23(no. 11): p. 3642-3652. |
| [12] | F. R. K. Chung, J. A. Salehi, and V. K. Wei, Optical orthogonal codes: design, analysis and application. IEEE Trans. on Info. Theory, 1989. vol. 35(no. 3): p. 595-605. Lightwave Technol. Vol. 17, pp. 1284 – 1293, August 1999. |
| [13] | L. L. Jau and Y. H. Lee, Optical code-division multiplexing systems using Manchester coded Walsch codes. IEE Optoelectronics, 2004. vol. 151(no. 2): p. 81-86. |
| [14] | F. Liu, Estimation of new-modified prime code in synchronous incoherent CDMA network, in MPhil Dissertation at School of EECE. 2006, University of Birmingham. |
| [15] | S. V. Maric, New family of algebraically designed optical orthogonal codes for use in CDMA fiber optic networks. Eletronics Letters, 1993. vol. 29(no. 6): p. 538 539. |
| [16] | C. S. Weng and J. Wu, Perferct difference codes for synchronous fiber-optic CDMA communication systems. J. Lightw. Technol., 2001. vol. 19(no. 2): p. 186- 194. |
| [17] | G. C. Yang and W. C. Kwong, Performance analysis of optical CDMA with prime codes. Eletronics Letters, 1995. vol. 31(no. 7): p. 569-570. |
| [18] | J. G. Zhang and W. C. Kwong, Design of optical code-division multiple-access networks with modified prime codes. Eletronics Letters, 1997. vol. 33(no. 3): p. 229-230. |
| [19] | F. Liu and H. Ghafouri-Shiraz. Analysis of PPM-CDMA and OPPM-CDMA communication systems with new optical code. in Proc. of SPIE. 2005. |
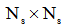
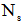 is the maximum number of users allowed on the network. We assign to each user an OOC with length
is the maximum number of users allowed on the network. We assign to each user an OOC with length 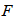 , weight w and minimum auto-correlation
, weight w and minimum auto-correlation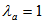 , and cross-correlation
, and cross-correlation 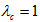 . Therefore, the total number of active users
. Therefore, the total number of active users 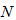 is restricted to[2]:
is restricted to[2]: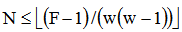
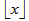 denotes the integer portion of the real value . We also assume that all users transmit binary data at an equal rate and with a period
denotes the integer portion of the real value . We also assume that all users transmit binary data at an equal rate and with a period 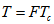 in a continuous fashion, where
in a continuous fashion, where 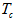 is the chip time of a given OOC. On-off signaling is used such that at the beginning of each frame (consisting of F slots), the source generates a Poisson – distributed pulse with duration
is the chip time of a given OOC. On-off signaling is used such that at the beginning of each frame (consisting of F slots), the source generates a Poisson – distributed pulse with duration 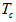 and with a mean number of photons
and with a mean number of photons 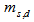 , where
, where 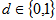 denotes the data bit, assuming
denotes the data bit, assuming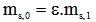
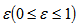 is the source extinction ratio. Thus, each frame consists of
is the source extinction ratio. Thus, each frame consists of 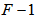 background pulses each with mean
background pulses each with mean 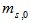 and one original data pulse with mean
and one original data pulse with mean 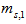 . Several types of optical delay lines are proposed for use in the real time passive encoder/decoder of the fiber - OCDMA network and we compare between them from a BER performance point of view. We employ an optical preamplifier with gain
. Several types of optical delay lines are proposed for use in the real time passive encoder/decoder of the fiber - OCDMA network and we compare between them from a BER performance point of view. We employ an optical preamplifier with gain 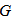 , noise factor
, noise factor 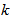 given by[2]:
given by[2]: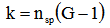
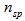 is the spontaneous emission parameter of the preamplifier and amplified spontaneous emission parameter
is the spontaneous emission parameter of the preamplifier and amplified spontaneous emission parameter 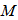 . For our analysis, we use a p-i-n photodetector with quantum efficiency
. For our analysis, we use a p-i-n photodetector with quantum efficiency 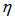 and to simplify calculations, we neglect its dark current. The electric bandwidth is assumed to be wide enough to accept a pulse with duration
and to simplify calculations, we neglect its dark current. The electric bandwidth is assumed to be wide enough to accept a pulse with duration 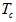 . We assume an integrate and dump receiver with integration time
. We assume an integrate and dump receiver with integration time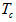 . Thermal noise is modeled as a Gaussian random variable with zero mean and a variance defined as:
. Thermal noise is modeled as a Gaussian random variable with zero mean and a variance defined as: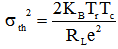
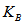 is Boltzman's constant,
is Boltzman's constant, 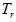 is the receiver noise temperature,
is the receiver noise temperature,  is the receiver load resistance and is the electronic charge.
is the receiver load resistance and is the electronic charge. 
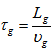 where
where 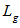 is the physical length of the propagation medium and the group velocity in the medium is:
is the physical length of the propagation medium and the group velocity in the medium is: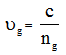
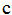 is the speed of light in vacuum, and
is the speed of light in vacuum, and 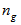 is the medium group index.Although simple, this implementation suffers from two drawbacks:1) significant tunability is difficult to be achieved and 2) long time-delays (
is the medium group index.Although simple, this implementation suffers from two drawbacks:1) significant tunability is difficult to be achieved and 2) long time-delays (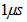 ) requires
) requires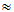 200 meters of optical fiber, which now affects the delay line transmittivity.
200 meters of optical fiber, which now affects the delay line transmittivity.
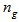 can serve as this figure of merit, where from (6), we have
can serve as this figure of merit, where from (6), we have 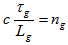 . A large figure of merit implies large delay in a small device. An alternative approach to generate a time delay is to employ resonant enhancement in one of two ways:1) enhancing the physical length,
. A large figure of merit implies large delay in a small device. An alternative approach to generate a time delay is to employ resonant enhancement in one of two ways:1) enhancing the physical length, 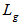 , by forcing the light to traverse the physical distance many times, for example using a ring resonator.2) utilizing a material resonance, where the dispersion is large and
, by forcing the light to traverse the physical distance many times, for example using a ring resonator.2) utilizing a material resonance, where the dispersion is large and 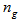 may accordingly become large, thus making
may accordingly become large, thus making 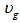 small, as in the case of using fiber Bragg gratings[3]. In both cases, the result is a much smaller device, which is easier to manipulate and therefore tune. A fiber Bragg grating is shown in figure 2 (b), which acts as an optical filter because of the existence of a stop band, the frequency region in which most of the incident light is reflected back. The stop band is centered at the Bragg wavelength
small, as in the case of using fiber Bragg gratings[3]. In both cases, the result is a much smaller device, which is easier to manipulate and therefore tune. A fiber Bragg grating is shown in figure 2 (b), which acts as an optical filter because of the existence of a stop band, the frequency region in which most of the incident light is reflected back. The stop band is centered at the Bragg wavelength 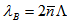 , where
, where 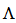 is the grating period and
is the grating period and 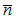 is the average mode index. Two possible types of fiber Bragg gratings are: 1) uniform period grating, and 2) chirped fiber grating. For a uniform grating the refractive index along the length varies periodically as:
is the average mode index. Two possible types of fiber Bragg gratings are: 1) uniform period grating, and 2) chirped fiber grating. For a uniform grating the refractive index along the length varies periodically as: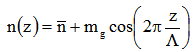
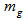 is the modulation depth (typically around
is the modulation depth (typically around 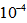 ) and the transfer function of the grating, is given by:
) and the transfer function of the grating, is given by: 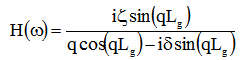
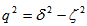 ,
,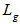 is the grating length,
is the grating length, 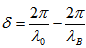 is the detuning from the Bragg wavelength,
is the detuning from the Bragg wavelength, 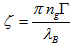 is the coupling coefficient, and
is the coupling coefficient, and 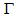 is the confinement factor. Figure 3 shows the reflectivity
is the confinement factor. Figure 3 shows the reflectivity 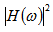 and transmittivity
and transmittivity 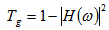 for
for 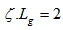 . We can use the uniform grating in the region with
. We can use the uniform grating in the region with 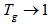 . As shown in figure 4, this can be satisfied for different values of
. As shown in figure 4, this can be satisfied for different values of 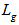 at constant coupling coefficient and detuning value, but is not satisfied in the optical fiber, where the transmission coefficient decreases with increasing fiber length. The chirped fiber grating has a nonlinear transmittivity outside the stop band. Accordingly, this type can not be used as a delay element.
at constant coupling coefficient and detuning value, but is not satisfied in the optical fiber, where the transmission coefficient decreases with increasing fiber length. The chirped fiber grating has a nonlinear transmittivity outside the stop band. Accordingly, this type can not be used as a delay element.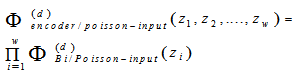
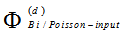 is the MGF of the output code sequence due to the original data pulse and the extinction power pulses at the input of the encoder. This MGF is affected by the encoder parameters such that,
is the MGF of the output code sequence due to the original data pulse and the extinction power pulses at the input of the encoder. This MGF is affected by the encoder parameters such that,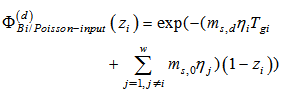
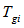 is the transmittivity of the delay line in branch number
is the transmittivity of the delay line in branch number 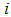 , and
, and 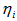 the splitting parameter in the same branch.In this model we use uniform FBG as optical delay lines in the transmission mode. This gives the required delayed chips of the code sequence by the same number of photons, or by the same amplitude levels. For uniform gratings, the time delay is given by:
the splitting parameter in the same branch.In this model we use uniform FBG as optical delay lines in the transmission mode. This gives the required delayed chips of the code sequence by the same number of photons, or by the same amplitude levels. For uniform gratings, the time delay is given by: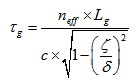
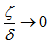 , which is a condition for
, which is a condition for 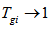 and in the case of all output pulses with the same amplitude, this gives at the end of the encoder:
and in the case of all output pulses with the same amplitude, this gives at the end of the encoder: 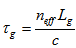
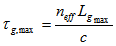
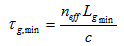
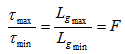
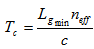 ), and the minimum length of the uniform grating is limited by the chip time. If we need to increase the code length this requires:1) optical source with very small chip time in the order of sub-picoseconds,2) Photodetector with high bandwidth, and sufficiently fast modulation technique.
), and the minimum length of the uniform grating is limited by the chip time. If we need to increase the code length this requires:1) optical source with very small chip time in the order of sub-picoseconds,2) Photodetector with high bandwidth, and sufficiently fast modulation technique.
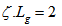
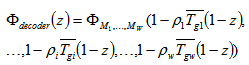
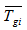 is the complement transmittivity of the branch i of the optical delay line in the encoder and
is the complement transmittivity of the branch i of the optical delay line in the encoder and 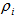 is the splitting parameter in branch i of the decoder.The total MGF of the system due to the desired user and the interfering users is:
is the splitting parameter in branch i of the decoder.The total MGF of the system due to the desired user and the interfering users is: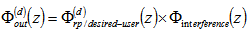
 is the MGF of the recombined pulse of the desired user. In fiber OCDMA we consider a user to be interfering whenever its interference data
is the MGF of the recombined pulse of the desired user. In fiber OCDMA we consider a user to be interfering whenever its interference data 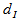 is equal to 1, in this way; the accumulated interference due to all other users in the network can be written as follows:
is equal to 1, in this way; the accumulated interference due to all other users in the network can be written as follows:


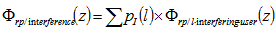
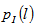 is the probability distribution of the interfering users and
is the probability distribution of the interfering users and 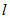 is their number. It is noted that,
is their number. It is noted that,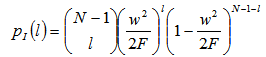
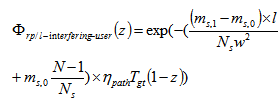
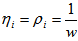 , and the star coupler splitting parameter is
, and the star coupler splitting parameter is 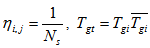 .The path loss coefficient is
.The path loss coefficient is 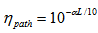 , where L is the fiber length from the source to detector in km, and
, where L is the fiber length from the source to detector in km, and 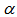 is the fiber attenuation coefficient in dB/km. The desired user MGF due to the original data pulse and the background pulses is eventually given as:
is the fiber attenuation coefficient in dB/km. The desired user MGF due to the original data pulse and the background pulses is eventually given as: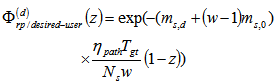
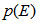 is given by:
is given by: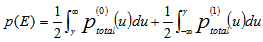
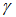 is the chosen threshold and we assume equiprobable data transmission.
is the chosen threshold and we assume equiprobable data transmission. 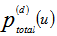 is the PDF of the random variable (RV):
is the PDF of the random variable (RV): 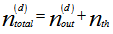 where
where 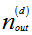 is the output count of the photodetector, and
is the output count of the photodetector, and 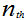 is the Gaussian thermal noise RV. We then have[4]:
is the Gaussian thermal noise RV. We then have[4]: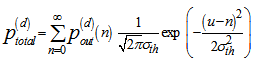
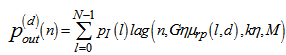
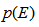 using (22) is very complicated. Its Gaussian approximation form is given by[2]:
using (22) is very complicated. Its Gaussian approximation form is given by[2]: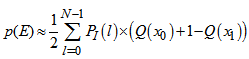
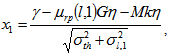
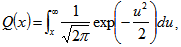 , with
, with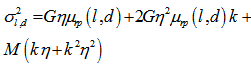
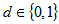 is the variance of the corresponding random variable of the laguerre distribution:
is the variance of the corresponding random variable of the laguerre distribution: 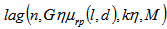 , where
, where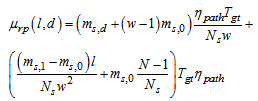
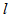 interfering users. Figure 7 shows the system performance in terms of BER versus the transmitted mean number of photons for different code lengths. The calculations have been done for two types of optical delay elements; the conventional optical fibers and the fiber Bragg gratings with different transmittivities. Thermal noise power has been taken into consideration using an optical preamplifier with adaptive gain and integrate and dump receiver with adaptive threshold[5], assuming 100km of fiber with attenuation coefficient 0.2dB/km at an operating wavelength of 1.55 microns. As figure 7 shows, the performance is improved as the mean number of photons
interfering users. Figure 7 shows the system performance in terms of BER versus the transmitted mean number of photons for different code lengths. The calculations have been done for two types of optical delay elements; the conventional optical fibers and the fiber Bragg gratings with different transmittivities. Thermal noise power has been taken into consideration using an optical preamplifier with adaptive gain and integrate and dump receiver with adaptive threshold[5], assuming 100km of fiber with attenuation coefficient 0.2dB/km at an operating wavelength of 1.55 microns. As figure 7 shows, the performance is improved as the mean number of photons 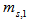 increases to a certain value. The performance is almost constant as
increases to a certain value. The performance is almost constant as 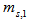 exceeds this value. The results show that, this value of transmitted power depends on the code weight and code length and the FBG outperforms the optical fiber delay line. The system performance enhancement when optical fiber delay line is replaced by FBG increases as the code length F increases. Figure 8 shows the system performance in terms of BER versus the number of simultaneous active users N using optical fibers and FBGs as optical delay elements. From figure 8 it is seen that FBG delay elements perform better than optical fiber delay lines for different transmittivities and for different code lengths. The superiority of using FBGs over optical fiber delay lines is due to the presence of insertion loss when using optical fibers due to the fiber attenuation over the long fiber lengths needed, while by adjusting FBGs their insertion loss can be almost zero. This loss increases with the code length F. Also the transmittivity of the FBG can be taken as unity irrespective of the code length F whereas the transmittivity of optical fiber delay lines decreases with increasing code length F.
exceeds this value. The results show that, this value of transmitted power depends on the code weight and code length and the FBG outperforms the optical fiber delay line. The system performance enhancement when optical fiber delay line is replaced by FBG increases as the code length F increases. Figure 8 shows the system performance in terms of BER versus the number of simultaneous active users N using optical fibers and FBGs as optical delay elements. From figure 8 it is seen that FBG delay elements perform better than optical fiber delay lines for different transmittivities and for different code lengths. The superiority of using FBGs over optical fiber delay lines is due to the presence of insertion loss when using optical fibers due to the fiber attenuation over the long fiber lengths needed, while by adjusting FBGs their insertion loss can be almost zero. This loss increases with the code length F. Also the transmittivity of the FBG can be taken as unity irrespective of the code length F whereas the transmittivity of optical fiber delay lines decreases with increasing code length F. 

 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML