-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Optics and Applications
2012; 2(3): 29-33
doi: 10.5923/j.optics.20120203.03
Squeezing Interferometry for Optical Phase Extraction in Digital Speckle Pattern Interferometry
Vamara Dembele, Khalid Assid, Faiçal Alaoui, Abdel Karim Nassim
Laboratoire Instrumentation de Mesure et de Contrôle, Equipe Metrologie Optique et Traitement, Image, Université Chouaib
Correspondence to: Khalid Assid, Laboratoire Instrumentation de Mesure et de Contrôle, Equipe Metrologie Optique et Traitement, Image, Université Chouaib.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
The purpose of the present work is the use of squeezing interferometry Technique to provide an optical phase mapping from DSPI fringes. The main advantage of this technique is to demodulate by means of a quadrature Gabor filter, a single carrier-frequency fringe pattern formed from intermixing M shifted fringe patterns that are synthetised numerically by the combination of a primary interferogram and its quadrature, which leads directly to the phase without any speckle denoising algorithm, and this after unwrapping the phase with a standard phase unwrapping algorithm and using a simple median filter to smooth the result. This approach was tested on simulated interferograms for different speckle sizes and fringes densities; it was found that the procedure was able to give the result with a good accuracy for all these cases. An application of the proposed procedure to retrieve the phase for experimental fringes recorded from the thermomechanical study of the MOS power transistor is also presented.
Keywords: Speckle Interferometry, Squeezing Interferometry, Phase Shifting, Phase Unwrapping
Article Outline
1. Introduction
- Digital speckle pattern interferometry (DSPI) is a whole field optical method for non- contact and nondestructive surface analysis. It’s now considered as a powerful tool for industrial measurements. It enables full-field measurement of optical phase changes via the acquisition of speckle patterns[1-3]. After acquisition, a simple subtraction is usually performed to obtain a correlation fringe pattern. The greatest challenges in speckle interferometry focus on relating fringe patterns to phase mapping, permitting the direct determination of surface deformation. However, as DSPI fringes are characterized by a strong speckle noise background, a denoising method[4-6] must be used before the phase evaluation. The development of more sophisticated phase evaluation algorithms such as Phase Shifting methods, are continuously needed[7-9].The phase shifting technique is the most used in many areas of precise metrology. It ensures a maximum accuracy of the calculated phase, providing quantitative information from interferograms. The phase-shifting technique requires a sequence of interferograms shifted in phase. Usually a minimum of three phase-shifted images is needed. There are many techniques available in the literature for phase shifting interferometry. Malacara, et. al.,[10] has an exhaustive amount of phase shifting algorithms.The aim of this paper is to use the Squeezing interferometry Technique[11] to retrieve a phase mapping from only two π/2 shifted speckle fringe patterns without any speckle denoising filtring. The principle of squeezing interferometry is based on transforming N phase shifted fringe patterns by a blending technique into a single carrier fringe pattern and then demodulating this carrier interferogram with a Gabor filter[12]. After unwrapping the result by a special phase unwrapping algorithm named PUMA[13], then we applied a median filter to smooth the unwrapped phase.The paper is organized as follows. In section 2, we present a brief description of Digital Speckle Pattern Interferometry (DSPI) technique, the Squeezing interferometry Technique and our procedure to provide the phase mapping. In section 3, we present different results on simulated speckle fringe patterns and experimental interferograms acquired from the real fringes of an MOS power transistor to perform the method. Finally, a conclusion is given in section 4.
2. Squeezing Interferometry Technique In Digital Speckle Pattern Interferometry
2.1. Speckle Fringe Correlation
- The speckle fringe patterns are obtained by subtraction of a reference speckled image from the image of a displaced surface. The intensity distribution of a reference speckled image (before displacement) is
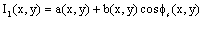 | (1) |
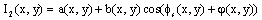 | (2) |
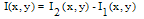 | (3) |
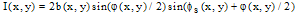 | (4) |
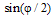 fringe term (shape of envelope modulating the random speckle term) may be rectified and filtered by appropriate computer image processing in order to remove the high frequency
fringe term (shape of envelope modulating the random speckle term) may be rectified and filtered by appropriate computer image processing in order to remove the high frequency 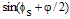 noise.Squaring Eq. (4) leads to
noise.Squaring Eq. (4) leads to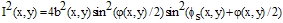 | (5) |
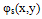 changes rapidly across the speckle pattern, the ensemble average of the second sine squared term in Eq. (5) across the whole measurement area leads to
changes rapidly across the speckle pattern, the ensemble average of the second sine squared term in Eq. (5) across the whole measurement area leads to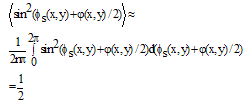 | (6) |
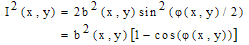 | (7) |
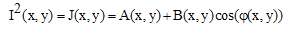 | (8) |
2.2. Synthetic Shifted Fringe Patterns
- The major phase-shifting techniques require a sequence of shifted interferograms by adding progressively a known phase step. Usually a minimum of three phase-shifted interferograms are needed. In our work, we will generate numerically multiple interferograms with arbitrary phase-shift amount between them from only two interferograms shifted by π/2.
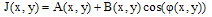 | (9) |
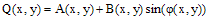 | (10) |
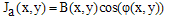 | (11) |
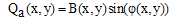 | (12) |
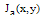 and its quadrature
and its quadrature 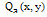 with cos(β) and sin(β) respectively which leads to the β shifted fringe pattern.
with cos(β) and sin(β) respectively which leads to the β shifted fringe pattern.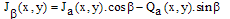 | (13) |
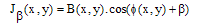 | (14) |
2.3. Squeezing Interferometry Technique
- The principle of squeezing interferometry[11] is based on transforming M temporal-spatial phase shifted fringe patterns by a blending technique into a single carrier fringe pattern and then demodulating this carrier interferogram to retrieve the phase.Squeezing interferometry rearranges the data of M frames of phase shifted interferograms with size LxL to a spatial linear carrier interferogram with extended size MLxL, which converts the temporal phase shift to the spatial carrier.A sequence of M phase shifted interferograms can be written as
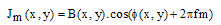 | (15) |
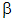 is
is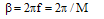 Squeezing interferometry rearranges the data of the M interferograms[11] to obtain the frequency carrier interferogram by
Squeezing interferometry rearranges the data of the M interferograms[11] to obtain the frequency carrier interferogram by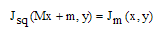 | (16) |
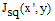 . The fringe pattern representation of this re-arrangement is defined by
. The fringe pattern representation of this re-arrangement is defined by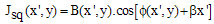 | (17) |
2.4. Gabor Filter Demodulation
- The carrier frequency interferogram can be demodulated using the Gabor filter[12] described as
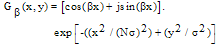 | (18) |
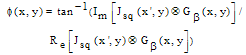 | (19) |
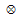 denotes convolution;
denotes convolution;  is the retrieved phase, and the operators
is the retrieved phase, and the operators 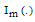 and
and 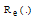 are the imaginary and real parts of the two-dimensional convolution product
are the imaginary and real parts of the two-dimensional convolution product 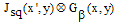 .
.3. Numerical Results
3.1. DSPI Phase Retrieval Without Speckle Interferogram Denoising
- The presentation given in the previous section is a generalization for M shifted interferograms with a phase step of
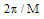 . As our method enables generation of multiple interferograms with arbitrary phase shifts, we will limit our study to 3 frames shifted with
. As our method enables generation of multiple interferograms with arbitrary phase shifts, we will limit our study to 3 frames shifted with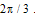 .From Eq. (13), we generated the three fringe patterns with the phase step
.From Eq. (13), we generated the three fringe patterns with the phase step 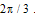 according to the following formulas
according to the following formulas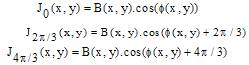 | (20) |
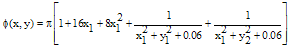 | (21) |
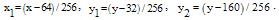 To evaluate the accuracy of this technique, we adopted the fidelity measure f[13] which is defined by
To evaluate the accuracy of this technique, we adopted the fidelity measure f[13] which is defined by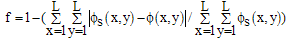 | (22) |
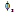 represents the synthetised phase,
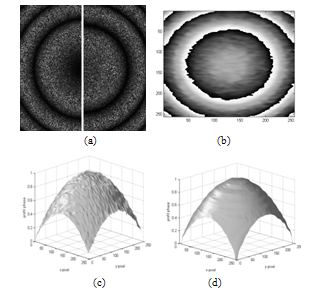
represents the synthetised phase, 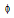 is the retrieved phase. The fidelity quantifies how well the details are preserved in the retrieved image. Desirable values for f are close to 1.The interferogram and its quadrature are shown in Fig.1. In Fig.2, we show the three synthesized 2π/3 shifted interferograms.
is the retrieved phase. The fidelity quantifies how well the details are preserved in the retrieved image. Desirable values for f are close to 1.The interferogram and its quadrature are shown in Fig.1. In Fig.2, we show the three synthesized 2π/3 shifted interferograms. | Figure 1. Panel (a) is the cosine interferogram. Panel (b) is the sine interferogram |
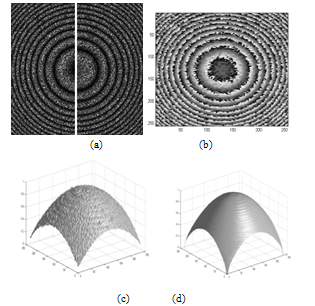
 | Figure 2. Three synthesized interferograms shifted by 2π/3 In Fig.3, the spatial-carrier frequency interferogram blended from the three synthesized fringe patterns is shown. |
 | Figure 3. Single image spatial-carrier frequency interferogram |
 | Figure 4. Wrapped Phase distribution obtained from Gabor filter |
3.2. Effect of the Speckle Size
- To emphazise the speckle size effect on this technique, we conducted a series of DSPI simulations for different average speckle sizes. The following phase distribution was simulated
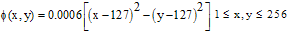 | (23) |
|
3.3. Effect of the fringe density
- To emphazise the fringe density effect on this technique, we conducted a series of DSPI simulations for different fringe densities and an average speckle size of 1 pixels. The results are presented in table 2. These results show that our procedure continues to give very good results even in the case of high density fringes.
3.4. Experimental results
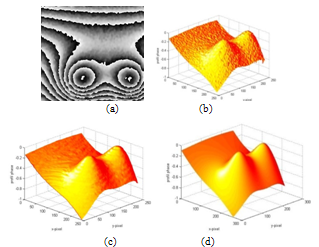
- The reliability of power devices depends strongly on their working temperature and the related thermal dilatation. To perform the method, we have used two π/2 shifted fringe patterns obtained from the MOS transistor thermomechanical deformation experiment. This study allows determining displacement components of points of the surface of an active MOS transistor in thermal equilibrium and the transient deformation of the out-of-plane deformation.
 | Figure 8. Thermomechanical study of transistor, (a) the primary interferogram, (b) the quadrature interferogram |
 | Figure 9. Frequency carrier fringe pattern obtained from the 2π/3 shifted fringe patterns |
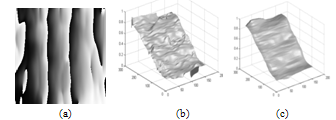 | Figure 10. Retrieved phase by squeezing interferometry technique for the CMOS transistor. (a) wrapped phase, (b) unwrapped phase, (c) smoothed phase |
5. Conclusions
- In this paper, we have presented and tested a squeezing interferometry technique for phase extraction from two π/2 shifted interferograms. We have introduced digitally the three 2π/3 shifted fringes patterns, and applied the blending technique; we generate a single spatial-carrier frequency interferogram using a two dimensional quadrature Gabor filter. After unwrapping the result by the PUMA algorithm, we applied a simple median filter to smooth the phase. We have obtained the phase distribution with a good accuracy avoiding the complex step of speckle denoising. We performed our results on a thermomechanical MOS transistor deformation experiment, where the phase map was easily obtained.
ACKNOWLEDGEMENTS
- We want to thank Dr Joseph W. Goodman for his constructive and helpful comments.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML