-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Optics and Applications
2012; 2(3): 20-28
doi: 10.5923/j.optics.20120203.02
Tuning of Wavelengths for Producing Eye Safe Laser Using Second Order Nonlinear Processes
1Applied Science Department, GB Pant Engineering College, Pauri (Garhwal), Uttarakhand, India
2Department of Physics, HNB Garhwal University Srinagar (Garhwal), Uttarakhand, India
Correspondence to: Kireet Semwal, Applied Science Department, GB Pant Engineering College, Pauri (Garhwal), Uttarakhand, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
We are introducing here conversion of eye hazardous laser to the eye safe region by Optical Parametric Oscillation (OPO) method, using nonlinear optical crystals. The practical optical parametric oscillator device consists of a nonlinear crystal enclosed in an optical resonant cavity pumped by Nd:YAG laser. Optical parametric devices generate broadly tunable coherent optical radiations by the phase-matching nonlinear optical interaction of an intense laser beam with this nonlinear crystal. In this process the high energy pump photon is converted into a pair of lower frequency signal and idler photons while conserving the total energy and momentum. Tunability of the signal-idler pair is usually achieved by changing the crystal birefringence of the angular dependence of the extraordinary index of the nonlinear crystal. The output energy is an eye safe radiation at either, or both the signal and idler wavelengths.
Keywords: Optical parametric oscillation (OPO), nonlinear optics, Phase Matching, Eye safe Laser
Article Outline
1. Introduction
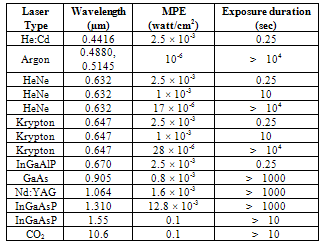
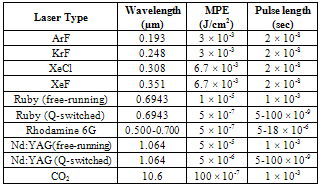
- Laser application have proliferate in recent years and, as to be expected, their presence is no longer confined to the laboratory or places where access to their radiation can be controlled. One obvious application where this is so, is Military operations where various devices such as laser range finders, target designators, and secure communications equipment elevate the risk of exposure, specifically eye exposure, to unacceptable levels. Although the need for eye protection in the laboratory and other controlled areas has been appreciated since the invention of the laser, the use of lasers in circumstances where safety or the risk of loss of vision, has made adequate eye protection essential. It is found that laser with operating wavelengths in the region of approximately 0.4 µm to 1.4 µm (i.e. visible and near infrared) is the eye hazardous portion of optical spectrum, because in this region it is transmitted by the cornea and the lens serves to focus the laser beam on the retina. Thus, the actual laser power density entering the eye can be increased by some 105 by the time the light gets to the retina, and burn it without any time lag. This hazardous wavelength region often called ocular focus region [1]. Whereas wavelengths beyond this region are absorbed in the cornea, lens, and vitreous humor of eye, and therefore laser cannot make direct impact on the retina. In this region our eye is relatively safe, and there is only thermal injury to eye. Therefore retinal damage is often more severe than corneal damage.Eye damage may not only result from laser light coming directly from the laser, but may also by light coming from secondary light path i.e. reflection, refraction, scattering etc. For extremely high-power laser, even diffuse reflections may be capable of causing eye damage [2] [3].
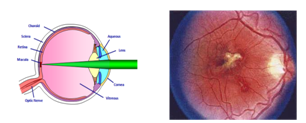 | Figure 1. Construction of eye and eye injury by laser |
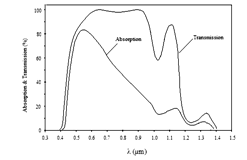 | Figure 2. Eye transmission and absorption |
|
|
2. Second Order Nonlinear Processes:
- In the regime of conventional optics, the electric polarization vector P is simply assumed to be linearly proportional to the electric field strength E of an applied optical wave, i.e.
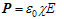 | (1) |
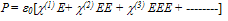 | (2) |
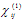 is a second – rank (linear) tensor (9 components xx, xy, xz, yx,……..), where
is a second – rank (linear) tensor (9 components xx, xy, xz, yx,……..), where 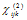 is a third -rank (nonlinear) tensor (27 components, xxx, xxy, xxz, xyx,…….), and
is a third -rank (nonlinear) tensor (27 components, xxx, xxy, xxz, xyx,…….), and 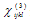 is a forth-rank (nonlinear) tensor (81 components, xxxx,xxxy, xxxz, xxyx,……). The values of the tensor coefficients are functions of frequency and temperature. The subscripts m, n, and o etc. denotes different frequency components, and i, j, k and l are Cartesian indices that run from 1 to 3. For small field strength the polarization is proportional to the electric field E and is accounted for by the polarizatbility tensor
is a forth-rank (nonlinear) tensor (81 components, xxxx,xxxy, xxxz, xxyx,……). The values of the tensor coefficients are functions of frequency and temperature. The subscripts m, n, and o etc. denotes different frequency components, and i, j, k and l are Cartesian indices that run from 1 to 3. For small field strength the polarization is proportional to the electric field E and is accounted for by the polarizatbility tensor 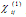 . All of the optics discussed so far has been linear optics encompassed in the term
. All of the optics discussed so far has been linear optics encompassed in the term 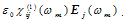 . This term represents optical phenomenon that are proportional to the electric field and are at the frequency of incoming wave [1][6].The term
. This term represents optical phenomenon that are proportional to the electric field and are at the frequency of incoming wave [1][6].The term 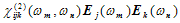 is responsible for all of the two-wave effects. This includes second harmonic generation (two fields at ω to make one at 2ω) and parametric oscillation (one field at ω1 and other field at ω2 to create fields at ω1 - ω2 and ω1 + ω2). This also includes optical mixing, and the Pocals effect (change of index of refraction with applied electric field). The nonlinear polarization tensor
is responsible for all of the two-wave effects. This includes second harmonic generation (two fields at ω to make one at 2ω) and parametric oscillation (one field at ω1 and other field at ω2 to create fields at ω1 - ω2 and ω1 + ω2). This also includes optical mixing, and the Pocals effect (change of index of refraction with applied electric field). The nonlinear polarization tensor 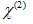 vanishes in the crystals that have a center of symmetry (i.e. crystal symmetry). In these crystals second harmonic generation is not possible. As a result of, many of the components of
vanishes in the crystals that have a center of symmetry (i.e. crystal symmetry). In these crystals second harmonic generation is not possible. As a result of, many of the components of 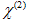 will be zero or equal to other components of the tensor. Thus the second-order polarization and the corresponding monochromatic components of the optical field:
will be zero or equal to other components of the tensor. Thus the second-order polarization and the corresponding monochromatic components of the optical field: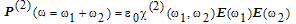 (3)where
(3)where 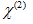 denotes the second-order susceptibility that is a third-order tensor. Desmond [7] simplified
denotes the second-order susceptibility that is a third-order tensor. Desmond [7] simplified 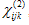 , and replaced by a nonlinear optical coefficient dil (Coulomb/Volt2), according to the following relationship:
, and replaced by a nonlinear optical coefficient dil (Coulomb/Volt2), according to the following relationship: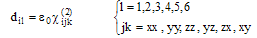 | (4) |
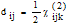 , here,ε0, is the permittivity of free space, some authors excludes ε0 from the d coefficient, in this case d [As/V2] = 8.855 10-12 d [m/v]. The conversion from the cgs system to MKS units becomes d [As/V2] = 3.68 10-15 d [esu]. In most practical situations the tensor equations containing dijk can be simplified to non-tensor form in which dijk is replaced by deff, is the effective nonlinear coefficient for the interaction dependent on crystal symmetry and propagation direction in the medium.
, here,ε0, is the permittivity of free space, some authors excludes ε0 from the d coefficient, in this case d [As/V2] = 8.855 10-12 d [m/v]. The conversion from the cgs system to MKS units becomes d [As/V2] = 3.68 10-15 d [esu]. In most practical situations the tensor equations containing dijk can be simplified to non-tensor form in which dijk is replaced by deff, is the effective nonlinear coefficient for the interaction dependent on crystal symmetry and propagation direction in the medium.2.1. Second Harmonic Generation:
- The simplest second-order process is that of second-harmonic generation (SHG). In this process, an intense laser beam of angular frequency ω1 (= ω) is passed through a crystal having nonzero value of
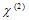 , such that the beam emerging from the crystal contains the angular frequencies ω1 of the input beam and also ω2 = 2ω1, twice the frequency of the input beam. This can be shown to occur by considering the second order nonlinear polarization term
, such that the beam emerging from the crystal contains the angular frequencies ω1 of the input beam and also ω2 = 2ω1, twice the frequency of the input beam. This can be shown to occur by considering the second order nonlinear polarization term 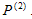 . Under certain conditions (like phase matching), it is possible to covert nearly all of the original frequency of the beam to the second harmonic frequency. Thus, second harmonic generation is a
. Under certain conditions (like phase matching), it is possible to covert nearly all of the original frequency of the beam to the second harmonic frequency. Thus, second harmonic generation is a 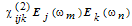 process where a wave at frequency ω is converted into one at frequency 2ω. The second-order nonlinear effects can occur in the non-centrosymmetrical crystals only [8]. In the dielectric dipole approximation, isotropic media and centrosymmetrical crystals cannot be used to generate second-order nonlinear effects. Therefore, the media for SHG should be the crystals having no inversion symmetry. This requirement is the same as that for the piezoelectric effect; thus all SHG crystals are piezoelectric crystals although the physical mechanisms for these two effects are not related to each other.
process where a wave at frequency ω is converted into one at frequency 2ω. The second-order nonlinear effects can occur in the non-centrosymmetrical crystals only [8]. In the dielectric dipole approximation, isotropic media and centrosymmetrical crystals cannot be used to generate second-order nonlinear effects. Therefore, the media for SHG should be the crystals having no inversion symmetry. This requirement is the same as that for the piezoelectric effect; thus all SHG crystals are piezoelectric crystals although the physical mechanisms for these two effects are not related to each other.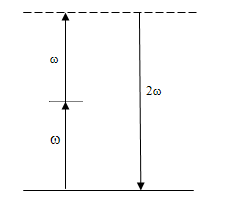 | Figure 3. Second harmonic generation |
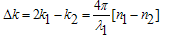 | (5) |
2.2. Optical Sum, Difference Frequency Generation & Optical Parametric Oscillation
- In the second-harmonic generation, considered the combination (addition) of two photons of the same frequency to produce a single photon of twice the frequency. It can now to generalize this process to allow for the case in which the two photons have different frequencies ω1 and ω2. These include second harmonic terms (involving 2ω1 and 2ω2), and two new terms involving ω1 + ω2 and ω1 - ω2. The new term involving ω1 + ω2 generates a new frequency that is the sum of the two original frequencies and is thus known as sum frequency generation. The term involving the difference between the two frequencies, ω1 - ω2 , is referred to as difference frequency generation. In the process of difference frequency mixing, the frequency ω2 is amplified while the frequency ω3 is being generated. In the process of optical parametric oscillation (OPO) the intense input laser beam at frequency ωp is known as the pump frequency, when passes through a nonlinear material, generates the desired frequencies ωs (signal frequency) and the frequency ωi (idler frequency) [13] shown in Figure-4.
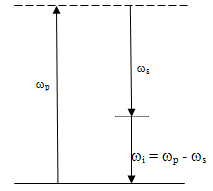 | Figure 4. Optical parametric oscillation |
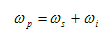 | (6) |
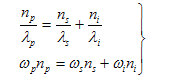 | (7) |
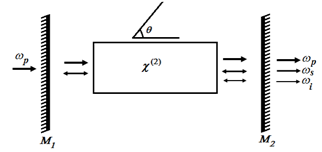 | Figure 5. Singly-Resonant Optical Parametric Oscillator |
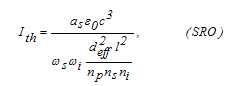 | (8) |
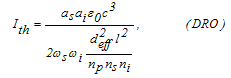 | (9) |
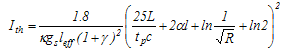 | (10) |
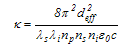 | (11) |
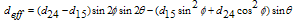 | (12) |
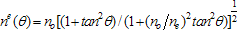 | (13) |
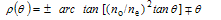 | (14) |
2.3. Nonlinear Optical Materials
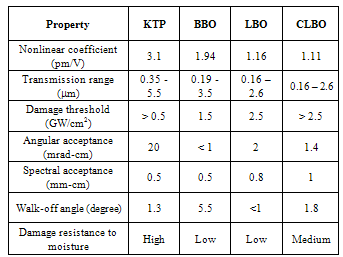
- For generating new frequencies from existing lasers via harmonic generation and difference generation, they must (1) be resistant to optical damage, (2) have high mechanical hardness, (3) exhibit good thermal and chemical stability, (4) be capable of being grown in useful sizes, and (5) have the appropriate phase-matching properties. The second harmonic crystals must have no inversion symmetry (i.e. non-centrosymmetric). Bulk second-order nonlinear materials are generally inorganic crystals. A number of semiconductors are useful for second harmonic generation when used in waveguides. The nonlinear crystals can be classified into two groups according to their physical properties. Crystals grown from water solutions are fragile, hygroscopic, and sensitive to thermal shock. The crystals of this group, to which KDP and its isomorphs belong, are somewhat difficult to handle because the crystals are soft, and the polished faces may be fogged if they are held with bare hands or exposed to humid atmosphere. On the other hand, the crystals are easy to grow, they are available in large sizes, and they are of excellent optical quality. Crystals grown from the melt are relatively hard, nonhygroscopic and less sensitive to thermal shock. Important members of this group crystals are LiNbO3 (LBO) , Ba2NaNb5O15 (BBO) and KTiOPO4 (KTP). KTP possesses good optical properties, a large acceptance angle, large temperature acceptance, a large nonlinear coefficient, and high optical damage thresholds [16][23][28][29].
|
3. Result & Discussion
- The active laser medium consists of an antireflection-coated Nd:YAG laser rod transverse pumped by laser diode arrays. Two diode laser bars of total power 12 W transversely pumps, a 40 mm long, 5 mm diameter Nd:YAG laser rod. The diode-laser array has maximum pulse width 100 ms, repetition rate 50 Hz with a total input of 120 mJ at 808 nm from the two transverse laser diodes. Up to, 40 mJ TEM00 mode energy is obtained by Nd:YAG at 1064 nm. The 42 cm long laser cavity is formed by two Plano concave confocal mirrors, with 5 m radius of curvature. The rear mirror M1 is 100 % reflective dielectric coated for wavelength at 1064 nm whereas output coupler M2 is having 70 % reflective coating at 1064 nm. The bandwidth of laser spectra is 0.2 nm. The TEM00, mode is obtained by keeping an aperture in front of mirror M2.
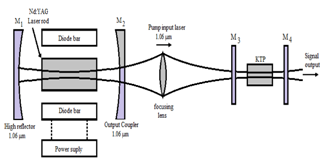 | Figure 6. Schematic diagram for the Nd:YAG eye safe laser system |
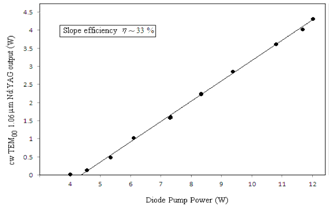 | Figure 7. Output characteristics of the single transverse mode laser |
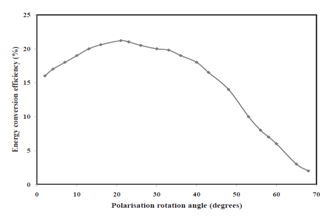 | Figure 8. Conversion efficiency with the variation of angle of crystal |
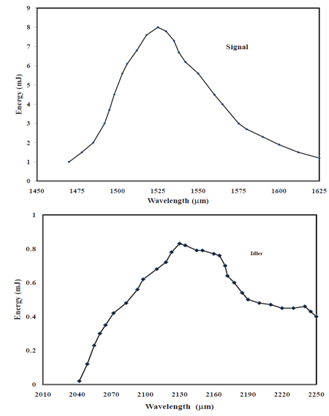 | Figure 9. Variation of signal & idler energy with wavelengths |
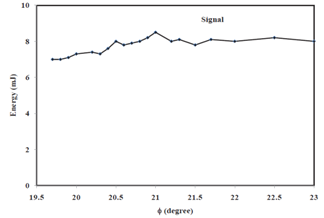 | Figure 10. Signal energy at a polarization angle |
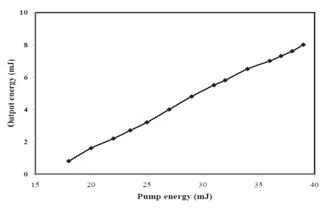 | Figure 11. OPO energy as a function of pump energy |
4. Conclusions
- Thus Optical parametric devices generate broadly tunable coherent optical radiation by the phase-matched nonlinear interaction of an intense laser beam in a suitable nonlinear crystals such as KTP etc. In this process the high energy pump photon is converted into a pair of lower frequency signal and idler photons while conserving the total energy and momentum. Tunability of the signal-idler pair is usually achieved either by changing the crystal birefringence through its temperature dependence or by the angular dependence of the extraordinary index of the crystal. In summary, we have demonstrated the operation of Nd:YAG eye-safe laser, pumped with two-dimensional side pumping diode-laser array. The wavelength from the Nd:YAG is 1.064 μm, which is not safe for the eye. The diode array is pulsed at 50 Hz, at power of 12 W, and energy of 120 mJ, pumpes the Nd:YAG laser operating at 1064 nm, and generates a 40 mJ pulse. A singly resonant extracavity KTP OPO pumped by this pulsed Nd:YAG laser. The output energy is an eye safe radiation at 1525 nm, with 8 mJ, corresponding to an energy conversion efficiency of 21 %, in a type-II, NCPM x-cut KTP crystal (15×10×10 mm) placed in a plane-parallel resonator. The measured OPO threshold pump intensity is in good agreement with the theoretically one. The KTP crystal is used so that when pumped at 1064 nm, it is simultaneously phase matched for optical parametric generation at the signal and idler wavelengths. The KTP crystal is cut along the θ= 900 =210 direction. The OPO output principally is a signal beam at 1525 nm, which beyond the ocular region, hence the output laser is safe for eye.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML