1. Introduction

With increasing demands in optical communication and sensing systems, optical ring resonators (ORR) with different structures[1-6], have been analyzed and proposed for several applications such as polarization sensing[7], biosensing[8], optical filters[9-14], optical fiber dispersion compensation devices[15,16], optical integration/ differentiation and optical triggering[2]. optical bistability[17,18], add/ drop multiplexer[19], optical switching[20-23], and various other applications[24-30]. In early work, steady state[2,31] and dynamic responses of ORR built on fiber were analyzed[32,33] for applications in polarization sensing[7], FM deviation measurement of a laser diode[33], optical triggering, optical integration/differentiation and fiber dispersion compensation[2], and rotation sensing[31]. Recently, dynamic resonance characteristic of fiber ring resonator has been analyzed for gyro system[34].

A basic structure of an ORR consists of a 2×2 directional coupler where one of the input port is connected to one of the output port, making a closed loop to configure a ring resonator. To operate an ORR at resonance, the loop length could be of the order of few micrometers[10] to tens of meters[32].

Recently, a full steady-state analysis of the ORR is reported where characteristic parameters such as coupling coefficient of the coupler and transmission parameters of the loop fiber affecting the response are investigated[35]. In another report, the dynamic behavior of the ORR, by considering the influences of light-source parameters on the response, is presented[36].

An ORR may be realized mainly by two types of configurations: Cross-coupled and direct-coupled. To the best of our knowledge, in the reported analyses of the ORR in the literatures, the importance and difference of these configurations have not been addressed with application point of views. With respect to the type of high power applications of ORR, variety of configuration may play an important role[37-39].

In this paper, we analyze the two ORR configurations and compare their characteristic intensities at the output and in the resonance loop[35]. It is shown that in one configuration the, the resonance loop intensity is about twice the other one.

2. ORR Configurations and Response Formulation

2.1. Intensities of Output and Resonance Loop

The two ORR configurations, which are considered for analysis, are shown in Fig. Fig. 1(a), a previously reported configuration[35] is shown in which the resonance loop is made by connecting two cross-coupled ports (2) and (3), whereas the resonance loop of our suggested ORR configuration in Fig. 1(b) is made by connecting two direct-coupled ports (2) and (4).

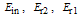For cross-coupled ORR (CCORR) in Fig. 1(a), let us assume that the loop and the coupler are ideal with no polarization coupling and the birefringence in the loop fiber is zero. In Fig. 1(a), if we denote and 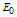the electric fields of light waves at ports (1), (2), (3), and (4), respectively, the complex field amplitudes at ports (3) and (4), under steady state operation, can be expressed as[1,35].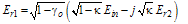

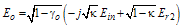
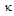(1)

(2)

Where is the power coupling coefficient of the coupler and 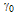is its fractional intensity loss.

For an ideal condition and based on conservation of energy[35,40], the electric fields 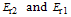are related by: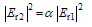

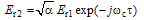
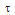(3)

(4)

where is the loop delay time, 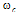is the optical angular frequency, and 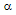is the power transmission coefficient of the loop fiber expressed as 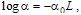, where 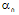is the attenuation coefficient (in dB/m) of the loop fiber, L is the length of the loop (in m).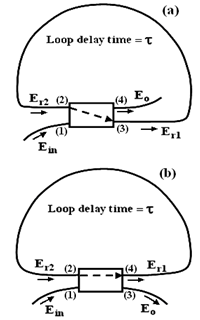

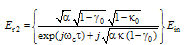
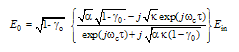
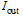Figure 1. Schematic diagrams of optical ring resonators (a) cross-coupled and (b) direct-coupled configurations

From Eqs. (1), (2), and (4) we can obtain the field at port 2[35]:

(5)

Substituting Eqs. (1), (4), and (5) in Eq. (2), E₀ results in:

(6)

2.2. Intensities of Output and Resonance Loop

By some algebraic manipulations of Eqs. (5) and (6), the output intensity at port (4) and the loop intensity 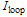at port (2) both normalized to input intensity can be shown, respectively, as: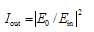

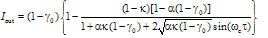
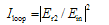
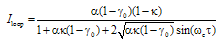
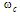(7)

(8)

(9)

(10)

2.3. Condition for Resonance

The condition for resonance in the ORR is obtained by finding the value of at which the loop intensity 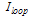builds up to a maximum value and the output intensity 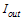reduces to a minimum value. By inspection of Eq. (8), the condition for resonance is found to be 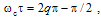, where q is an integer. Equation (8) shows that at resonance, the value of the output intensity 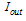becomes a minimum. The additional condition required to make 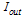to become zero at resonance can be shown as: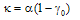

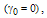(11)

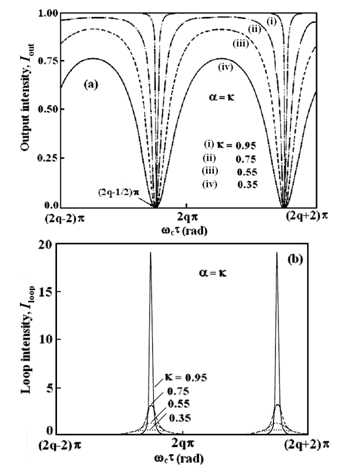
If the coupler is lossless we have 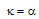. Figure 2 shows the theoretical output and loop intensities of the CCORR as a function of 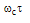for different values of .

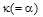We note that for all values of 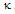, the output response dips to zero, and loop intensity peaks to a maximum value, indicating the resonance condition. As the value of 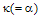decreases, the sharpness of the resonance response decreases as well.

When 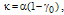, it can be shown that at resonance when 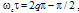, the maximum developed loop intensity 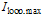is:

(12)

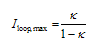
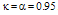The maximum value of the normalized loop intensity in this case is 19 for . A reduction of the value of 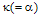from 0.95 to 0.75 causes the maximum loop intensity to decrease from 19 to 3. We note that in Fig. 2(b) the resonance response is not sharp when the value of 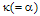is small.

2.4. Response of CCORR at Resonance

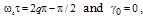From Eq. (8), at the normalized output intensity can be shown by: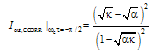

(13)

Figure 2. Normalized (a) output intensity and (b) loop intensity of CCORR with respect to and

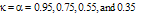
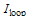From Eq. (10), can be derived as: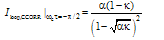

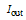(14)

Equation (13) gives the minimum value of at 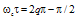as a function of 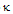and α. The normalized output intensity is equal to 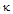for 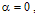, is zero when 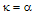, and is unity at 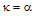. According to Eq. (14), under the resonance condition, if 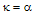, the theoretical value of tends to be large when κ tends to unity. But when 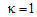, the power coupling in the coupler of the CCORR will be 100 percent, resulting in a zero loop intensity.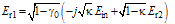

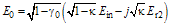
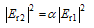
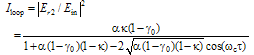
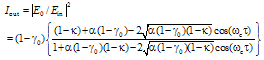
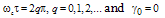3. Suggested Configuration of ORR

In this section, we analyze our suggested configuration of an ORR, as presented in Fig. 1(b), which is hereafter termed as DCORR. Principally, this configuration has a response similar to that of the CCORR discussed so far. The difference between the configurations of Fig. 1(b) and of Fig 1(a) is that in former port (4) is used for feedback loop instead of port (3) as in the latter case.

Under steady state operation, as in the previous section, the complex electric field at ports (3) and (4) of Fig. 1(b) can respectively be written as:

(15)

(16)

(17)

where all the parameters have their usual meaning. In a similar procedure, the normalized loop and output intensities can be shown as:

(18)

(19)

3.1. Response of DCORR at Resonance

The normalized loop intensity at resonance the condition from Eq. (18) can be shown as: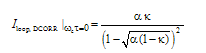

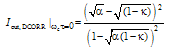
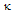(20)

(21)

In general, Eq. (21) gives the minimum value of the out put intensity as function of and 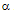. The additional condition for the output intensity 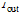to become zero at resonance is given by: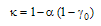

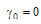(22)

For will be: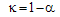

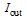(23)

Figure 3 shows the normalized output intensity of the DCORR as a function of 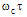and Fig. 4 illustrates the normalized loop intensity 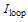, assuming 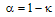and .

4. Comparison of CCORR and DCORR

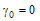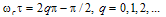If we compare Fig. 1 with Fig. 2, the responses of the CCORR and the DCORR indicate that the behavior is the same in both the cases except that the resonance in the former occurs at whereas in the latter it occurs at 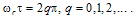. The major difference between two configurations lies in the value of 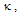, where in the DCORR, when value of 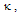is lower, the finesse of the resonator will be higher, while in case of the CCORR is reverse. Moreover, we note that at resonance conditions, at whatsoever value it maybe, the loop intensity in CCORR is nearly twice the value in the DCORR.

For practical reasons, the CCORR configuration in Fig. 1(a) is usually employed, since such a configuration can be fabricated by using a single length of an optical fiber without a need of any splice joint. To obtain high finesse or to make α as large as possible, it is desirable to avoid a splice joint in the loop fiber. To fabricate the configuration of DCORR in Fig. 1(b), two separate lengths of optical fibers would be needed to realize the coupler and a splice joint would be required to make the loop.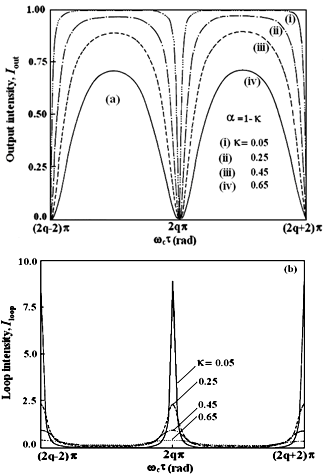

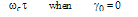Figure 3. Normalized (a) output intensity and (b) loop intensity of DCORR with respect to and

5. Conclusions

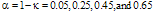
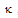This paper suggested a configuration for optical ring resonator having a resonance loop made of single-mode optical fiber. Under steady state condition, the responses of the proposed ORR are formulated by considering the output and loop intensities for various conditions of transmission coefficient α, power coupling coefficient , and compared the results with the previously reported ORR configuration.

The analyses have shown that the characteristic behaviors of both the configurations are the same. The main difference between two ORRs is due to the value of power coupling coefficient of the couplers used for their configurations. Another major point is that in CCORR configuration the loop power is nearly double of the value in the DCORR case.

The analytical results given in this article can be useful for selection of ORR configuration for particular applications, such as high power generation and investigation of nonlinear phenomena.