1. Introduction

As stated by Moore, the constituent’s quantities on a chip will twice every 18 months [1]. In recent times, existing metal oxide semiconductor (CMOS) archetype apprehends to its substantial confines and confronts certain defiant difficulties as challenges in the aspect size diminution and the extreme power utilization. Quantum-dot cellular automata are notable nanotechnology and one of the substitutes to switch the regular CMOS archetype with holding better density and swift switching momentum [2, 3]. QCA archetype is a united computation and conduction method to form logical circuits at nano-scale level and projected to perform with thicknesses of 10¹² devices/cm² in 100 GHz range [3-5]. These promote several researchers to perform novel circuits in QCA [6-18]. The layouts of Feynman gate have been explored in based on QCA [19-23]. Coplanar crossing based Toffoli gate has been introduced in [24]. A novel design of QCA based Toffoli gate has been presented in [25, 26]. This article represents the QCA outline of two imperative reversible gates such as Feynman and Toffoli gate. Besides, the energy depletion by the proposed designs is assessed that approves the outlook of QCA micro-device performing as are placement phase for the realization of reversible logic circuits. The firmness of the layouts beneath thermal randomness is assessed, presenting the effective proficiency of the proposed layouts.

This paper is organized as follows. In Section 2 the layout of the proposed Feynman and Toffoli gate is illustrated. The simulation and result comparison is presented in Section 3. Section 4 shows the energy utilization and consistency of the proposed layouts. Finally, the study is concluded in Section 5.

2. Proposed Reversible Gates

Reversible circuits have a wide range of application in low power logical circuit design [12, 18, 20, 22]. The total figure of outputs and inputs are identical in reversible gates. Whenever require to attain the number of outputs and inputs equal, an additional output or input can be adjoined. So, in a reversible logic circuit a one to one correlation between the outputs and inputs endures. Moreover, it should be designed with minimum amount of reversible gates, garbage outputs and quantum cost to have a better realization and least intricacy [15, 16].

2.1. Feynman Gate

Feynman is a 2x2 reversible gate containing a quantum cost equivalent to one. It is extensively utilized to present fan out in reversible circuits. The logical expression between the inputs (A, B) and outputs (P, Q) is presented by:

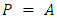(1)

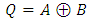(2)

The simulated circuit diagram of the proposed Feynman gate is given in Figure 1(a).

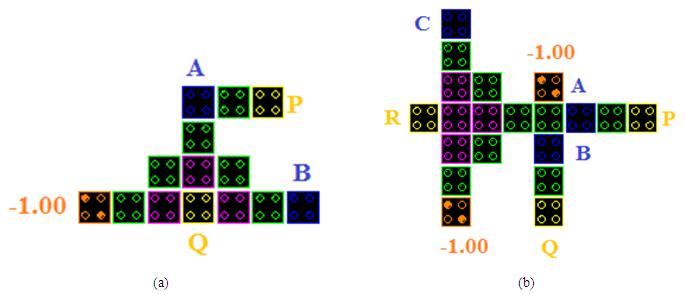Figure 1. Proposed QCA design of (a) Feynman gate, (b) Toffoli gate

2.2. Toffoli Gate

Toffoli is a 3x3 reversible gate having a quantum cost of five. In this reversible gate, the inputs (A, B, C) are associated to the outputs (P, Q, R) by:

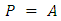(3)

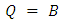(4)

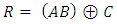(5)

In Figure 1, the QCA outlines of proposed Feynman and Toffoli gates are presented. These designs are realized using a novel 3-input XOR [27-29] gate and the gained the least number of QCA cells, covered space and without typical wire crossing. The proposed Feynman gate takes only 14 QCA cell with a region of 0.011μm² and with similar region Toffoli gate contains only 20 QCA cell. Regardless of allowing the substantially united QCA designs, not any of the wire crossing methods is operated to permeate the difficulties of wire crossing methods. Since in the multi-layer technique, double QCA wires within crossover permit through two distinct levels that absences a substantial realization as the assembling procedure would be complex because of its multi-layered type and assembling effort.

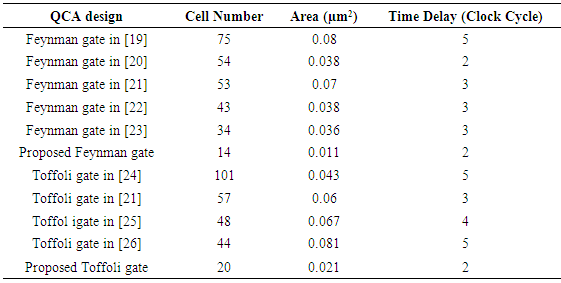
3. Simulation and Result Analysis

The simulations are attained by bistable simulation engine, QCADesigner [30]. The input-output waveform of the proposed Feynman and Toffoli gates is shown in Figure 2 (a) and (b) respectively. In Figure 2, the outcomes of bistable tool with the succeeding features are applied: relative permittivity 12.90, clock down 3.8×10⁻²³ J, clock up 9.8×10⁻²²J, amplitude factor of clock 2.00, and highest iterations per sample 100. It can be realized from Figure 2, the designs work acceptable and the outcomes of all proposed QCA circuits attain thorough extremely polarized signals that can present a top drivability for QCA circuits.

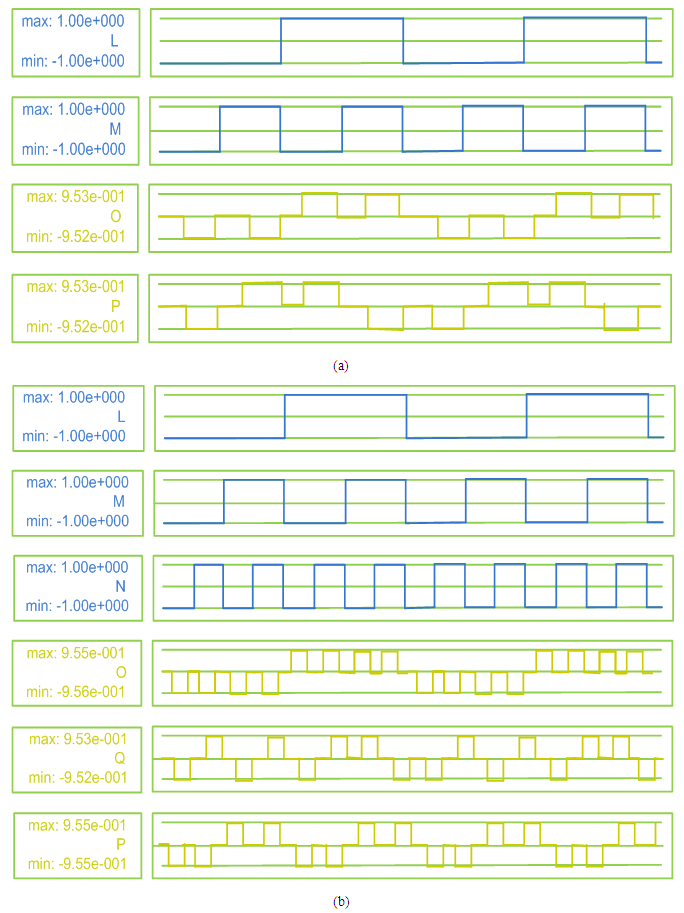Figure 2. Simulation outcome of the proposed QCA circuits (a) Feynman gate, (b) Toffoli gate

Table 1 presents comprehensive assessment among the proposed outlines and the earlier works. It is transparent that proposed designs are improved and optimized than all the former designs with a significant dominance. For instance, the proposed Feynman gate requires 81.33% less cells and occupies 86.25% less area compared to the design of [19]. In comparison with the earlier Toffoli gate [26], the imperative enhancements attained for the proposed Toffoli gate is 54.55% in the cells count, 74% in area. The overall enhancement is shown in Figure 3.

Table 1. Comparison of the proposed circuits with the earlier layouts

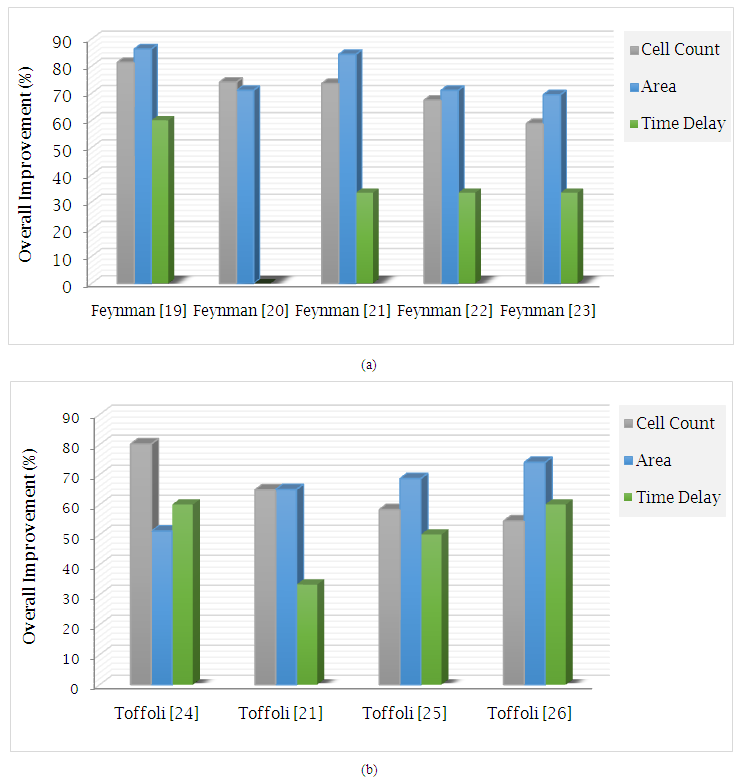Figure 3. Designing improvement achieved by the proposed (a) Feynman gate and (b) Toffoli gate over the previous design

4. Energy Depletion and Consistency Analysis

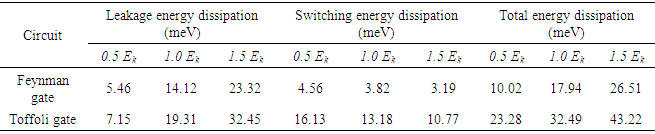
Every QCA cell shows equivalent energy depletion. Through procedure in single cycle, the depletion by the total circuit is projected by respecting the whole of energy depletion of all majority voters with inverters [31-33]. The QCAPro tools has been used to find the depletion of the proposed circuits at temperature T=2.0 K in separate channeling energy [34]. At 0.5 E_k tunneling energy level our proposed Feynman and Toffoli gate dissipate 10.02 meV e and 23.28 meV e respectively. The energy dissipation of proposed design at different tunneling energy level is given in Table 2 and the thermal map is shown in Figure 4.

The output polarization of any cell of the QCA layout is diminished by enhancing the temperature [16]. The process in [18] described the overall significance of output polarization. The temperature consequence on the output polarization of the proposed outlines is shown in Figure 5. From the figure, it is clear that both the design works proficiently between 1K to 10K. At the temperature 11K, the average output polarization drops dramatically and the design start malfunctioning.

Table 2. Energy dissipation of proposed design at different tunneling energy leve

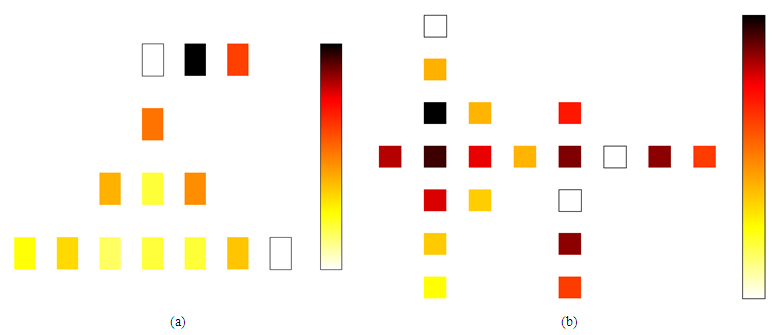Figure 4. Energy dissipation maps of (a) Feynman gate and (b) Toffoli gate at 2K temperature with 0.5 Ek tunneling energy level

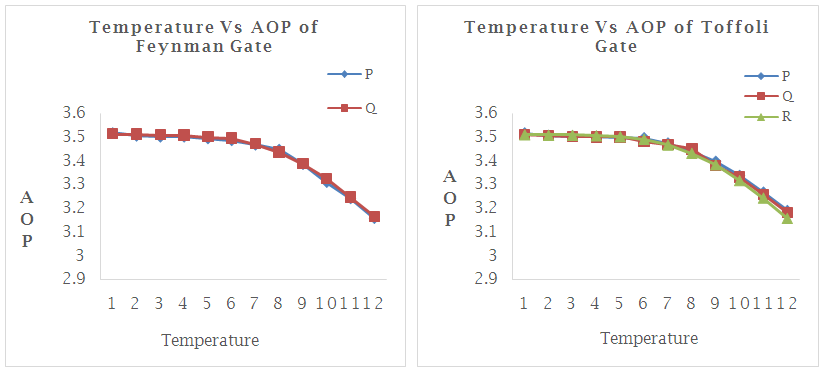Figure 5. Temperature consequence on output polarization of the proposed QCA layouts

5. Conclusions

In this paper, an efficient layout of Feynman and Toffoli gate has been presented in QCA technology. The proposed design is intense and has depleted latency than the existing design. Simulation outcome of the proposed circuit reveal the accuracy and efficacy. The proposed outlines are proficient to overcome the limitations of the earlier QCA design. These novel designs can be utilized as proper modules for fabricating of the low power consuming reversible nano communication device.