-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Nanoscience and Nanotechnology
p-ISSN: 2163-257X e-ISSN: 2163-2588
2016; 6(4): 62-67
doi:10.5923/j.nn.20160604.02

Simulation Investigations of Structural, Electronic, Optical and Elastic Properties of the CuxTi1-xO2
Yasaman Abed 1, Fatemeh Mostaghni 2
1Physic Department, Payam Noor University, Iran
2Chemistry Department, Payam Noor University, Iran
Correspondence to: Fatemeh Mostaghni , Chemistry Department, Payam Noor University, Iran.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

In this study, the electronic, optical and elastic properties of Cu-dopped TiO2 were theoretically investigated. The calculations have been performed using castep code in the framework of density functional theory with LDA and GGA approximations. Comparison between the experimental and the theoretical results indicates that the simulational method is able to provide satisfactory results for predicting the properties of the considered compounds. The best results were achieved by GGA+PBE approximation. It served as an additional proof of reliability of these theoretical findings and gave confidence in the results of the following calculations of the electronic, optical and elastic properties of Cu doped TiO2 semiconductor.
Keywords: Simulation, Electronic properties, Elastic constants, Semiconductor
Cite this paper: Yasaman Abed , Fatemeh Mostaghni , Simulation Investigations of Structural, Electronic, Optical and Elastic Properties of the CuxTi1-xO2, Nanoscience and Nanotechnology, Vol. 6 No. 4, 2016, pp. 62-67. doi: 10.5923/j.nn.20160604.02.
Article Outline
1. Introduction
- Among the inorganic oxide semiconductors, titanium dioxide is highly noteworthy due to its chemical stability, non-toxicity and low cost [1-5]. It is used in a wide range of fields, including pigments, solar energy transfer, photocatalyst and so on. Titanium dioxide exists in three crystalline phases includes rutile (cubic), anatase (tetragonal) and brookite (orthorhombic). Rutile, is the most stable phase of titanium dioxide in bulk and environmental conditions. It should be noted that the production of titanium dioxide, affects the final phase of production [6-10]. The mechanism of all its characteristics includes lighting the surface of titanium dioxide with energies greater than its band gap and exciting electrons from valance band to conducting band [11]. However, the use of titanium dioxide has been limited by two reasons [12]:1- The band gap of titanium dioxide is in the ultraviolet (UV), while less than 10% of sunlight is in the ultraviolet region of the spectrum.2- Rapid pairing of electron-hole which results in the loss of photo-catalytic activity.In recent years, the number of ways to modify titanium dioxide with metals and non-metals and sensitization of titanium dioxide have been used [13-15]. Different investigations show that doping of TiO2 by low amounts of metals and nonmetals elements, sometimes leads to enhanced photocatalytic activity and to an increase of visible light absorption [16, 17]. Producing solar cells based on titanium dioxide is the new generation of photo-volta cells that regarding its low cost have been proposed as an alternative to the solar cells [18]. In the area of solar energy, doping with Cu element significantly extends the light absorbtion of TiO2 into the visible region, which further enhance the photoelectro chemical properties of the TiO2 [19].The understanding of detailed electronic structure of semiconductors has been a challenging problem in electronics. Unfortunately, measurements of structure and electronic properties of crystals require a specified laboratory, as well as excellent quality materials, which is generally expensive. In contrast to experimental investigations, a theoretical analysis by computer simulations could overcome the effects of complex experimental factors and clarify the ion doping effects on crystal and electronic structure. Quantum chemistry calculations of modifying the band gap of TiO2 have been reported, including studies of transition metals co-doping of TiO2 photocatalysts [20-23]. Yalc et al. performed calculations based on density functional theory (DFT) to characterize the influence of Fe3+ doping on the electronic and structural properties of TiO2 [24]. Recently, first-principles calculations were conducted for Fe-doped TiO2 [25-28]. In our previous study we have performed a careful and systematic analysis of the cobalt impurity states in different concentrations as well as their influence on the TiO2 band structure and density of states [29].In this paper the electronic band structure, density of state, optical and elastic properties of Cupper doped TiO2 nanocomposite simulated using castep code. Castep employs the first-principles density functional theory that explore the properties of crystals and surfaces in materials, such as, semiconductors, ceramics, metals, minerals and zeolites.
2. Materials and Methods
- All presented calculations were performed using a first principle plane wave pseudo-potential technique based on density functional theory with CASTEP module [30] of Materials Studio. Calculations are performed with either generalized gradient (GGA) or the local density approximation (LDA) to treat the exchange–correlation effects. [31]. To obtain the desired accuracy, we selected 973 points in 6 × 6 × 7 K_point. Computations for TiO2 crystal are done in anatase phase (141/amd space group) with lattice constant a = b = 3.7834 and c = 9.4841. The structural data from ref. [32] were taken as an initial input for all calculations.
3. Results and Discussion
3.1. Electeronic Properties
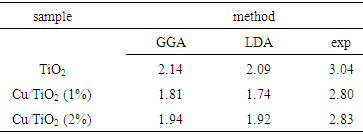
- In this study Cu dopant is substituted into anatase structure in Ti lattice site in various concentrations (0, 1 and 2%). Then the electronic structures and band parameters of three samples are obtained using either generalized gradient (GGA) or the local density approximation (LDA). From the above simulations, it is found that the band structure and density of states of three samples are nearly same from the LDA and GGA. The band gap values for all samples is determined from the band structures and density of state, by two methods. The results are summarized in table 1.
|
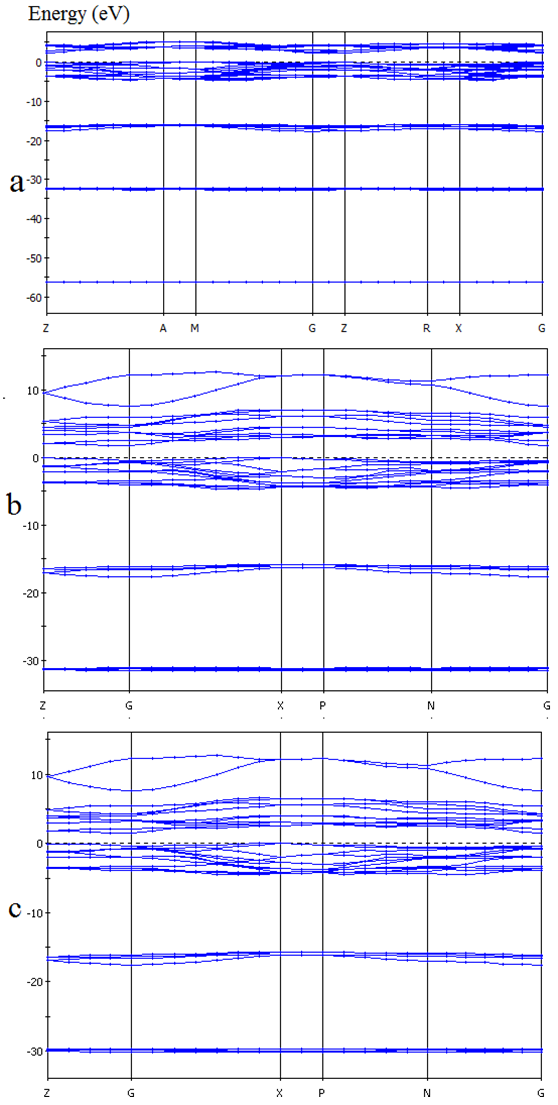 | Figure 1. Band structure and of CuxTi1-xO2 for (a) x= 0%, (b) 1% and (c) 2% in GGA method |
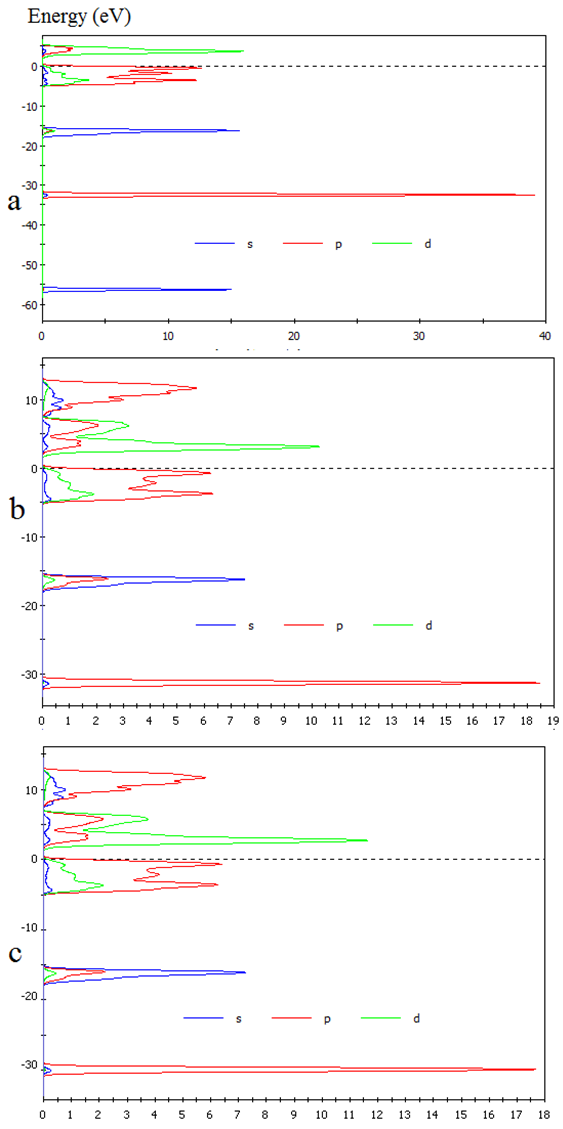 | Figure 2. Density of state of CuxTi1-xO2 for (a) x= 0%, (b) 1% and (c) 2% in GGA method |
3.2. Optical Properties
- The optical properties of matter can be described through the complex dielectric function ε(ω) as following [33]:ε(ω) = ε1(ω) + iε2(ω)The imaginary part of the dielectric function ε2(ω) is associated with the dissipation and as a consequence, it is responsible for the absorption. It is well known that the interaction of a photon with the electrons in the system can be defined in terms of time-dependent perturbations of the ground-state electronic states. If an incoming photon can couple a filled state to an empty state, there will be absorption. If there are a lot of photons which can couple these two states, there will be a big peak in the imaginary part of the dielectric function, because there will be more absorption.The ε2(ω) is obtained from the momentum matrix elements between the occupied and the unoccupied electronic states and calculated directly by [34]:
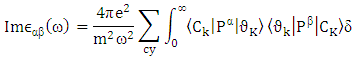
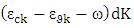 Where e is the electronic charge, Ck and υk are the conduction and valance band wave function at k respectively, and ω is the light frequency.The imaginary part calculations of the dielectric function for CuxTi1-xO2 for x = 0, 1 and 2% are shown in Figure 3.
Where e is the electronic charge, Ck and υk are the conduction and valance band wave function at k respectively, and ω is the light frequency.The imaginary part calculations of the dielectric function for CuxTi1-xO2 for x = 0, 1 and 2% are shown in Figure 3.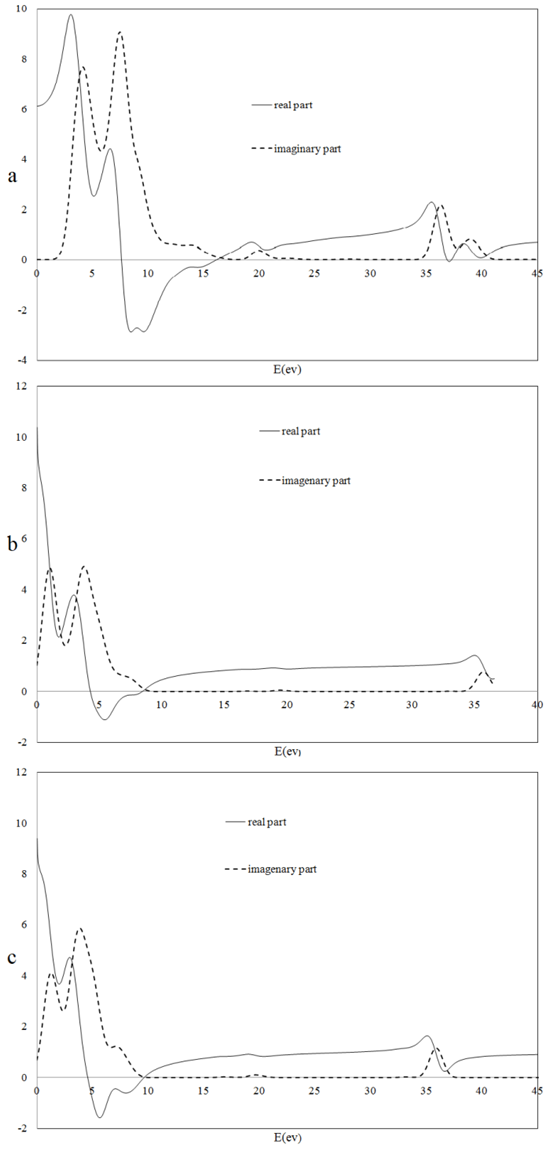 | Figure 3. The imaginary part of dielectric function for CuxTi1-xO2 for (a) x= 0% , (b) 1% and (c) 2% |
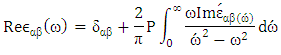 where P is the Kooshy integral section.The present results of calculated ε1(ω) are shown in Figure 3. An important quantity of ε1(ω) is the zero frequency limit ε1(0). It represents the dielectric response to the static electric field, which is the electronic part of the static dielectric constant and strongly depends on the band gap.In CuxTi1-xO2, value of ε1(0) increases from 6.14 to 10.37 and the direct band gap decreases With increasing the Cu concentration.
where P is the Kooshy integral section.The present results of calculated ε1(ω) are shown in Figure 3. An important quantity of ε1(ω) is the zero frequency limit ε1(0). It represents the dielectric response to the static electric field, which is the electronic part of the static dielectric constant and strongly depends on the band gap.In CuxTi1-xO2, value of ε1(0) increases from 6.14 to 10.37 and the direct band gap decreases With increasing the Cu concentration.3.3. Elastic Properties
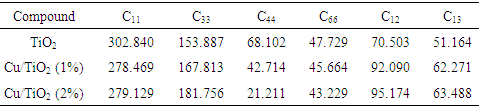
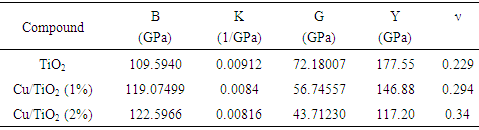
- The elastic constants of solids provide a link between the mechanical and dynamical behaviours of crystals. In the present work, we performed systematic first-principles calculations of the elastic constants Cij (Table 2), bulk moduli B, compressibility K, shear moduli G, Young’s moduli Y and the Poisson ratio v for CuxTi1-xO2 (Table 3).
|
|
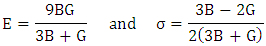 The calculated six independent elastic coefficients for each doping level were found to be positive and satisfy the known born criterion for a mechanically stable system: (C11+ C33- 2C13) > 0 C11> 0, C33> 0, C44> 0, C66 > 0, [2(C11+ C12) + C33+ 4C13] > 0 and (C11– C12) > 0). To define true polycrystalline constants, the values for their upper and lower limits were given by Hill. He showed polycrystalline moduli in terms of voigt and reuss approximation, and are given by [37].Hill’s shear modulus:
The calculated six independent elastic coefficients for each doping level were found to be positive and satisfy the known born criterion for a mechanically stable system: (C11+ C33- 2C13) > 0 C11> 0, C33> 0, C44> 0, C66 > 0, [2(C11+ C12) + C33+ 4C13] > 0 and (C11– C12) > 0). To define true polycrystalline constants, the values for their upper and lower limits were given by Hill. He showed polycrystalline moduli in terms of voigt and reuss approximation, and are given by [37].Hill’s shear modulus: 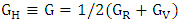 Hill’s bulk modulus:
Hill’s bulk modulus: 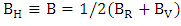 Where BR and Bv are the reuss’s and voigt’s bulk modulus and GR and Gv are the reuss’s and voigt’s shear modulus, respectively. From our calculations, it is found that the CuxTi1-xO2 is stiffer than the pure anatase TiO2, because the balk modul of Cu/TiO2 was bigger than pure TiO2. The Poisson's ratio (σ) takes the value: 0 < σ < ½. The lower limit and upper limit for central forces in solids are σ = 0.25 and σ = 0.5 respectively. The present calculated result showed that poisson's ratio (σ) of TiO2 and CuxTi1-xO2 was larger than the lower limit value (σ = 0.25), which indicates that the interatomic forces of CuxTi1-xO2 are central forces.
Where BR and Bv are the reuss’s and voigt’s bulk modulus and GR and Gv are the reuss’s and voigt’s shear modulus, respectively. From our calculations, it is found that the CuxTi1-xO2 is stiffer than the pure anatase TiO2, because the balk modul of Cu/TiO2 was bigger than pure TiO2. The Poisson's ratio (σ) takes the value: 0 < σ < ½. The lower limit and upper limit for central forces in solids are σ = 0.25 and σ = 0.5 respectively. The present calculated result showed that poisson's ratio (σ) of TiO2 and CuxTi1-xO2 was larger than the lower limit value (σ = 0.25), which indicates that the interatomic forces of CuxTi1-xO2 are central forces.4. Conclusions
- Calculations based on density functional theory have been carried out. The calculated values are in good agreement with experimental results and few conflicts are due to density function failure. The results show that by increasing Cu, the energy gap decreases and finally dielectric constant will increase which satisfy the corresponding experimental data result. The Cu introduced two lone pair states just above to the valence band maximum. Therefore charge transfer (CT) processes from the TiO2 valence band to Cu(II) and from Cu(II) to the conduction band Occur upon visible light. In other word Cu doping reduced the band gap of TiO2 with an optimal doping concentration of 1%. The best results were achieved by GGA+PBE approximation. In addition, it is found that the CuxTi1-xO2 is stiffer than the pure anatase TiO2, because the balk modul of Cu/TiO2 was bigger than pure TiO2. In the area of solar energy, doping with Cu element that significantly extends the light absorbtion of TiO2 into the visible region, further enhance the photoelectro chemical properties of the TiO2.
ACKNOWLEDGEMENTS
- We would like to thank Fars Payam Noor University for their support and encouragements.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML