-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Nanoscience and Nanotechnology
p-ISSN: 2163-257X e-ISSN: 2163-2588
2014; 4(2): 27-33
doi:10.5923/j.nn.20140402.02
Thermal Effect on Buckling of Multiwalled Carbon Nanotubes Using Different Gradient Elasticity Theories
Mokhtar Bouazza1, 2, Khaled Amara2, 3, Mohamed Zidour2, 4, Tounsi Abedlouahed2, Adda Bedia El Abbas2
1Department of Civil Engineering, University of Bechar, Bechar 08000, Algeria
2Laboratory of Materials and Hydrology (LMH), University of Sidi Bel Abbes, Sidi Bel Abbes 2200, Algeria
3Department of Civil Engineering, University centre of Ain Temouchent, Ain Temouchent 4600, Algeria
4Department of Civil Engineering, University of Ibn Khaldoun, BP 78 Zaaroura, 14000 Tiaret, Algeria
Correspondence to: Mokhtar Bouazza, Department of Civil Engineering, University of Bechar, Bechar 08000, Algeria.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
The present paper examines the thermal effect on axially compressed buckling of a multiwalled carbon nanotube based on the gradient elasticity theories. The small-size effect, which plays an essential role in the buckling behavior with large aspect ratios under axial compression coupling with temperature change, is captured by applying different gradient elasticity theories including stress and strain. In this model, each of the nested concentric tubes is regarded as an individual column and the deflection of all the columns is coupled together through the van der Waals interactions between adjacent tubes.
Keywords: Effect of Temperature Change, Nonlocal Elasticity, Carbon Nanotubes, Buckling
Cite this paper: Mokhtar Bouazza, Khaled Amara, Mohamed Zidour, Tounsi Abedlouahed, Adda Bedia El Abbas, Thermal Effect on Buckling of Multiwalled Carbon Nanotubes Using Different Gradient Elasticity Theories, Nanoscience and Nanotechnology, Vol. 4 No. 2, 2014, pp. 27-33. doi: 10.5923/j.nn.20140402.02.
Article Outline
1. Introduction
- Carbon nanotubes (CNTs) possess many unique electrical, optical, thermal, and mechanical properties (see Dresselhaus et al [1] and references therein). They have low weight, high aspect ratio, extremely high stiffness, and sustain large elastic strain and failure strain. Such special features of CNTs make them promising candidates with excellent structural performance as novel nanometer scale electronic and mechanical devices. In particular, experimental evidence and theoretical results (Ajayan et al [2]; Chopra et al [3]; Iijima [4]; Iijima et al. [5]; Molina et al [6]; Treacy et al [7]; Yakobson et al [8]) show that carbon nanotubes hold great promise as a possible reinforcing phase in polymer composite materials. Such composite materials, reinforced with strong, high Young’s modulus CNTs (fibres), are very useful due to their excellent specific mechanical properties. High aspect ratio fibres added to a polymer matrix increase Young’s modulus and the strength of the composite. However, long CNTs (fibres) often easily buckle and collapse during composite manufacturing (Lourie et al [9]; Wang et al [10]). It is not possible to directly measure the mechanical properties of single nanotubes (Barber et al [11]; Yu et al [12]). Therefore, by studying the deformation and buckling modes resulting from the embedding of CNTs (fibres) in a polymer matrix, it is possible to estimate the strength of carbon nanotubes under compressive stresses.Multi-walled carbon nanotubes are composed of concentric layers of single-walled carbon nanotubes. When subjected to a compressive force, multi-walled carbon nanotubes bend at large angles and may start to elastically ripple, buckle, and form kinks. Recently, large strain deformation of single- or multi-walled carbon nanotubes involving compression, bending or/and torsion has been the subject of numerous experiments and molecular dynamic simulations [13–17]. Basically, there were two theoretical approaches to understanding the behavior of carbon nanobutes: atomistic molecular-dynamics simulations and continuum mechanics. Molecular-dynamics simulations have provided abundant results for the understanding of buckling behaviors of carbon nanotubes. However, moleculardynamics simulations are currently limited to very small length and time scales and cannot deal with the large-sized atomic system, due to the limitations of current computing power. Moreover, at the nanoscale, experiments are extremely difficult and expensive to conduct. As a result, the continuum mechanics models are expected for the theoretical analysis of buckling behavior of carbon nanotubes. Yakobson et al. [13] introduced an atomistic model for axially compressed buckling of single-walled nanotubes and also compared it with a simple continuum shell model. They found that the continuum shell model could predict all changes of buckling patterns in the atomistic molecular-dynamics simulations. However, the existing continuum shell model cannot directly be applied to investigate mechanical behavior of multi-walled nanotubes due to the presence of the van der Waals forces in multi-walled nanotubes [18–21].The present paper examines the thermal effect on axially compressed buckling of a multi-walled carbon nanotube. The effects of temperature, surrounding van der Waals forces between the inner and outer nanotubes are taken into account. Using different gradient elasticity theories, the effect of temperature change on the properties of axially column buckling is examined.
2. Nonlocal Constitutive Equations
- According to Hooke’s law within continuum elasticity theory, the stress components at any point in an elastic medium depend only on the strain components at the same position. Instead, for the nonlocal theory of elasticity, the stress components at a reference point x depend not only on the strain components at the same position but also on all other points of the body [22, 23]. This theory can satisfactorily explain some phenomena related to atomic and molecular scale such as high frequency vibrations and wave dispersion [24, 25]. Mathematically, the basic constitutive equations for anisotropic, homogeneous, nonlocal elastic body can be written as:
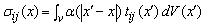 | (1) |
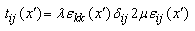 | (2) |
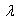 and
and 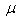 are Lame’s constants,
are Lame’s constants, 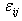 strain components, and
strain components, and 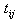 and
and 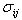 classical and nonlocal stress components, respectively. V is the volume occupied by the elastic body.Here α(x) is defined as the attenuation modulus of dimension length-3 and depends on the characteristic length ratio a/l, where a an is internal characteristic length (e.g. lattice parameter, granular distance of C–C bond length in carbon nanotubes) and l is an external characteristic length (e.g. crack length and wavelength). Alternatively, taking into account a typical characteristic of
classical and nonlocal stress components, respectively. V is the volume occupied by the elastic body.Here α(x) is defined as the attenuation modulus of dimension length-3 and depends on the characteristic length ratio a/l, where a an is internal characteristic length (e.g. lattice parameter, granular distance of C–C bond length in carbon nanotubes) and l is an external characteristic length (e.g. crack length and wavelength). Alternatively, taking into account a typical characteristic of 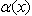 , the constitutive equations can be written in stress gradient form [22, 23], namely,
, the constitutive equations can be written in stress gradient form [22, 23], namely,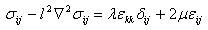 | (3) |
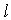 is a small scale parameter with length units describing the effects of the micro- and nano-scale on elastic behavior, and
is a small scale parameter with length units describing the effects of the micro- and nano-scale on elastic behavior, and 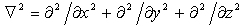 is the Laplacian operator. Here
is the Laplacian operator. Here 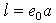 in which
in which 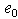 is a nondimensional material constant that can be determined by experiments or numerical simulations from lattice dynamics.In the case of stress gradient (nonlocal) theory the axial equivalent of Eq. (3) is expressed as
is a nondimensional material constant that can be determined by experiments or numerical simulations from lattice dynamics.In the case of stress gradient (nonlocal) theory the axial equivalent of Eq. (3) is expressed as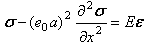 | (4) |
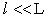 , higher powers of
, higher powers of  can be neglected and the solutions can be simplified to, giving [26]
can be neglected and the solutions can be simplified to, giving [26]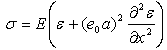 | (5) |
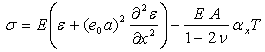 | (6) |
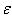 is the axial strain,
is the axial strain, 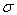 is the axial stress, a is the coefficient of thermal expansion in the x direction, E is Young’s modulus, and u is the Poisson’s ratio. For the axial force we have
is the axial stress, a is the coefficient of thermal expansion in the x direction, E is Young’s modulus, and u is the Poisson’s ratio. For the axial force we have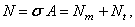 | (7) |
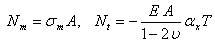 | (8) |
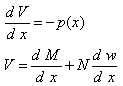 | (9) |
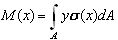 and noting that the relationship between strain and curvature for small deflections is
and noting that the relationship between strain and curvature for small deflections is 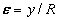 and that
and that 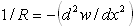 , where R is the radius of curvature and y is the coordinate measured positive in the direction of deflection [27], Eq. (6) can be rewritten as follows:
, where R is the radius of curvature and y is the coordinate measured positive in the direction of deflection [27], Eq. (6) can be rewritten as follows: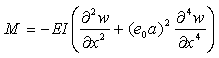 | (10) |
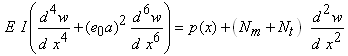 | (11) |
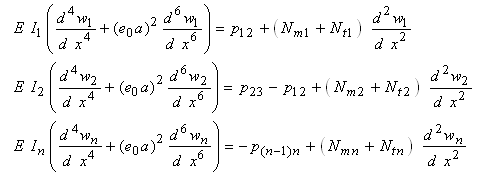 | (12) |
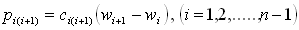 where ck(k+1) denotes the intertube interaction coefficient, which can be estimated by [33]where R (measured in cm) is the inner radius of each pair of nanotubes.Substitution of Eq. (11) into Eq. (10) gives
where ck(k+1) denotes the intertube interaction coefficient, which can be estimated by [33]where R (measured in cm) is the inner radius of each pair of nanotubes.Substitution of Eq. (11) into Eq. (10) gives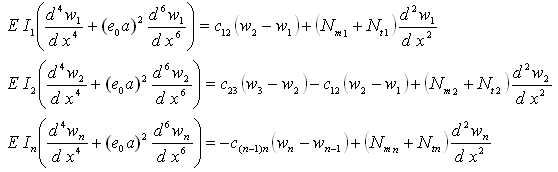 | (13) |
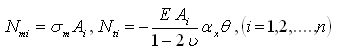 | (14) |
3. Analytical Solution for DWNT Using Stress Gradient Approach
- For simplification and without loss of generality, the nonlocal axial column buckling of a DWNT with a large aspect ratio is considered. In this case, Eqs. (13) become
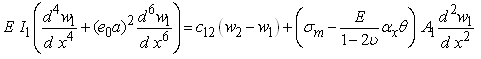 | (15a) |
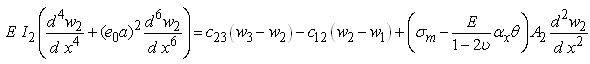 | (15b) |
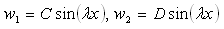 | (16) |
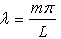 where C and D are real constants, and m is a positive integer which is related to buckling modes. Introduction of Eqs. (16) into Eqs. (15a) and (15b) yields
where C and D are real constants, and m is a positive integer which is related to buckling modes. Introduction of Eqs. (16) into Eqs. (15a) and (15b) yields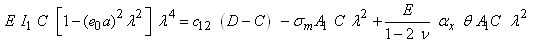 | (17a) |
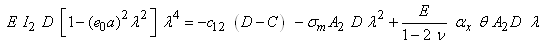 | (17b) |
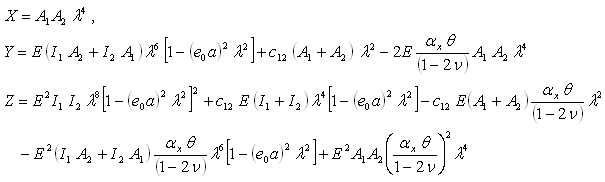 | (18) |
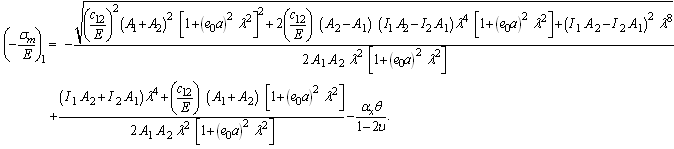 | (19a) |
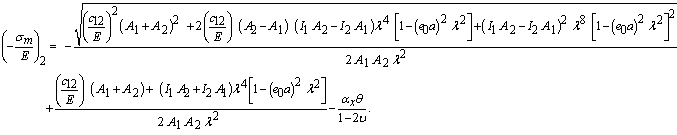 | (19b) |
4. Results and Discussion
- For the case of room or low temperature, we suppose α = -1.6x10-6 K-1 [35]. With the aspect ratio L/d1 = 60, the scale parameter e0a =0.5nm and the temperature change θ = 60 K, based on the relationship among the ratio stress/ classical and strain/ classical gradient elasticity theories, the m is indicated in Fig. 1. With m = 2 and θ = 60 K, the relationship among the ratio stress/ classical and strain/ classical gradient elasticity theories, the nonlocal parameter. With the e0a=1.5nm the aspect ratio L/d1 is shown in Fig. 2. It is clearly seen from Figs. 1 and 2 that the ratios stress/ classical and strain/ classical is less than unity. This means that the application of the local Euler–Bernoulli beam model for CNT analysis would lead to an overprediction of the critical axial buckling strain if the small length scale effect between the individual carbon atoms in CNTs is neglected. As the scale parameter m increases, the ratio strain / classical lower than value the ratio stress/ classical.For the case of high temperature, we suppose α = 1.1x 10-6 K-1 [35]. With the aspect ratio L/d1 = 60 and the temperature change θ = 60 K, the variation of the ratio stress/ classical and strain/ classical gradient elasticity theories, with the scale parameter e0a=0.5nm for various m is shown in Fig. 3. With m = 2 and θ = 60 K, the variation of the ratio stress/ classical and strain/ classical with the nonlocal parameter e0a=1.5nm for various aspect ratio L/d1 is shown in Fig. 3. It is seen from Figs. 3 and 4 that the column buckling strain for the DWNT is related to the nonlocal parameter e0a. It can be seen from Figs. 3 and 4 that the ratio stress/ classical and strain/ classical is less than unity, which is similar to the case of room or low temperature. Hence the critical axial buckling strain of the nanotubes based on the classical beam theory is over estimated aspect ratio L/d1 (length-to-diameter ratios) for m = 2 with different small scale parameter e0a. Therefore, it is clear that the small scale effect is significant for short CNTs. The comparison of small-scale effect in fig.2 and fig.4 are nearly identical.
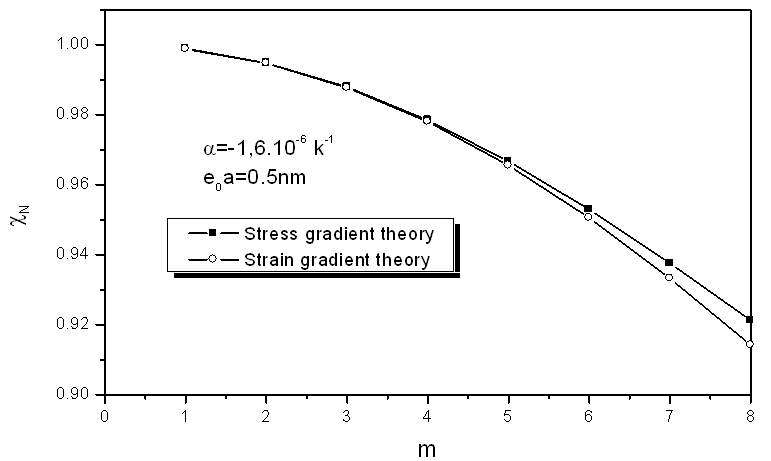 | Figure 1. Small scale effect on the critical axial buckling strain ratio of DWNT with the aspect ratio L/d1 = 60 in the case of low or room temperature (θ = 60 K) |
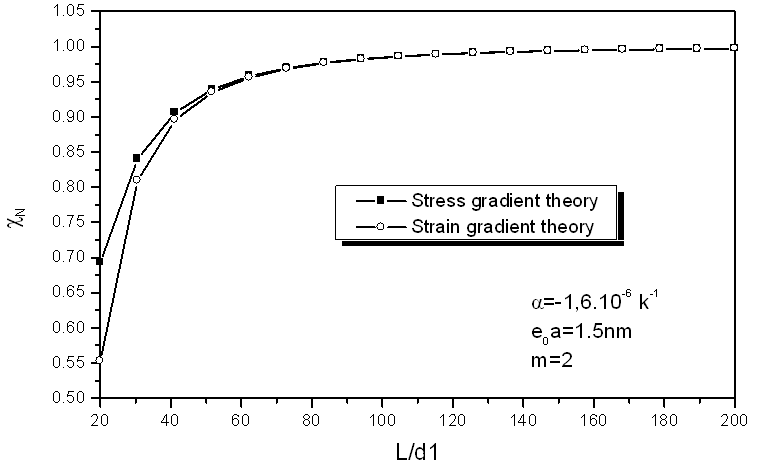 | Figure 2. Small scale effect on the critical axial buckling strain ratio of DWNT in the case of low or room temperature (θ = 60 K) |
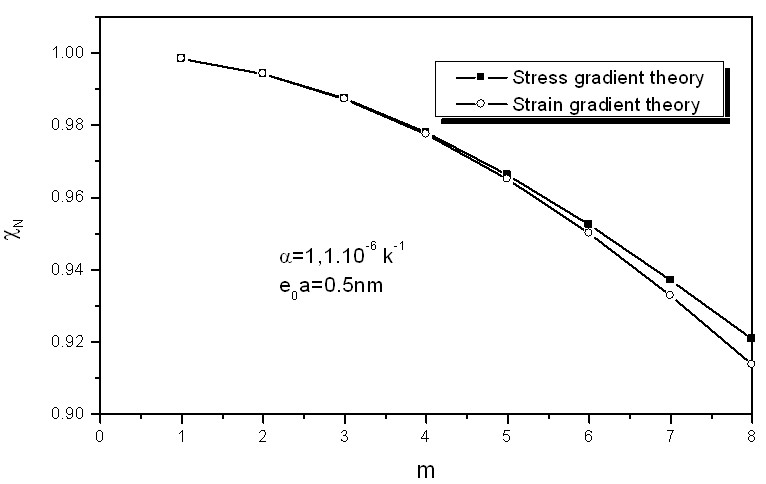 | Figure 3. Small scale effect on the critical axial buckling strain ratio of DWNT with the aspect ratio L/d1 = 60 in the case of high temperature (θ = 60 K) |
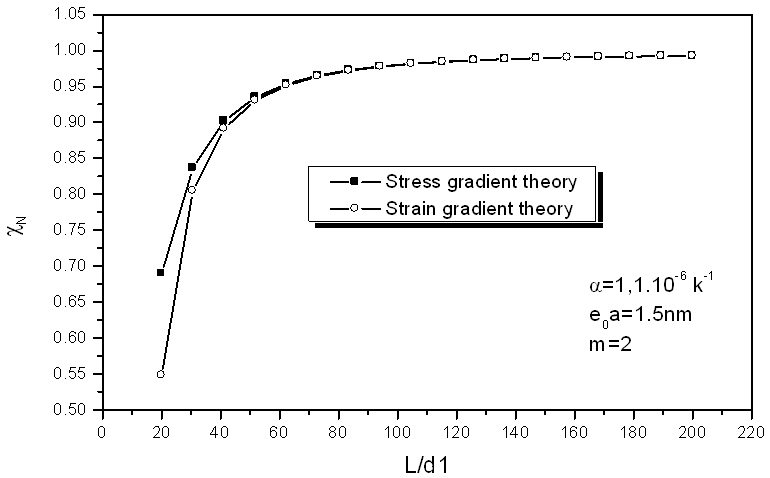 | Figure 4. Small scale effect on the critical axial buckling strain ratio of DWNT in the case of high temperature (θ = 60 K) |
5. Conclusions
- On the basis of theory of thermal different gradient elasticity theories including stress and strain, the theoretical formulations are established, based upon both the Euler–Bernoulli beam theory, is developed for column buckling of MWNTs with large aspect ratios under axial compression coupling with temperature change, which takes into account the effect of temperature change in the formulation incorporation of small length scale effects. In particular, an explicit expression is obtained for the critical buckling strain for a double-walled carbon nanotube. It is found that the thermal effect on the buckling strain is dependent on the temperature changes, the aspect ratios, and the buckling modes of carbon nanotubes. It is hoped that the analytical buckling solutions presented herein will be useful for research work on nanostructures.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML