1. Introduction

Semiconductor nanoparticles (NP), or quantum dots (QD) represent a unique class of semiconductor particles with sizes ranging between 2-10 nm in diameter. Within this size range, materials reveal unique optical and electronic properties resulting from quantum size effects. At present, greatest attention within semiconductor group А^IIB^VI [2; 3; 4] is paid to composite nanocrystals CdSe/ZnS of the core-shell type. Well-established and time-spaced synthesis phases [2] include nucleation and growth processes, and allow to obtain CdSe particles properly selected by size. Owing to their well-known advantages over organic fluorophores, CdSe / ZnS QDs are regarded as promising candidates to serve as a basis for development of new types of light-emitting devices [5; 6], biological object markers [7-10], and multi-colour laser devices [11].

The purpose of this study is theoretical and experimental analysis of quantum characteristics of fluorescent composite CdSe/ZnS NPs with cadmium selenide core and zinc sulphide shell, depending on CdSe core diameter. The notion of quantum characteristics implies a set of energy eigenvalues and a set of eigenfunctions of nonequilibrium charge carrier. The former of these sets is characterized by a well-known dependence on the nanoparticle sizes, which is interpreted within the so-called quantum size effect. It is natural to suppose that the latter, the set of eigenfunctions, should similarly be inherently dependent on nanoparticle sizes, if only because both sets are internally related and are different “sides” of the same solution. However, while dependence between the range of charge carriers’ eigenenergy values in nanoparticles and the nanoparticle sizes is widely used as a calibration curve in estimation of the said sizes, the dependence between the eigenfunctions range and nanoparticle sizes is still not even established with sufficient reliability. To establish this dependence based on calculations and measurements, as well as to apply the obtained dependence to solution of practical problems are the purposes of this study.

2. Calculations

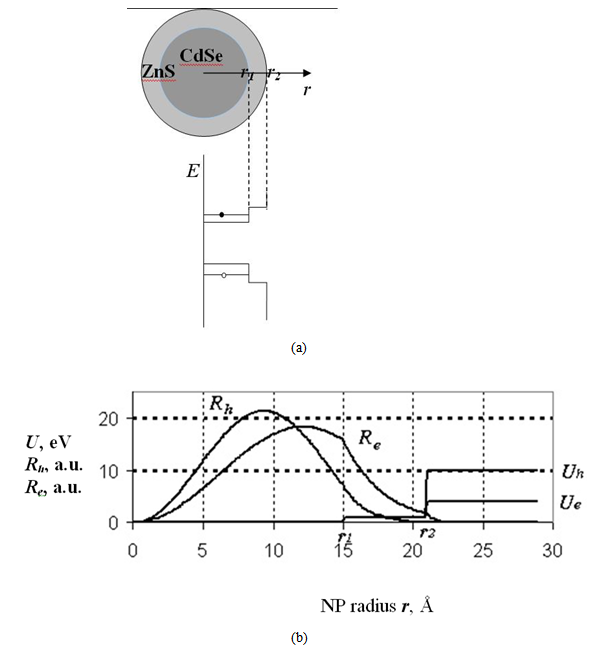
The quantum confinement effect of non-equilibrium charge carriers in nano-sized semiconductor particle causes changes in the whole range of its physical properties. This effect is sufficiently visible as nanostructure dimensions become smaller than or comparable to a certain parameter inherent to a given material, like, for example, Bohr exciton radius or electron wave length. There are also necessary conditions under which the probability of observing the quantum confinement effect increases as charge carrier scattering phenomenon appears. Such necessary conditions are the presence of a perfect crystalline structure, density and charge carriers’ free path length.

We have developed a computer program to realize a quantum “particle in the well” model [12] with step potential. A modified version of the program uses effective mass and barrier energy values of charge carriers in cadmium selenide and zinc sulphide. Dependences between major quantum characteristics of composite CdSe/ZnS nanoparticles and their sizes have been built for varying CdSe core diameter and ZnS shell thickness.

It should be noted that earlier the authors of this study [13] also used the simplest model of charge carrier localization in the potential well for interpretation of findings of nanoparticles’ physical and chemical property studies, including optical electron spectroscopy and X-ray photoelectron spectroscopy, X-ray structure studies within small and large angles of X-ray incidence and dispersion, transmission electron microscopy. This allowed us to explain why CdSe/ZnS nanoparticles have a higher quantum yield as compared to CdSe/CdS nanoparticles. Besides, we were able to demonstrate why ZnS shell is more advantageous than CdS shell. These facts are not trivial from the point of view of chemical stoichiometry and formation of dislocations at the core-shell border. However, zinc sulphide passivation provides a potential barrier increase for charge carriers at the border and facilitates an increased quantum yield of photoluminescence (PL) due to greater charge localization in the core. Besides, the choice of core thickness, optimal with regard to quantum-optical characteristics of nanoparticles, too, has been demonstrated by the authors of this study on the basis of a simple quantum-mechanical “particle in the well” model under the effective-mass approximation of non-interacting charge carriers.

Analysis of the charge carrier’s eigenfunctions is paid less attention to, though studies of size-dependence of spectral characteristics, such as transition oscillator strength and recombination probabilities of photo-excited charge carriers, require information on spatial overlap of the charge carriers’ eigenfunctions.

Let us consider the statement of the problem and the solutions obtained. The Schrodinger equation in the case of rectangular two-step potential well is presented as (Fig. 1):

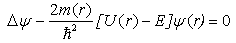(1)

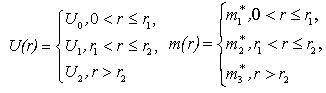(2)

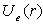and is solved for the electron (with potential ) and for the hole (with potential 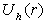) independently.

Figure 1. The model of spherically symmetric nanoparticle CdSe/ZnS: (a) r1 and r2.are the radii of CdSe core and ZnS shell; (б) dependence of step potential in CdSe/ZnS quantum well and radial probability densities Re and Rh for electron and hole on distance from NP centre r

Within the well, solutions are selected depending on parity of the state as:

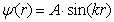or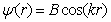

.

Outside the well, physically acceptable solutions have the form of:

,

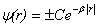where .

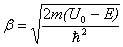The final solution with a view to the radial density of probability is presented as 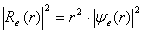for the electron and as 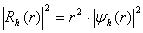for the hole. Proceeding from requirements of continuity and smoothness, matching should be provided at the potential borders, i.e., parameters should ensure that at the border area both the wave function and its derivative have the same values on both sides of the border. Since these conditions are only realized for certain 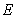values, a particle localized in a potential well has a discrete energy spectrum.

In our calculations, the Euler-Cromer method was supplemented with the requirement of constancy of probability current at the core-shell and shell-matrix borders.

The following parameters have been taken as initial for calculations were:

in CdSe core - 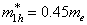, , 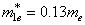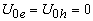eV;

at the core-shell border -

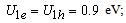in the organic matrix - , ;

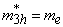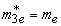at the shell-matrix border - ,

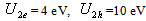where 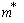is the effective mass, indices e and h indicate the parameter’s correspondence to the electron or the hole.

The shape of the well for the electron and the hole localized in a nanoparticle with CdSe core radius 15 Å and ZnS shell thickness 6 Å is given in Fig. 1. Fig. 1 also demonstrates radial probability densities Re and Rh for the electron and the hole. The hole, being a heavier particle, is seen to be localized closer to the core center. A kink is clearly visible on the electron’s radial probability density graph in the core-shell border area. It is less pronounced for the hole and results from an abrupt change of the charge carriers’ effective mass at this point.

Quantum confinement effects on the photoexcited charge carrier energy and electron transition oscillator strength have been studied theoretically by L.E. Bruce in [14]. Within very small crystallites (∼50 Å in diameter), a solution was obtained for Schrodinger equation with regard to Wannier excitons. In the process, kinetic energy operator was recorded using effective masses data for the electron and the hole, while potential energy operator was recorded using the expression provided by high-frequency dielectric electron solvation of atom cores. Oscillator strength of the electron transition assumes the following form:

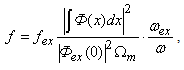(3)

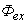where is the wave function 1s of the hydrogen atom state, 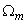is the volume of a single two-atom group CdS in crystallite, f_ex= 0.00256 is the oscillator strength value of bulk cadmium sulphide, and 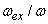is radiation frequencies ratio of bulk cadmium sulphide and small crystallite CdS. The obtained expression demonstrates that in small crystallites oscillator strength of electron transition only slightly depends on radiation frequency .

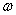Expression (3) for transition oscillator strength was presented by L.E. Brus for small CdS crystallytes. However, it is of a practically universal nature as it demonstrates the nature of dependence between the transition oscillator strength and the wave function overlap integral of photoexcited charge carriers, and thus contains information regarding the effects of quantum restraints on optical transition parameters. Oscillator strength is related to optical density, according to [15], as f = 4,32 10^-9 A, optical density A being expressed as molar extinction as per the well-known Bouguer-Lambert-Beer absorption law.

Figure 2 demonstrates dependencies between overlap integrals 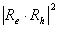and CdSe/ZnS nanoparticle diameters, calculated for the “particle in the well” model.

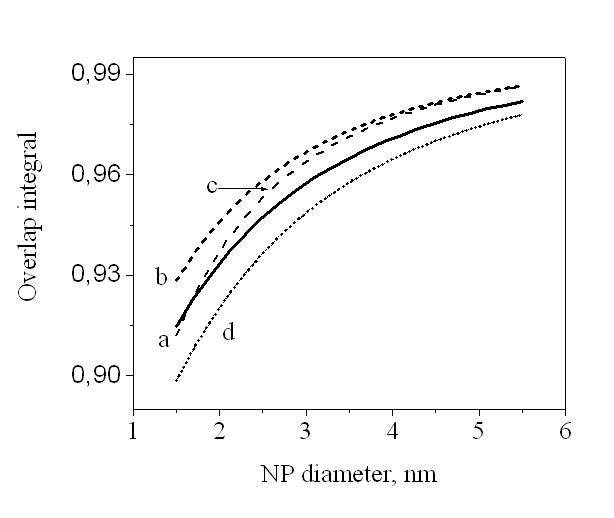Figure 2. Overlap integrals for eigenfunctioms of electron and hole in spherically symmetric nanoparticle CdSe/ZnS: (a) rectangular step potential; (b-d deformed on the shell surface

As may be seen from Fig. 2, within sizes smaller than Bohr exciton radius a_B (about 4.9 nm in the case of CdSe [1]), the electron and the hole wave function overlap integral increases monotonously as nanoparticle sizes increase. Transition oscillator force was further calculated according to formula (3).

3. Experimental Data

Let us now address experimental data. Fig. 3 demonstrates spectra of hydrophobic CdSe nanoparticles obtained from the manufacturing company Evidot as toluene dispersions, with CdSe core sizes ranging between 2.1 and 4.0 nm. The values of nanoparticle sizes were obtained from Evidot’s specification. Optical densities (Fig. 3, a) have the same values in all samples, with excitation wave length being 400 nm. PL spectra obtained under excitation at 400 nm are demonstrated in Fig. 3, b. The edge of the nanoparticle absorption band (Fig. 3, a) and the PL position band, depending on their sizes, tend to shift towards the shorter wavelength area as a manifestation of the quantum-size effect.

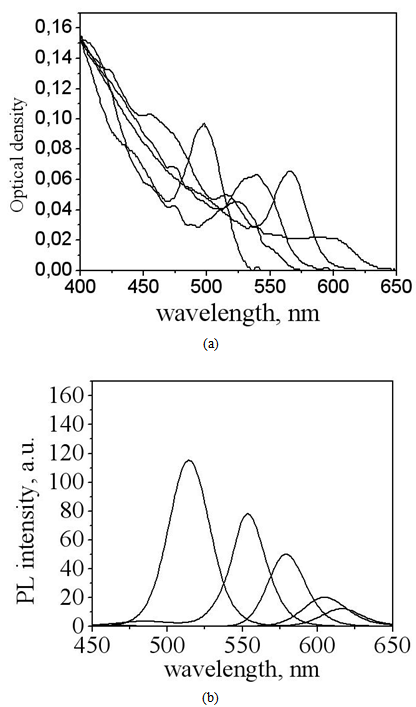Figure 3. Electronic spectra of CdSe/ZnS NP, dispersed in toluene: (a) optical density spectra; (b) PL spectra;

Figure 4 illustrates relationships between reverse values of transition oscillator strength (1/f) for the spherically symmetrical hole with rectangular graded potential (without border distortions) and mean PL decay time , on the one hand, and diameters d of toluene-dispersed CdSe/ZnS nanoparticles, on the other hand. PL mean decay time monotonously decreases as nanoparticle diameters d increase, similar to decrease in PL relative intensity (Fig. 3, b) as nanoparticle sizes increase.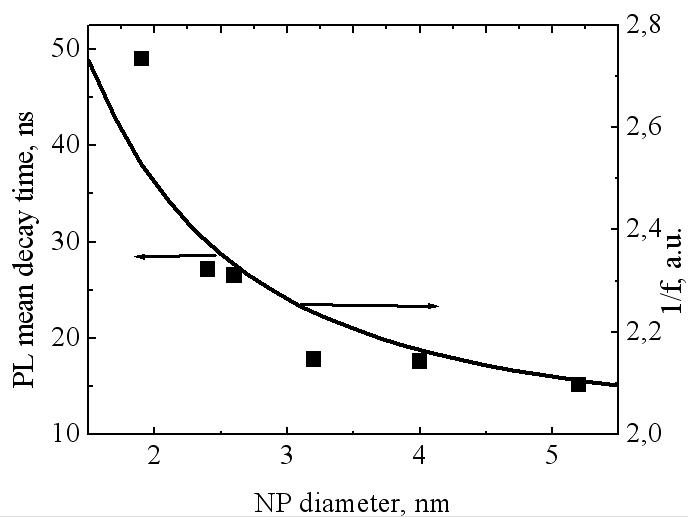

Figure 4. Dependence of quantum transition probabilities (1/f) and PL mean decay time 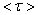(small squares) for CdSe/ZnS NP dispersed in toluene on there diameter d

4. Results and Discussion

Available published evidence on measurements of absorption cross-section, oscillator strength, and extinction coefficient with regard to nanoparticles is highly contradictory. Thus, for CdS nanoparticles, the authors of [16] presented dependence between the measured oscillator strength values of 1S_e − 1S_3/2h transition and radius r of nanoparticles within 5 to 1 nm range, including strong quantum confinement range.

It turned out that the sizes smaller than Bohr exciton radius a_B (about 2.7 nm in the case of CdS [1]) demonstrate an increase in transition oscillator strength as the radius decreases. Experimental data were well approximated by the function

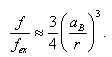(4)

It follows from approximation (4) that oscillator strength value accounting for one nanoparticle should not depend on its size. However, calculations performed by the authors of [17] demonstrated that absorption cross-section of CdSe nanocrystals, as estimated for a single volume and one nanoparticle, increases in line with nanoparticle radius increase. Summary spectral oscillator strength estimated for one nanoparticle increases too, following the linear law, as the radius increases.

A year later, the authors of [18] performed calculations of quantum characteristics of spheroid ZnS and CdSe nanoparticles with hexagonal crystal lattice (of wurtzite type). They used an empirical pseudopotential in the real base space. The electron transition parameters obtained in these calculations were compared to experimental data obtained by the same authors for ZnS and by the authors of [17] for CdSe. It turned out that in all three possible electric field polarization types, oscillator strength of 1S_e − 1S_3/2h transition should increase as ZnS nanocrystal radii increase from 5 to 15 Å. ZnS’s theoretical dependence obtained by the authors of this study correlates well with oscillator strength’s dependence on CdSe nanoparticle sizes measured by the authors of the previous study [31]. At the same time, in 2003, extinction coefficients were measured for CdTe, CdSe, CdS nanoparticles [19]. In particular, molar extinction coefficient in all three nanoparticle types demonstrated power-law increase as their radii increased. These experimental data are in obvious contradiction to other experimental data obtained a decade previously, in 1994, for CdS [16] and in 1993 for CdTe [20].

Thus, analysis of the published data demonstrates that, within the past two decades, the question whether electron transition probability in nanoparticles depends on their sizes was resolved in extremely contradictory ways. Transition oscillator strength either does not depend at all on particle sizes, or increases both with increase and decrease of particle sizes. Experimental findings obtained by different authors contradict each other, whereas theoretical prediction that oscillator strength should not depend on the particle size was made on the basis of a conclusion that the electron and the hole wave function overlap integrals increase as the particle sizes decrease in proportion to volume.

As is seen from Fig. 4, mean decay time also correlates with the calculated value obtained for estimation of nanoparticle radiative lifetime depending on their sizes. Thus, findings obtained from measurements of CdSe/ZnS nanoparticle decay kinetics demonstrate that oscillator strength in transition to the lowest 1S_e − S_h3/2 state depends on their sizes. This, most probably, is due to the well-developed synthesis procedure which provides sufficiently perfect crystal structure within a given sample batch. Under the conditions of a significant decrease in the number of defects, a band-to-band channel of charge carrier recombination may prevail in such samples. By band-to-band channel we mean 1S_e-1S_3/2h transition between the states which correspond to the lowest levels in the electron and the hole potential wells.

The presence of surface defects which potentially act as charge adhesion centers (traps) and open recombination channels through the levels of traps which lie in the forbidden zone (between HOMO and LUMO levels), most probably, affects nonradiative processes of excited state deactivation, the probability of radiative recombination through trap levels in the forbidden zone being negligible.

Indeed, as stated above, perfection of structure and absence of defects are the required conditions for size-dependent quantization effects in nanoparticles. The contradictions observed in literature for two decades are, evidently, due to the fact that those were the years of steady improvements in the synthesis of more and more perfect nanoparticles.

Nanosecond kinetics of charge carrier recombination (at room temperatures) in colloid CdSe nanoparticles of various sizes was studied by the authors of [21]. PL decay curves of colloid CdSe nanoparticles were demonstrated to be well approximated by the sum of two exponents. The authors link this fact to the two independent but spectrally overlapping processes. Firstly, it is recombinations of the so-called inner exciton with energy value very close to the width of the forbidden zone (E_g∼2 эВ) and lifespan about 20-30 ns, depending on the nanoparticle size (the slow component in the biexponential PL decay law). Secondly, it is recombinations of the so-called charged exciton generated in the charged nanoparticle while one of the photoexcited electrons is retained in the charge trap. This “charged” exciton generated in the conditions of self-induced Stark effect differs in energy from the “inner” exciton by the value ΔE of only about 20 meV, which ensures a good spectrum overlap of both recombination processes. However, mean lifespan of a “charged” exciton is about 1 to 3 ns (fast component in the measured PL decay kinetics). Interpretation of dependence between exciton decay time and nanoparticle size presented by the authors of [21] is, too, based on relationship between the forbidden zone width and exciton recombination probability.

Indeed, if the probability of the electron and the hole recombination through the levels located in the forbidden zone were great, the observed nanoparticle PL decay time should not depend on the band gap width and, consequently, on nanoparticle sizes. Numeric modeling performed by us was based on approximation of noninteracting electron and hole, whereas their recombination probability was estimated through probability of detection of both charge carriers in the vicinity of the same point in nanocrystal (wave function overlap integral). Coincidence of the nature of dependences in the charge carrier radiative recombination parameters in nanoparticles obtained in experimental way and within a primitive but quite fundamental “particle in the well” model may demonstrate that, for the given nanoparticle series, 1S_e − S_h3/2 band-to-band transitions may be a predominant recombination channel.

Another interesting finding obtained by us is the observed increase of PL quantum yield (Fig. 3, b) and increase of PL mean decay time (Fig. 4), as nanoparticle sizes decrease. These changes in both parameters, evidently, result from the same effect of quantum confinement increase as nanoparticle sizes decrease. These findings correlate well with dependence, observed by other authors, between PL quantum yield of CdSe/ZnS nanoparticles and their sizes [13].

Direct estimation of CdSe/ZnS nanoparticle PL quantum yield by measuring permanent emission spectra, using a standard reference solution, demonstrated the measurement findings to be dependent on free trioctylphosphine molecule content, as these molecules establish a certain dynamic sorption/desorption equilibrium on the nanoparticle surface. While real quantity of residual trioctylphosphine remains obscure, it becomes somewhat difficult to equalize optical densities of the nanoparticle and reference solutions. Within the scope of this study, a calibration curve of dependence between PL mean decay time and diameters of nanoparticles obtained directly after synthesis may be recommended for practical screening of nanoparticles with low PL quantum yield.

5. Conclusions

A correlation has been established for the first time between theoretical and experimental data regarding dependence between the electron transition oscillator strength and the relative PL quantum yield, on the one hand, and CdSe/ZnS nanoparticle sizes, on the other hand. The established quantum-size dependence of the electron transition oscillator strength may be interpreted as an indicator of the preferential radiative electron and hole recombination channel between the lowest 1S_e − 1S_3/2h levels in hydrophobic CdSe/ZnS nanoparticles. This, in its turn, may be characteristic for nanoparticles with a perfect crystal phase.

ACKNOWLEDGEMENTS

The study has been performed with financial support from Belarusian National Foundation for Fundamental Research (grants F05К-140, F07К-094, F10Р-232 и F11ОB-121).