Hussein H. Warid1, Abdul Kareem H. Dagher2
1Physics department, College of Sciences, Thi-Qar University, Nasiriyah, Thi-Qar, Iraq
2Physics Department, Education College, Al-Mustansiriyah University, Baghdad, Iraq
Correspondence to: Hussein H. Warid, Physics department, College of Sciences, Thi-Qar University, Nasiriyah, Thi-Qar, Iraq.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
In present work, we present simulation for the cross gain modulation (XGM) response of a quantum-dot laser (QD-LASER). an analytical model of XGM is derive by using four-level rate equation model (4LREM) under influence of external pumping in active region of (QD-LASER). In order to calculate the (XGM), (4LREM) modulated by add nonlinear self-gain saturation coefficient terms. Our date shows good agreement with other theoretical work.This serves to highlight how the modeling approach adopted can have a significant impact on the dynamic parameter values extracted from small signal measurements.
Keywords:
Quantum Dot Laser, Cross Gain Modulation, Rate Equation Model
Cite this paper: Hussein H. Warid, Abdul Kareem H. Dagher, Characteristics of High-peed Cross-Gain Modulation in Quantum Dot Lasers, Nanoscience and Nanotechnology, Vol. 4 No. 1, 2014, pp. 1-6. doi: 10.5923/j.nn.20140401.01.
1. Introduction
Wavelength converters are the key components in broadband networks. The next generation of high speed network and all it is functions need to transfer data by convert optical signals from one frequency to another to avoid wavelength-blocking and decrease the number of wavelength channels needed to operate a network.Wavelength conversion or frequency conversion mechanisms include cross-gain modulation (XGM), cross-phase modulation (XPM) and four-wave mixing (FWM) in semiconductor optical amplifiers (SOA). For high-speed uses, both XGM and XPM are limited by the carrier lifetime as they are dependent on interband carrier recombination and generation. According to our knowledge, there are several analytical models to calculate the XGM in semiconductor optical amplifier (SOA)[1]. In[2], by using two coupled rate equation model for carriers density and photon density an analytical model to calculate XGM response in semiconductor lasers is derive. The main goal of present work is investigation the modulation response in (QD-LASER). Due to gain saturation, high power signal at a is used to change the gain of a test laser by modulate the carrier density. The information transfer between pump wavelength and favorite test signal can be done by modulated favorite test signal in gain variation process. Coupled rate equations have been used widely to calculate the carrier dynamics and optical properties of QD-SOAs. Most published works that treat rate-equation models for these amplifiers consider only the electron dynamics. The hole dynamics is assumed to be so fast with respect to the electrons so that all the gain and spontaneous emission dynamical properties of the QDs are almost determined by the electron dynamics in conduction band. In the past, traditional modeling of bulk semiconductor lasers, involves describing the carrier (electron) and photon dynamics by a set of two coupled rate equations. Carriers are 3-D in nature and both equations are coupled through the processes of spontaneous and stimulated emission. Many of the features of all semiconductor lasers are well described by this approach, such as small signal response damping, turn on delay, relaxation oscillation under large signal modulation and pattern effects under high speed modulation. Based on rate equation model, there are several attempts to calculate the modulation response in semiconductor laser[3,4]. In[2], the last version for this subject is introduced. By using three-level rate equations model for (QW), an analytical model of the small-signal optical XGM theory is presented, take into account the escape/ relaxation lifetimes[5]. In present work, the modulation response of (QD-LASER), limited by the carrier lifetime as they are dependent on interband carrier recombination and generation in (QD-LASER). The paper is organized as follows. In Section II, we describe the four-level rate equations and an analytical model of the XGM in (QD-LASER). Results discussion in section III.
2. Four-Level Rate Equation Model and XGM Small-Signal Analysis
With neglected the barrier dynamics, 4lrem describe the carrier dynamics in four levels namely, ground state (GS), excited state, continuous state and wetting layer (WL). Different dots are interconnected through a two-dimensional wetting layer (WL). We can use rate equations model or master equation model to describe the electrons motion between wetting layer where the electrons are injected and the other states. in present model the continuous state and the excited state is the sources of electrons for (GS). the occupation probability of each state is dependent on the escape/relaxation lifetimes between this state and other states Some of these carriers recombine radioactively or/and nonradiatively in the WL and inside the QDs. The different processes (recombination, capture, escape, etc.) are illustrated in Fig. 1[1].The change in electrons density each state can be described as follows 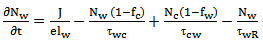 | (1) |
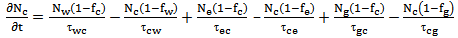 | (2) |
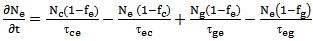 | (3) |
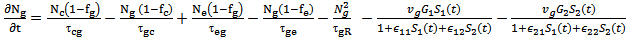 | (4) |
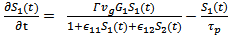 | (5) |
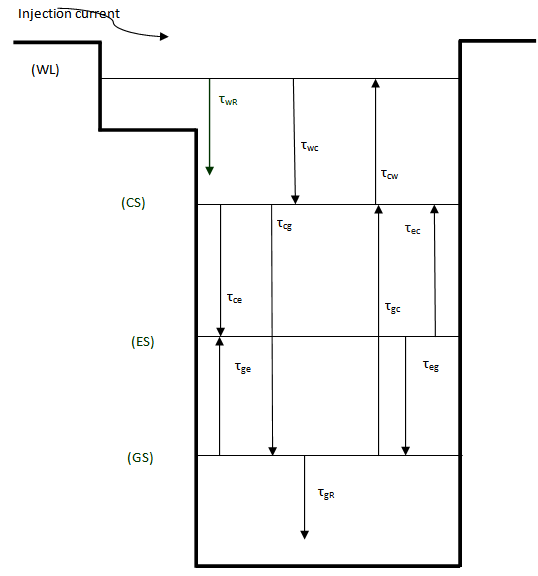 | Figure 1. Energy band diagram and the main processes[1] |
Where J is the injection current density, e is the electron charge,  is the thickness of the WL.
is the thickness of the WL.  and
and 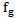 electron occupation probabilities corresponding respectively to WL, CS, ES, and GS respectively. The electron spontaneous recombination lifetimes in the WL and the GS are
electron occupation probabilities corresponding respectively to WL, CS, ES, and GS respectively. The electron spontaneous recombination lifetimes in the WL and the GS are 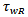 and
and 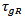 , respectively,
, respectively, 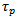 is the photon density,
is the photon density, 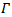 is optical confinement factor,
is optical confinement factor, 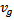 is the group velocity. Gain of test signal and pump signal is given by G1 and G2 respectively.
is the group velocity. Gain of test signal and pump signal is given by G1 and G2 respectively. 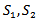 Are the photon density for the test laser and the pump laser respectively.
Are the photon density for the test laser and the pump laser respectively. 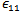 and
and 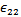 , which are the self-nonlinear gain saturation coefficients, and
, which are the self-nonlinear gain saturation coefficients, and 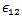 ,
, 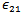 , which are the cross-nonlinear gain saturation coefficients.Under thermal equilibrium condition, the escape time and the relaxation time between any two states given by the following equation[1]:
, which are the cross-nonlinear gain saturation coefficients.Under thermal equilibrium condition, the escape time and the relaxation time between any two states given by the following equation[1]: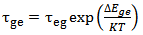 | (6) |
Where 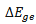 is the energy separation between the WL bandedge and the CS in the conduction band of QDs, K (Boltzmann's constant) =1.38×10-23J/K and T (room temperature) 300K. Figure 2, show the QD-laser structure in present work.In order to complete the small signal analysis, carrier density equation (N) and photon density equation (S) must be modulate to add the small signal terms for carrier density and photon densities. Thus, the expressions for carrier (electron) and photon densities are
is the energy separation between the WL bandedge and the CS in the conduction band of QDs, K (Boltzmann's constant) =1.38×10-23J/K and T (room temperature) 300K. Figure 2, show the QD-laser structure in present work.In order to complete the small signal analysis, carrier density equation (N) and photon density equation (S) must be modulate to add the small signal terms for carrier density and photon densities. Thus, the expressions for carrier (electron) and photon densities are 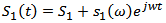 | (7a) |
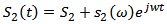 | (7b) |
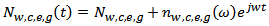 | (7c) |
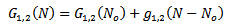 | (7d) |
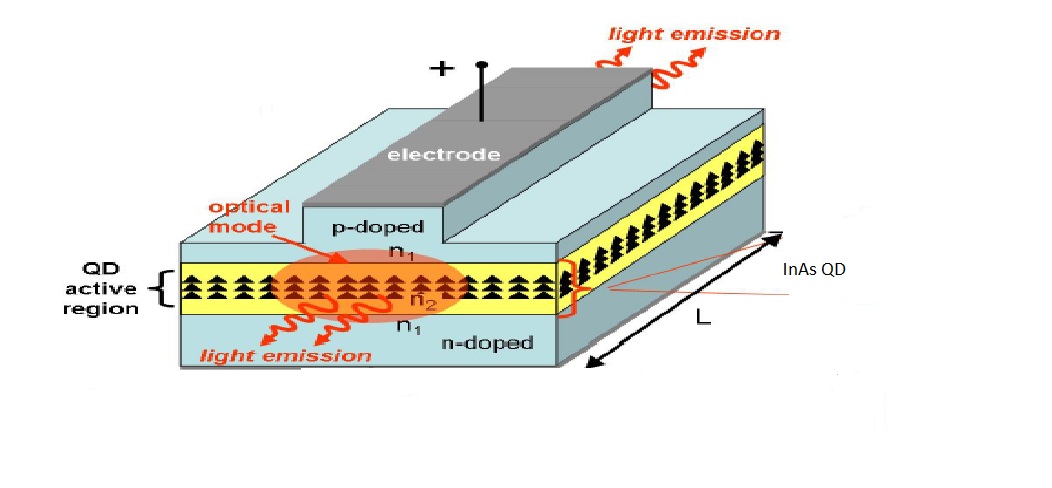 | Figure 2. 3-D Schematic of a QD p-i-n-doped semiconductor laser diode[6]. The z axis is the waveguide propagation axis, the yellow region is the active region, and is intrinsic (un-doped), and the black triangles represent the QDs |
By substitute Eq. (7a-d) in rate equation model Eqs. (1-5), we can write the small signal rate equation for the occupation probabilities and photon density as follows :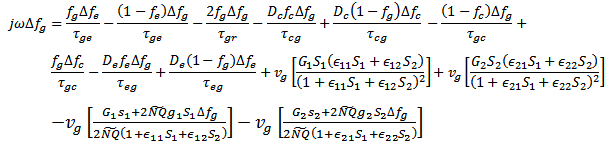 | (8) |
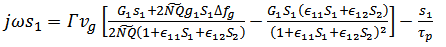 | (9) |
Where 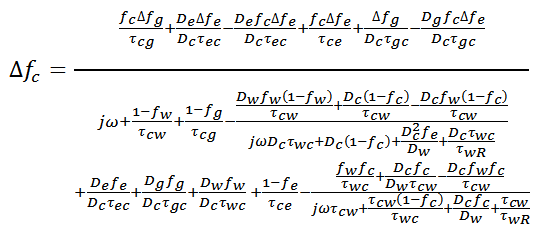 | (10) |
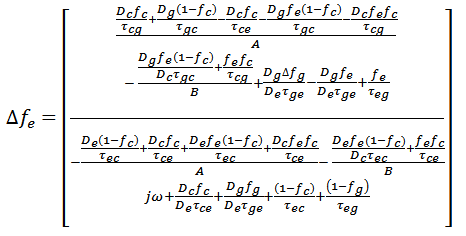 | (11) |
Where 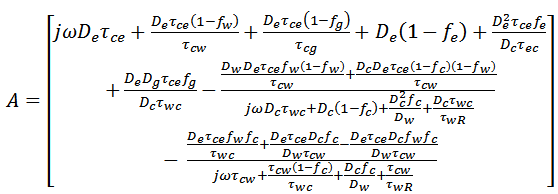 | (12) |
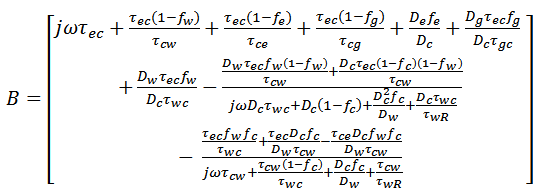 | (13) |
where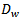 ,
,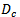 ,
, 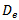 and
and 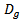 are the degeneracies of the corresponding electron states, the effective volume density of the QDs is
are the degeneracies of the corresponding electron states, the effective volume density of the QDs is 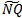 given by
given by 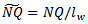 . After eliminating the (GS) occupation probability
. After eliminating the (GS) occupation probability 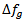 and solving for
and solving for 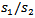 , the response is obtained
, the response is obtained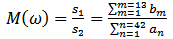 | (14) |
Denominator of Eq.14, includes an terms to the damping factor γ and the relaxation frequency 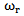 see appendix A. The terms
see appendix A. The terms 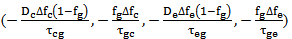 are neglected because it is not related to the values of
are neglected because it is not related to the values of 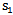 and
and 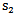 .
.
3. Results and Discussions
In present simulation, we have the following values[1,2], 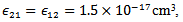 , nonlinear self-gain saturation coefficient
, nonlinear self-gain saturation coefficient 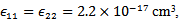 differential gain
differential gain 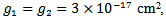 photon lifetime
photon lifetime 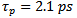 , group velocity
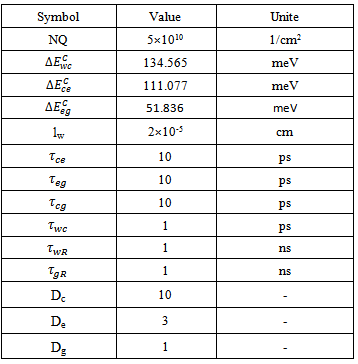
, group velocity 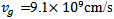 . The other values of the parameters used in QD-LASER modeling are listed in Table 1. The result for the XGM response at different values of pump power is displayed in Fig.3. The nonlinear property of material play major role in semiconductor devices. the propagation of strong pump signal in (QD-LASER) leads to cavity saturation i.e. we get gain saturation condition because the ultrafast carrier recombination (carriers depletion). This is leads to decreases in photon density of test signal and the peak of (XGM) responses. At high-pump level, the XGM response improves because the frequency terms in appendix A (damping terms ) has large values with pump power increasing i.e theses terms has small values at low-pump level. However, the most Important point in the current paper is to use the rate equations model with escape/relaxiation lifetimes can be increases the modulation bandwidth because it is present real describe to the carrier density in each levels in active region. in qd-laser simulation this necessary.
. The other values of the parameters used in QD-LASER modeling are listed in Table 1. The result for the XGM response at different values of pump power is displayed in Fig.3. The nonlinear property of material play major role in semiconductor devices. the propagation of strong pump signal in (QD-LASER) leads to cavity saturation i.e. we get gain saturation condition because the ultrafast carrier recombination (carriers depletion). This is leads to decreases in photon density of test signal and the peak of (XGM) responses. At high-pump level, the XGM response improves because the frequency terms in appendix A (damping terms ) has large values with pump power increasing i.e theses terms has small values at low-pump level. However, the most Important point in the current paper is to use the rate equations model with escape/relaxiation lifetimes can be increases the modulation bandwidth because it is present real describe to the carrier density in each levels in active region. in qd-laser simulation this necessary.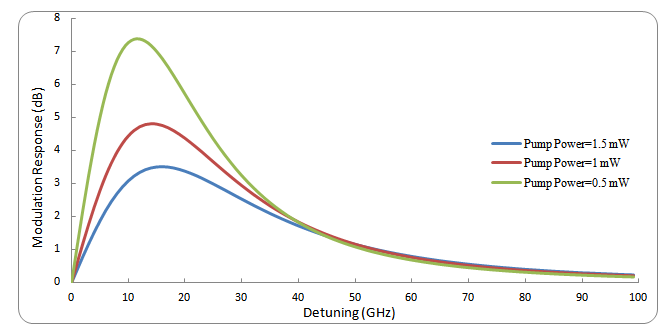 | Figure 3. The XGM response as a function of input pump power |
Table 1. Parameters Values at 1300 nm[1]
 |
| |
|
4. Conclusions
based on four-level rate equation model includes the nonlinear properties, we have introduced an analytical model to calculate the cross gain modulation response in quantum dot laser for the first time. As a result, the use of the four-level model described above potentially gives a more complete insight into the dynamics of (QD-LASER) and show major features in XGM response. This is comes from the effects of cross-gain-saturation when we are use two laser signal inside the quantum dot active region.
Appendix
The a’th and b’th in eq. 14 are given by 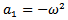 The damping factor terms are
The damping factor terms are 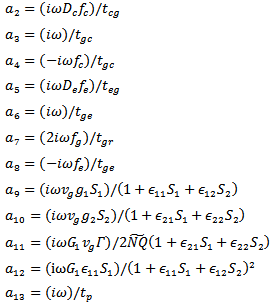 The relaxation frequency terms are
The relaxation frequency terms are 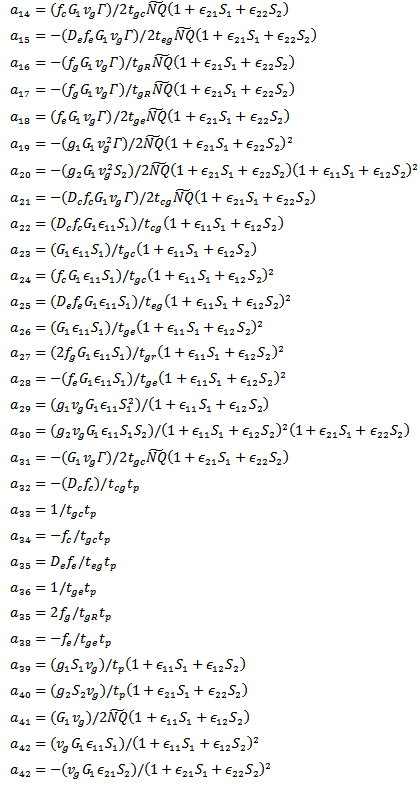 The Numerator terms are
The Numerator terms are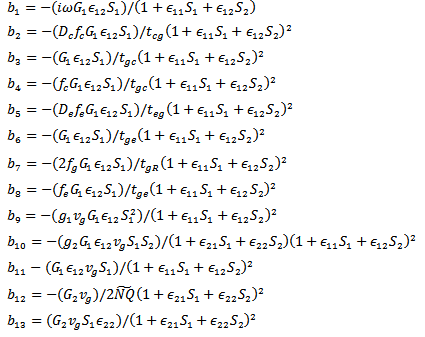
References
| [1] | R. S. Fyath, Abdul Kareem H. Dagher, and Hussein H. Warid, “Investigation of Cross Gain Modulation in Quantum-Dot Amplifier Using Four-Level Rate Equations Mode,” CIS J. vol. 3, no. 6, pp. 896-906, July 2012. |
| [2] | X. Jin, T. Keating, and S. L. Chuang, “Theory and Experiment of High-Speed Cross-Gain Modulation in Semiconductor Lasers,” IEEE J. Quantum Electron., vol. 36, no. 12 pp. 1485–1493, Dec. 2000. |
| [3] | L. Shao-Feng, I. Montrosset, M. Gioannini, S. Shu-Zhong, M. Jian-Wei, “Modeling and simulation of InAs/GaAs quantum dot lasers,” OPTOELECTRONICS LETTERS, vol. 7, n. 2, pp. 122–125, 2011. |
| [4] | L. V. Asryan, Y. Wu, and R. A. Suris, “Carrier capture delay and modulation bandwidth in an edge-emitting quantum dot laser,” Appl. Phys. Lett., vol. 98, no. 13, Art. no. 131108, Mar. 2011. |
| [5] | David McDonald, and Ronan F. O’Dowd, Comparison of Two- and Three-Level Rate Equations in the Modeling of Quantum-Well Lasers,” IEEE J. Quantum Electron., vol. 31,no. 11 pp. 1927-1934, Nov. 1995. |
| [6] | A. J. Zilkie, " High-Speed Properties of 1.55-µm-wavelength Quantum Dot Semiconductor Amplifiers and Comparison with Higher-Dimensional Structures," PH.D. Electrical and Computer Engineering. Thesis, University of Toronto, 2008. |

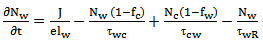
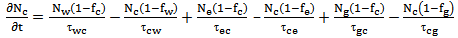
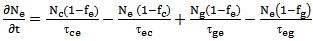
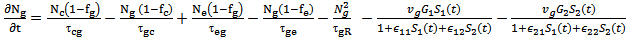
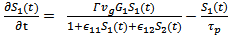

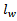 is the thickness of the WL.
is the thickness of the WL.  and
and  electron occupation probabilities corresponding respectively to WL, CS, ES, and GS respectively. The electron spontaneous recombination lifetimes in the WL and the GS are
electron occupation probabilities corresponding respectively to WL, CS, ES, and GS respectively. The electron spontaneous recombination lifetimes in the WL and the GS are 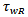 and
and 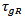 , respectively,
, respectively, 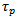 is the photon density,
is the photon density, 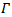 is optical confinement factor,
is optical confinement factor, 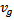 is the group velocity. Gain of test signal and pump signal is given by G1 and G2 respectively.
is the group velocity. Gain of test signal and pump signal is given by G1 and G2 respectively. 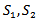 Are the photon density for the test laser and the pump laser respectively.
Are the photon density for the test laser and the pump laser respectively. 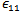 and
and 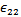 , which are the self-nonlinear gain saturation coefficients, and
, which are the self-nonlinear gain saturation coefficients, and 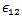 ,
, 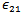 , which are the cross-nonlinear gain saturation coefficients.Under thermal equilibrium condition, the escape time and the relaxation time between any two states given by the following equation[1]:
, which are the cross-nonlinear gain saturation coefficients.Under thermal equilibrium condition, the escape time and the relaxation time between any two states given by the following equation[1]: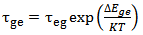
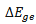 is the energy separation between the WL bandedge and the CS in the conduction band of QDs, K (Boltzmann's constant) =1.38×10-23J/K and T (room temperature) 300K. Figure 2, show the QD-laser structure in present work.In order to complete the small signal analysis, carrier density equation (N) and photon density equation (S) must be modulate to add the small signal terms for carrier density and photon densities. Thus, the expressions for carrier (electron) and photon densities are
is the energy separation between the WL bandedge and the CS in the conduction band of QDs, K (Boltzmann's constant) =1.38×10-23J/K and T (room temperature) 300K. Figure 2, show the QD-laser structure in present work.In order to complete the small signal analysis, carrier density equation (N) and photon density equation (S) must be modulate to add the small signal terms for carrier density and photon densities. Thus, the expressions for carrier (electron) and photon densities are 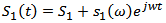
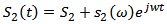
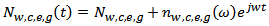
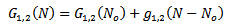
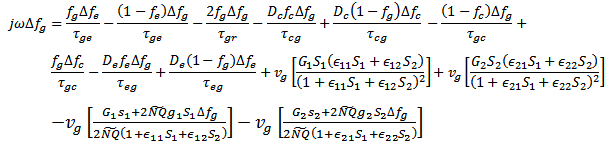
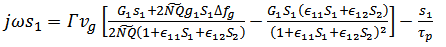
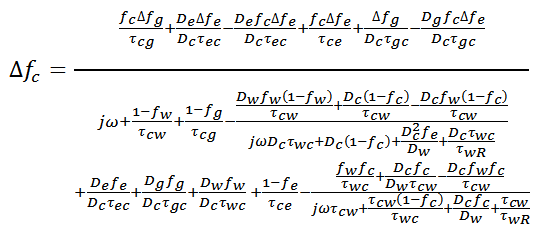
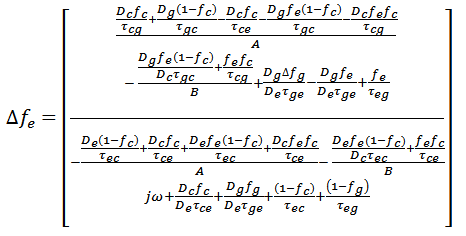
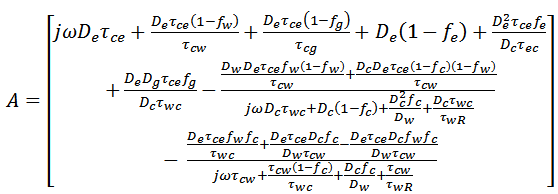
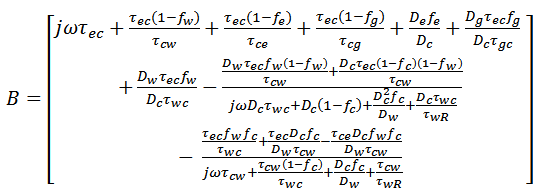
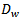 ,
,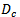 ,
, 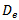 and
and 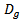 are the degeneracies of the corresponding electron states, the effective volume density of the QDs is
are the degeneracies of the corresponding electron states, the effective volume density of the QDs is 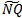 given by
given by 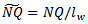 . After eliminating the (GS) occupation probability
. After eliminating the (GS) occupation probability 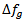 and solving for
and solving for 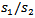 , the response is obtained
, the response is obtained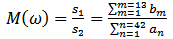
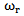 see appendix A. The terms
see appendix A. The terms 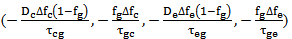 are neglected because it is not related to the values of
are neglected because it is not related to the values of 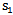 and
and 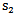 .
.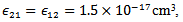 , nonlinear self-gain saturation coefficient
, nonlinear self-gain saturation coefficient 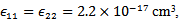 differential gain
differential gain 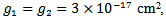 photon lifetime
photon lifetime 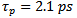 , group velocity
, group velocity 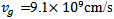 . The other values of the parameters used in QD-LASER modeling are listed in Table 1. The result for the XGM response at different values of pump power is displayed in Fig.3. The nonlinear property of material play major role in semiconductor devices. the propagation of strong pump signal in (QD-LASER) leads to cavity saturation i.e. we get gain saturation condition because the ultrafast carrier recombination (carriers depletion). This is leads to decreases in photon density of test signal and the peak of (XGM) responses. At high-pump level, the XGM response improves because the frequency terms in appendix A (damping terms ) has large values with pump power increasing i.e theses terms has small values at low-pump level. However, the most Important point in the current paper is to use the rate equations model with escape/relaxiation lifetimes can be increases the modulation bandwidth because it is present real describe to the carrier density in each levels in active region. in qd-laser simulation this necessary.
. The other values of the parameters used in QD-LASER modeling are listed in Table 1. The result for the XGM response at different values of pump power is displayed in Fig.3. The nonlinear property of material play major role in semiconductor devices. the propagation of strong pump signal in (QD-LASER) leads to cavity saturation i.e. we get gain saturation condition because the ultrafast carrier recombination (carriers depletion). This is leads to decreases in photon density of test signal and the peak of (XGM) responses. At high-pump level, the XGM response improves because the frequency terms in appendix A (damping terms ) has large values with pump power increasing i.e theses terms has small values at low-pump level. However, the most Important point in the current paper is to use the rate equations model with escape/relaxiation lifetimes can be increases the modulation bandwidth because it is present real describe to the carrier density in each levels in active region. in qd-laser simulation this necessary.
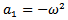 The damping factor terms are
The damping factor terms are 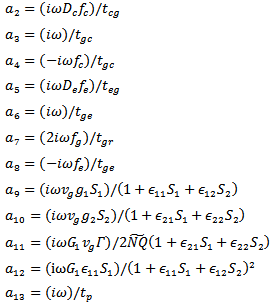 The relaxation frequency terms are
The relaxation frequency terms are 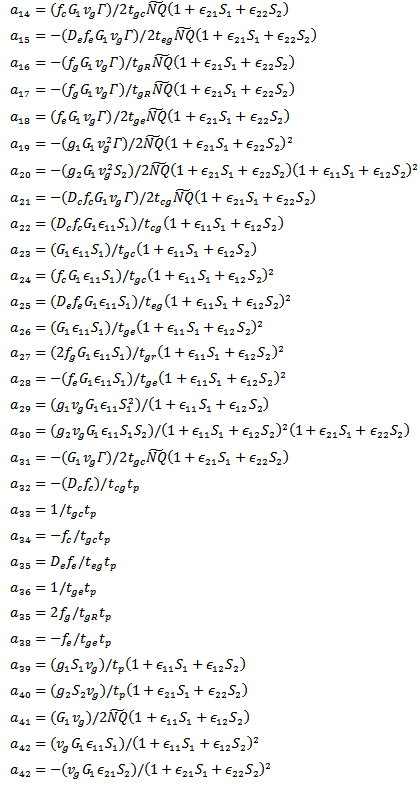 The Numerator terms are
The Numerator terms are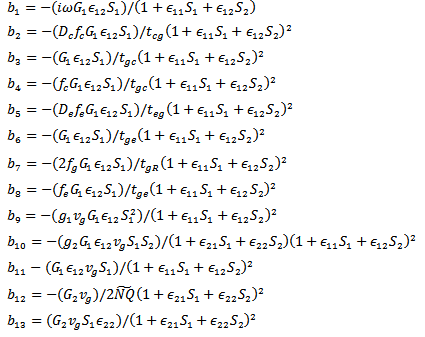
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
