M. H. Korayem , M. Geramizadeh
Robotic Research Laboratory, Center of Excellence in Experimental Solid Mechanics and Dynamics, School of Mechanical Engineering, Iran University of Science and Technology, Tehran, Iran
Correspondence to: M. Geramizadeh , Robotic Research Laboratory, Center of Excellence in Experimental Solid Mechanics and Dynamics, School of Mechanical Engineering, Iran University of Science and Technology, Tehran, Iran.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
During the recent years, one of the most important progresses in nano world was the development of methods for direct access to single molecules on the nanometer scale. The most significant ones have been the scanning probe microscopes such as the atomic force microscope (AFM). AFM is a versatile tool for imaging, force measurement and manipulation of different nanoparticles including proteins, DNA, and living cells. This work is focused on manipulation of biological cells specially DNA in biological liquid and is analyzed dynamics of the spherical nanoparticle manipulation based on Atomic Force Microscopy (AFM). In previous investigations, pushing of the gold nanoparticle using AFM was modeled in air and liquid and the dynamic behavior of tip and nanoparticle was investigated. The problem is simulated for DNA nanoparticle pushing on a silicon substrate in biological liquid using AFM. The biological liquid is ethanol in all the parts, but a comparison has been made between three liquids (ethanol, methanol and blood) in order to investigate the effect of environment on the results. The results show that, for DNA (as compared to gold), the required manipulation force and time for nanoparticle sliding and rolling increase by 17.9 and 18.9%, for sliding and 24.7 and 24.2% for rolling, respectively. The results also make it clear that in comparison to gold, there is an increase in the type of particle movement; in case of gold, the particles with radiuses larger than 480 nm starts to rolling before sliding, while for DNA it happens for particles with radiuses larger than 530 nm. The comparison between three important contact theories (JKR, DMT and Hertz) shows that there is a small difference between the critical times and forces of them.
Keywords:
Nano-manipulation, Pushing, Dynamic Model, DNA Molecules, Atomic Force Microscopy
1. Introduction
The continual interest in controlling and achieving more perceptive comprehension in prominent biological systems for biomedical investigations, the industry and the biomaterial researchers requires the use of techniques that allow the manipulation of biological samples with minimal or no intrinsic natural structural damage. Advances in micro and nanotechnology revealed that numerous manipulation techniques for imaging, monitoring and characterization of biological matters can be employed in an accurately controlled way. Amongst the techniques accessible to biologists, AFM can manipulate structures with the highest precision. AFM allows the study of the mechanical properties of biological structures in on the micro and nanoscales. Alterations in the mechanical properties of individual cells reflect their physiological state, which can help clarify pathological states, for example cancer. In this way intact cells could be well distinguished from cancerous ones.[1] The direct investigation of single molecule mechanical properties - single molecule force spectroscopy - has been accomplished by respective methods. The breakthrough for the AFM in this area was achieved in 1994 by generation of a one-dimensional vertical pulling AFM. This apparatus enabled the observation of a single streptavidin-biotin complex bond rupture[2]. The new method called AFM Force Spectroscopy used the cantilever tip to pick up and pull at single molecules - most significantly polymers. By applying the high vertical force resolution of the AFM, force-distance curves could be developed which delineate the mechanical tension on an individual polymer with respect to the pulling distance.[3] The applications for single molecule AFM force spectroscopy progress manifold scientific expertise, ranging from material science to biology. AFM can be used not only for mechanical imaging but also for nanometer level mechanical manipulation of biological samples by applying its capability of compressing and stretching them with a sharp tip mounted on a thin cantilever.[4] The recent interest in single molecule visualization of DNA in flow is driven by at least one principle: these visualizations, typically conducted in association with description of the motion is obtained from a molecular dynamic simulation/model, ensures the opportunity to understand the profound dynamics of polymers in flow as well as to approve or abolish existing theories and to create coherent ones. Therefore, over the last decade, the study of DNA dynamics in flow has played a pivotal role in understanding the rheology of dilute polymer solutions.[5] With the advent of analytical ultracentrifugation in the mid-1920s, researchers had the choice of using either a sphere (Stokes equation) or an ellipsoid (Perrin equations) to represent molecules in solution. This restricted menu was later augmented by "subunit" modeling techniques in which spherical subunits were used to build up the whole molecular structure.[6] Using the tapping mode of AFM imaging, compression elasticity of single double-stranded DNA (dsDNA) molecules in the force region was evaluated. With images under ambient conditions, Young’s moduli of dsDNA in compression were calculated.[7] Recent improvements in single DNA manipulation with AFM have proved its capability in analyzing genetic information at the molecular level. Long et al. established an optimized DNA manipulation method in which an accurate and efficient method for DNA manipulation in different ways such as dissection, folding and picking were realized. This method made a great progress in high-efficiency nanomanipulation of small molecules with complex structures, and also provides the possibility to understand the intrinsic properties of single biomolecules deeply.[8] The first model for the pushing of nanoparticles was presented by Falvo, where surface forces were ignored. Sitti and Hashimoto considered the surface forces by using the Johnson–Kendall–Robert theory (JKR), and proposed a new model for the tele-operated nanoparticle pushing process.[9] Korayem and Zakeri investigated the manipulation models and developed a model for the sensitivity analysis of particle pushing in critical conditions.[10] Obtaining a characterizing model has also been studied in various researches. Korayem et al. also considered the liquid environment condition on a nano scale. Some of the newly discovered effects such as the viscous drag force on both sides of the cantilever and the relevant local surface tension of cantilever at the air/liquid interface were added to the dynamic model of manipulation in air. These forces, which are applied on the cantilever, were extracted and the new dynamic model was obtained for the manipulation of the submerged nanoparticles in liquid environment[11].This article aims at studying the manipulation dynamics of DNA nanoparticles in biological liquid by means of the theoretical force analysis, and to compare it to the pushing of nanoparticles in liquid and air. The ultimate goal is to propose an accurate model for the pushing of biological nanoparticles, which could be applied for the assembly of nano/micro objects. The pull-off forces are modeled by means of the JKR contact mechanics model. First the process is simulated for a 50-nm radius nanoparticle in Ethanol, and then the critical times and forces are analyzed for different radiuses of nanoparticle. The simulation results are compared with the results of previous studies in liquid. Finally the results of JKR theory are compared to the ones related to Hertz and DMT theories.
2. Theory
In nano manipulation process, the probe is considered as a spherical shape. A view of the contact forces between probe and cantilever and between probe and nanoparticle and also forces applied on the cantilever and the probe can be seen in Figure 1.In this part the used formulas in Mathematica code are shown. Dynamic equations are developed based on the free body diagram of pushing system, including AFM cantilever and probe, nano-particle and substrate. The equations are derived from writing the existing forces in 2 directions. (y and z) The total force (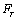 ) and its angle (
) and its angle (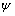 ) are finally calculated using these formulas. In this formula,
) are finally calculated using these formulas. In this formula, 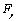 and
and 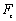 , are bending forces of cantilever.
, are bending forces of cantilever. 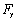 and
and 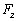 are vertical and horizontal forces of the probe tip and
are vertical and horizontal forces of the probe tip and 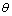 is the torsion angle of cantilever.
is the torsion angle of cantilever. 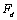 is the drag force and
is the drag force and 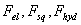 are electrostatic force, squeeze film force and hydration force respectively.
are electrostatic force, squeeze film force and hydration force respectively.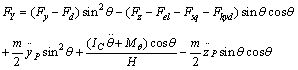 | (1) |
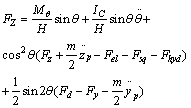 | (2) |
Finally pushing force and angle of applying probe force are calculated using the following equations:[11]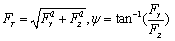 | (3) |
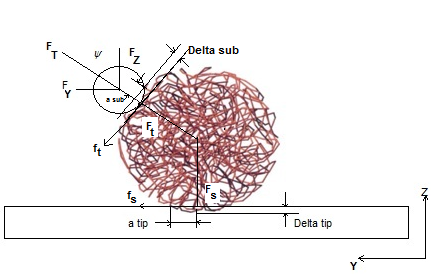 | Figure 1. Interaction forces and contact deformations between tip/particle and particle/substrate for DNA packing |
In order to start the sliding and rolling movements, the total force should overcome the sliding and rolling friction forces. For the nanoparticle sliding on the substrate: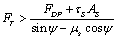 | (4) |
And for the nanoparticle rolling on the substrate:[11]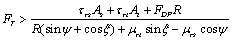 | (5) |
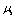 is Sliding friction coefficient and
is Sliding friction coefficient and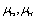 are rolling friction coefficients of sample and tip. Also
are rolling friction coefficients of sample and tip. Also 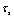 is shear strength of contact area in the sliding and
is shear strength of contact area in the sliding and 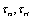 are shear strength of contact areas in the rolling operation related to sample and tip respectively.
are shear strength of contact areas in the rolling operation related to sample and tip respectively. 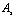 and
and 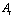 are the contact areas of sample and tip.
are the contact areas of sample and tip.
3. Simulation Assumptions
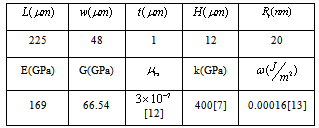
In order to make the possibility of comparing the results of simulations to the recent works in liquid environments, the initial data are assumed to be the same as the previous researches. The simulation of the problem’s equations is considered by means of the previously developed algorithm by Korayem et al. 2011.In order to simplify the simulation, the hypothesis of a spherical shape object has been used and it is imagined that a group of DNA molecules shaped a spherical object. This assumption was used by Arsuagaa et al. 2002[15].Table 1. AFM geometric constants and mechanical properties
 |
| |
|
The AFM geometric constants and mechanical properties are shown in Table 1. These are the standard values which are usually used for simulating the AFM work process. L, t and W are Length, thickness and width of the cantilever and H is the probe height. Also 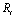 is the tip radius. E and G are Young and Shear modulus and
is the tip radius. E and G are Young and Shear modulus and 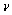 is Poisson’s coefficient.
is Poisson’s coefficient.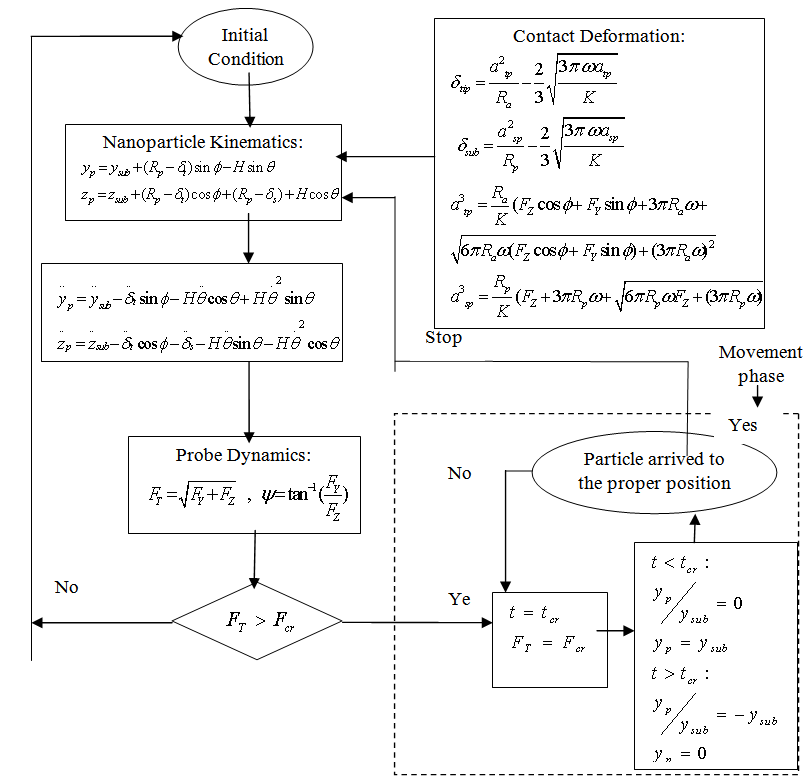 | Figure 2. Flow chart of dynamic modeling simulation |
The used properties of DNA are also shown on Table 1. 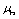 is the rolling friction coefficient of sample and
is the rolling friction coefficient of sample and 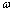 is work of adhesion. K is the reduced elasticity modulus between two contacted materials which is calculated by using the following formula.
is work of adhesion. K is the reduced elasticity modulus between two contacted materials which is calculated by using the following formula.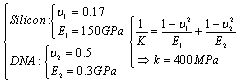 | (6) |
Assuming a substrate velocity of 100 nm/s the initial conditions are obtained by simplifying the equations at t = 0.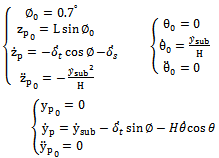 | (7) |
4. Simulation Results
In this part, different diagrams of simulation process are shown. The diagrams have been compared to the ones who are related to the manipulation process of gold nanoparticle and the justifications are made based on the differences between gold and DNA. Figure 3 demonstrates the critical conditions of motion for the DNA and gold particle of 50 nm radius during the pushing process. The medium is considered to be ‘‘Ethanol’’ in case of DNA. It can be seen that the intersections for both rolling and sliding resistance forces are larger in case of DNA. It is also clear that these critical intersections happen later for DNA. For a nanoparticle with a 50 nanometer radius, the critical sliding force is smaller than the critical rolling force. In other words, for a particle in this size, the total force will overcome to the sliding resistance sooner than rolling resistance and rolling motion happens first. This phenomenon could be different for larger particles and it will be investigated in next diagrams.| Table 2. The intersection amounts for rolling and sliding time and force |
| | Results | Gold | DNA | Increase(%) | | Rolling time | 338 msec | 420 msec | 24.2 | | Rolling force | 0.834 μN | 1.04 μN | 24.7 | | Sliding time | 227 msec | 270 msec | 18.9 | | Sliding force | 0.67 μN | 0.79μN | 17.9 |
|
|
Table 2 shows the critical time and force needed for manipulation of gold and DNA nanoparticles respectively. In this table the comparison can be made easier and it is obvious that more force and time are needed to start the manipulation process for DNA particle than a gold particle.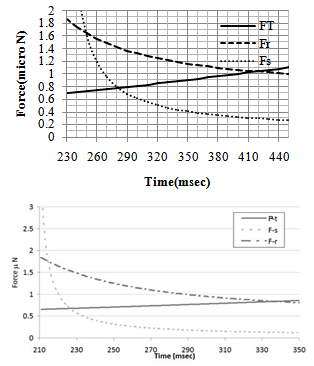 | Figure 3. Critical conditions of motion for: A. the DNA particle and B. the gold particle[11] |
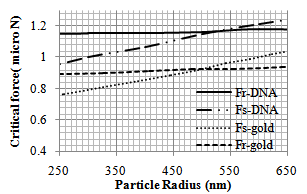 | Figure 4. Variation of critical force (Fcr) of pushing for different gold[11] and DNA particle radii |
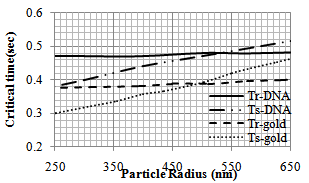 | Figure 5. Variation of critical time (tcr) of pushing for different gold[11] and DNA particle radii |
In order to observe the dynamic behavior and the type of movement of the nanoparticle (rolling or sliding), the simulation has been done for different radiuses of nanoparticle (from 50 to 1000 nm). So the effect of radius size of the particle on pushing critical force and time is clear. As shown in diagrams of the Figures 4 and 5, for pushing in problem conditions, the nanoparticles with radius smaller than about 530 nm start to slide before rolling while those with larger radiuses, first start to roll on the substrate. The results show that in comparison with the gold manipulation, this result happens in larger nanoparticles and it has an increase; because for pushing gold nanoparticles, the change in the process happens after 480 nm.In the next part, different liquids are considered as the environment. Three biological liquids (ethanol, methanol and blood) have been used and their used properties in the simulation are shown in table 3.The comparison has been done between the three conditions in the figures 6 and 7. For blood with a bigger viscosity than ethanol, the critical sliding and rolling forces are larger and in case of methanol with a smaller viscosity, these forces are smaller than ethanol. So it can be seen that viscosity has a more significant effect than tension surface.| Table 3. Properties of biological liquids |
| | Ethanol | Methanol | Blood | | Viscosity | 0.0012 | 0.000544 | 0.003 | | Tension surface | 0.0226 | 0.0221 | 0.05589 |
|
|
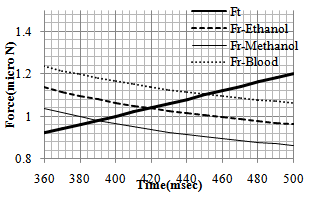 | Figure 6. Rolling resistance force for 3 different liquid environment |
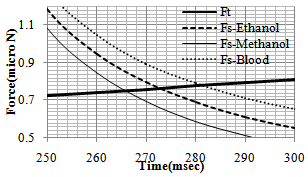 | Figure 7. Sliding resistance force for 3 different liquid environment |
In order to investigate the effect of contact theory which is used in the process on the critical time and force, the simulation has been done for three major contact models: Hertz, JKR and DMT. Results are shown in Figure 8 and Table 4 shows the comparison between them. It can be seen that there is a negligible difference between the critical times and forces of these theories. In other words, in this part it has been proved that in the present work the contact theory does not have a significant effect on the results and choosing each of them will give almost the same amounts. So for the future works, choosing each of them is allowed and will not affect the results greatly.Figure 9 and 10 show the increase of Contact depth and Contact radius between tip and particle, during the static phase of the process for the three theories which are a proof that there is no sliding between the tip and the particle. They also show that there is a small difference between these theories.| Table 4. Critical rolling and sliding time and force for Hertz, JKR and DMT theories |
| | | Critical rolling force | Critical sliding force | Critical rolling time | Critical sliding time | | JKR | 1.041 | 0.77 | 0.45 | 0.3 | | Hertz | 1.03 | 0.76 | 0.43 | 0.28 | | DMT | 1.035 | 0.76 | 0.44 | 0.29 |
|
|
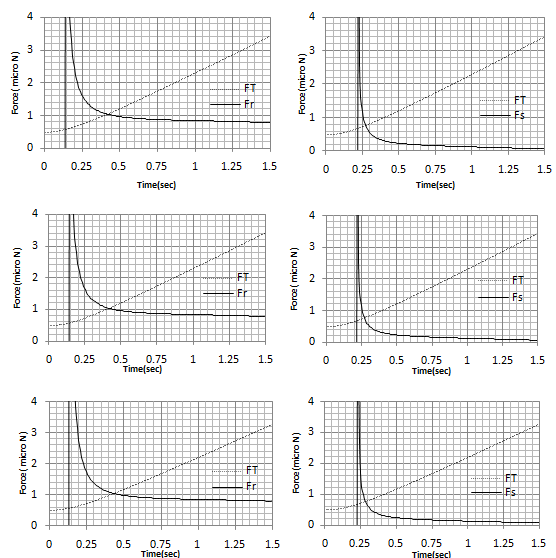 | Figure 8. Critical sliding and rolling force and time for A. JKR theory B. Hertz theory C. DMT theory |
5. Discussion and Conclusions
In this paper, nano manipulation of the DNA nano particles has been investigated in fluid environmental conditions. The manipulation process is simulated for nanoparticles of different radiuses (from 50 to 1000 nm). In addition, the manipulation process is simulated for nanoparticles of 50 nm radius submerged in ethanol and for a cantilever that is half-submerged in liquid. The required critical force and time for the manipulation of DNA nanoparticle show an increase over the existing values for manipulation of gold nanoparticle. This was predictable due to the larger elasticity modulus and smaller adhesion energy of DNA in comparison to gold. As the size of the nanoparticle increases and becomes closer to micro world, it starts to roll before sliding, while for nanoparticles with radiuses smaller than 500 nm, the sliding happens before rolling. It is also clear that the needed force and time for starting the process became larger by increasing the radius of the nanoparticle. The comparison between three contact models (Hertz, JKR and DMT) shows that there is not a significant difference between using them and they all show almost the same results. Increasing the depth and contact radius during the process shows that there is no sliding between probe and nanoparticles so manipulation can be done successfully. It can be seen also that there is a small difference between the depth and contact radius for three contact theories, so it is another proof for close results of these theories.Finally, it should be mentioned that for an accurate nanoparticle manipulation in liquid media, more studies are needed, considering various intermolecular forces that are involved in different situations. Future works in this area could be the simulation of manipulation process for other biological cells using AFM. Also an experimental work for verification of this simulation seems to be necessary.
References
| [1] | Castillo, J., Dimaki M. and Svendsen W.E., "Manipulation of biological samples using micro and nano techniques", 2009, Integr. Biol., 1, p.30–42 |
| [2] | Lee, G., Kidwell D.A., and Colton R.J., "Sensing Discrete Streptavidin-Biotin Interactions with Atomic Force Microscopy". 1994, Langmuir,. 10(2): p. 354-7. |
| [3] | Hugel, T. and Seitz M., "The study of molecular interactions by AFM force spectroscopy." 2001, Macromolecular Rapid Communications,. 22(13): p. 989-1016. |
| [4] | Afrin,R., Zohora U.S., Uehara H., Watanabe-Nakayama T. and Ikai A., "Atomic force microscopy for cellular level manipulation: imaging intracellular structures and DNA delivery through a membrane hole", 2009, J. Mol. Recognit; 22: p.363–372 |
| [5] | Larson R.G., "The rheology of dilute solutions of flexible polymers: progress and problems", 2005, J. Rheol. 49, p.1–70. |
| [6] | Charles H., "Estimating Friction Coefficients of Mixed Globular/Chain Molecules, such as Protein/DNA Complexes", 1995, Biophysical Journal Vol. 69 September p.840-848 |
| [7] | Yi L., XinCheng Sh., Jing W., Lei B., ZhiLing Z. & DaiWen P., "Measuring radial Young’s modulus of DNA by tapping mode AFM", 2007 Chinese Science Bulletin, vol. 52,no. 23, p.3189-3192 |
| [8] | Long F., Wang C., Lu M., Zhang F., Sun J., Hu J.,"Optimizing single DNA molecules manipulation by AFM", Journal of Microscopy, 2011,Volume 243, Issue 2, pages 118–120 |
| [9] | Sitti M, Hashimoto H," Force controlled pushing of nanoparticles: modeling and experiments." 2000.IEEE/ASME Trans Mechatron 5:p.199–211 |
| [10] | Korayem M.H., Zakeri M, "Sensitivity analysis of nanoparticles pushing critical conditions in 2-D controlled nanomanipulation based on AFM", 2009. J Adv Manuf Technol 41:p.714–726 |
| [11] | Korayem M. H., Motaghi A., Zakeri M., "Dynamic modeling of submerged nanoparticle pushing based on atomic force microscopy in liquid medium", 2011, J Nanopart Res, Vol. 13, No. 10, p. 5009-5019. |
| [12] | Ku¨hner F., Erdmann M., Sonnenberg L., Serr A., Morfill J., and Gaub H, Langmuir A., "Friction of Single Polymers at Surfaces", 2006, 22, p.11180-11186 |
| [13] | Yi L., XinCheng Sh., JingJing W., Lei B., ZhiLing Z. & DaiWen P., "Discrimination of DNA Hybridization Using Chemical Force Microscopy", 1999, X,Biophysical Journal Vol. 76 June, p.2922–2933 |
| [14] | Beard J.D., Gordeev and S.N., Guy R.H., "AFM Nanotools for Surgery of Biological Cells", 2011, Journal of Physics: Conference Series 286, 012003 |
| [15] | Arsuagaa J., Tanb R. K.-Z., Vazqueza M., Sumnersa D.W., Harveyb S. C.,"Investigation of viral DNA packaging using molecular mechanics Models", Biophysical Chemistry 101 –102 (2002) 475–484 |

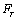 ) and its angle (
) and its angle (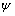 ) are finally calculated using these formulas. In this formula,
) are finally calculated using these formulas. In this formula, 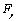 and
and 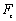 , are bending forces of cantilever.
, are bending forces of cantilever. 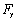 and
and 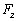 are vertical and horizontal forces of the probe tip and
are vertical and horizontal forces of the probe tip and 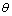 is the torsion angle of cantilever.
is the torsion angle of cantilever. 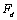 is the drag force and
is the drag force and 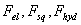 are electrostatic force, squeeze film force and hydration force respectively.
are electrostatic force, squeeze film force and hydration force respectively.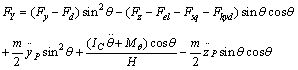
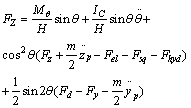
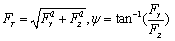

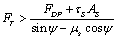
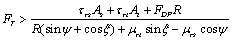
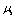 is Sliding friction coefficient and
is Sliding friction coefficient and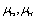 are rolling friction coefficients of sample and tip. Also
are rolling friction coefficients of sample and tip. Also 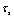 is shear strength of contact area in the sliding and
is shear strength of contact area in the sliding and 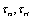 are shear strength of contact areas in the rolling operation related to sample and tip respectively.
are shear strength of contact areas in the rolling operation related to sample and tip respectively. 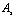 and
and 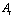 are the contact areas of sample and tip.
are the contact areas of sample and tip.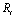 is the tip radius. E and G are Young and Shear modulus and
is the tip radius. E and G are Young and Shear modulus and 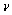 is Poisson’s coefficient.
is Poisson’s coefficient.
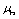 is the rolling friction coefficient of sample and
is the rolling friction coefficient of sample and 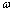 is work of adhesion. K is the reduced elasticity modulus between two contacted materials which is calculated by using the following formula.
is work of adhesion. K is the reduced elasticity modulus between two contacted materials which is calculated by using the following formula.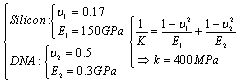
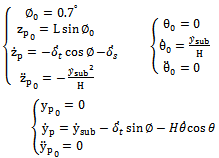






 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML