M. H. Korayem, Z. Rastegar, M. Taheri
Robotic Research Laboratory, Center of Excellence in Experimental Solid Mechanics and Dynamics, School of Mechanical Engineering, Iran University of Science and Technology, Tehran, 16846-13114, Iran
Correspondence to: M. H. Korayem, Robotic Research Laboratory, Center of Excellence in Experimental Solid Mechanics and Dynamics, School of Mechanical Engineering, Iran University of Science and Technology, Tehran, 16846-13114, Iran.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Application of four nano-contact mechanics models, JKR, DMT, Hertz and PT in manipulation of biological cells in biological environment based on atomic force microscope has been analyzed, and the sensitive and non-sensitive parameters and their sensitive ranges have been identified. To analyze sensitivity of contact theories to basic parameters of biological cell, the Sobol method was used. All the used models are small deformation contact mechanics models, but they are different in considerations and limitations. This selection was on purpose to analyze and compare theoretical and empirical models sensitivities. The results indicate that the deformation of biological nano-particle is very sensitive to the elasticity modulus in all models. Adhesion energy, Poisson ratio and particle radius have, respectively, the next ranks which the results of graphic SA confirm, but their effects are not the same in different models. Moreover, the results of the graphic sensitivity analysis SA show that the degree of sensitivity depends on the apparent values of input parameters, such that by changing the magnitude of a specific parameter, it could be possible to increase or decrease the sensitivity.
Keywords:
Nano-contact mechanics models, Sensitivity analysis, Manipulation
1. Introduction
Sensitivity analysis (SA) is the study of how the uncertainty in the output of a model (numerical or otherwise) can be apportioned to different sources of uncertainty in the model input[1]. A related practice is 'uncertainty analysis' which focuses rather on quantifying uncertainty in model output. Ideally, uncertainty and sensitivity analysis should be run in tandem. Sensitivity analysis can be useful to computer modelers for a range of purposes[2] including:● Support decision making or the development of recommendations for decision makers (e.g. testing the robustness of a result);● Enhancing communication from modelers to decision makers (e.g. by making recommendations more credible, understandable, compelling or persuasive);● Increased understanding or quantification of the system (e.g. understanding relationships between input and output variables); and● Model development (e.g. searching for errors in the model).Sensitivity analysis can be used● To simplify models● To investigate the robustness of the model predictions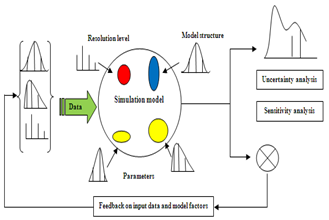 | Figure 1. Ideal scheme of a possibly sampling-based sensitivity analysis |
● To play what-if analysis exploring the impact of varying input assumptions and scenarios● As an element of quality assurance (unexpected factors sensitivities may be associated to coding errors or misspecifications).It provides as well information on:● Factors that mostly contribute to the output variability● The region in the space of input factors for which the model output is either maximum or minimum or within pre-defined bounds (see Monte Carlo filtering above)● Optimal; or instability; regions within the space of factors for use in a subsequent calibration study● Interaction between factorsDespite sensitivity analysis (SA) benefits and usages, its application has been rarely studied in manipulation of biological cell. Sensitivity analysis has been used widely to analyze models in other sciences, but to our knowledge this type of analysis has not been used extensively for the analysis of contact mechanics models. The SA results will be extremely important for adjusting the force applied to the nano-particles and the duration of manipulation and for selecting the appropriate instrument for the accurate planning of fabrication and assembly of nanoobjects. Manipulation and assembly of nano-particles have garnered widespread interest for the last few years, and nano-object manipulation based on AFM is one of the important means for building miniaturized systems and machines[3]. However, few studies have focused on its modeling and applications in motion analysis and planning. Using AFM probe as a manipulation tool enables precise positioning particle for micro/nano-assembly[4], which is the base of accurate control of nano-particles positioning and assemblies. The most important part of manipulation is the contact moment in which pushing force leads to deformation in nano-particle. In previous studies include the works done by Korayem et al. sensitivity of critical parameters in AFM- based nano- manipulation, including the nano-particle pushing force and time versus changing all parameters of the nano- manipulation process has been investigated[5]. The presented model included both adhesional and normal friction forces. Also, pull-off forces are modeled by using the Johnson– Kendall–Roberts (JKR) contact mechanics model. The dynamic model of the nano-particles pushing on a substrate based on the atomic force microscope with a rectangular cantilever (RC) and a V-shaped cantilever (VSC), which includes 12 nonlinear and coupled equations, has been analyzed, by using the graphical and automatic differential sensitivity analysis (SA) methods, and the sensitive and non-sensitive parameters and their sensitive ranges have been identified[6]. Different contact mechanics models have been applied to manipulation of nano-particles and biological cells. Although the basis of manipulation in both nano-particle and biological cell is the same, but there are some differences and limitations which make manipulation of biological cells more challenging. Since biological cells are softer, their manipulation especially at contact moment needs more care because extra applied forces may result in large unwanted deformations even lead to cell damage and destruction. Beside, biological cell manipulation is done in biological environment which is liquid, so there are interaction forces, such as Van der Waals and hydration forcea, which should be considered in this process. Adhesion energy difference between nano-particle and biological cell is approximately significant so it can change contact condition. In this paper four contact mechanics models have been chosen to be analyzed. The first model which is studied is the Hertz theory which does not consider adhesion energy. JKR and DMT theories are two other models studied as the extended versions of Hertz theory, which consider adhesion energy. And the last model is PT which is going to be analyzed as an empirical model.
2. Theory
Microscopes have always been one of the essential instruments for research in the biomedical field. Radiation- based microscopes (such as the light microscope and the electron microscope) have become trustworthy companions in the laboratory and have contributed greatly to our scientific knowledge. However, although digital techniques in recent years have still enhanced their performance, the limits of their inherent capabilities have been progressively reached. The advent of scanning probe microscopes and especially of the atomic force microscope (AFM) has opened new perspectives in the investigation of biomedical specimens and induces to look again with rejuvenated excitement at what we can learn by “looking” at our samples.AFM images show significant information about surface features with unprecedented clarity. The AFM can examine any sufficiently rigid surface either in air or with the specimen immersed in a liquid. Recently developed instruments can allow temperature control of the sample, can be equipped with a closed chamber for environmental control, and can be mounted on an inverted microscope for simultaneous imaging through advanced optical techniques.The field of view can vary from the atomic and molecular scale up to sizes larger than 125 µm so that data can be compared with other information obtained with lower resolution techniques. The AFM can also examine rough surfaces because its vertical range can be up to 8–10 µm. Large samples can be fitted directly in the microscope without cutting. With stand-alone instruments, any area on flat or nearly flat specimens can be investigated. In addition to its superior resolution with respect to optical microscopes, the AFM has these key advantages with respect to electron microscopes. Compared with the scanning electron microscope (SEM), the AFM provides superior topographic contrast, in addition to direct measurements of surface features providing quantitative height information[7].One of the main reasons for the success of AFM in biomedical investigations is its ability to scan samples in physiological condition, that is, immersed in liquid solutions. But during manipulation, contact forces cause to indentation on contact surfaces, which is considerable in nano-scale and affects the manipulation processes. Several models like Hertz, Johnson– Kendall–Roberts (JKR), Derjaguin– Muller–Toporov (DMT), Maugis–Dugdale (MD) have been utilized as the continuum mechanics approaches in nano- scale[8]. The Hertzian adhesion force, which treats rigid bodies, has been extended to deformable bodies by Johnson, Kendall, and Robert. Their JKR theory starts by defining the elastic modulus of the two spheres. Figure 2 shows the schematic free body diagram which indicates the interaction between an AFM probe tip and a nanoparticle. Contact forces required to separate the surfaces are mainly proportional to the equivalent radius and adhesion energy between the contacting surfaces. The normal force Ft and Fs in contact area, would deform the particle with a contact radius of a.Contact mechanics models are used in different literature, but since these models have been developed for especial conditions their application in other situation would encounter problems and limitations. The Hertz model is the first contact mechanics model which does not consider the surface forces in contact, so if surface forces presents, this model is not appropriate for low loads. DMT theory considers a long-ranged surface force which acts outside the radius of the circle of contact, but contact geometry is similar to Hertzian. This model applies to rigid system with low λ, low adhesion and small radii of curvature, but may underestimate the true contact area. JKR considers a short-ranged surface force which acts inside the radius of the circle of contact. It applies to high λ systems, high adhesion and large radii of curvature, but may underestimate loading. Other important contact mechanics model is MD theory which considers the Dugdale potential to describe attractive forces. It has analytical solution, but parametric equations. It applies to all system with all values of λ. But since this model is hard to use in complex system, other empirical and semi- empirical models such as BCP, COS, PT and SUN are developed to enhance the tractability of the MD model[9].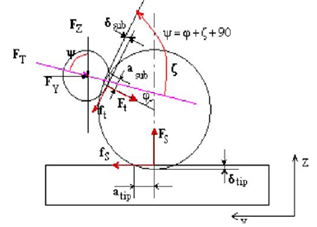 | Figure 2. Interaction forces and the resultant deformations between tip/ particle and particle/substrate[5] |
Forces required to separate two surfaces are mainly proportional to the equivalent radius and adhesion energy between contacting surfaces.
2.1 Contact mechanics Models
Hertz theoryThe pioneering work on contact mechanics topic was performed by Hertz in 19th century[10]. He solved the contact mechanics problem for two spheres of radius R1 and R2 assuming only elastic deformation of the materials, thus there is no interpenetration of the surfaces, and no attractive forces acting between the surfaces, the interaction force is sketched in Figure 3. The spheres are actually treated as paraboloids with curvature radii R1 and R2 respectively, which is a valid approximation if the contact radius is much less than the curvature radii. The symmetry of the problem leads to a flat, circular contact area between the materials when they are pushed together. 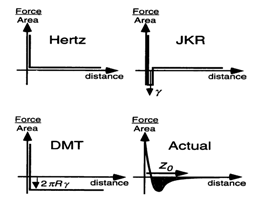 | Figure 3. Interaction forces (normalized per unit area) for Hertz, JKR and DMT models compared to a realistic interaction[9] |
His result leads to the following relationships: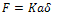 | (1) |
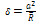 | (2) |
Contact radius and adhesion force are obtained as follows: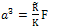 | (3) |
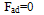 | (4) |
Where, F is the normal force in contact area, 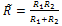 is effective radius of two contacted surfaces of radius R1 and R2. K is the reduced elastic modulus, and is obtained from following equation:
is effective radius of two contacted surfaces of radius R1 and R2. K is the reduced elastic modulus, and is obtained from following equation: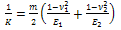 | (5) |
Where m is a constant parameter depending on the tip geometry (m=1 for cylindrical, m=1.5 for spherical. and m=2 for the conical shapes), E1 and E2 are young’s modules, v1 and v2 are poison’s coefficients, respectively, and ω =2γ is the work of adhesion. The surface energy γ is related to the energy required to separate two flat surfaces from contact to infinity and for two contacted surfaces is equal to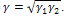 JKR theoryThe Hertzian model does not take in to account attractive forces between the contacting surfaces. The Johnson- Kendall-Roberts (JKR) theory considers the effect of finite surface energy. In particular, the theory calculated the increase in contact area that results from elastic bodies deforming to accommodate their mutual attraction, so that the deformations are no longer perfectly Hertzian. As with the Hertz theory, the JKR theory applies to the case of two spheres in contact. The model can be extended to more general shapes.The interface is considered to possess an energy per unit area
JKR theoryThe Hertzian model does not take in to account attractive forces between the contacting surfaces. The Johnson- Kendall-Roberts (JKR) theory considers the effect of finite surface energy. In particular, the theory calculated the increase in contact area that results from elastic bodies deforming to accommodate their mutual attraction, so that the deformations are no longer perfectly Hertzian. As with the Hertz theory, the JKR theory applies to the case of two spheres in contact. The model can be extended to more general shapes.The interface is considered to possess an energy per unit area 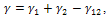 where γ1 and γ2 are the respective surface energies and γ12 the interfacial energy. γ is equivalent to the Dupre energy of adhesion which corresponds to the work per unit area required to separate the surfaces from contact to infinity. As such, the parameter γ effectively encompasses all attractive interaction forces. However, the JKR approximation assumes that all the interaction forces have zero range. In other words, the surfaces gain an energy per unit area γ if they touch, but not if they are separated by an infinitesimal amount or more.The equations are as follows[11]:
where γ1 and γ2 are the respective surface energies and γ12 the interfacial energy. γ is equivalent to the Dupre energy of adhesion which corresponds to the work per unit area required to separate the surfaces from contact to infinity. As such, the parameter γ effectively encompasses all attractive interaction forces. However, the JKR approximation assumes that all the interaction forces have zero range. In other words, the surfaces gain an energy per unit area γ if they touch, but not if they are separated by an infinitesimal amount or more.The equations are as follows[11]: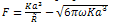 | (6) |
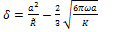 | (7) |
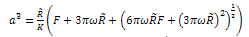 | (8) |
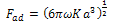 | (9) |
Calculated surface energy for pure water is about 0.00013 J/m2 so the adhesion energy will be 0.00026 J/m2. This adhesion energy is used forJKR, DMT and PT models.DMT theoryThe problem of contact mechanics in presence of adhesion is treated by a significantly different approach by Derjaguin, Muller and Toporov (DMT). Unlike the JKR case, the DMT theory assumes that the shape of contact is not affected by the interfacial forces. Rather, the overall Hertzian deformation profile is maintained, but the contact area is increased.The equations are given as: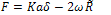 | (10) |
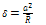 | (11) |
Contact radius and adhesion force are obtained as follows: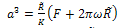 | (12) |
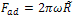 | (13) |
PT theoryThe COS and PT equations provide the means to effectively apply the MD model to experimental data but the COS and PT models have more rapid calculations than the MD analytical model. The equations are[12]: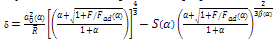 | (14) |
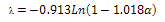 | (15) |
In which: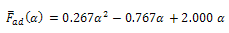 | (17) |
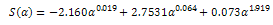 | (18) |
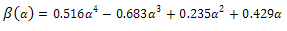 | (19) |
To use these equation for biological cell in biological environment, some modifications are needed. one of the most important parameters which is going to be different for biological environment is adhesion energy.In these equations γ tands for surface energy which is related to ω with the following equation: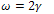 | (20) |
To calculate surface energy for biological cell/ AFM tip contact in pure water, equivalent Hamaker constant is needed which is obtained as follows: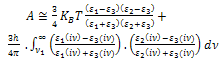 | (21) |
Where, KB is Boltzman coefficient. T is temperature in Kelvin. ε1 , ε2 and ε3 are, respectively, dielectric constants for tip, sample and environment. The second part of the equation can be omitted.Considering seperation distance equivalent to 0.165 nm, surface energy will be as follows: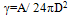 | (22) |
In which A is Hamaker constant.Other modifications include interaction forces such as Van der Waals, Electrical double layer force and Hydration force, which are going to be added to external force.
3. SA Results
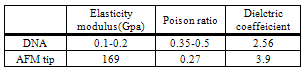
Deformation sensitivity to four major parameter; particle radius, Poison’s ratio, elasticity modulus and adhesion energy of particle; were analyzed. Equations of models were obtained for costant pushing force. To show deformation sensitivity percentage, sobol method were used and results presented. Table 1 shows constant parameters used in this analysis.Table 1. DNA and AFM tip properties[13,14]
 |
| |
|
Rupture force of DNA is considered as a constant applied force which is in pN range[13,15].Figure 4(a) shows deformation versus particle radius for constant force in Hertz model. As it shown, increasing of particle radius leads to small and linear growth of deformation.The same reults obtained for JKR, DMT and PT model (Fig.4(b-d)). These curves show that particle radius does not play an important role in deformation depth of particle, which confirm that the deformation is not so sensitive to size of the particle. Biological cells radius range between nano and micrometer which is the wide range. In this analysis DNA has been chosen as the base which radius is in nano-meter range therefore the same range have been used for analysis in order to decrease errors and dispersion. These data are not related to one especial cell so they cannot form a solid curve, but the behavior of the cell toward selected data can form approximate relationship between deformation and parameters. 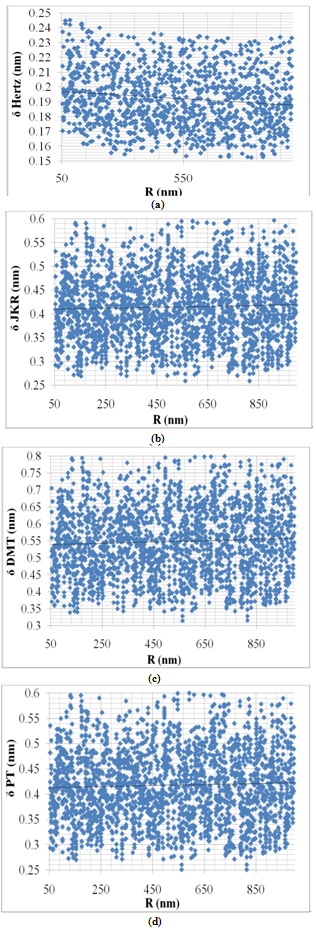 | Figure 4. Variation of deformation vs. particle radius for Hertz, JKR, DMT and PT contact mechanics models |
Figure 5 shows deformation variation versus Poison’s ratio for Hertz, JKR, DMT and PT models. These curves indicate that increasing of Poison’s ratio results in decreasing of deformation, but this increase is approximately linear. The slope of the deformation-Poison’s ratio curve is more than deformation-radius curve which shows that cell’s deformation is more sensitive to Poison’s ratio in comparison with radius. But Poison’s ratio effect is approximately ignorable too.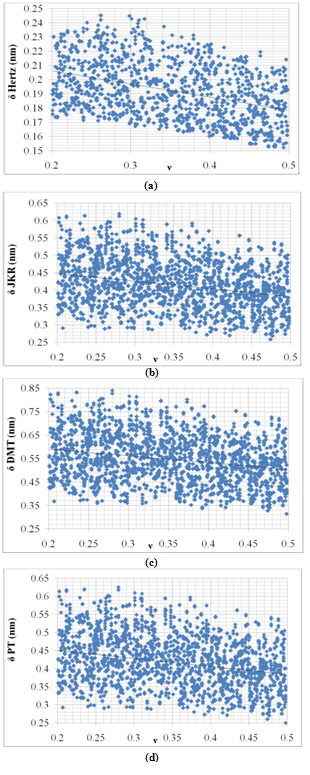 | Figure 5. Variation of deformation vs. Poison’s ratio for Hertz, JKR, DMT and PT contact mechanics models |
Figure 6 shows variation of deformation with increasing of elasticity modulus. Increasing of elasticity modulus leads to decreasing of cell deformation. This result is convinient because particles with higher elasticity modulus are stiffer so the deformation due to applied force will be smaller. Results show that elasticity modulus is more effective parameter in comparison with particle radius and Poison’s ratio. This effect is more clear in Hertz deformation, that is, the slope of Hertz’s curve is sharper than other models.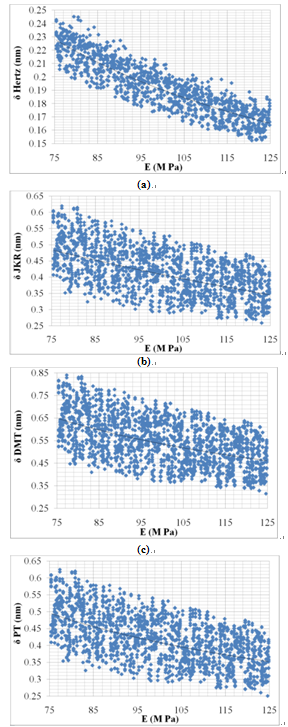 | Figure 6. Variation of deformation vs. elasticity modulus for Hertz, JKR, DMT and PT contact mechanics models |
Figures 7 shows variation of deformation under constant force with increasing of adhesion energy. Hertz contact mechanics model does not consider adhesion energy, so the deformation does not change with adhesion variation which is acceptable. But other models show the most sensitivity to this parameter so their curves have rapid slope, it means increasing of adhesion energy leads to great increase in deformation. This great effect can be explained in this way that when adhesion energy is increased more force is needed to move it and more applied force will lead to more deformation.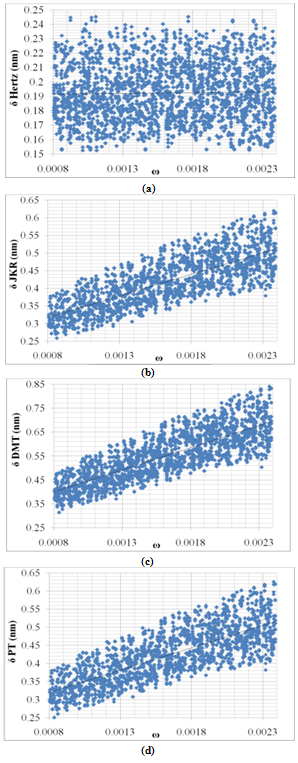 | Figure 7. Variation of deformation vs. adhesion energy for Hertz, JKR, DMT and PT contact mechanics models |
Figures 8-11 show the effect of different parameters on deformation based on sobol sensitivity analysis method. As expected, adhesion energy is the most effective parameter on deformation; except for Hertz theory; and elasticity modulus, Poison’s ratio and particle radius,respectively, are of less importance. Elasticity modulus in Hertz theory has more significant effect. As mentioned before adhesion energy is not considered in Hertz theory so elasticity modulus effect is more visible in graphic analysis. PT and JKR graphic sensitivity analysis show approximately the same behavior of these models toward parameters’ variation but DMT shows more sensitivity to adhesion energy and radius in comparison with those two models.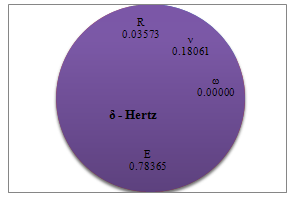 | Figure 8. Percentage of deformation sensitivity to parameters’ variation for Hertz contact mechanics model |
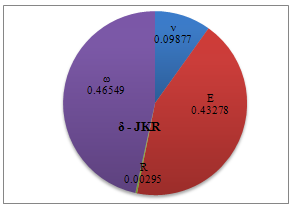 | Figure 9. Percentage of deformation sensitivity to parameters’ variation for JKR contact mechanics model |
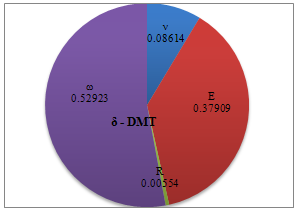 | Figure 10. Percentage of deformation sensitivity to parameters’ variation for DMT contact mechanics model |
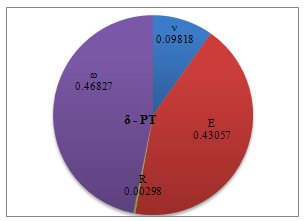 | Figure 11. Percentage of deformation sensitivity to parameters’ variation for PT contact mechanics model |
4. Conclusions and Discussion
This paper simulate four different contact mechanics models in manipulation of biological cell based on AFM and discusses the problem parameter variations’ effect on deformation of biological sample under constant force. It was observed that all of the parameters can affect deformation of nano-particle during nano-manipulation process. Increasing of elasticity modulus leads to decreasing of deformation depth, but except Hertz model which does not consider adhesion energy, PT and JKR models are more sensitive to elasticity modulus in comparison with DMT. In contrast, DMT model shows more sensitivity to adhesion energy than PT and JKR models, however, increasing of adhesion energy in all models, except Hertz theory, results in increasing of deformation depth. Particle radius is the less important parameter in all models and its effect is approximately ignorable, so it can be concluded that the size of particle does not play an important role in choosing appropriate model. Poison’s ratio effect is not significant either, but its effect is more visible in Hertz theory which sensitivity to this parameter is about 20%. Increasing of Poison’s ratio leads to decreasing of deformation depth in all models.Based on simulation results, adhesion energy and elasticity modulus, respectively, are more important in choosing proper model but the size of particle and its Poison’s ratio do not play an important role in this process. Since biological cells have great adhesion energies, if small deformation contact mechanics models are going to be used, DMT must be the most proper one, because it is more sensitive to adhesion energy and biological cells have stronger adhesions that makes their manipulation different from solid nano-particles, although, JKR and PT models can be used either but their sensitivity to adhesion energy is about 6 percent less than DMT. Hertz model cannot be proper to use for live cells, but since fixed biological cells have smaller adhesion energies than live cells, this model can be used for in vitro conditions which use fixed cells in air environment.
References
| [1] | Satelli, A., S. Tarantola, and F. Campolongo, Sensitivity analysis as an ingredient of modelling, Statistical science, 15(4), 377-395, 2000 |
| [2] | Cruz, J. B. and Perkins, W.R, A New Approach to the Sensitivity Problem in Multivariable Feedback System Design, IEEE TAC, Vol. 9, 216-223, 1964. |
| [3] | Jalili N, Laxminarayana K, A review of atomic force microscopy imaging systems: application to molecular metrology and biological sciences. Mechatronics 14:907–945, 2004 |
| [4] | Sitti M, Survey of Nanomanipulation Systems. Proc. of the IEEE-Nanotechnology Conference pp. 75–80, 2001 |
| [5] | M. H. Korayem, M. Zakeri, sensitivity analysis of nanoparticles pushing critical conditions in 2-D controlled nanomanipulation based on AFM, Int J Adv Manuf Technol (2009) 41:714–726 |
| [6] | M.H. Korayem, M. Zakeri, M.M. Aslzaeem, Sensitivity analysis of the nanoparticles on substrates using the atomic force microscope with rectangular and V-shaped cantilevers, Micro & Nano Letters, Vol. 6, Iss. 8, pp. 586–591, 2011 |
| [7] | D. Ricci and P. Carlo Braga, How the Atomic Force Microscope Works, Methods in molecular biology, vol.242, 1-10, 2005 |
| [8] | Johnson KL, Contact Mechanics. Cambridge University, London, 1985 |
| [9] | Kh. Daeinabi, M. H. Korayem, Indentation analysis of nano-particle using nano-contact mechanics models during nano-manipulation based on atomic force microscopy, J Nanopart Res, 13,1075:1091, 2010 |
| [10] | R. W. Carpick, the study of contact, adhesion and friction at the atomic scale by atomic force microscopy, UMI 9828624, 1997 |
| [11] | K. L. Johnson, K. Kendall, A. D. Roberts, Surface Energy and the Contact of Elastic Solids, Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences, Vol. 324, No. 1558 , 301-313, 1971 |
| [12] | Pietrement O, Troyon M, General equations describing elastic indentation depth and normal contact stiffness versus load. J Colloid Interface Sci 226:166–171, 2000 |
| [13] | G. Legaya, E. Finota , R. Meunier-Prestb, M. Cherkaoui- Malkic, N. Latruffec, A. Dereuxa, DNA nanofilm thickness measurement on microarray in air and in liquid using an atomic force microscope, Biosensors and Bioelectronics, 21:627–636, 2005 |
| [14] | J. Israelachvili, H. Weenerstrom, Role of hydration and water structure in biological and colloidal interactions, Nature, 379:219-22, 1996 |
| [15] | C. Bustamante, S. B Smith, J. Liphardt and D. Smith, Single-molecule studies of DNA mechanics, Current Opinion in Structural Biology, 10:279–285, 2000 |




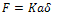
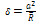
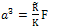
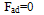
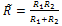 is effective radius of two contacted surfaces of radius R1 and R2. K is the reduced elastic modulus, and is obtained from following equation:
is effective radius of two contacted surfaces of radius R1 and R2. K is the reduced elastic modulus, and is obtained from following equation: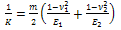
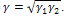 JKR theoryThe Hertzian model does not take in to account attractive forces between the contacting surfaces. The Johnson- Kendall-Roberts (JKR) theory considers the effect of finite surface energy. In particular, the theory calculated the increase in contact area that results from elastic bodies deforming to accommodate their mutual attraction, so that the deformations are no longer perfectly Hertzian. As with the Hertz theory, the JKR theory applies to the case of two spheres in contact. The model can be extended to more general shapes.The interface is considered to possess an energy per unit area
JKR theoryThe Hertzian model does not take in to account attractive forces between the contacting surfaces. The Johnson- Kendall-Roberts (JKR) theory considers the effect of finite surface energy. In particular, the theory calculated the increase in contact area that results from elastic bodies deforming to accommodate their mutual attraction, so that the deformations are no longer perfectly Hertzian. As with the Hertz theory, the JKR theory applies to the case of two spheres in contact. The model can be extended to more general shapes.The interface is considered to possess an energy per unit area 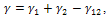 where γ1 and γ2 are the respective surface energies and γ12 the interfacial energy. γ is equivalent to the Dupre energy of adhesion which corresponds to the work per unit area required to separate the surfaces from contact to infinity. As such, the parameter γ effectively encompasses all attractive interaction forces. However, the JKR approximation assumes that all the interaction forces have zero range. In other words, the surfaces gain an energy per unit area γ if they touch, but not if they are separated by an infinitesimal amount or more.The equations are as follows[11]:
where γ1 and γ2 are the respective surface energies and γ12 the interfacial energy. γ is equivalent to the Dupre energy of adhesion which corresponds to the work per unit area required to separate the surfaces from contact to infinity. As such, the parameter γ effectively encompasses all attractive interaction forces. However, the JKR approximation assumes that all the interaction forces have zero range. In other words, the surfaces gain an energy per unit area γ if they touch, but not if they are separated by an infinitesimal amount or more.The equations are as follows[11]: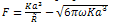
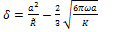
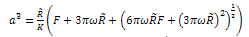
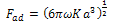
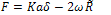
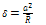
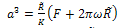
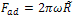
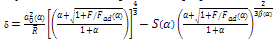
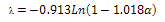
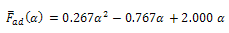
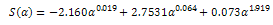
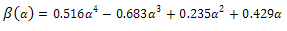
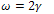
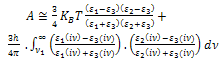
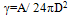








 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML