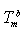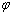| [1] | M. Takagi, “Electron-diffraction study of liquid-solid transition of thin metal films,” Journal of the Physical Society of Japan, vol. 9, pp. 359-363, 1954. |
| [2] | R. Shidpour, H. Delavari H., M. Vossoughi, “Analytical model based on cohesive energy to indicate the edge and corner effects on melting temperature of metallic nanoparticles,” Chemical Physics, vol. 378, pp. 14-18, 2010. |
| [3] | W. Luo, W. Hu, S. Xiao, “Size effect on the thermodynamic properties of silver nanoparticles,” Journal of Physical Chemistry C, vol. 112, pp. 2359-2369, 2008. |
| [4] | L. Grabaek, J. Bohr, E. Johnson, A. Johansen, L. Sarholt-Kristensen, H.H. Andersen, “Superheating and supercooling of lead precipitates in aluminum,” Physical Review Letters, vol. 64, 934-937, 1990. |
| [5] | Q. Jiang, Z. Zhang, J.C. Li, “Superheating of nanocrystals embedded in matrix,” Chemical Physics Letters, vol. 322, pp. 549-552, 2000. |
| [6] | Z. Zhang, J.C. Li, Q. Jiang, “Modelling for size-dependent and dimension-dependent melting of nanocrystals,” Journal of Physics D: Applied Physics, vol. 33, pp. 2653-2656, 2000. |
| [7] | H.W. Sheng, G. Ren, L.M. Peng, Z.Q. Hu, K. Lu, “Epitaxial dependence of the melting behavior of in nanoparticles embedded in Al matrices,” Journal of Materials Research, vol. 12, pp. 119-123, 1997. |
| [8] | H.W. Sheng, G. Ren, L.M. Peng, Z.Q. Hu, K. Lu, “Superheating and melting-point depression of Pb nanoparticles embedded in Al matrices,” Philosophical Magazine Letters, vol. 73, pp. 179-186, 1996. |
| [9] | F.G. Shi, “Size dependent thermal vibrations and melting in nanocrystals,” Journal of Materials Research, vol. 9, pp. 1307-1313, 1994. |
| [10] | H. Saka, Y. Nishikawa, T. Imura, “Melting temperature of In particles in an Al matrix,” Philosophical Magazine A: Physics of Condensed Matter, Structure, Defects and Mechanical Properties, vol. 57, pp. 895-906, 1988. |
| [11] | K. Chattopadhyay, R. Goswami, “Melting and superheating of metals and alloys,” Progress in Materials Science, vol. 42, pp. 287-300, 1997. |
| [12] | H.W. Sheng, K. Lu, E. Ma, “Melting and freezing behavior of embedded nanoparticles in ball-milled Al-10 WT% M (M = In, Sn, Bi, Cd, Pb) mixtures,” Acta Materialia, vol. 46, pp. 5195-5205, 1998. |
| [13] | J. Daeges, H. Gleiter, J.H. Perepezko, “Superheating of metal crystals,” Physics Letters A, vol. 119, pp. 79-82, 1986. |
| [14] | C.J. Rossouw, S.E. Donnelly, “Superheating of small solid-argon bubbles in aluminum,” Physical Review Letters, vol. 55, pp. 2960, 1985. |
| [15] | H. Delavari H, H. Madaah Hosseini, A. Simchi, “A simple model for the size and shape dependent Curie temperature of freestanding Ni and Fe nanoparticles based on the average coordination number and atomic cohesive energy,” Chemical Physics In Press, Corrected Proof, 2011. |
| [16] | H. Omid, H. Delavari H, H.R. Madaah Hosseini, “Melting enthalpy and entropy of freestanding metallic nanoparticles based on cohesive energy and average coordination number,” Journal of Physical Chemistry C, vol. 115, pp. 17310-17313, 2011. |
| [17] | L.-f. Cao, D. Xie, M.-x. Guo, H.S. Park, T. Fujita, “Size and shape effects on Curie temperature of ferromagnetic nanoparticles,” Transactions of Nonferrous Metals Society of China, vol. 17, pp. 1451-1455, 2007. |
| [18] | K.K. Nanda, S.N. Sahu, S.N. Behera, “Liquid-drop model for the size-dependent melting of low-dimensional systems,” Physical Review A - Atomic, Molecular, and Optical Physics, vol. 66, pp. 132081-132088, 2002. |
| [19] | G. Guisbiers, “Size-dependent materials properties towards a universal equation,” Nanoscale Research Letters, vol. 5, pp. 1132, 2010. |
| [20] | G.L. Allen, R.A. Bayles, W.W. Gile, W.A. Jesser, “Small particle melting of pure metals,” Thin Solid Films, vol. 144, pp. 297-308, 1986. |
| [21] | J. Zhong, L.H. Zhang, Z.H. Jin, M.L. Sui, K. Lu, “Superheating of Ag nanoparticles embedded in Ni matrix,” Acta Materialia, vol. 49, pp. 2897-2904, 2001. |
| [22] | C.d. Zou, Y.l. Gao, B. Yang, Q.j. Zhai, “Size-dependent melting properties of Sn nanoparticles by chemical reduction synthesis,” Transactions of Nonferrous Metals Society of China (English Edition), vol. 20, pp. 248-253, 2010. |

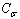 ) and interior (
) and interior (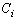 ) average coordination number of metallic clusters, cohesive energy (
) average coordination number of metallic clusters, cohesive energy (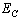 ), and the ratio of atomic bond strength (
), and the ratio of atomic bond strength (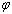 ). It is shown that the proposed model would be able to predict the melting point of embedded NPs (
). It is shown that the proposed model would be able to predict the melting point of embedded NPs (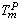 ) as a function of their sizes. The results are compared with experimental data.
) as a function of their sizes. The results are compared with experimental data.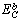 ) could be obtained as:
) could be obtained as: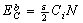
 is the bond strength and
is the bond strength and  is total number of cluster atoms which consists of the interior (
is total number of cluster atoms which consists of the interior ( ) and the surface (
) and the surface (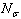 ) atoms.The cohesive energy for a freestanding NP at previous works was obtained as follows[15,16]:
) atoms.The cohesive energy for a freestanding NP at previous works was obtained as follows[15,16]: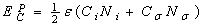
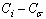 ) make new bonds with the embedding matrix. The energy of this new bond is
) make new bonds with the embedding matrix. The energy of this new bond is 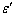 . Therefore cohesive energy of embedded NPs can be expressed by:
. Therefore cohesive energy of embedded NPs can be expressed by: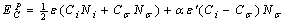
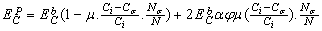
 denotes the ratio of
denotes the ratio of  ,
, 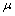 is shape factor[17] and
is shape factor[17] and 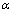 [18] is the correlation number between atoms of the NPs and those of the surrounding matrix. When
[18] is the correlation number between atoms of the NPs and those of the surrounding matrix. When 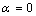 the Eq. (4) could be used for freestanding NPs and
the Eq. (4) could be used for freestanding NPs and 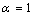 is for coherent interface between embedded NPs and host matrix.After simplifying of Eq. (4), the proportion of the NPs’ cohesive energy to the bulk state can be obtained as:
is for coherent interface between embedded NPs and host matrix.After simplifying of Eq. (4), the proportion of the NPs’ cohesive energy to the bulk state can be obtained as: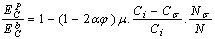
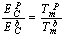
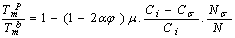
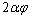 is more than one, NPs exhibit superheating above the melting point of corresponding bulk crystal. But in the inert substrates, the tendency of making bonds between the NPs and the substrate (
is more than one, NPs exhibit superheating above the melting point of corresponding bulk crystal. But in the inert substrates, the tendency of making bonds between the NPs and the substrate (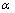 ) decreases. Hence the superheating declines.Surface (
) decreases. Hence the superheating declines.Surface (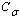 ) and interior (
) and interior (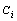 ) average coordination number, Surface (
) average coordination number, Surface (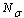 ) and total (
) and total (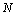 ) atoms of a cluster can be calculated by a manner presented in the authors’ previous works[15,16]. Shape factor for body centered cubic (BCC) and FCC structures have been mentioned in Table 1.
) atoms of a cluster can be calculated by a manner presented in the authors’ previous works[15,16]. Shape factor for body centered cubic (BCC) and FCC structures have been mentioned in Table 1.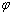 constant have been summarized in Table 2.Figure 1 presents a comparison between the Eq. (7) for
constant have been summarized in Table 2.Figure 1 presents a comparison between the Eq. (7) for 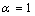 , the models of Nanda et al.[18] and Jiang et al.[5,6], and the experimental results[10] of the superheating behavior of In NPs embedded in Al matrix. In with BCT structure was supposed to be BCC for a simplifying purpose. The liquid-drop model of Nanda et al.[18] overestimates the melting point of embedded In NPs in Al matrix. For NPs having diameter higher than 30 nm the model of Jiang et al.[5,6] has a credible prediction, but for lower than 30 nm our modeling is more eligible. It can be observed that the whole of models predict increasing melting point with decreasing particle size. This fact could be explained by the ratio of surface to interior atoms which increases with decreasing NP size. The bond energy between NP and matrix atoms (
, the models of Nanda et al.[18] and Jiang et al.[5,6], and the experimental results[10] of the superheating behavior of In NPs embedded in Al matrix. In with BCT structure was supposed to be BCC for a simplifying purpose. The liquid-drop model of Nanda et al.[18] overestimates the melting point of embedded In NPs in Al matrix. For NPs having diameter higher than 30 nm the model of Jiang et al.[5,6] has a credible prediction, but for lower than 30 nm our modeling is more eligible. It can be observed that the whole of models predict increasing melting point with decreasing particle size. This fact could be explained by the ratio of surface to interior atoms which increases with decreasing NP size. The bond energy between NP and matrix atoms (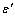 ) is more than the bond energy of NP atoms (
) is more than the bond energy of NP atoms (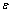 ) in this case, hence the superheating behavior occurs. In other words, suppression of thermal vibration of atoms on the NPs’ interface causes superheating due to coherent interfaces with strong atomic bonds. The Eq. (7) for
) in this case, hence the superheating behavior occurs. In other words, suppression of thermal vibration of atoms on the NPs’ interface causes superheating due to coherent interfaces with strong atomic bonds. The Eq. (7) for 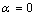 has been compared with experimental results of freestanding In NPs[20], and they show good agreement.
has been compared with experimental results of freestanding In NPs[20], and they show good agreement.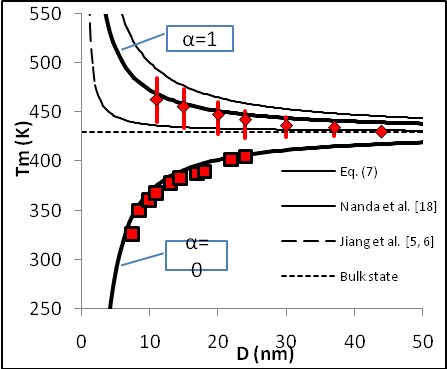
 ) and freestanding (
) and freestanding (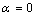 ) In NPs melting point with the size
) In NPs melting point with the size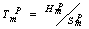 , where
, where 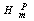 and
and 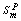 are melting enthalpy and entropy of NP, respectively.
are melting enthalpy and entropy of NP, respectively.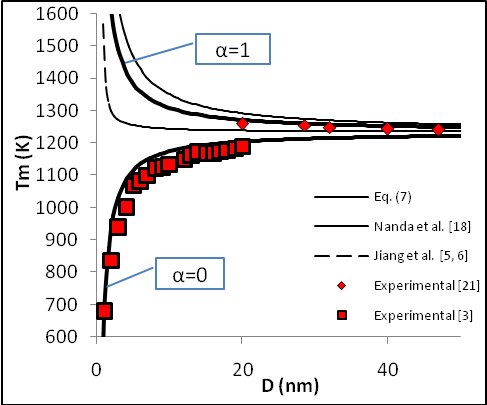
 ) and freestanding (
) and freestanding (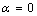 ) Ag NPs melting point with the size
) Ag NPs melting point with the size
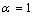 ) and freestanding (
) and freestanding (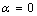 ) Sn NPs melting point with the size
) Sn NPs melting point with the size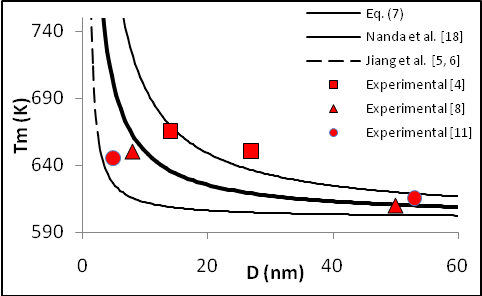
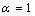 ) Pb NPs melting point with the size
) Pb NPs melting point with the size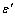 ), which is more than the bond energy between the interior atoms of cluster (
), which is more than the bond energy between the interior atoms of cluster (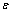 ). For embedded NPs with coherent interface (
). For embedded NPs with coherent interface (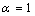 ) and
) and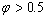 , superheating can be observed. The results show this model is in good agreement with experimental data for superheating of embedded NPs in a matrix.
, superheating can be observed. The results show this model is in good agreement with experimental data for superheating of embedded NPs in a matrix. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML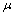
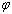 constant
constant