| [1] | Samson Mil’shtein, P. Ersland, “Progress of quantum electronics and the future of wireless technologies,” Microelectronics Journal, vol. 39, issues 3-4, March–April 2008, pp. 669-673. |
| [2] | S. Mil’shtein, C. Liessner, “High Speed switch using pairs of pHEMTs with shifted gates,” Microelectronics Journal, vol. 36, issues 3-6, March-June 2005, pp. 316-318. |
| [3] | Christopher W. Liessner. 2005. “A high speed RF switch using shifted-gate pHEMTs,” University of Massachusetts, Lowell. |
| [4] | Michael Roberts, Lutfi Albasha, Wolfgang Bosch, Damian Gotch, James Mayock, Pallavi Sandhiya, Ian Bisby, “Highly Linear Low Voltage GaAs pHEMT MMIC Switches for Multimode Wireless Handset Applications,” IEEE Radio and Wireless Conference, August 19-22, 2001, pp. 61-64. |
| [5] | Zeji Gu, Dave Johnson, Steven Belletete, Dave Fryklund, “Low Insertion Loss and High Linearity PHEMT SPDT and SP3T Switch ICs for WLAN 802.11a/b/g Applications,” IEEE Radio Frequency Integrated Circuits (RFIC) Symposium, Digest of Paper, June 6-8, 2004, pp. 505-508. |
| [6] | J. A. del Alamo, “The High Electron Mobility Transistor at 30: Impressive Accomplishments and Exciting Prospects,” International Conference on Compound Semiconductor Manufacturing Technology, May 16-19, 2011, pp. 17-22. |
| [7] | Jay Yang, Rick Cory, “Ultra-Miniature High Linearity SPDT Switch for WLAN Applications,” Microwave Product Digest, February 2010. |
| [8] | Kevin Walsh, “RF Switches Guide Signals in Smart Phones,” Microwaves & RF, September 2010, vol. 49, issue 9, p. 80. |
| [9] | Chang-Ho Lee, Bhaskar Banerjee, Joy Laskar, “Novel T/R Switch Architectures for MIMO Applications,” IEEE MTT-S International Microwave Symposium Digest, vol. 2, pp. 1137-1140. |
| [10] | Robert H. Caverly, “Distortion in Broad-Band Gallium Arsenide MESFET Control and Switch Circuits,” IEEE Transactions on Microwave Theory and Techniques, vol. 39, no. 4, pp. 713-717, 1991. |
| [11] | Kai Chang, Inder Bahl, Vishay Nair. 2002. “RF and Microwave Circuit and Component Design for Wireless Systems” Wiley, John & Sons, Incorporated, New York, p. 222. |
| [12] | C. –J. Wei, A. Klimashov, Y. Zhu, E. Lawrence, G. Tkachenko, “Large-Signal PHEMT Switch Model, Which Accurately Predicts Harmonics and Two-Tone Inter-Modulation Distortion,” IEEE MTT-S International Microwave Symposium Digest, June 12-17,2005. |
| [13] | Yu Zhu, Cejun Wei, George Nohra, Cindy Zhang, Oleksiv Klimashov, Hong Yin, Dylan Bartle, “Electromagnetic Only HEMT Model for Switch Design,” Asia Pacific Microwave Conference, December 7-10, 2009 , pp. 273-276. |
| [14] | Dong-Ming Lin, Chien-Chang Huang, Yi-Jen Chan, “A Symmetrical Model for Microwave Power AlGaAs/InGaAs pHEMTs for Switch Circuit Applications,” IEEE Transactions on Electron Devices, vol. 56, no. 11, pp. 2638-2643, 2009. |
| [15] | Ce-Jun Wei, Yu Zhu, Hong Yin, Olesky Klimashov, Dylan Bartle, “A Comprehensive PHEMT Core Model for Switch Applications,” IEEE MTT-S International Microwave Symposium Digest, June 5-10, 2011, pp. 1-4. |
| [16] | Ce-Jun Wei, Hong Yin, Olesky Klimashov, Yu Zhu, Dylan Bartle, “Multi-gate pHEMT Modeling for Switch Applications,” IEEE Compound Semiconductor Integrated Circuit Symposium, October 14-17, 2012, pp. 1-4. |
| [17] | Faramarz Kharabi, “Modeling of FET Switches,” IEEE Compound Semiconductor Integrated Circuit Symposium, October 14-17, 2012, pp. 1-4. |
| [18] | Ce-Jun Wei, Yu Zhu, Alex Klimashov, Hong Yin, Cindy Zhang, Dylan Bartle, “Distributed Switch FET Model that Predicts Better Insertion Loss and Harmonics,” European Microwave Integrated Circuits Conference, pp.238-241. |
| [19] | P. J. Rudge, R. E. Miles, M. B. Steer, and C. M. Snowden, “Investigation into Intermodulation Distortion in HEMTs Using a Quasi-2-D Physical Model,” IEEE Transactions on Microwave Theory and Techniques, vol. 49, no. 12, pp. 2315-2321, 2001. |
| [20] | P. R. Pantoja, M. J. Howes, J. R. Richardson, and C. M. Snowden, “A Large-Signal Physical MESFET Model for Computer-Aided Design and Its Applications,” IEEE Transactions on Microwave Theory and Techniques, vol. 37, no. 12, pp. 2039-2045, 1989. |
| [21] | R. J. Trew, “MESFET Models for Microwave Computer-Aided Design,” Microwave Journal, vol. 33, pp 115-130, May 1990. |
| [22] | R.B. Hallgren and P. H. Litzenberg, “TOM3 Capacitance Model: Linking Large- and Small-Signal MESFET Models in SPICE,” IEEE Transactions on Microwave Theory and Techniques, vol. 47, no. 5, pp. 556-561, 1999. |
| [23] | W. R. Curtice, “A MESFET Model for Use in the Design of GaAs Integrated Circuits,” IEEE Transactions on Microwave Theory and Techniques, vol. 28, no 5, pp. 448-456, 1980. |
| [24] | L. Angelov, N. Roreman, J. Stenarson, M. Garcia, and H. Zirath, “An Empirical Table-Based FET Model,” IEEE Transactions on Microwave Theory and Techniques, vol. 47, no. 12, pp. 2350-2357, 1999. |
| [25] | J. Gao, X. Li, H. Wang, and G. Boeck, “Empirical All region Current Based PHEMT DC Model,” SBMO/IEEE MTT-S International Microwave and Optoelectronics Conference, 2003. Proceedings of the 2003, vol. 1, no. 9, pp. 99-101. |
| [26] | G. Qu, A. E. Parker, “Modeling HEMT intermodulation distortion characteristics,” Microelectronics Journal, vol. 31, issue 7, July 2000, pp. 493-496. |
| [27] | Ristesh Gupta, Sandeep Kumar Aggarwal, Mridula Gupta, R. S. Gupta, “Analytical non-linear charge control model for InAlAs/InGaAs/InAlAs double heterostructure high electron mobility transistor (DH-HEMT),” Solid-State Electronics, vol. 49, issue 2, February 2005, pp. 167-174. |
| [28] | Michael Wren, Thomas J. Brazil, “Enhanced Prediction of pHEMT Nonlinear Distortion Using a Novel Charge Conservative Model,” IEEE MTT-S International Microwave Symposium Digest, vol. 1, pp. 31-34, June 6-11, 2004. |
| [29] | Paul M. White, Wolfram C. Stiebler, Philip C. Balas, “Improved Modified Materka Model for Simulation of Pinch-Off Variation in PHEMT Devices,” European Microwave Integrated Circuits Conference, pp. 414-416, September 10-13, 2006. |
| [30] | Ritesh Gupta, Sandeep k. Aggarwhal, Mridula Gupta, R. S. Gupta, “An analytical model for discretized doped InAlAs/InGaAs heterojunction HEMT for higher cut-off frequency and reliability,” Microelectronics Journal, vol. 37, issue 9, September 2006, pp. 919-929. |
| [31] | B. Luo, Y. X. Guo, S. Y. Wong, L. C. Ong, “Modeling of 0.15μm InGaAs pHEMT up to 60 GHz,” IEEE International Workshop on Radio-Frequency Integration Technology, 2007, December 9-11, 2007, pp. 286-289. |
| [32] | Ce-Jun Wei, Yu Zhu, Hong Yin, Oleksiy Klimashov, Cindy Zhang, Tzung-Yin Lee, “Capacitance and RF-Conductance/ Transconductance Look-up Table Based pHEMT Model,” Asia-Pacific Microwave Conference Proceedings, December 5-8, 2011, pp. 1246-1249. |
| [33] | A. Raffo, A Santtarelli, P.A. Traverso, M. Pagani, F. Palomba, F. Scappaviva, G. Vannini, F. Filicori, “Improvement of PHEMT Intermodulation Prediction Through the Accurate Modelling of Low-Frequency Dispersion Effects,” IEEE MTT-S International Microwave Symposium Digest, June 12-17, 2005. |
| [34] | Masaya Iwamoto, Jianjun Xu, Jason Horn, David E. Root, “III-V FET High Frequency Model with Drift and Depletion Charges,” IEEE MTT-S International Microwave Symposium Digest, June 5-10, 2011, pp. 1-4. |
| [35] | Zeji Gu, Shuyun Zhang, David Johnson, Steve Belletete, Mark Ayvazian, Dave Fryklund, “A High-Performance GaAs SP3T Switch for Digital Cellular Systems,” IEEE MTT-S International Microwave Symposium Digest, May 20-24, 2001, vo. 1, pp. 241-244. |
| [36] | Yen-Wei Chen, Wei-Chou Hsu, Rong-Tay Hsu, Yue-Huei Wu, Yeong-Jia Chen, “Characteristics of In0.52Al0.48As/ InxGa1-xAs HEMT’s with various InxGa1-xAs channels,” Solid-State Electronics, vol. 48, issue 1, January 2004, pp. 119-124. |
| [37] | A. M. Street, “RF Switch Design,” How to Design RF Circuits (Ref. No. 2000/027), IEEE Training Course, 2000, pp. 4/1-4/7. |
| [38] | Yueh-Chin Lin, J. W. Chang, Edward Yi Chang, X. Y. Chang, “On the Doping Effects for Linearity Improvement of InGaP/InGaAs PHEMT,” Asia-Pacific Microwave Conference Proceedings, vol. 2, December 4-7, 2005. |
| [39] | S. Mil’shtein and C. Liessner “Field Effect Transistor with Shifted Gate” Patent# 11,407,381 (2006) |
| [40] | S. Mil’shtein, J.Palma, and C. Liessner “Field Effect Transistor with Independently Biased Gates” Patent # 11,406,838 (2006) |
| [41] | C. Liessner, J. Barrett, J. Palma, D. Gleason, and S. Mil’shtein, “Improving FET Switch Linearity”, Electron Devices, Vol. 54, Number 3, March 2007, pp. 391-397. |
| [42] | H. C. Chiu, C. W. Chen, Y. C. Huang, R. J. Yang, “RF Performance of Double Heterojunction High Mobility Transistor with Various Lower/Upper Plana Doping Ratio Designs on SPST Switchs Application,” Asia-Pacific Microwave Conference, December 11-14, 2007, pp. 1-4. |
| [43] | Y. S. Lin, S. K. Liang, “Improved AlGaAs/InGaAs High-Electron Mobility Transistor,” IEEE Transactions on Microwave Theory and Techniques, vol. 41, issue 5, pp. 752-759, 1993. |
| [44] | Andrew Freeston, Costas Varmazis, Timothy Boles, “Nanosecond pHEMT Switches,” European Microwave Integrated Circuits Conference, September 28-29, 2009, pp. 13-16. |
| [45] | Robert H. Caverly, “Distortion in Off-State Arsenide MESFET Switches,” IEEE Transactions on Microwave Theory and Techniques, vol. 41, no. 8, pp. 1323-1328, 1993. |
| [46] | Andrew Dearn, Liam Devlin, Wing Yau, Owen Yu, “Design Trade-offs for High Linearity pHEMT Switches,” 53rd IEEE International Midwest Symposium on Circuits and Systems, August 1-4, 2010, pp. 942-945. |
| [47] | Shigeki Koya, Takashi Ogawa, Hiroyuki Takazawa, Akishige Nakajima, Shinya Osakabe, Yasushi Shigeno, Shinichiro Takatani, “Intergate-Channel-Connected Multi-Gate PHEMT Devices for Antenna Switch Applications,” IEEE MTT-S International Microwave Symposium Digest, June 15-20, 2008, pp. 1287-1290. |
| [48] | S. Mil’shtein, P. Ersland, S. Somisetty, C. Gil, “p-HEMT with tailored field,” Microelectronics Journal, vol. 34, no.5, May 2003, pp. 359-361. |
| [49] | S. Mil’Shtein, “Shaping electrical field in heterostructure transistors,” Microelectronics Journal, vol. 36, issues 3-6, March-June 2005, pp. 319-322. |
| [50] | Walter A. Wohlmuth, Wolfgang Liebl, Varun Juneja, Robert Hallgren, Wayne Struble, Domingo Faria, Paul Litzenberg, Otto Berger, “E-/D-pHEMT Technology for Wireless Components,” IEEE CSIC Symposium, 2004, pp. 115-118. |
| [51] | Sobhana V. Gudimetta. 2003. “Control of HEMT performance by changing the quantization conditions for electrons,” University of Massachusetts, Lowell. |

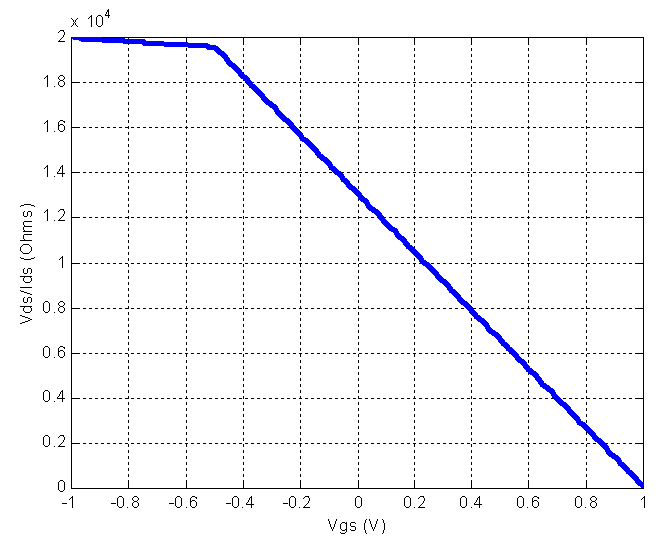
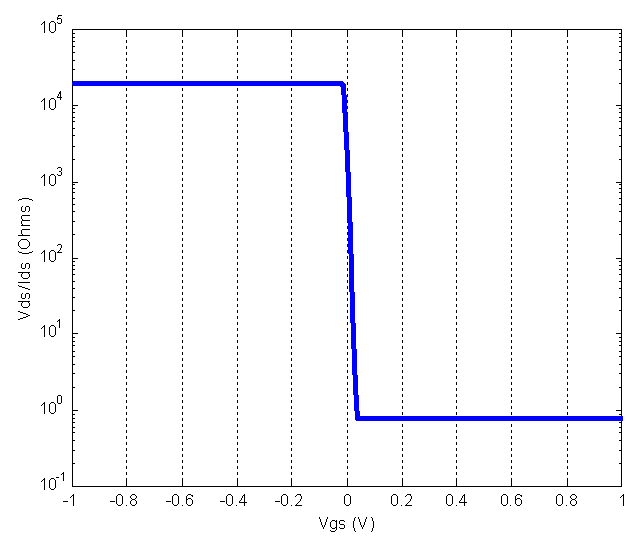
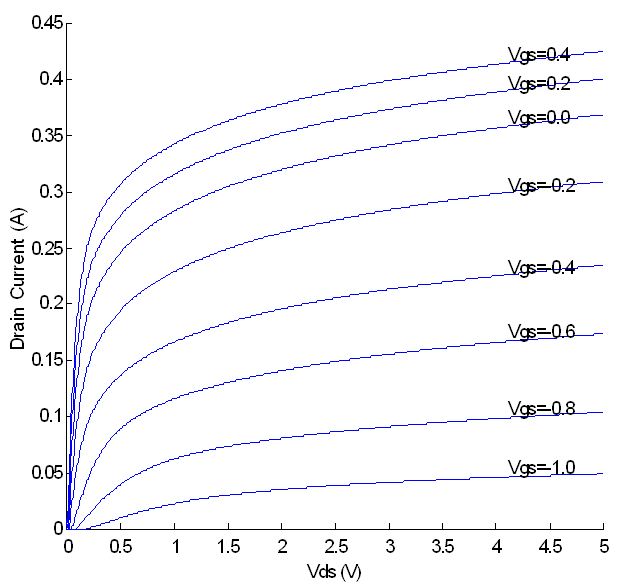
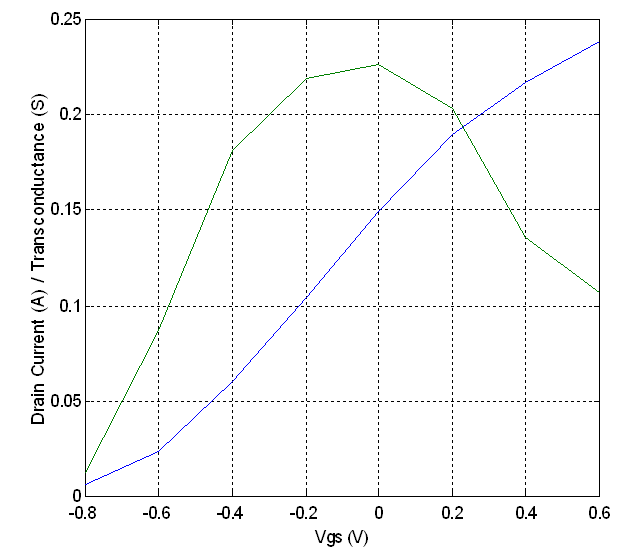
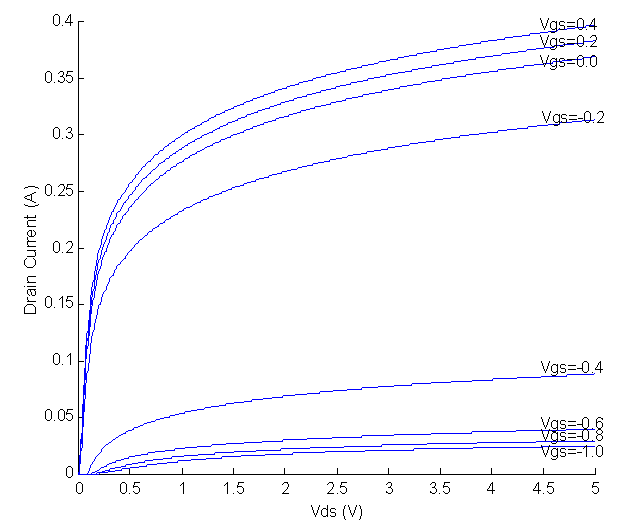
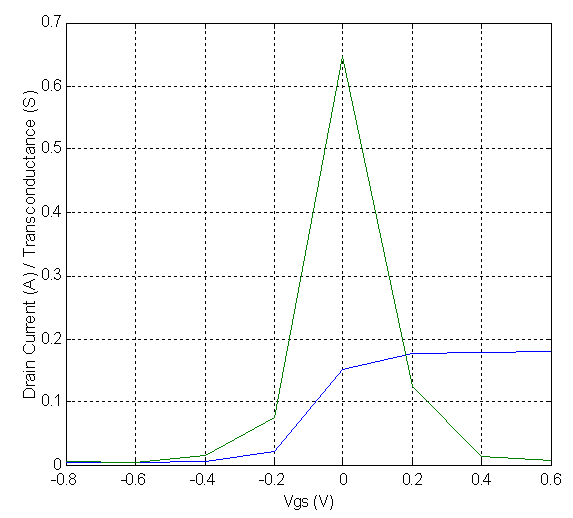
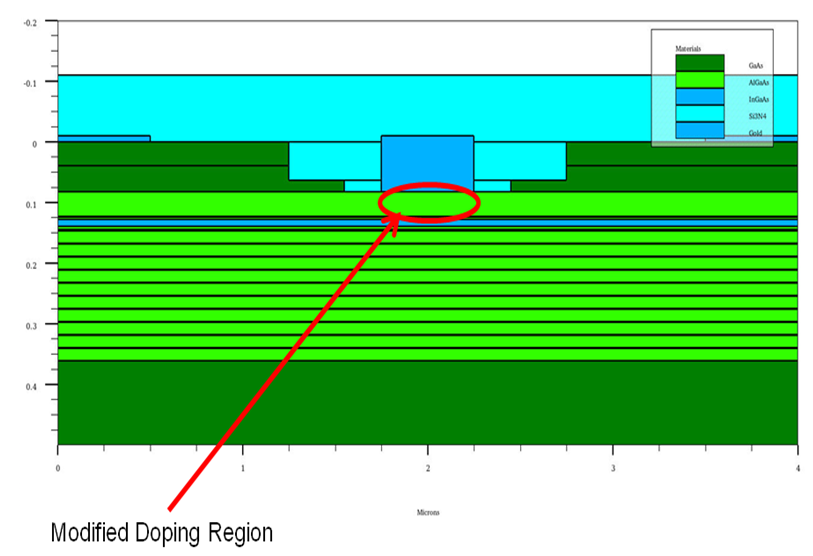
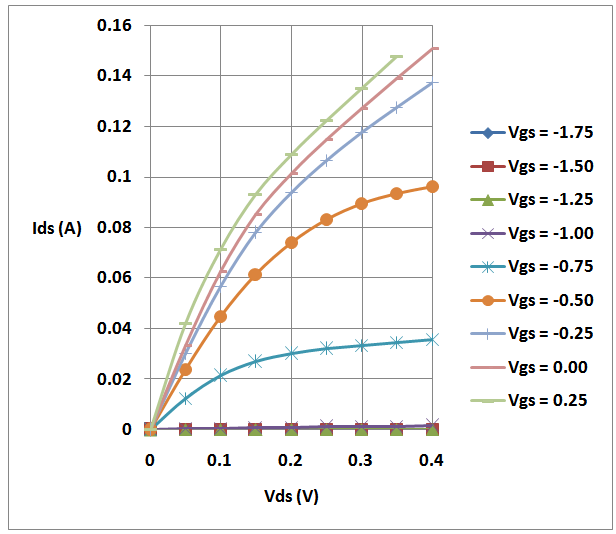
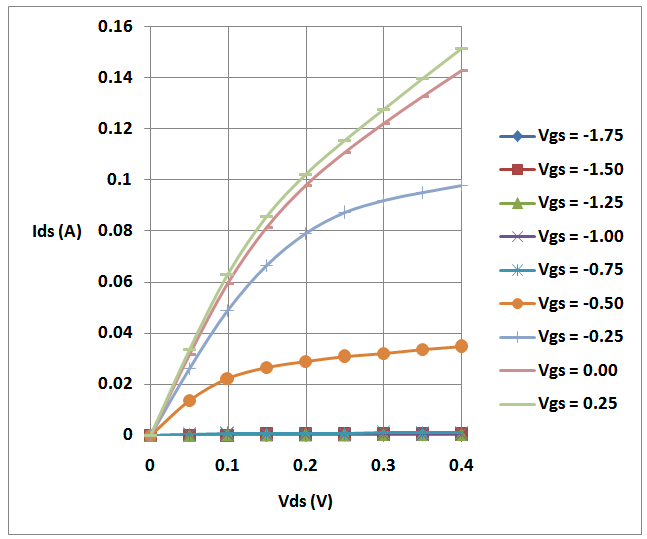
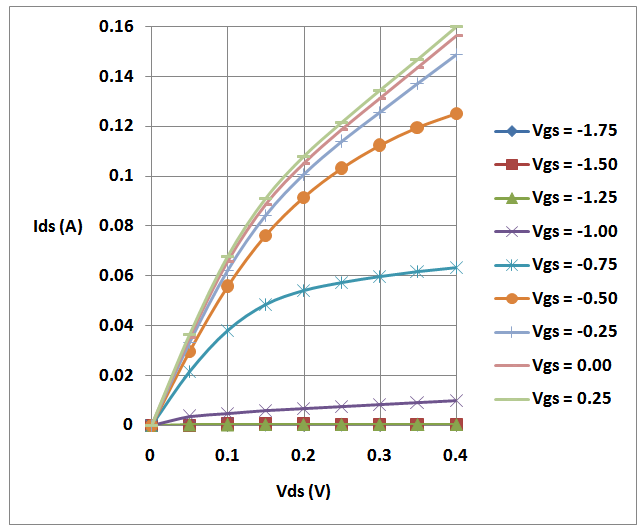
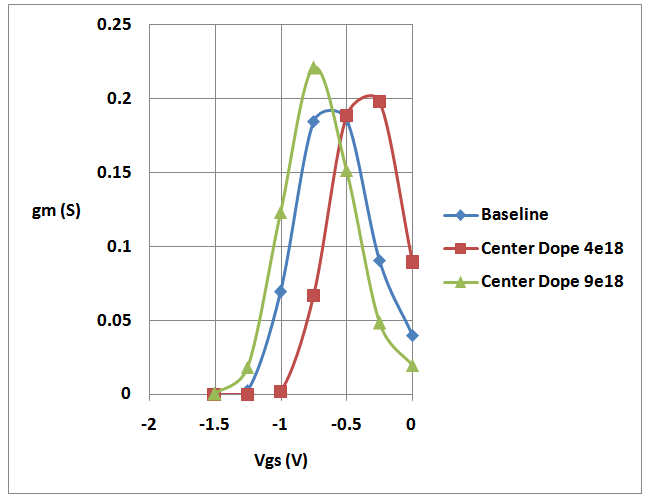
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML