Sergio Manzetti
Fjordforsk Environmental Health and Technology, 5743, Flåm. Norway
Correspondence to: Sergio Manzetti , Fjordforsk Environmental Health and Technology, 5743, Flåm. Norway.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Hurricanes, cyclones and typhoons are weather phenomena which induce damages for billions of dollars yearly and pose significant risks to communities worldwide. The need for better meteorological prediction methods is therefore more important than ever, particularly with the emergence of “extreme weather” conditions. Super-computer methods are key tools for storm-analysis and prediction, and are used frequently to predict the direction of large low-pressure systems such as Hurricanes heading yearly for American continent, cyclones in Australia and typhoons in Japan. The dynamical behaviour of these vast low-pressure systems is not fully understood, and the directions of these weather phenomena are often resolved too late for evacuation procedures to be fully effective. In order to increase the understanding of low-pressure systems and meteorological prediction, a hybrid view on the behaviour of hurricane systems based on a blend of quantum mechanics and classical physics is introduced in this brief note. The aims are to introduce a mathematical contemplation to bring to the attention of meteorological modelers a putative behaviour of the storm systems analogue with electron orbital density functional theory, and to use electron orbital theory to improve the resolution and predictive power of storm modeling. The mathematical discussion presented herein shows that a low-pressure system can be subdivided into N-layers, with physical and energetical qualities. Such qualities comprise angular momenta and individual energies of high-density regions which can be used to predict the direction of the low-pressure system. The results and mathematical discussion presented herein serve as a foundation for Hurricane theory improvement.
Keywords:
Prediction, Atmospheric Systems, Low Pressure, Modeling, Density Functional, Electron Orbital, Mathematics, Computational Sciences
1. Introduction
Modern weather prediction has evolved since the beginning 1950s, when the first computational clusters were assembled for parallel synchronized computing 1.High- performance computing has aided in predicting the behaviour of large low-pressure systems, such as hurricanes and tropical storms, electronic structure calculations, molecular dynamic studies and also pollution dynamics in tropospheric environments 2-5. Simultaneously, the need to understand better the behaviour of hurricanes has escalated in the last 20 years, particularly with the emergence of extreme weather conditions 6. The case of extreme weather is inducing changes in storm activities on the northern and southern hemispheres in particular 7, which often defy regular storm behaviour and bring unusually strong weather changes over short periods oftime.For instance, the emergence of storms in the Atlantic Ocean which lead to the yearly hurricanes on the Mexican gulf and east coast of US is an example of weather systems that are affected by global warming. Some pitfalls related with the Atlantic storms are their directional mode which is particularly difficult to estimate. The orientation of the storms directed toward the US inclines for instance in mainly four directions, 1) to the Northern part of the East Coast – towards Louisiana, New York, or 2) the Florida Keys and Bermuda (such as Hurricane Andrew7), 3) towards the Northern part of the Mexican Gulf (including New Orleans – such as Hurricane Katrina 8) or 4) towards the Central American portion of the American Continent (such as Hurricane Mitch) 9.Given the complexity of such weather systems, the predictive methodology is unilaterally dependent on numerical methods. The advantage of numerical methods is their empirical nature, based on accurate observations made with sensitive equipment 10-13. However, numerical methods are dependent on considerable risk-taking and dangerous excursions and continuous and expensive sample taking. With these factors involved and continuous change of weather types, an ultimate theory between low-pressure systems, macroelectrostatics and storm-behaviour is required. This paper investigates the use of quantum theory for the prediction of storm behaviour associated with the rotational behaviour of low-pressure systems, such as Hurricanes. The presentation of an N-layer model of low-pressure systems with exchange effects between the N-layers of the storm system is introduced. Macroelectrostatic effects between layers are also briefly discussed.
2. Objectives
The need to find alternative methods for predicting hurricane dynamics is eminent, and may require “out-of-the-box” approaches for a complete elucidation of the dynamics of weather systems, their interaction with oceans and with land masses. Although few approaches have been previously made regarding low-pressure systems as near mechanical entities, the majority of the interpretations of hurricane systems rely on data-collection and numerical solving (vide supra). The objectives of this paper are therefore to introduce a view of weather systems based on a cross-disciplinary context, with microcosmic andmesocos-mic points of considerations. The collections of equations below show this in a comprehensive and sophisticated manner, for the reader to further develop inclinations for understanding better the complexity of weather systems.
3. Methods
The methods for solving the interpretation of hurricane systems by the use of orbital theory will evolve from the combinatory use of classical physics and quantum physics. The use of the uncertainty principle is herein included in the quantum physics part, which acclaims the consideration of the weather system as a system composed of particles. The composition of individual components in the system is then correlated by electrostatic interactions, of simple electrophysical nature. The further elaboration of the interpretation approaches then the energy of the particle, thus as a mesocosmic entity, with its physical qualities, mass, density, angular velocity and distance to the center of the system. The temperature of the system is an implicit value of the energetic components, which modulates the physical qualities of the rotating entity (described as a mesocosmic particle).
4. Results and Discussion
Low-pressure system representation: N-layer modelThe hurricane can be subdivided into N-layers (Fig 1) each layer is represented by a cylinder with thickness x, a height z and rotating at an angular velocity of ω (the height shall be neglected throughout the paper for simplicity, and the N-layers are represented as 2D-slices). The smaller x becomes, the more accurate the level of interaction between layers can be estimated. The hurricane is moving at a speed v, and extracting one of its layers for analysis as a cylinder, the cylinder is affected by a frictional force, f during its rotation.
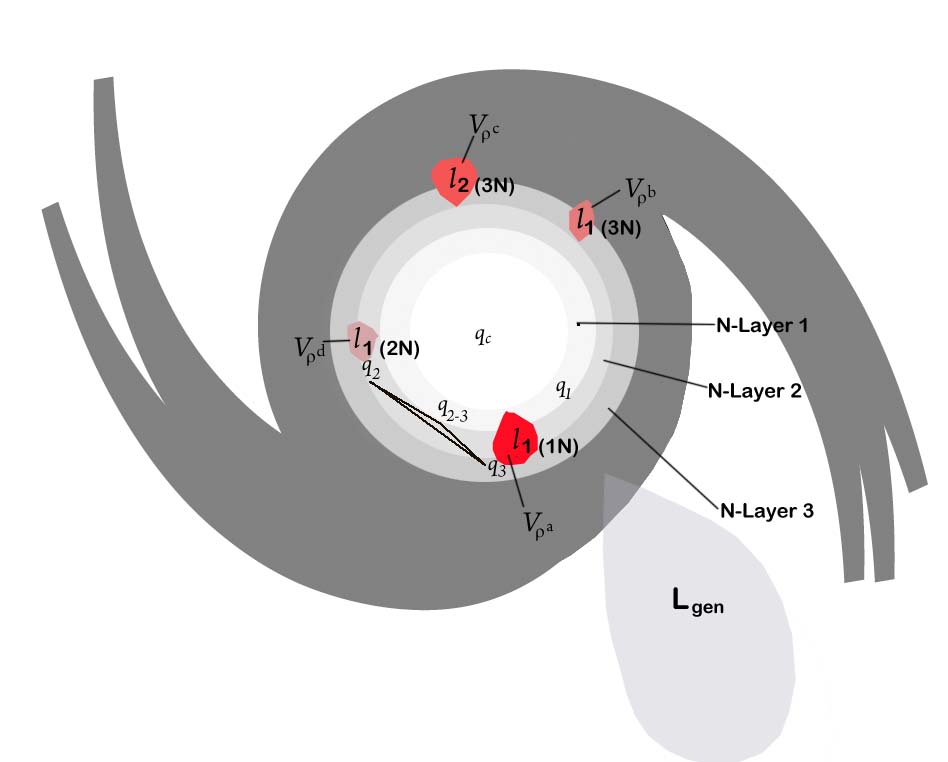 | Figure 1. The relationship between hurricane shape and N-layer subdivision in a 2D slice. The representation of N-layers (1N: layer 1, 2N: layer 2…) aims to facilitate the reductive representation of the hurricane system with its respective values: q: charges; Vρ: volumes of high-density regions, l: angular momenta: L: generalized angular momentum |
Ma = fwhere M is the mass of the layer and a its acceleration (cylinder with given thickness x).Because friction from other layers can accelerate or decelerate the translational motion of the layer, the layers’ rotational equation takes the form:I ω = -f rWhere I is the moment of inertia and r is the radius of layer to the center of the hurricane. If the layer is “slipping” along its rotational path because of the rotational effect by other layers, then the friction force f is equal to the coefficient of friction, µ multiplied by the normal reaction force at the surface M s :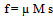 | (1) |
where M is the mass of the cylinder, and s is the centripetal acceleration induced by the entire multilayered low-pressure system on the layer.Regional N-layer density as a point with specific angular momentum.The rotating entity of the low-pressure hurricane contains N-layers (Fig 1), each defined by the classical rules described above. The energetic description of each layer is thus defined by its regional moist density. For simplicity, a model can consider only the volume within the N-layer of highest-moist density, Vρ as reference of N-layer. The volume is defined within a threshold moist-density region, ρtr, which is subjected to an air pressure, π.The energy of the “particle” (high moist-density volume) is described as the energy of any rotating particle around a center (storm centre). The kinetic energy of the “particle” is thus: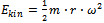 | (2) |
where m is the mass of the high density area, r is the distance of the center of the high density area to the storm center, and ω, its angular velocity.The high-density volume defined within the N-layer has a potential energy (Epot) respective to the storm center. This potential energy is discussed in the next paragraph accordingly with the macroelectrostatic attraction between moist ensembles governed by the dielectric constant of water (in moist), the electrostatic attraction between charges and the total electrical charge of the periphery of the low-pressure system and the centre. This energy exerted by the center on the N-layers is defined as Epot. The energy of the regional densityThe energy of the high density region is thus: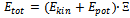 | (3) |
And Ξ is the differential equation of the energy function (χ) over spatial coordinates: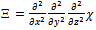 | (4) |
Equation (4) describes the dynamical behaviour of the high-density region of the low-pressure system as affected by the energy function χ: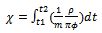 | (5) |
Equation (5) represents the change over time of the proportional relationship between moist density (ρ), for the high-density region, its mass m, and its air-pressure (π), multiplied by the angle of rotation (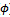 ) of the measured high-moist density region around the storm centre. The ultimate value of the function results in mass/energy unit, which represents the level of mass required to promote an amount of energy, within the high-density region with the N-layer. This very relationship is measured and integrated over time to give a relationship between the change of energy and mass in the high-density region within the N-layer. In a figurative sense, this high-density region appears as a “large-scale electron” compared to the nucleus of the storm, its center. Equation (3) is familiar to the spatial representation of the free particle movement in quantum chemistry, which is of non-undular quality and which is not apparently governed by the uncertainty principle 14 as applied to solve the energy of the system by the Schrödinger equation 15. Ξ brings the focus on the relationship between mass, force and rotational dynamics, where the ρ/π
) of the measured high-moist density region around the storm centre. The ultimate value of the function results in mass/energy unit, which represents the level of mass required to promote an amount of energy, within the high-density region with the N-layer. This very relationship is measured and integrated over time to give a relationship between the change of energy and mass in the high-density region within the N-layer. In a figurative sense, this high-density region appears as a “large-scale electron” compared to the nucleus of the storm, its center. Equation (3) is familiar to the spatial representation of the free particle movement in quantum chemistry, which is of non-undular quality and which is not apparently governed by the uncertainty principle 14 as applied to solve the energy of the system by the Schrödinger equation 15. Ξ brings the focus on the relationship between mass, force and rotational dynamics, where the ρ/π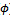 unit gives a mass/energy relationship. Because the air-pressure is ultimately affected by sea and air temperature, Ξ includes these terms as well, based on measurements.The less trivial aspect is that the relationship between air pressure and moist density is not harmonic and relies on measurements to be determined in order to conclude an approximate function, χ. The approximated function can be deduced by a series of hurricane measurement from past recordings and serve to deduce approximated functions. The function χ is thus used to add a variable to the energetic view of the storm layers as a pattern of non-harmonic behaviour, where it includes air-pressure and moist-density and assigns a principal qualitative aspect to the contemplation of the energy of the N-layer of the low-pressure system, Ξ.Because the N-layer high-density volume is continuously changing in position and density, its generalized angular momentum (as a mean value of a series of angular momenta) is used as reference for its physical quality, analogously to the angular momentum of the free particle description of the electron 16. The angular momentum of the regional density is defined by:
unit gives a mass/energy relationship. Because the air-pressure is ultimately affected by sea and air temperature, Ξ includes these terms as well, based on measurements.The less trivial aspect is that the relationship between air pressure and moist density is not harmonic and relies on measurements to be determined in order to conclude an approximate function, χ. The approximated function can be deduced by a series of hurricane measurement from past recordings and serve to deduce approximated functions. The function χ is thus used to add a variable to the energetic view of the storm layers as a pattern of non-harmonic behaviour, where it includes air-pressure and moist-density and assigns a principal qualitative aspect to the contemplation of the energy of the N-layer of the low-pressure system, Ξ.Because the N-layer high-density volume is continuously changing in position and density, its generalized angular momentum (as a mean value of a series of angular momenta) is used as reference for its physical quality, analogously to the angular momentum of the free particle description of the electron 16. The angular momentum of the regional density is defined by: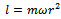 | (6) |
where m is the mass of the high density area, r is the distance of the center of the high density area to the storm center, and ω its angular velocity.The generalized angular momentum of the regional density is deduced as a mean valued angular momentum approximated by a series of measured and estimated angular momenta. The generalized angular momentum is thus described as the overall angular momentum of the N-layer.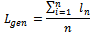 Potential EnergyThe total potential energy of the N-layer to the centre of the hurricane can be deduced by accounting for the following factors:1) Relative permittivity of the storm medium (moist).2) The electrostatic interaction between N-layers.3) The electrostatic interaction between each N-layer and the storm center (Epot) in accord with their macro-electrical charge.4) A form for the potential energy approximated by the similar expression of the potential energy of an atomic system in the form:
Potential EnergyThe total potential energy of the N-layer to the centre of the hurricane can be deduced by accounting for the following factors:1) Relative permittivity of the storm medium (moist).2) The electrostatic interaction between N-layers.3) The electrostatic interaction between each N-layer and the storm center (Epot) in accord with their macro-electrical charge.4) A form for the potential energy approximated by the similar expression of the potential energy of an atomic system in the form: 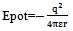 1) Relative permittivity:
1) Relative permittivity: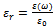 | (7) |
is calculated to εr=22.0 17. Variations of levels of humidity degree to permittivity are to be accounted for, in order to relate εr with moist density (ρ).2) Electrostatic interaction between N-layers:Each charge of an N-layer, q, is governed by the charge of the macro-electric field it exists in, as defined by Coulombs Law: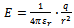 | (8) |
where q is the charge of the system, r is the distance from the N-layer to the center of the storm and εr is the relative permittivity in moist medium.Each of the N-layers are assigned a charge, which can be localized to their high-density regions used as reference points. The interaction of the reference points may simplify the overall estimation of charge interactions, where the charge of reference point 1, q1 and reference point 2, q2, can be summarized to a “mid-point charge” located midpoint between the two high-density regions of the two respective N-layers, in accord with the Coulomb potential. The potential energy of the midpoint is given in accord with the Coulomb potential (8).3) Electrostatic interaction between N-layer and storm center.As a contemplation of the storm system as an atomic system, the distance from the centre to the N-layer modulates its potential energy. The factors described in (1) account for the mechanical energy of the N-layer, however theelectro- static attraction/repulsion between the N-layer and the centre will have to be solved based on the notion: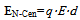 | (9) |
Where q is the charge of the N-layer, d is the distance from the N-layer to the storm centre and E is the electric field intensity: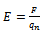 | (10) |
Where F is the electric force experienced by the N-layer, and qn is the charge of the N-layer.4) Potential energy formed from particle-physics laws.As the potential energy of an atomic system is given by: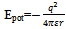 The equivalent relation for a macroscopic environment would be:
The equivalent relation for a macroscopic environment would be: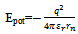 where εr is the moist permittivity constant and rn is the distance from the N-layer to the storm centre.
where εr is the moist permittivity constant and rn is the distance from the N-layer to the storm centre.
5. Conclusions
The combination of classical physics and quantum physics is a challenge when comparing macroscopic environments and sub-atomic systems. The inclusion of high-density volume regions as pivotal for describing the behaviour of storm layers (N-layers) is an approach to solve the complex energetical fluxes of the storm, which thereby govern the orientation and path of movement of the low-pressure system. The approach to relate kinetic and potential energy into a total energy relies on a proper representation of a potential energy of a layer in relation to the storm centre. This approach aims to include macroelectrostatics and ma- croenergetics, which depend on several discussed factors. These factors include non-trivially solved equations where the total energy of the system is represented and can serve as the foundation for the prediction of behaviour and direction of the hurricane system. For this reason, the author submits this initial note to stimulate for collaboration and interaction amongst the atmospheric scientific community in order to instigate novel methods of weather interpretation.
References
| [1] | Kilburn T. (1949). The University of Manchester universal high-speed digital computing machine. Nature. 164:684-7. |
| [2] | Malmerberg E, Omran Z, Hub JS, Li X, Katona G, Westenhoff S, Johansson LC, Andersson M, Cammarata M, Wulff M, van der Spoel D, Davidsson J, Specht A, Neutze R. (2001) Time-resolved WAXS reveals acceleratedconformational changes in iodoretinal-substituted proteorhodopsin. Biophys J. 101:1345-53. |
| [3] | Wang Z, van Tol J, Taguchi T, Daniels MR, Christou G, Dalal NS. (2011). Mn(7) Species with an S = (29)/(2) Ground State: High-Frequency EPR Studies of a Species at the Classical/Quantum Spin Interface. J Am Chem Soc. 133:17586-9. |
| [4] | Sathye A, Xue M, Bassett G, Droegemeier K. (1997). Parallel weather modeling with the advanced regional prediction system. Parallel Computing, 23:2243-2256 |
| [5] | Carnevale C, Decanini E, Volta M. (2008). Design and validation of a multiphase 3D model to simulate tropospheric pollution. Science of The Total Environment, 390:166-176 |
| [6] | Kerr RA. (2011). Climate change. Humans are driving extreme weather; time to prepare. Science. 334:1040. |
| [7] | Zahn M, von Storch H. (2010) Decreased frequency of North Atlantic polar lows associated with future climate warming. Nature. 467:309-12. |
| [8] | Smith SK, McCarty C. (1996). Demographic effects of natural disasters: a case study of Hurricane Andrew. Demography. 33:265-75. |
| [9] | Gramling C. (2005). Hurricane Katrina. Riding out the storm. Science. 20309:1657. |
| [10] | Editor. (1998) Impact of Hurricane Mitch on Central America. Epidemiol Bull. 19:1-13. |
| [11] | Verboom, G.K., Ronde, J.G., Van Dijk, R.P. (1992). A fine grid tidal flow and storm surge model of the North Sea. Continental Shelf Research 12, 213e233. |
| [12] | Hubbert, G.D., McInnes, K.L. (1999). A storm surge inundation model for coastal planning and impact studies. Journal of Coastal Research 15, 168e185. |
| [13] | Xie, L., Pietrafesa, L.J., Peng, M. (2004). Incorporation of a mass-conserving inundation scheme into a three-dimensional storm surge model. Journal of Coastal Research 20, 1209e1223. |
| [14] | Heisenberg, W. (1930), Physikalische Prinzipien der Quantentheorie, Leipzig: Hirzel English translation The Physical Principles of Quantum Theory. Chicago: University of Chicago Press, 1930. |
| [15] | Schrödinger, E. (1926). An Undulatory Theory of the Mechanics of Atoms and Molecule. Physical Review 28 (6): 1049–1070 |
| [16] | Atkins P and Friedman F. (2011). Molecular Quantum Mechanics. Oxford University Press. 5th Edition. New York. |
| [17] | Frank H. (2003). Influence of humidity on the permittivity and conductivity of thin zirconium alloy oxide films. Journal of Nuclear Materials, 321:115-117 |

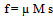
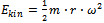
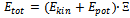
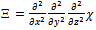
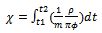
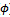 ) of the measured high-moist density region around the storm centre. The ultimate value of the function results in mass/energy unit, which represents the level of mass required to promote an amount of energy, within the high-density region with the N-layer. This very relationship is measured and integrated over time to give a relationship between the change of energy and mass in the high-density region within the N-layer. In a figurative sense, this high-density region appears as a “large-scale electron” compared to the nucleus of the storm, its center. Equation (3) is familiar to the spatial representation of the free particle movement in quantum chemistry, which is of non-undular quality and which is not apparently governed by the uncertainty principle 14 as applied to solve the energy of the system by the Schrödinger equation 15. Ξ brings the focus on the relationship between mass, force and rotational dynamics, where the ρ/π
) of the measured high-moist density region around the storm centre. The ultimate value of the function results in mass/energy unit, which represents the level of mass required to promote an amount of energy, within the high-density region with the N-layer. This very relationship is measured and integrated over time to give a relationship between the change of energy and mass in the high-density region within the N-layer. In a figurative sense, this high-density region appears as a “large-scale electron” compared to the nucleus of the storm, its center. Equation (3) is familiar to the spatial representation of the free particle movement in quantum chemistry, which is of non-undular quality and which is not apparently governed by the uncertainty principle 14 as applied to solve the energy of the system by the Schrödinger equation 15. Ξ brings the focus on the relationship between mass, force and rotational dynamics, where the ρ/π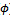 unit gives a mass/energy relationship. Because the air-pressure is ultimately affected by sea and air temperature, Ξ includes these terms as well, based on measurements.The less trivial aspect is that the relationship between air pressure and moist density is not harmonic and relies on measurements to be determined in order to conclude an approximate function, χ. The approximated function can be deduced by a series of hurricane measurement from past recordings and serve to deduce approximated functions. The function χ is thus used to add a variable to the energetic view of the storm layers as a pattern of non-harmonic behaviour, where it includes air-pressure and moist-density and assigns a principal qualitative aspect to the contemplation of the energy of the N-layer of the low-pressure system, Ξ.Because the N-layer high-density volume is continuously changing in position and density, its generalized angular momentum (as a mean value of a series of angular momenta) is used as reference for its physical quality, analogously to the angular momentum of the free particle description of the electron 16. The angular momentum of the regional density is defined by:
unit gives a mass/energy relationship. Because the air-pressure is ultimately affected by sea and air temperature, Ξ includes these terms as well, based on measurements.The less trivial aspect is that the relationship between air pressure and moist density is not harmonic and relies on measurements to be determined in order to conclude an approximate function, χ. The approximated function can be deduced by a series of hurricane measurement from past recordings and serve to deduce approximated functions. The function χ is thus used to add a variable to the energetic view of the storm layers as a pattern of non-harmonic behaviour, where it includes air-pressure and moist-density and assigns a principal qualitative aspect to the contemplation of the energy of the N-layer of the low-pressure system, Ξ.Because the N-layer high-density volume is continuously changing in position and density, its generalized angular momentum (as a mean value of a series of angular momenta) is used as reference for its physical quality, analogously to the angular momentum of the free particle description of the electron 16. The angular momentum of the regional density is defined by: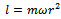
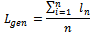 Potential EnergyThe total potential energy of the N-layer to the centre of the hurricane can be deduced by accounting for the following factors:1) Relative permittivity of the storm medium (moist).2) The electrostatic interaction between N-layers.3) The electrostatic interaction between each N-layer and the storm center (Epot) in accord with their macro-electrical charge.4) A form for the potential energy approximated by the similar expression of the potential energy of an atomic system in the form:
Potential EnergyThe total potential energy of the N-layer to the centre of the hurricane can be deduced by accounting for the following factors:1) Relative permittivity of the storm medium (moist).2) The electrostatic interaction between N-layers.3) The electrostatic interaction between each N-layer and the storm center (Epot) in accord with their macro-electrical charge.4) A form for the potential energy approximated by the similar expression of the potential energy of an atomic system in the form: 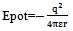 1) Relative permittivity:
1) Relative permittivity: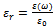
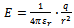
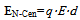
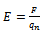
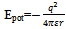 The equivalent relation for a macroscopic environment would be:
The equivalent relation for a macroscopic environment would be: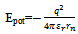 where εr is the moist permittivity constant and rn is the distance from the N-layer to the storm centre.
where εr is the moist permittivity constant and rn is the distance from the N-layer to the storm centre.  Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML