Marina Ivankova
Department of Investment Analysis, Active CIS, Moscow, 127137, Russia
Correspondence to: Marina Ivankova, Department of Investment Analysis, Active CIS, Moscow, 127137, Russia.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Evaluating the investment attractiveness of large-scale, capital-intensive projects with long-term construction period such as the Nuclear Power Plant there is a problem of analysis of factors affecting economic effectiveness and competitiveness. Generally capital-intensive projects are financed including the debt financing. Consequently during the construction stage one of the significant factors affecting the economic effectiveness of the projects is the interest during construction (IDC) which increases the capital costs of the projects and could be one of the reasons for their inefficiency and lack of competitiveness. So there is often a problem of minimizing IDC during the investment, predesign and design stages of the project. To solve this problem for a given (known or forecasted) loan conditions a mathematical economic model is offered in this article. Detailed algorithm of implementation of this model and an example of its application for the particular case are presented.
Keywords:
Interest During Construction, Optimisation of Debt Financing, Minimization IDC, Optimisation Economic Models
Cite this paper: Marina Ivankova, Mathematical Economic Model of Minimizing Interest during Construction (Example – Nuclear Power Plant), Management, Vol. 3 No. 5, 2013, pp. 273-278. doi: 10.5923/j.mm.20130305.05.
1. Introduction
The funding of large-scale, capital-intensive projects[1], such as the construction and operation and maintenance of nuclear power plants (NPP), with long-term construction and significantly deferred revenue the key problem is determine the efficiency and competitiveness of such projects and optimize a significant impact on their performance.Capital costs of NPP are about 70 percent or more of the levelized сost of electricity (LCOE), depending on the discount rate[2, 3]. Therefore, they often represent the main indicator the optimization of which is paramount in the modern world of the highly competitive NPP projects.Due to high cost of nuclear power projects in international practice the involvement of commercial loans is widespread to ensure timely financing the construction of NPP considering the deferred payment - after the start of NPP commercial operation.The result of debt financing is the rise in the cost of the project. Interests during construction (IDC) are capitalized interests, and hence increases the NPP capital costs. According to various sources, the value of IDC of new NPP can reach 15 percent or more of the total capital costs[2, 4]. Leading to a considerable increase in the cost, IDC can be the cause of economic inefficiency and lack of competitiveness of NPP compared to competitors.Problems of reduction in NPP's capital costs in the current conditions of the fierce competition in the global electricity market have received considerable attention. The leading organisations, specializing in research in the field of nuclear energy - International Atomic Energy Agency (IAEA), OECD (Organisation for Economic Co-operation andDevelopment) - Nuclear Energy Agency (NEA), Nuclear Energy Institute (NEI) and others, - also pay particular attention to reducing the cost of NPP construction.The research of analytical reports of these organisations on the problems of financing the NPP construction has shown that at the present time in the optimisation of NPP project financing considerable attention is given to the proportion of debt and equity of the NPP project, reducing investor risk during the construction period, the creation of models that determine the financial arrangement of the parties participating in the project.In addition, special attention is paid to the analysis of various sources of funds raised and their conditions: Government financing, borrowings from banks, export credit agencies, etc.[5]Optimisation of funding is also achieved through the formation of various financing schemes of NPP project[6, 7]. The existing financing schemes for reducing the financial, credit, market risks are analyzed in the reports: Build- operate-and-transfer (BOT), Build-own-and-operate (BOO), Build-and-transfer and others.Of course, all of these researches are important in solving the optimisation problem of NPP project financing and, as a consequence, in reducing the financial costs of the project. But they do not consider as a way of such reducing the optimal loans distribution among potential lenders in order to minimize the IDC.There are a number of approaches to reduce the capital cost of NPP[8]: Improve construction methods; Reduce construction schedule; Design improvement; Improve procurement, organization and contractual aspects, and others.But the reduction in capitalized IDC is not considered as one of the ways of reducing capital costs.Therefore, the urgent problem is the problem of minimizing IDC, increasing the NPP's capital costs, taking into account the known or foreseeable conditions of the loans.In our opinion, the solution to the urgent problem of optimizing NPP's capital costs should be achieved in all possible directions and take into account all the possible ways of optimizing the cost of the NPP project.Therefore, no less relevant, in our opinion, are the methods of minimizing IDC, which increase the NPP's capital costs, taking into account known or foreseeable conditions of the loans.
2. Notation and Background
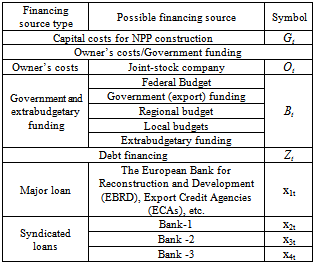
Distribution of funds for the NPP construction by year within a certain degree of accuracy is determined at different stages of the project: investment, predesign, design. On the same stage within a certain degree of accuracy the sources of financing the NPP construction are determined. These sources, first of all, are Owner’s costs, Government and extrabudgetary funding. In case of shortage of funds from these sources it is necessary to attract the debt financing from various commercial banks, credit agencies, etc. Table 1. Generalized Financing Scheme of the Investment Project
 |
| |
|
The NPP project requirement for debt financing in the t-th construction year is dictated by the lack of this year owner’s costs and/or Government and extrabudgetary funding that can provide full funding for construction in the year in accordance with the construction funding schedule.Table 1 shows the general scheme of financing the investment project[9, 10].Given the symbols of Table 1 the required loan amount is given by: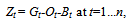 | (1) |
where n - number of years of NPP construction;Gt – sum of funds required for the construction according to the funding schedule in the t-th year;Ot – sum of Owner's costs for the construction of the t-th year;Bt - sum of Government and extrabudgetary funding for NPP construction in the t-th year.Let Zt be the element of set Z={Z1, Z2,..., Zn}. If the project needs debt financing next condition should be observed: Zt≥0 for each 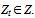 Potential lenders have the following set of parameters:{Kj, ij, Tj} for j=1...m,where m - number of potential lenders of NPP construction;Kj - power of the j-th lender - the maximum amount of funds that the j-th lender can provide as a loan for the needs of NPP construction;ij - interest rate at which the j-th lender agrees to lend to the NPP construction. The set of rates for all lenders I={i1, i2, ..., im};Tj - year from which the j-th lender can lend the loan for NPP project. That is the project can not get a loan from the j-th lender before the Tj-year. For each loan the condition should be observed:
Potential lenders have the following set of parameters:{Kj, ij, Tj} for j=1...m,where m - number of potential lenders of NPP construction;Kj - power of the j-th lender - the maximum amount of funds that the j-th lender can provide as a loan for the needs of NPP construction;ij - interest rate at which the j-th lender agrees to lend to the NPP construction. The set of rates for all lenders I={i1, i2, ..., im};Tj - year from which the j-th lender can lend the loan for NPP project. That is the project can not get a loan from the j-th lender before the Tj-year. For each loan the condition should be observed: 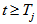 .Obviously, it is necessary to satisfy the following conditions for potential lenders to fully meet the needs of the project in debt financing:● there are considered lenders who are able to provide project funding: Kj>0 for j=1...m;● condition of nonnegativity of the interest rates: ij≥0 for each ij
.Obviously, it is necessary to satisfy the following conditions for potential lenders to fully meet the needs of the project in debt financing:● there are considered lenders who are able to provide project funding: Kj>0 for j=1...m;● condition of nonnegativity of the interest rates: ij≥0 for each ij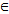 I.With the above notation proposed Table 2 summarizes the loans scheme illustrating the project.
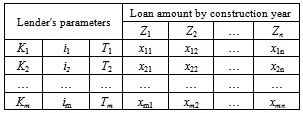
I.With the above notation proposed Table 2 summarizes the loans scheme illustrating the project.Table 2. Loans' Matrix
 |
| |
|
where xjt - required loan amount of the j-th lender in the t-th year of NPP construction. For each xjt for j=1...m, t=1...n, the condition should be observed: xjt ≥ 0. Then the set of all the required loan amount: X={xjt | xjt≥0} for j=1...m, t=1...n.
3. The Model of Minimizing the IDC
To solve the problem of loans distribution among lenders to provide financing the construction period, it is necessary that the total power of the lenders would not less of financing requirement of each year of construction, taking into account the possible timing of the loan of each lender: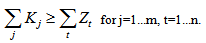 | (2) |
Obviously, the loan amounts xjt from each lender is only determined under the following conditions:● The loan amount, which is attracted from each lender, does not exceed its power: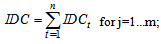 | (3) |
● The loan amount in each construction year should meet the total project needs in debt funding according to the funding schedule: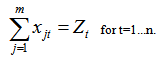 | (4) |
Let IDCt be the interest during construction period of the loan, which is taken in the t-th construction year. Then the total IDC of the project is: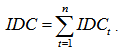 | (5) |
Then the problem of minimizing the IDC is: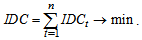 | (6) |
IDCt value is determined by the formula (7) if it is a simple interest: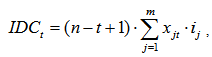 | (7) |
and by the formula (8), if it is a compound interest: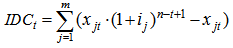 | (8) |
where (n-t+1) - period (years) during which interest is charged on loans borrowed in the t-th year before the beginning of commercial operation – stage when the repayment of loans is made due to received income (t=1...n).To solve the problem of minimizing the IDC (IDC→min) IDCt value should be minimized for t=1...n (IDCt→min). For the general case the distribution of attracted debt financing during the construction period is uneven. Therefore IDCt amount (t=1...n) is also generally uneven.IDCt value depends on the loan amount in the t-th construction year (Zt) and interest rates of lenders ij for j=1...m, at which the loan can be taken in current (t-th) year (, Kj>0). Obviously, the solution of the problem of minimizing all IDCt (t=1...n) should satisfy the condition: the more expected the loan amount in the t-th year , the more priority for setting lower interest rates for it. That is, the greater the share of loan amount, the lower should be the interest rate at it.In the distribution of loans among lenders to minimize the IDC, preference should be given in the first place to a larger Zt (t=1...n) and a lower rate ij (j=1...m).Consequently, the distribution of the loan amounts by year (Table 2) should be implemented from the larger to the lower Zt from lenders with lower interest rates ij.Let function Pmax(S, Z) order the set Z from largest to smallest, assigning to each 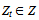 certain serial number
certain serial number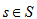 , i.e.
, i.e.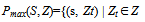 | (9) |
is the s-th largest element in set Z},where 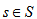 for S={1...n}.Let function Pmin(R, I) order the set I from smallest to largest, assigning to each ijI certain serial number
for S={1...n}.Let function Pmin(R, I) order the set I from smallest to largest, assigning to each ijI certain serial number 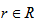 , i.e.
, i.e.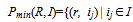 | (10) |
is the r-th smallest element in set I}, where 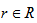 for R={1...m}. Then IDCt is a function of the form:
for R={1...m}. Then IDCt is a function of the form: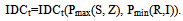 | (11) |
In view of the above, the objective function takes the form: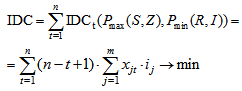 | (12) |
if IDC is calculated as simple interest (in view of (7)) or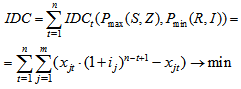 | (13) |
if IDC is calculated as compound interest (in view of (8)).The problem of finding the optimal distribution of project loan amounts for construction such a large object as NPP, for minimizing the IDC with a given loan conditions has the form of following mathematical economic model for all t=1...n, j=1...m (14):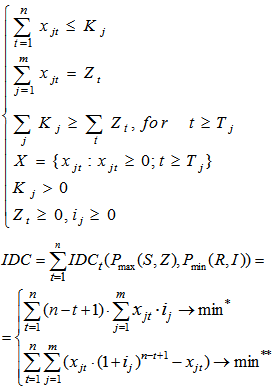 * If the IDC is calculated as simple interest** If the IDC is calculated as compound interest
* If the IDC is calculated as simple interest** If the IDC is calculated as compound interest
4. The Algorithm of Minimizing the IDC
The following algorithm of implementation the model (14) allows to determine the minimum value of IDC. The algorithm takes into account given funding schedule of NPP construction, loan conditions of potential lenders (interest rate, terms, maximum loan amount – lender’s power) and known amount of Owner’s costs and Government and extrabudgetary funding. 1. Determine the required loan amount by year of construction (formula 1)Zt=Gt-Ot-Bt, when t=1,...,n;2. Check the condition of the problem (formula 2):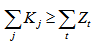 for , j=1…m, t=1…n.If condition is false, then the problem can not be solved. Otherwise go to step 3;3. Fill the loans’ matrix (see Table 2):For the first iteration:● r = 1;● s = 1;3.1) define Zt of Pmax(s, Zt);3.2) if Zt=0, then go to step 3. If Zt>0, then go to step 3.3;3.3) for t of Zt determine such ij that the following conditions are true: Pmin(r, ij); t≥Tj; Kj>0. If the conditions are true, then go to step 3.5;3.4) if at least one of the conditions step 3.3 is not true, then r=r+1 and go back to step 3.3;3.5) determine the loan amount:
for , j=1…m, t=1…n.If condition is false, then the problem can not be solved. Otherwise go to step 3;3. Fill the loans’ matrix (see Table 2):For the first iteration:● r = 1;● s = 1;3.1) define Zt of Pmax(s, Zt);3.2) if Zt=0, then go to step 3. If Zt>0, then go to step 3.3;3.3) for t of Zt determine such ij that the following conditions are true: Pmin(r, ij); t≥Tj; Kj>0. If the conditions are true, then go to step 3.5;3.4) if at least one of the conditions step 3.3 is not true, then r=r+1 and go back to step 3.3;3.5) determine the loan amount: 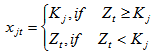 | (15) |
Correct the data: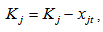 | (16) |
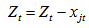 | (17) |
3.6) verify the condition 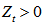 . If the condition is true, then j=j+1, r=r+1 and go back to step 3.3. Otherwise s=s+1. If s≤n, then go to step 3.1. For s>n go to step 3;4. Determine the minimum value of the objective function:4.1) if the IDC is calculated as simple interest: estimate the minimum value of IDC (formula 12);4.2) if the IDC is calculated as compound interest: estimate the minimum value of IDC (formula 13).
. If the condition is true, then j=j+1, r=r+1 and go back to step 3.3. Otherwise s=s+1. If s≤n, then go to step 3.1. For s>n go to step 3;4. Determine the minimum value of the objective function:4.1) if the IDC is calculated as simple interest: estimate the minimum value of IDC (formula 12);4.2) if the IDC is calculated as compound interest: estimate the minimum value of IDC (formula 13).
5. Example of Using the Model
Table 3. Distribution of Capital Costs, Owner’s Costs and Government and Extrabudgetary Funds, $ mln
 |
| |
|
Table 4. Examples of IDC Calculation
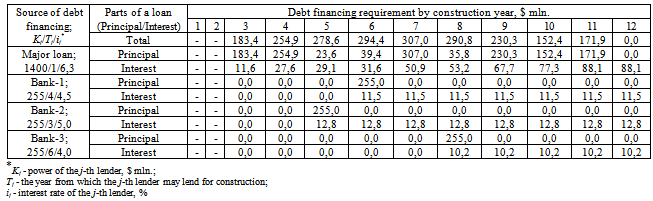 |
| |
|
Let’s consider as an example of using the model (13) for minimizing IDC for the following conditions:● distribution of capital costs of NPP construction is taken from[11];● the first, the second and the final years of NPP construction are financed by Owner’s costs. In other construction years the financing is formed by the following rules: 40% of the total amount – Owner’s costs, 20% - budgetary and extra-budgetary funds.Then the distribution of capital costs, Owner’s costs and Government and extrabudgetary funds of the NPP construction by the year have the form shown in Table 3.● as sources of debt financing the following lenders are considered:– the main creditor is able to provide for NPP construction the loan amount, which is not exceeding $1,400,000 mln. Starting from third year of construction at an interest rate of 6.3% per annum;– and three lenders are able to provide for NPP construction the loan amount, which is not exceeding $255,000 mln. each. Additional terms of the loan for each of them:Bank-1 - from the 6-th year of construction at an interest rate of 4.5% per annum;Bank-2 - from the 5-th year of construction at an interest rate of 5.0% per annum;Bank-3 - from the 8-th year of construction at an interest rate of 4.0% per annum;Each lender provides the loan under the accrual of a simple interest loan.Table 4 shows the results of evaluation of the minimum value of IDC (IDCmin) under specified conditions of lending. IDC is calculated as a simple interest (formula 11).IDCmin = $ 758,5 mln.
6. Conclusions
The proposed mathematical economic model for minimizing the IDC of NPP projects can be used for:1. optimization for IDC of existing/designed loan terms of NPP in investment, predesign and design stages;2. comparison of several options of existing/designed loan conditions of NPP projects in order to select the optimal scheme of debt financing by the minimum IDC;3. Analysis of the distribution of loan amounts and accrued IDC not only by year, but also on quarterly/monthly basis at a more detailed funding schedule or to conduct a more detailed calculation IDC. In this case it is necessary to carry out the following transformations of symbols in Table 1 and in the mathematical economic model (14):n - number of quarters/months of NPP construction;Gt - amount of funds needed to finance the construction according to the funding schedule in the t-th quarter/month;Ot - amount of Owner’s costs in the t-th quarter/month;Bt - amount of Government and extrabudgetary funds to ensure construction in the t-th quarter/month;Zt - amount of debt financing required for construction according to the funding schedule in the t-th quarter/month;Kj - the j-th lender’s power - the maximum amount of funds that the j-th lender may provide for the needs of the construction;ij – interest rate at which the j-th lender agrees to lend to the construction;Tj - quarter/month, from which the j-th lender may provide the loan;xjt – required loan amount of the j-th lender in the t-th quarter/month of construction.
References
| [1] | Nuclear energy institute. Construction work in progress: an effective. 2011.[Online]. Available:http://www.nei.org/filefolder/CWIP.pdf |
| [2] | M. Nasrullah, Elok S. Amitayani. Comparisoneof new NPP generation cost, levelized tariff and prospect of PBMR in Indonesia.[Online]. Available:http://www.batan.go.id/ptrkn/file/tkpfn16/Makalah_peserta/Kel_E/52.M.Nasrullah2,E387-394rev.pdf |
| [3] | Javier C. Palacios, Gustavo Alonso, others. Levelized costs for nuclear, gas and coal for electricity, under the Mexican scenario. Instituto Nacional de InvestigacioesNuclearres.[Online]. Available:http://www.osti.gov/bridge/servlets/purl/840500-YJxBpR/native/840500.pdf |
| [4] | Project management during NPP construction in KHNP. Korea Hydro&Nuclear Power Co., ltd. 2010.[Online]. Available:http://www.iaea.org/NuclearPower/Downloads/Technology/meetings/2010-August-19_20_WS/07.KNHP.pdf |
| [5] | The Financing of Nuclear Power Plant. NEA No.6360. OECD, 2009.[Online]. Available:http://www.oecd-nea.org/ndd/reports/2009/financing-plants.pdf |
| [6] | Nadira Barkatullah. Possible Financing Schemes for Current and Near Term Nuclear Power Projects. Department of Nuclear Energy, Planning and Economic Studies Section. [Online]. Available:http://www.iaea.org/NuclearPower/Downloadable/Meetings/2011/2011-12-05-12-09-WS-NPTD/Day-4/23_IAEA_Barkatullah-Economics_SMRDec2011.pdf |
| [7] | Investor Interest and Capacity Buildings Needs. Financing Energy Efficiency Investments for Climate Change Mitigation Project. Economic Commission for Europe. New York and Geneva, 2009.[Online]. Available:http://www.unece.org/fileadmin/DAM/energy/se/pdfs/eneff/eneff_pub/InvestorInt_CapBuilNeeds_ese32_e.pdf |
| [8] | Reduction of Capital Costs of Nuclear Power Plants. OECD. NEA, 2000.[Online]. Available:http://browse.oecdbookshop.org/oecd/pdfs/free/6600031e.pdf |
| [9] | Mazur I.I., Shapiro V.D., Olderogge N.G. Progect management: Tutorial. Second edition. - Мoscow: Omega -L, 2004 |
| [10] | Igonina L.L. Investments: tutorial - Мoscow: Infra-М, 2007 |
| [11] | Combined Application For Certificate of Environmental Compatibility, Public Convenience and Necessity And For a Base Load Review Order. Public Service Commission of South Carolina Electric and Gas Company. 2008, page 57[Online]. Available:http://www.sceg.com/NR/rdonlyres/378CF218-637D-4FDE-8636-78AE71AD1EC0/0/CombinedApplication.pdf |

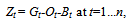
 Potential lenders have the following set of parameters:{Kj, ij, Tj} for j=1...m,where m - number of potential lenders of NPP construction;Kj - power of the j-th lender - the maximum amount of funds that the j-th lender can provide as a loan for the needs of NPP construction;ij - interest rate at which the j-th lender agrees to lend to the NPP construction. The set of rates for all lenders I={i1, i2, ..., im};Tj - year from which the j-th lender can lend the loan for NPP project. That is the project can not get a loan from the j-th lender before the Tj-year. For each loan the condition should be observed:
Potential lenders have the following set of parameters:{Kj, ij, Tj} for j=1...m,where m - number of potential lenders of NPP construction;Kj - power of the j-th lender - the maximum amount of funds that the j-th lender can provide as a loan for the needs of NPP construction;ij - interest rate at which the j-th lender agrees to lend to the NPP construction. The set of rates for all lenders I={i1, i2, ..., im};Tj - year from which the j-th lender can lend the loan for NPP project. That is the project can not get a loan from the j-th lender before the Tj-year. For each loan the condition should be observed: 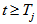 .Obviously, it is necessary to satisfy the following conditions for potential lenders to fully meet the needs of the project in debt financing:● there are considered lenders who are able to provide project funding: Kj>0 for j=1...m;● condition of nonnegativity of the interest rates: ij≥0 for each ij
.Obviously, it is necessary to satisfy the following conditions for potential lenders to fully meet the needs of the project in debt financing:● there are considered lenders who are able to provide project funding: Kj>0 for j=1...m;● condition of nonnegativity of the interest rates: ij≥0 for each ij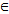 I.With the above notation proposed Table 2 summarizes the loans scheme illustrating the project.
I.With the above notation proposed Table 2 summarizes the loans scheme illustrating the project.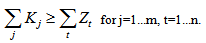
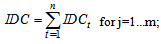
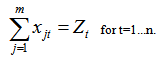
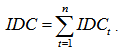
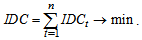
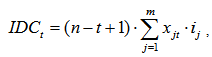
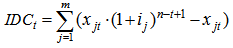
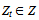 certain serial number
certain serial number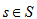 , i.e.
, i.e.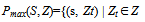
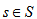 for S={1...n}.Let function Pmin(R, I) order the set I from smallest to largest, assigning to each ijI certain serial number
for S={1...n}.Let function Pmin(R, I) order the set I from smallest to largest, assigning to each ijI certain serial number 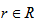 , i.e.
, i.e.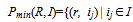
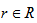 for R={1...m}. Then IDCt is a function of the form:
for R={1...m}. Then IDCt is a function of the form: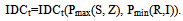
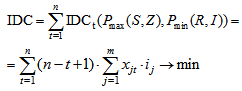
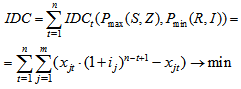
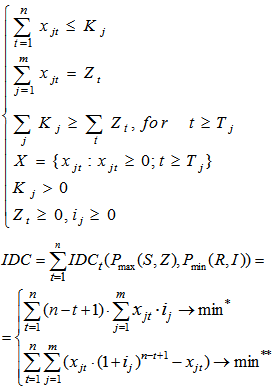 * If the IDC is calculated as simple interest** If the IDC is calculated as compound interest
* If the IDC is calculated as simple interest** If the IDC is calculated as compound interest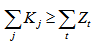 for , j=1…m, t=1…n.If condition is false, then the problem can not be solved. Otherwise go to step 3;3. Fill the loans’ matrix (see Table 2):For the first iteration:● r = 1;● s = 1;3.1) define Zt of Pmax(s, Zt);3.2) if Zt=0, then go to step 3. If Zt>0, then go to step 3.3;3.3) for t of Zt determine such ij that the following conditions are true: Pmin(r, ij); t≥Tj; Kj>0. If the conditions are true, then go to step 3.5;3.4) if at least one of the conditions step 3.3 is not true, then r=r+1 and go back to step 3.3;3.5) determine the loan amount:
for , j=1…m, t=1…n.If condition is false, then the problem can not be solved. Otherwise go to step 3;3. Fill the loans’ matrix (see Table 2):For the first iteration:● r = 1;● s = 1;3.1) define Zt of Pmax(s, Zt);3.2) if Zt=0, then go to step 3. If Zt>0, then go to step 3.3;3.3) for t of Zt determine such ij that the following conditions are true: Pmin(r, ij); t≥Tj; Kj>0. If the conditions are true, then go to step 3.5;3.4) if at least one of the conditions step 3.3 is not true, then r=r+1 and go back to step 3.3;3.5) determine the loan amount: 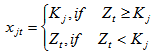
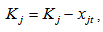
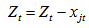
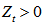 . If the condition is true, then j=j+1, r=r+1 and go back to step 3.3. Otherwise s=s+1. If s≤n, then go to step 3.1. For s>n go to step 3;4. Determine the minimum value of the objective function:4.1) if the IDC is calculated as simple interest: estimate the minimum value of IDC (formula 12);4.2) if the IDC is calculated as compound interest: estimate the minimum value of IDC (formula 13).
. If the condition is true, then j=j+1, r=r+1 and go back to step 3.3. Otherwise s=s+1. If s≤n, then go to step 3.1. For s>n go to step 3;4. Determine the minimum value of the objective function:4.1) if the IDC is calculated as simple interest: estimate the minimum value of IDC (formula 12);4.2) if the IDC is calculated as compound interest: estimate the minimum value of IDC (formula 13). Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML


