-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Management
p-ISSN: 2162-9374 e-ISSN: 2162-8416
2012; 2(4): 96-105
doi: 10.5923/j.mm.20120204.03
Multi Criteria Governmental Crop Planning Problem: An Analytic Hierarchy Approach
Salah R. Agha. Latifa G. Nofal , Hana A. Nassar , Rania Y. Shehada
School of Industrial Engineering, Islamic University of Gaza, Gaza, Occupied Palestinian territories
Correspondence to: Salah R. Agha. Latifa G. Nofal , School of Industrial Engineering, Islamic University of Gaza, Gaza, Occupied Palestinian territories.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
The goal of this study is to rank crops to cultivate in the governmental agricultural lands in Gaza Strip using AHP methodology as a Multi Criteria Decision Making (MCDM) tool. This study is applied under the normal condition, from the governmental point of view. Seven main criteria were first identified consisting of economical, financial, marketing, environmental, technical, political, and social criteria, while thirty one sub-criteria were then identified. Crops were divided into eight types that include vegetables, fruits, citrus, olives, palms, export crops, field crops and medical and aromatic crops. The results indicate that the economic criteria are the most important criteria as they represent 0.33 of the total weight, while the technical criteria are the least important criteria as they represent 0.07 of the total weight. Sub-criteria weights indicate that the contribution to GDP sub-criterion is the most important one with respect to the goal as it has 0.103 of the total weight. Cropping pattern is skewed towards export crops, citrus and vegetables.
Keywords: AHP, Analytical Hierarchy Process, Crop Planning, MCDM, Multi Criteria Decision Making, Governmental, Ranking, Co-Plot, Agriculture
Article Outline
1. Introduction
- Crop planning plays a vital role in agricultural sector. Many problems associated with agriculture such as soil fertility, seasonality, productivity fluctuations can be controlled by successful crop planning. The Ministry Of Agricultural (MOA) in Gaza Strip attempts to develop a crop plan as an effective agricultural strategy to deal with agricultural problems. This study aims to help MOA make a strategic decision of selecting the most proper crops to cultivate. As opposed to the resistant economy condition which is mainly characterized by the siege imposed on Gaza Strip after 2006[1], this paper focuses on treating the crop planning problem in Gaza Strip under the normal economy condition which prevailed Gaza Strip before 2006. Normal economy is characterised by the following:• Imports and exports are allowed. • Production inputs are available. • There are surpluses in some crops and shortages in others.• MOA focused on cultivating crops that greatly contribute to Gross Domestic Product (GDP) and can face competition between local and foreign crops due to its high quality characteristics. The process of developing a suitable and effective crop plan is a complex decision making problem involving multiple objectives. The purpose of this paper is to rank thecrops according to the certain criteria, using Analytic Hierarchy Process (AHP).The selection of AHP in this study is due to its ability to structure a problem hierarchically, thus; it provides users with a better focus on specific criteria and sub-criteria when allocating the weights. Furthermore, qualitative and quantitative criteria can be evaluated on the same preference scale of nine levels[2]. This study is motivated by the following:• The previous studies[3-14] focused on resources consumption criteria such as land, water, fertilizers, labor…..etc., while this study considers many other criteria to develop effective long term crop plan, such as self sufficiency, food security, intercropping, organic agriculture, postharvest storage and many other criteria as will be illustrated through this study.• More criteria are considered in this study.• The agricultural sector in Gaza Strip has many problems that are not typical in related literature.In this paper, sections are organized as follows: section two reviews the literature on crop planning, followed by AHP methodology in section three, section four presents crop planning in Gaza Strip followed by the model application in section five. Results and analysis are given in section six followed by conclusions in section seven.
2. Literature Review
- Cropping decisions mainly involve determining the crops to be cultivated and the area to be planted for each crop. The crop planning issue is usually formulated as a single objective linear programming model. However, at a regional level and in term of sustainable agricultural development, crop planning pursues multiple objectives where each objective has to be monitored and measured using the appropriate criteria. Many papers have been written on this subject.[3,4] suggest the methods of multi-objective programming for land use in regional level.[5] considers a nation-wide crop-planning problem, formulates the problem as a goal program and discusses the importance of three different goals for a case problem.[1] uses an integrated AHP- PROMETHEE approach to solve the crop planning problem under two conditions: the normal economy condition and the resistant economy condition.[6] builds a model including multiple crops, market and nonmarket crop uses, and seasonality in production, consumption, and labor supply.[7] uses a multi-objective programming approach to examine the possibilities of simultaneously achieving environmental goals such as the reduction of agrochemical and irrigation water use as well as acceptable farm incomes.[8] uses multi-objective programming modeling and solved crop planning problems for optimal production of several seasonal crops in a planning year.[9] develops a model that focused on attaining three objectives simultaneously, namely, profit maximization, employment maximization and erosion minimization. Results of the model indicated that, when compared with the current cropping structure, the implementation of the optimal cropping pattern could increase profit and employment and decrease soil erosion significantly.[10] proposes a mathematical model for optimal cropping patterns under water deficits in dry regions. They identified both the total area and the irrigation level allocated to a given selected crop taking into accounts the possible successors and predecessors of this crop. Both annual and seasonal crops were examined in the same study.[11,12] present how fuzzy goal programming can be efficiently used for modeling and solving land-use planning problems in agricultural systems for optimal production.[13] develops a fuzzy multi-objective linear programming model for solving the multi-lever and multi species production of edible fungus circular economy system decision problem in a fuzzy environment.[14] develops Linear programming and fuzzy optimization models for planning and management of available land-water-crop system of Mahanadi-Kathajodi delta in eastern India. The models were used to optimize the economic return, production and labor utilization, and to search the related cropping patterns and intensities with specified land, water, fertilizer and labor availability, and water use pattern constraints.
3. Analytic Hierarchy Process
- Analytic Hierarchy Process (AHP) is one of multi criteria decision-making methods; it was originally developed by Thomas L. Saaty in the mid 1970s. It combines tangible and intangible aspects to obtain the priorities associated with the alternatives of the problem. AHP is a structural framework that allows decision-makers to model a complex problem in a hierarchical structure by breaking it down into smaller parts, then calling for a simple comparison with respect to pairs of judgments to develop priorities within each level of hierarchy. Finally, results are synthesized to obtain overall weights of the alternatives. The input can be obtained from actual measurement such as price, weight etc., or from subjective opinion. AHP has been applied in many and diverse areas of decision-support. These applications involve: Selection[15]; allocation[16]; evaluation and benchmarking[17]; ranking and prioritization[18-20]. The AHP methodology is explained in the following steps.
3.1. Hierarchical Structuring of the Problem
- The first step of AHP is to develop the hierarchical structure representing the problem at hand. A general form of AHP structure is presented in Figure 1. In the simplest case, the hierarchy has three levels. The first level represents the goal of the decision problem and is analyzed as resulting from the aggregation of evaluation criteria represented by the second level; the last level of the hierarchy involves the alternatives to be evaluated. In more complex cases, there may be more levels, corresponding to splitting criteria into sub-criteria.
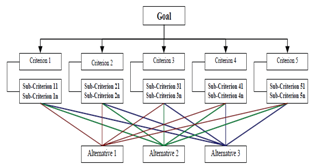 | Figure 1. AHP Hierarchy,[17] |
3.2. Performing Pairwise Comparisons
- Once the hierarchy of the problem is defined, the decision-maker performs a series of pairwise comparisons within the same hierarchical level and then between sections at a higher level in the hierarchy structure to have n*(n-1)/2 comparisons if there are n criteria. In comparisons, a ratio scale of 1-9 is used to compare any two elements. Table 1 shows the measurement scale defined by Saaty[21].The pairwise comparisons of various criteria are organized into a square matrix A(aij)where a ij = wi /wj and i, j =1,2...,n. The diagonal elements of the matrix are 1. The criterion in the ith row is better than criterion in the jth column if the value of element (i, j) is more than 1; otherwise the criterion in the jth column is better than that in the ith row. The (j, i) element of the matrix is the reciprocal of the (i, j) element.
3.3. Synthesis
- Once judgments have been entered for each part of the model, the rating of alternative is multiplied by the weights of the sub-criteria and aggregated to get local ratings with respect to each criterion. The local ratings are then multiplied by the weights of the criteria and aggregated to get global ratings. The AHP produces weight values for each alternative based on the judged importance of one alternative over another with respect to a common criterion. The results are then synthesized to obtain rank of the alternatives in relation to the overall goal.
3.4 Consistency Evaluation
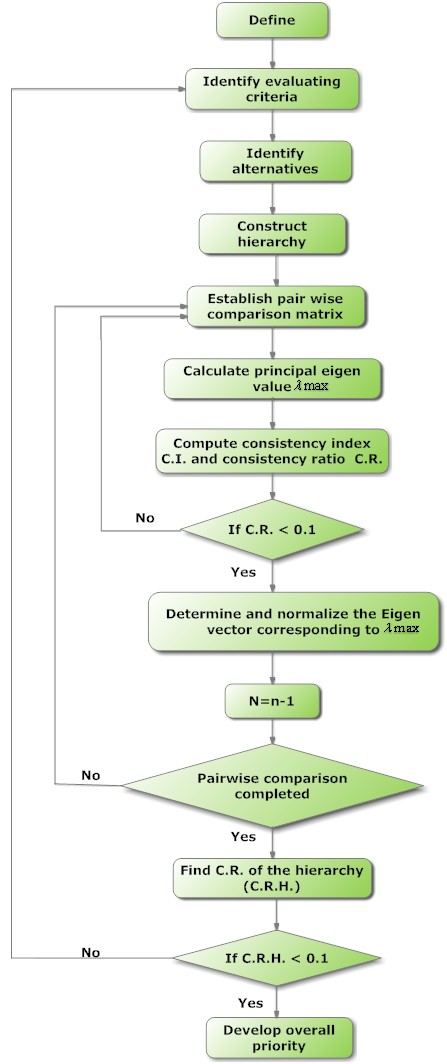 | Figure 2. Process of AHP[By researchers] |
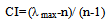 | (1) |
|
4. Crop Planning in Gaza Strip
- The MOA divided agricultural history in Gaza Strip into four stages according to major political events that occurred in the region[22]. Every political stage has a very clear impact on agriculture. The four stages are: • Period between 1948-1967: In this period, Palestinian agriculture focused on citrus which was the first strategic crop, where production was for local and external market. The problem was the citrus consumes large amounts of water which led to a sever shortage of the aquifer water. Furthermore it consumes nutrients from soil. • Period between 1967-1994: In this period, the Israeli citrus competed against Palestinian citrus, which required raising the quality standards for Palestinian exported citrus; therefore, farmers tended to farm larger areas of vegetables instead of citrus. At the end of 1970s, vegetables became the first strategic crop. Vegetables consume more water than citrus, which aggravated the problem of water shortage.• Period between 1994-2006: The agricultural policies were the same as the period from 1967-1994. The Palestinian agricultural economy was adversely affected by Paris Economic Agreement, through imposing restrictions on exports and imports. This period is characterized by greater consumption of water through focusing on the cultivation of export crops (strawberry, carnation flowers, pimento .....) which increase the water shortage problem. • Period between 2006- until now: In this period, MOA re-read the agricultural policies. The agricultural resistant economy concept was coined, where the attention began to turn to crops that can face the existing problems including water shortage, lack of production inputs and the unemployment.
5. Application
- Figure 3 shows the road map that the researchers followed to reach the research goal. Starting with goal definition, then data collection, in which, criteria and alternatives are identified, ending with AHP model application and verification. The first step in multi-criteria decision making, regardless of the selected method, is the identification of the alternatives and the relevant criteria. The considered alternatives and criteria were identified through: 1. Literature review. 2. The policies of MOA in Gaza Strip. 3. Interviews with experts and agricultural engineers from the MOA and some associations such as the society of agricultural relief and the institute of environmental research.
5.1. Criteria, Sub-Criteria and Alternatives Identification
- For the crop planning problem under study, there are seven main criteria that include: economic, financial, marketing, environmental, technical, political and social criteria. These criteria are split into thirty one sub-criteria. Final criteria were adopted after presenting them to experts and engineers from the MOA and some agricultural societies. This was done using a questionnaire, where experts were asked to add, delete or combine some criteria, sub-criteria and alternatives. Nationwide, there are many classifications of crops (alternatives). In this study, crops are classified in such a way that enable experts to compare between them according to the considered criteria. Therefore, crops with similar characteristics are grouped in one alternative. Final types of crops were adopted after presenting them to experts using the questionnaire used to define criteria. Experts were asked to give their opinion about the classification of crops, and most of them agreed with the researchers' classification. It is noted that, somewhat, this classification of crops is often used by the MOA. After identifying criteria, sub-criteria and alternatives, a hierarchy of four levels, was constructed as shown in Figure 4.
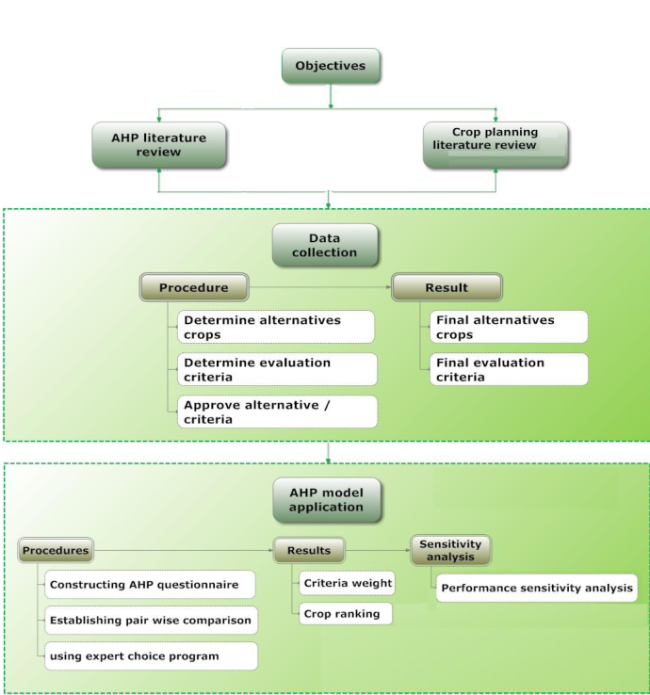 | Figure 3. Study methodology |
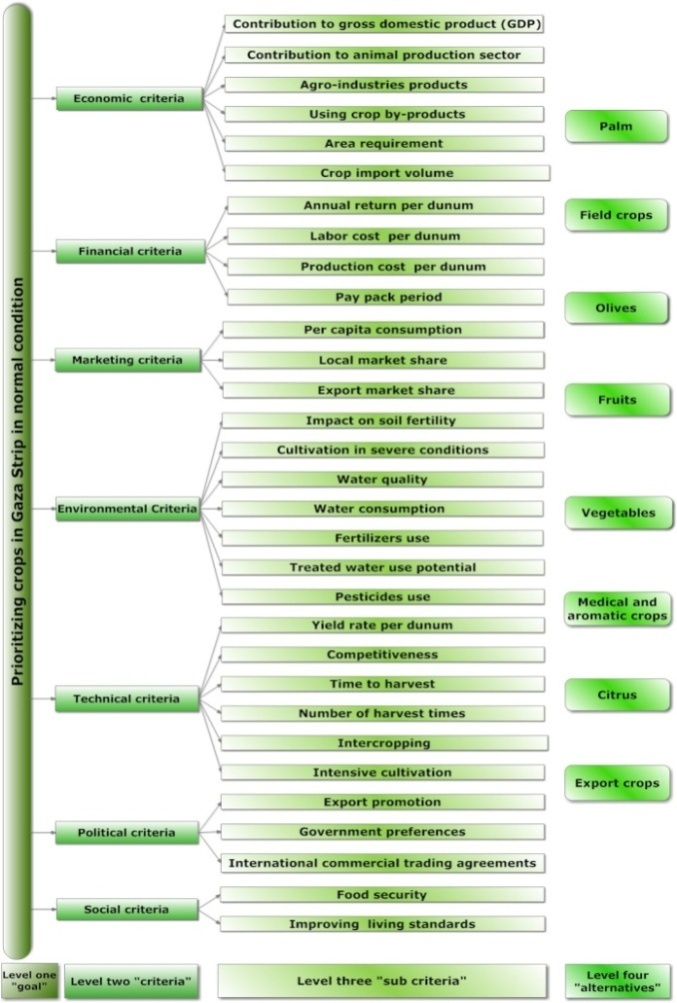 | Figure 4. AHP hierarchy for crop planning problem |
5.2. Establishing the Pairwise Comparison Matrix
- To conduct the pairwise comparison, a questionnaire was designed and distributed among nine agricultural experts. In this questionnaire, the experts were asked to assign a score from one to nine for each pairwise comparison. The questionnaire was designed in a way to help experts to fill it easily. This was made using a simple example given in the cover page of the questionnaire. Since AHP is not a statistical tool; there is no rule that defines the number of experts to fill the questionnaire.After receiving the questionnaires from experts, the CR of each questionnaire was calculated. It was observed that some of the pairwise comparisons have CR values larger than 0.1, which meant that they are inconsistent. Therefore, experts were asked to refill questionnaire again after they were told about the inconsistencies.
5.3. Obtaining Final Weights
- Once the judgments of each of the nine experts were obtained and tested for the consistency, the average for each comparison was computed to get the final comparison matrices. The average scores were entered to Expert Choice 11 (E.C 11.5)[23]. The criteria and sub-criteria weights are shown in Table 3.
6. Results and Analysis
6.1. Criteria Results
- Figure 5 shows the weights of the seven main criteria with respect to the goal. The results indicate that economic criterion is the most important one as it represents 0.33 of the total weight. Environmental criterion comes second represents 0.15 of the total weight, whereas technical criterion ranks the lowest among these criteria as it scored 0.07 of the total weight. Marketing and financial criteria equally contribute to the goal for a weight of 0.13. The fact that economic criterion has the highest weight reflects the tendency of the MOA to cultivate the crops that greatly contribute to the GDP to increase the contribution of the agricultural sector to GDP.
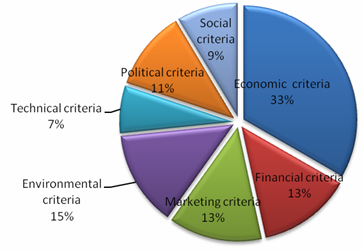 | Figure 5. Average relative weights of the criteria with respect to the goal |
6.2. Final Crop Weight
- The rank of crops, according to AHP method, is shown in Figure 6. Export crops have the highest relative weight (0.18). Vegetables and citrus have the second priority, followed by olives then fruits and field crops with the same priority, then palms and medical crops come in the last.
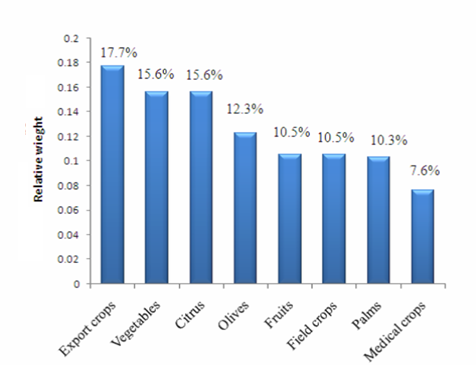 | Figure 6. Relative weights and ranking of the alternatives with respect to the goal |
6.3. Sensitivity Analysis
- The sensitivity analysis of the performance of alternatives with respect to each main criterion is shown in Figure 7. From this graph, it is noted that export crops have the highest performance score with respect to all criteria, except the environmental criterion, it has the lowest performance score with respect to this criterion. While vegetables have the second top performance score with respect to all criteria excluding the environmental criterion, and it has better performance score on environmental criterion than the export crops. The performance of the other crops swings among the main criteria. Fruits appear to have moderate performance on all criteria. To have more insights into the performance of the different alternatives with respect to criteria, the original evaluation matrix ‘X8×7’ was submitted to co-plot software. Co-plot is used to locate each alternative in a two-dimensional space in which the location of each action is determined by all criteria simultaneously. The input for this software is the evaluation matrix (alternatives versus main criteria). The co-plot method produces three results:1. similarity among actions by the composite of all criteria involved.2. the structure of correlations among the criteria.3. the mutual relationship between the actions and the criteria[24].
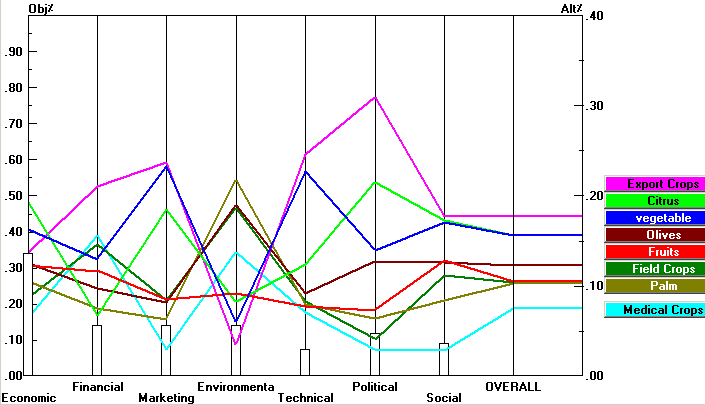 | Figure 7. The performance graph for the crops under study |
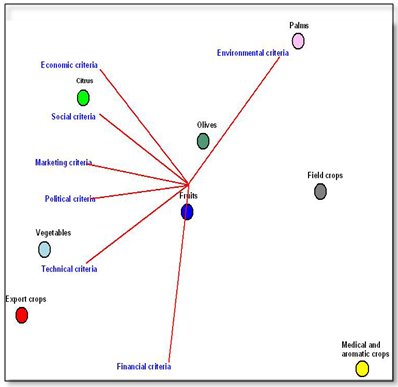 | Figure 8. Co-plot graphic display of crops and the evaluation criteria |
7. Conclusions
- Crop planning model in this study is constructed as a MCDM problem in order to compare eight types of crops using AHP methodology. There are many factors that affect the selection of crops. The study considered seven main criteria and thirty one sub criteria, which could help in developing better decisions. The results show that The economic criteria are the most important criteria as they represent 0.33 of the total weight, while the technical criteria are the lowest important criteria as they represent 0.07 of the total weight. The final AHP rank of crops shows the most important crops are export crops, citrus and vegetables, which means that cropping pattern is skewed towards these crops.Based on the results of this study, some points are recommended for future studies:• Since goal programming (GP) provides better insights to the problem, our immediate plan is to build a GP model to determine the area of each crop to be cultivated. • Dealing with crops as groups forced the researchers to approximate data. To have more accurate results, it is recommended for future work to apply this study taking crops as individuals.• Since each element in the AHP hierarchy must be independent, other MCDM method as Analytic Network Process (ANP) can be used to deal with the dependency that could be found between some criteria.This study is performed on the governmental agricultural lands in Gaza Strip from the governmental view, the agricultural private sector is not included so, the farmers view is not considered. It is recommended to consider the farmers view in other future studies.
|
ACKNOWLEDGEMENTS
- The authors wishes to thank Engineer Balsam El-Nafar for her help in data collection and analysis. Besides, authors offer their thanks to the Scientific Research Deanery at the Islamic University of Gaza for their financial support to complete this study.
References
| [1] | Agha, S.R, Nofal, L, and Nassar, H. (2011) ‘Multi criteria governmental crop planning problem based on an integrated AHP-PROMETHEE approach’, International journal of applied management science, accepted. |
| [2] | Albadvi, A., Chaharsooghi, K. and Esfahanipour, A. (2007) ‘Decision making in stock trading: an application of PROMETHEE’, European Journal of Operational Research, Vol. 177, No. 1, pp.673–683. |
| [3] | Miao, C., He, B. and Chen, X.(2006) ‘Study on the multiple objective linear planning applied in comprehensive control of small watershedła case study from mimagou small watershed in shizhu county,sichuan province’, Chinese Journal of Eco-Agriculture, Vol.(14), No.(3), pp. 223–227. |
| [4] | Yu, S. and Zhang, J.(2006) ‘Multi-objective programming method for land use based on genetic algorithm’, China Population, reaources and enviorment, Vol.(16), No.(5), pp. 62-66. |
| [5] | Sarker, A. and Quaddus, A. (2002) ‘Modeling a nationwide crop planning problem using a multiple criteria decision making tool’, Computers and Industrial Engineering, Vol. 42, Nos. 2–4, pp.541–553. |
| [6] | Lee, D., Tipton, T. and Lang, P.(1995) ‘Modelling cropping decisions in a rural developing country:a multiple-objective programming approach’, Agricultural Systems, Vol.(49), No.(1), pp. 101-111. |
| [7] | Ragkos, A. and Psychoudakis, A. (2008) ‘Minimizing adverse environmental effect of agriculture: a multi-objective programming approach’, Operation Research International Journal, Vol. 9, No. 3, pp.267–280. |
| [8] | Wei, W., Liu, Y., Hu, Z. and Zhao, Y. (2009) ‘An optimal model of dry land multiple-cropping circular economy systems’, World Journal of Modeling and Simulation, Vol. 5, No. 3, pp.203–210. |
| [9] | Mohaddes, A. and Mohayidin, G. (2008) ‘Application of the fuzzy approach for agricultural production planning in a watershed, a case study of the Atrak watershed, Iran’, American-Eurasian Journal of Agricultural and Environmental Science, Vol. 3, No. 4, pp.636–648. |
| [10] | Haouari, M. and Azaiez, M. (2001) ‘Optimal cropping patterns under water deficits’, European Journal of Operation Research, Vol. 130, No. 1, pp.133–146. |
| [11] | Biswas, A. and Pal, B. (2005) ‘Application of fuzzy goal programming technique to land use planning in agricultural system’, Omega, Vol. 33, No. 5, pp.391–398. |
| [12] | Gupta, A., Harboe, R. and Tabucanon, .(2000) ‘ Fuzzy multiple-criteria decision making for crop area planning in narmada river basin’, Agricultural Systems, Vol. 36, No. 1, pp.1-18 |
| [13] | Zhao, Y., Wang, J., Zheng, L. and Hu, Z. (2009) ) ‘A multi-objective model of the edible fungus circular producing under fuzzy environment’, World Journal of Modeling and Simulation, Vol. 5, No. 4, pp.252-260. |
| [14] | Sahoo, B., Lohani, K. and Sahu, K. (2006) ‘Fuzzy multiobjective and linear programming based management models for optimal land-water-crop system planning’, Water Resources Management, Vol. 20, No. 6, pp.931–948. |
| [15] | Hambali A., Sapuan S.M., Ismail N., and Nukman Y., (2009) ‘Composite manufacturing process selection’, International Journal of Mechanical and Materials Engineering, Vol.4, No. 1, 49 -61. |
| [16] | Steven, V. (2008) ‘Asset allocation: an application of the analytic hierarchy process’, Journal of Business & Economics Research, Vol. 6, No. 9, pp. 87–94. |
| [17] | Agha, S. R. (2008) ‘Evaluating and benchmarking of nongovernmental training programs: an analytical hierarchy approach’, Jordan Journal of Mechanical and Industrial Engineering, Vol. 2, No. 2, pp. 77-84. |
| [18] | Babic, Z. and Palzibat, N. (1998) ‘Ranking of enterprises based on multicriterial analysis’, International Journal of Production Economics, Vol. 56–57, No. 1, pp. 29–35. |
| [19] | Ahmet, B. and Bozbura, F. (2007) ‘Prioritization of organizational capital measurement indicators using fuzzy AHP’, International Journal of Approximate Reasoning, Vol. 44, No. 1, pp. 124–147. |
| [20] | Agha, S. R., Jarbo, M.,and Matr, S. (2012) ‘A multi-criteria multi-stakeholder industrial projects prioritization in Gaza Strip’. Arabian Journal of Science and Engineering ,accepted. |
| [21] | Saaty, T.L. (1980) The Analytic Hierarchy Process, McGraw-Hill, New York. |
| [22] | Ministry of Agriculture (MOA) (2009), Annual Report for 2010, available at http://www.moa.gov.ps/PDFFiles/Annualreportof2010.pdf (accessed on 5 September 2010). |
| [23] | Expert Choice Inc. (2004) Expert Choice, Expert Choice Software and Manual, 4922 Ellsworth Ave., Pittsburgh. |
| [24] | Raveh, A. (2000) ‘Co-plot: a graphic display method for geometrical representations of MCDM’, European Journal of Operational Research, Vol. 125, No. 1, pp.670-678. |
| [25] | Pedhazur, J. (1997) Multiple Regression in Behavioral Research, Harcourt-Brace, New York. |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML