Elias Kassahun Woldeselassie1, 2, Chi Xiuwen1, Dereje Demissie Aredo1
1School of Resource and Environmental Engineering, Wuhan University of Technology, Wuhan, China
2Department of Mining Engineering, Bule Hora University, Oromia, Ethiopia
Correspondence to: Elias Kassahun Woldeselassie, School of Resource and Environmental Engineering, Wuhan University of Technology, Wuhan, China.
| Email: |  |
Copyright © 2021 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
The primary purpose of blasting is to fragment rock, and there are significant rewards for delivering a fragmentation size range that is not only well suited to the mining system it feeds, but also minimizes unsaleable fractions and enhances the value of what can be sold. The outcome of blasting operations is determined by a number of indices or parameters, which can be either controllable or uncontrollable. Methodologies employed in this paper includes mathematical calculation, literature survey, and direct field observations for obtaining specific parameters necessary for analyzing and estimating the size distribution of rock fragments based on Kuz-Ram and Modified Kuz-Ram fragmentation models. We take Direct measurement from Derba Midroc Cement factory which is in Ethiopia's Oromia region of spacing, such as burden, hole depth and stemming length of blastholes. The measurement has been done in the field by using tape measure and the results were recorded in a field note book. The type of explosives used per shot, charging techniques, stemming materials, and fragmentations were all observed directly from the field and photographed for illustrations.
Keywords:
Kuz-Ram, Modified Kuz-Ram, Fragmentation, Drilling, Blasting
Cite this paper: Elias Kassahun Woldeselassie, Chi Xiuwen, Dereje Demissie Aredo, Optimization of Drilling and Blasting by Empirical Modelling Specifically Kuz-Ram and Modified Kuz-Ram Model at Midroc Derba Limestone Quarry Site, Derba, Oromia, Ethiopia, International Journal of Mining Engineering and Mineral Processing , Vol. 10 No. 1, 2021, pp. 1-8. doi: 10.5923/j.mining.20211001.01.
1. Introduction
Blasting is the primary stage of rock size reduction after drilling and it is followed by crushing and grinding actions on the comminution system. The main objective of blasting action in the mine is to produce a fragmented rock with sizable and cost-effective way. During blasting the blaster man should consider the geology of the blasted rock, the cost of drilling, proper use of explosive, the size of the fragmented rock, and so on. The outcome of blasting operations is determined by a number of indices or parameters, which can be either controllable or uncontrollable. The controllable parameters are basic blast design parameters, which can be varied to adjust the outcome of the operations, and this product provides close to accurate results assuming the rock mass is homogenous and without discontinuities. However, since the uncontrollable ones are inherent properties of the rock, geological structures, which are often defined by fracture distributions, need to be factored and included into the blast design. According to (Hustrulid, 1999), the controllable parameters are classified in the following groups:• Geometric: Diameter, charge length, burden, spacing, etc. • Physicochemical or pertaining to explosives: Types of explosives, strength, energy, priming systems, etc. • Time: Delay timing and initiation sequence. Whereas the uncontrollable factors include, but are not limited to, geology of the deposit, rock strength, and properties, presence of water, joints, etc.Drilling and blasting are the critical and important operations of every hard rock mine, contributing up to 25% of the overall mining cost in some mining operations. However, optimization of the cost of the mine is mainly consider drilling and blasting. If we consider these as a part of optimization, we can reduce the overall production cost of the mine. In order to minimize the cost of drilling and blasting, we have to model and predict the size of fragmentation. There are two broad classifications that help in modeling the fragmented rock. These are empirical modeling and mechanistic model. Empirical modeling infers finer fragmentation from higher energy input, while mechanistic modeling tracks the physics of detonation and the process of energy transfer in well-defined rock for specific blast layouts, deriving the whole range of blasting results. When compared to mechanistic modeling, empirical modeling is one of the most reliable and easy-to-use. The mechanistic modeling is very difficult to get adequate data and it needs a long time to analyze it; as a result, it is difficult to apply in day-to-day activity. however, empirical modeling is easy to garner data and takes into account the geological property of the rock mass as well. Some of these models pertaining to surface blasting include the Bond-Ram model, Kou-Rustan equation, Energy Block Transition (EBT) model, Swedish Detonic Research Foundation (SveDeFO) model, Kuz-Ram model, Larson model, Rosin-Rammler model, Kuznetsov-Cunningham-Ouchterlony (KCO) model, Chung and Katsabanis model, Modified Kuz-Ram model, Crushed Zone Model (CZM), Two Component Model (TCM), Artificial Neural Networks (ANN) and many more (Kanchibotla et al., 2001; Ouchterlony, 2005; Kazem and Bahareh, 2009 and Vamshidhar and Venkatesh, 2010). Among these empirical modeling, the Kuz-Ram model is popular to use since it is applicable for metal mine as well as industrial mines such as limestone and it has a direct linkage between blast design and fragmentation results (Cunningham, 2005). The Kuz-Ram model developed by Cunningham; is the most common model used in estimating heap size distribution after blasting (1987). Cunningham integrated the empirical equation proposed by Kuznetsov (1973) for average size (x50) estimation with the size distribution function proposed by Rosin and Rammler (1933). Actually, the Kuz-Ram model by itself has its own shortcoming. The first one is that does not consider fine region and the second is that it does not consider accurate timing or delay offered by modern electronic detonators.This work is focused on the optimization of drilling and blasting parameters by predicting the rock fragmentation by using the Kuz-Ram model in DERBA MIDROC CEMENT PLC (DMC), DERBA, OROMIA, ETHIOPIA.DMC, an Ethiopian subsidiary of Midroc Group, is setting up a 5,600 tone per day (tpd) capacity clinkerisation plant in the vicinity of the Derba town near Central Region of Federal Democratic Republic of Ethiopia, Addis Ababa. The limestone which shall constitutes the main raw material for the proposed clinkerisation project is proposed to be supplied from the Mugher limestone deposit, located about 8 km southeast of the proposed plant site. Apart from limestone, this deposit shall also source the marl, required as corrective material for cement manufacture, which by virtue occurs as overburden to limestone. DMC has obtained mining permit for an area of 189.90 hectares for exploitation of the Mugher limestone/ marl deposit.
2. Location
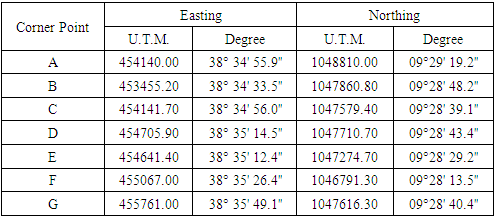
The Mugher limestone deposit and other raw material resource areas are located 110 km to the NNW of Addis Ababa in the Federal Democratic Republic of Ethiopia. The limestone deposit has been named after the village Mugher, where it is located. The location of the Mugher limestone deposit is shown in with the coordinates. The coordinates of the limestone deposit are given in Table 1.Table 1. Coordinates of the corners of Mugher Limestone Deposit
 |
| |
|
3. Accessibility
The Mugher limestone deposit is accessible by road from Chancho, which is the nearest major town on National Highway leading to Debre Markos from Addis Ababa. Chancho town falls under Northern Shoa zone of Oromia region and is situated approximately 40 km north of Addis Ababa. From Chancho town the limestone deposit can be accessed by graveled road via Mulo Segno Gebeya, Welenkomi and Wegidi villages for a total distance of 70 km. On the way to Derba village from Chancho town, a graveled road branches off at 13.5 km distance towards the south west direction, after Mulo Seya village, which leads to Segno Gebeya (locally known as “Mulo”) village located approximately at a distance of 15.5 km from the 13.5 km bifurcation point. From Segno Gebeya village a dry weather trail leads to Welenkomi village in northwest direction. Further from Welenkomi village, the trail leads to Wegidi village in northeast direction and from Wegidi the trail leads to Mugher valley limestone deposit in east direction. The total distance from Segno Gebeya village to the deposit is 41 km. Alternatively the Mugher limestone deposit can also be approached through Derba village, which lies 24 Km NW of Chancho town. The deposit lies further NW of Derba village at a crow fly distance of 9 Km and can be accessed through ropeway operated by Mugher Cement Enterprise. However, the limestone from the deposit shall be transported to plant through conveyor belt.
4. Geology
4.1. Regional Geology
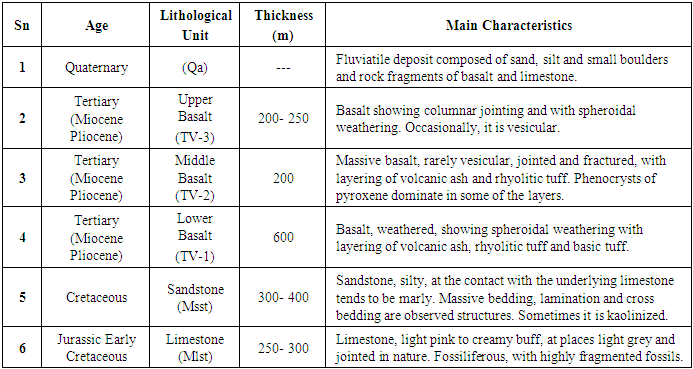
In early Mesozoic era, the eastern part of Africa was marked by the first transgression of the Indian Ocean, reaching its upper development in early upper Jurassic, after which regression due to uplifting followed. Due to these, transgression followed by regression, three major lithological divisions were recognized. These major lithological divisions are Adigrat sandstone, Antalo limestone and upper sandstone. On top of the Mesozoic rocks the volcanic rocks of Trap basalt rest unconfirmably. According to Mohr (1962) the area is classified as follows.Ø Tertiary – Trap Basalt SeriesØ Cretaceous or Upper Jurassic – Upper SandstoneØ Upper Jurassic – Antalo LimestoneØ Middle Jurassic - Adigrat Sandstone (Lower Sandstone)The age of all litho units ranges between 140 to 200 million years. The rock formation of region is consisting of basement complex rocks of strongly folded gneisses and metasediments, schist and marble. The area consists of different rocks from Mesozoic sedimentary to Tertiary volcanic rocks. At the top, Mugher river and its tributaries cut deep into the volcanic plateau of basalt and tuff units. Under the basalt and tuff, the Mesozoic rocks which comprise of Ambaradom sandstone, Antalo limestone and gypsum/ shale units are exposed. A generalized lithological sequence, from youngest to oldest, occurring within and outside the lease area is presented in the following table.Table 2. Geological Sequence of Concession area
 |
| |
|
4.2. Local Geology
The local geology of the area as interpreted from the boreholes is as follows:- Top soilThe entire lease hold area is concealed under a thick soil cover. The overburden/ top soil as encountered in the boreholes drilled, mainly composed of black cotton soil/ marly sediments along with sand and rolled fragments of basalt. The average thickness of this lithounit varies from 0.25m to 6.80m.- Marl/Marly limestoneThis litho unit is overlain by top soil/ overburden soil. Marl is basically off white to pale yellow argillaceous calcareous sediments, soft and compact. This unit is often intercalated with thin beds of limestone and hence marl with thin beds of limestone is termed as “marly limestone”. In few of the boreholes, shale and sand layers were also noticed within this horizon. Gypsum and gypsiferous shale are confined within this horizon.- Gypsum / Gypsiferous shaleThis lithounit is mainly confined within marl and marly limestone horizon. Gypsum is white to off white in colour intercalated with shale which is dull and pale in colour. Gypsum and gypsiferous shale have alternating sequence. Thin partings/ stringers of gypsum were noticed in other litho units encountered in the boreholes. The average thickness of this horizon is about 19m.- LimestoneThis litho unit is overlain by marl and marly limestone horizon. The limestone beds as encountered in the borehole are compact, crypto crystalline, fossiliferous with some brachiopod and pelecypod shell fragments. It is light grey to creamy brown in color. The limestone beds are often intercalated with the layers of gypsum, gypsiferous shale and shale. The average thickness of this unit is about 35m.- Siliceous limestone / calcareous shaleThese litho unit are overlain by limestone horizon. These units do not occur as well-defined stratum, and occurs in transition state with each other. At some places it occurs with limestone horizon as well. In some of the boreholes, limestone was encountered after this litho unit. The average thickness of this litho-unit is about 12m.- SandstoneThis unit is overlain by siliceous limestone/ calcareous shale horizon and does not occur as a continuous layer. This lithounit was encountered only in few boreholes. Sandstone occurs as weakly compacted rock with intercalations of silt and shale at places. The total thickness of this litho unit was not measured however about 10m. thick sandstone was penetrated by boreholes.
5. Fragmentation Modelling/Prediction
Quantifying size distribution of fragmented rock is very difficult and requires either direct method such as sieve analysis or indirectly by making model for the fragmented rock. Direct method of sieve analysis is time consuming and very laborious. Additionally, the blaster man can investigate the fragmented size and decide whether or not secondary blasting is needed. However, although the indirect method is accurate, it is not a perfect method for analyzing fragmented rock size. Indirect method is also classified in to two broad categories, which are empirical modeling and mechanical modeling. The empirical models assume that finer fragmentation is as a result of higher input energy from explosives (through higher powder factors). The mechanistic models, on the other hand, track the physics of detonation and energy transfer for specific blast designs (Bruno, 2016). The mechanistic models are not popular in practice because they are very sophisticated and require more input data (Johnson, 2014).
5.1. Kuz-Ram Model
The models for prediction of size distribution are generally classified into two categories: empirical and mechanistic models. Due to the sophisticated nature of the mechanistic models, empirical models are most commonly used in practice.The Kuz-Ram model is one of the best empirical modeling methods. Amongst all empirical modeling techniques mentioned before, Kuz-Ram model lies in its simplicity in terms of input data collection, and its direct linkage between blast design parameters and rock fragmentation (Cunningham, 2005). There are three basic and important equations in this model: Kusnetsov equation, Rosine-Rammler equation and the uniformity equation.I. Kuznetsov Equation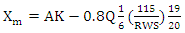 | (1) |
Where 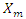 = mean particle size, cm; A = rock factor varying between 0.6 and 22, depending on hardness and structure]; K = powder factor, kg explosive per cubic meter of rock; Q = mass of explosive in the hole, kg; and RWS = Relative Weight Strength, 115 is indicates that RWS of TNT but if we use another explosive, we use particular value of the explosives.II. Rosin-Rammler equation
= mean particle size, cm; A = rock factor varying between 0.6 and 22, depending on hardness and structure]; K = powder factor, kg explosive per cubic meter of rock; Q = mass of explosive in the hole, kg; and RWS = Relative Weight Strength, 115 is indicates that RWS of TNT but if we use another explosive, we use particular value of the explosives.II. Rosin-Rammler equation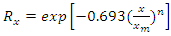 | (2) |
where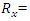 mass fraction retained on screen opening x; and n = uniformity index, usually between 0.6 and 2.2.III. Uniformity equation
mass fraction retained on screen opening x; and n = uniformity index, usually between 0.6 and 2.2.III. Uniformity equation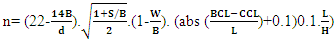 | (3) |
Where B = burden, m; S = spacing, m; d = hole diameter, mm; W = standard deviation of drilling precision, m; L = charge length, m; BCL = bottom charge length, m; CCL = column charge length, m; and H = bench height, m.
5.1.1. Rock Factor
Cunningham attempted to cure the insufficiency identified with the way that the rock factor doesn't reflect characteristics properties of the rock mass (1983). The equation proposed by Lilly identified with the blastability of the rock mass is given below and the variable utilized are given in Table 3.Table 3. Definition and calculation of the variables used in the determination of Rock Factor A (Lilly, 1986)
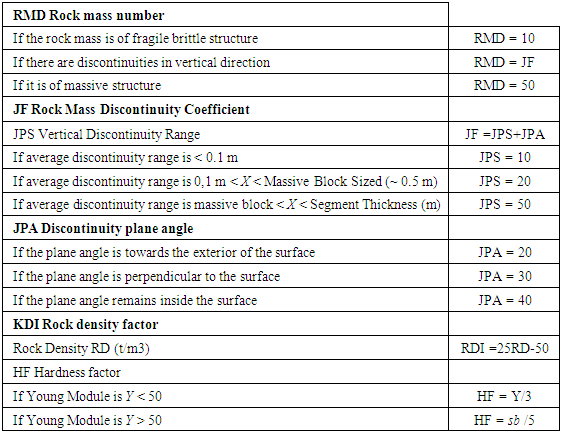 |
| |
|
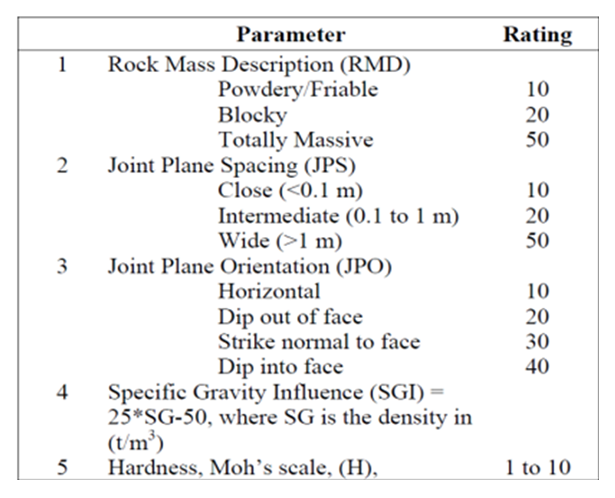 | Figure 1. Rock parameter description and rating (source: Lilly 1986) |
5.2. Modified Kuz-Ram Model
The Modified Kuz-Ram model is similar to the original Kuz-Ram model but the Kuznetsov equation is modified by an additional factor of 0.073 included in the formula for predicting the mean fragment size (Gheibie et al., 2009). The reason is joint aperture is considered as an effective parameter. The uniformity index of the Kuz-Ram model is also replaced by a modified uniformity index which is based on the original uniformity index equation proposed by Cunningham and a blastability index (BI). This model is a two-parameter fragmentation size distribution model that can easily be determined on the field. Its defects lie in the fact that it does not consider the effect of timing on fragmentation and has no upper limit for sizes. The Rossin Rammler equation (6) and Cunningham’s uniformity index equation (8) are maintained as in the original Kuz-Ram model. Equation (10) and Equation (12) below shows how the mean fragment size and blastability values are obtained (Gheibie et al., 2009).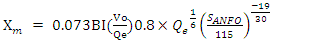 | (4) |
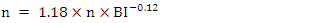 | (5) |
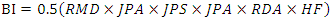 | (6) |
where, 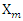 is the mean fragment size, cm; BI is the blastability index, Vo is the volume of rock broken by one blasthole, m3, Qe is the mass of explosive in each hole, kg; SANFO is the relative weight strength of the explosive to ANFO, n is the uniformity index, n` is the modified uniformity index and RMD, JPS, JPA, RDI and HF have the same meanings as defined in table, above.
is the mean fragment size, cm; BI is the blastability index, Vo is the volume of rock broken by one blasthole, m3, Qe is the mass of explosive in each hole, kg; SANFO is the relative weight strength of the explosive to ANFO, n is the uniformity index, n` is the modified uniformity index and RMD, JPS, JPA, RDI and HF have the same meanings as defined in table, above.
6. Data Collection
These data are collected from Derba Midroc Cement quarry site acquired through field measurement analysis and secondary data from files and documents. Six blasts from the mine are considered.
6.1. Geometric Blast Design Data
Six geometric blast design sample were taken from DMC and from the file and presented as follows in the below.Table 4. Blast Design Parameter
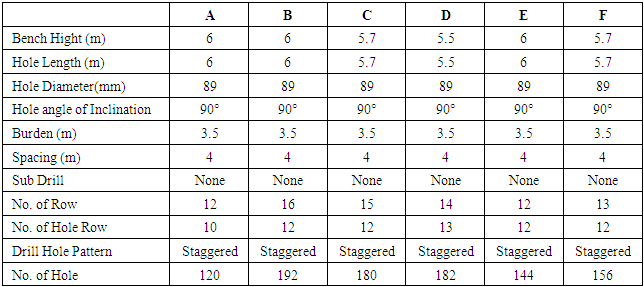 |
| |
|
6.2. Explosive Data
Table 5. Explosive Parameter
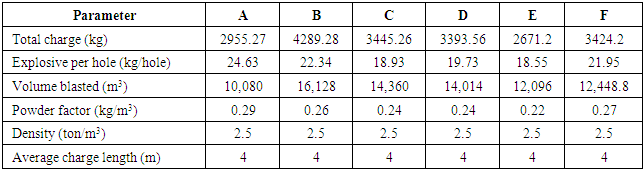 |
| |
|
6.3. Rock Parameter
The rock data at the lime stone quarry was obtained from the lime stone quarry at Derba and from the geology department. The information that we can get from the data included the Uniaxial Compressive strength, rock density, joint spacing, poison ratio and young’s modulus to determine the Rock mass description (RMD), Joint plane spacing (JPS), Joint plane angle (JPA), Rock density influence (RDI) and the Hardness Factor (HF) to build the predictive models. Table 6. Rock Data
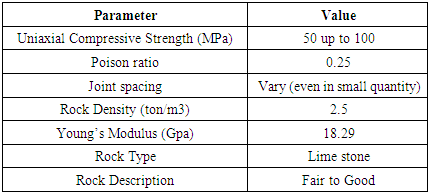 |
| |
|
7. Data Analysis
7.1. Fragmentation Prediction
After data collecting from Derba Midroc quarry like, the geometric, explosive and rock parameters were used for the prediction of fragmentation that used for analyzation process.We are using Kuz-Ram and Modified Kuz-Ram models, chosen due to the following reasons:• They are the best method of empirical analysis from the other.• The Modified Kuz-Ram model was introduced to remove some of the weaknesses of the Kuz-ram model.• The data required as input for these models are relatively easy to gather.A model (Figure 2) was developed in MS Excel 2016 for the prediction of the fragmentation size distribution.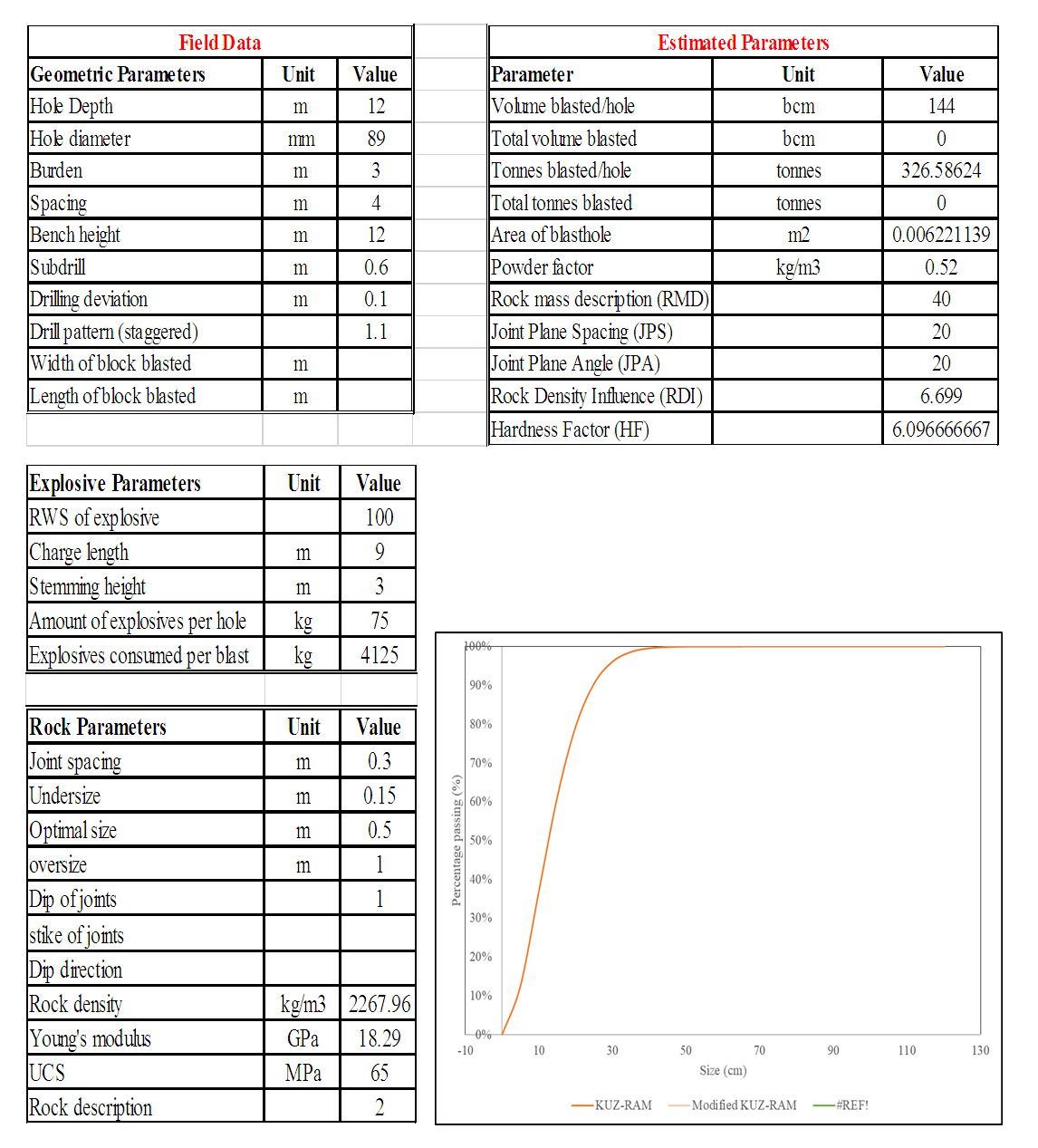 | Figure 2. Excel Model for Predictions |
8. Result and Discussion
8.1. Fragmentation Prediction
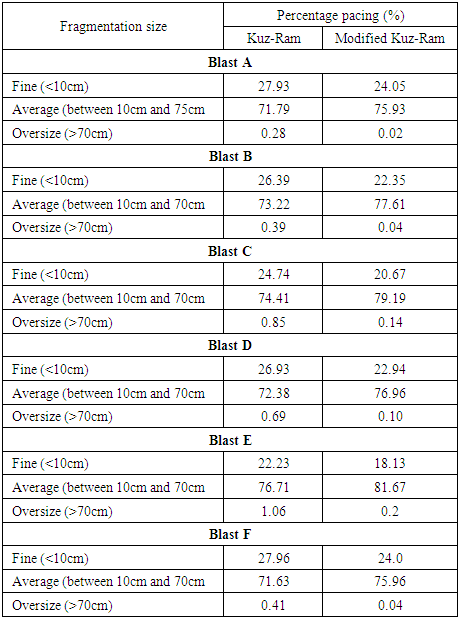
The results of the prediction of fragmentation for all blasts at Derba Midroc Cement limestone quarry by Kuz-Ram and Modified Kuz-Ram are shown in a table 7. The Summarization of the fragmentations are presented in comparison form between two methods, Kuz-Ram and Modified Kuz-Ram.Table 7. Fragmentation Prediction Summary from Blast A to Blast F
 |
| |
|
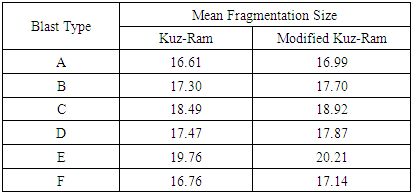
Fragments from blasting with size less than 10cm are considered as fines. The fines (<10cm) predicted by the Kuz-Ram and Modified Kuz-Ram models for all blasts are shown in Table 7. The fines (<10cm) predicted by the Kuz-Ram and Modified Kuz-Ram models for all blasts are not more than 27.96% and 24.05% respectively as shown in Table 7 above. This implies that both the models under predicted the number of fines produced. The fragmentation size which is very recommended from the blast (between 10cm and 70cm) was predicted for all blast as shown on the table above are not less than 71.63% by Kuz-Ram and 75.93% for Modified Kuz-Ram as presented in Table 7. The oversize above 70cm, that the company need another treatment like secondary blasting or hammering was predicted as follows. The oversize (>70cm) predictions for all blasts as shown in the table 7 above are not considerable and not more than 1.06% by Kuz Ram and 0.2% and by Modified Kuz-Ram models. Almost 98.94% of the fragmentation in which the Kuz-Ram fragmentation model result are predicted under oversize and no need of external or additional operation and it is directly goes to the primary crusher. And also, as we see in the Modified Kuz-Ram model around 99.80% were predicted under oversize material. This implies that almost the blasting practice in Derba Midroc limestone quarry site were very healthy.Mean fragment size The predicted mean fragment sizes for all Blast as shown in Table 8 below are between 16.61 and 19.76cm for the Kuz-Ram and for the Modified Kuz-Ram models between 16.99 and 20.21cm.Table 8. Summary of Predicted Mean Fragment Sizes for the Blasts
 |
| |
|
When we compare the two-fragmentation prediction model the Modified Kuz-Ram model is still near to the actual mean fragmentation size as compared to the company data that installed from the crusher unit.
9. Conclusions and Recommendations
9.1. Conclusions
v The desired size (between 10cm and 70cm) contain more percentage than others (under size and oversize).v Both Kuz-Ram and Modified Kuz-Ram model gave best prediction when related to the company prediction system that already installed in the crusher unit and displayed on the screen in control unit.v Modified Kuz-Ram is better for fragmentation prediction model compared to Kuz-Ram model in all blast type (from Blast A to Blast F).v In all prediction of fragmentations (from Blast A to Blast F) except in Blast E, above 99% of fragmentation did not need further treatment like secondary blasting or hammering after primary blasting is completed.v The average amount of fine produced in six blast is not more than 26.03% by Kuz-Ram and 22.02% by Modified Kuz-Ram method. And also, in both model the average oversize material produced is less than 1%. Therefore, the blasting practice of the company is very healthy.
9.2. Recommendations
§ The company must be attaching with the modified Kuz-Ram model for prediction of fragmentation at Midroc Derba limestone quarry in order to buildup best blasting practice with precise fragmentation.§ Since the results of the predictions from all the models had a strong correlation, they may be used in designing blasts for virgin areas with sufficient knowledge of the rock properties as this may be better than the trial-and-error methods commonly used in industry.
References
| [1] | Cunningham, C. V. B. (2005), “The Kuz-Ram Fragmentation Model – 20 Years On”, Brighton Conference Proceedings 2005, R. Holmberg et al. (ed), European Federation of Explosives Engineers, pp. 201-210. |
| [2] | Cunningham, C.V.B. (1983). The Kuz–Ram model for prediction of fragmentation from blasting. Proceedings of 1st International Symposium on Rock Fragmentation by Blasting, Lulea, pp 439–454. |
| [3] | Cunningham, C.V.B. (1987). Fragmentation estimations and the Kuz–Ram model – four years on. Proceedings of Second International Symposium on Rock Fragmentation by Blasting, Keystone, Colorado. pp 475–487. |
| [4] | Gadikor, J. (2018). Optimization of Drilling and Blasting Practices at a Western US Open Pit Copper Mine. Montana tech. |
| [5] | Gheibie, S., Aghababaei, H., Hoseinie, S. H. and Pourrahimian, Y. (2009), “Modified Kuz-Ram Fragmentation Model and its use at the Sungun Copper Mine”, International Journal of Rock Mechanics & Mining Sciences, Vol. 46, pp. 967 – 973. |
| [6] | Hustrulid, W. (1999) Blasting Principles for Open Pit Mining, Volume 1-General Design Concepts. A.A. Balkema, Rotterdam. |
| [7] | Johnson, C. E. (2014), “Fragmentation Analysis in the Dynamic Stress Wave Collision Regions in Bench Blasting”, Unpublished PhD Thesis Report, University of Kentucky, U.S.A, 158 pp. |
| [8] | Kanchibotla, S. S., Valery, W. and Morrell, S. (2001), “Modelling Fines in Blast Fragmentation and Its Impact on Crushing and Grinding”, Julius Kruttschnitt. |
| [9] | Kansake B. A. (2016), “Comparative Analysis of Rock Fragmentation Models: A Case Study”, Thesis Report, University of Mines and Technology (UMaT), Tarkwa. |
| [10] | Kazem O, Bahareh A. (2006). Prediction of Rock Fragmentation in Open Pit Mines, using Neural Network Analysis. 15th international symposium on mine planning and equipment selection, Turin, Italy. |
| [11] | Kuznetsov, V.M. (1973). The mean diameter of fragments formed by blasting rock. J Min Sci; 9: pp 144–148. |
| [12] | Lilly, P.A. (1986): “An Empirical Method of Assessing Rock Mass Blastability.” Proceedings of Large Open Pit Mining Conference, Davidson, J. R. (ed.), AUSIMM, Parkville, Victoria. pp. 89 – 92. Mineral Research Centre Internal Report, University of Queensland, Australia, 20 pp. |
| [13] | Ouchterlony, F. (2005). The Swebrec function: linking fragmentation by blasting and crushing. Mining Technology (Trans. Inst. Min. Metall. A), March 2005, Vol. 114, pp. 29-44. |
| [14] | Rosin R, Rammler E. Laws governing the fineness of coal. J Inst Fuels 1933; 7: 29–36. |
| [15] | Vamshidhar, K. and Venkatesh, H. S. (2010), “Review of Models for Prediction of Rock Fragmentation due to Blasting”, Journal of the Explosives Safety and Technology Society (Visfotak) India: Dealing with Safety and Technological Aspects of The Explosives Industry, Vol. 5, pp. 23 – 30. |


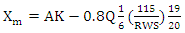
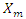 = mean particle size, cm; A = rock factor varying between 0.6 and 22, depending on hardness and structure]; K = powder factor, kg explosive per cubic meter of rock; Q = mass of explosive in the hole, kg; and RWS = Relative Weight Strength, 115 is indicates that RWS of TNT but if we use another explosive, we use particular value of the explosives.II. Rosin-Rammler equation
= mean particle size, cm; A = rock factor varying between 0.6 and 22, depending on hardness and structure]; K = powder factor, kg explosive per cubic meter of rock; Q = mass of explosive in the hole, kg; and RWS = Relative Weight Strength, 115 is indicates that RWS of TNT but if we use another explosive, we use particular value of the explosives.II. Rosin-Rammler equation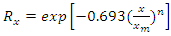
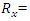 mass fraction retained on screen opening x; and n = uniformity index, usually between 0.6 and 2.2.III. Uniformity equation
mass fraction retained on screen opening x; and n = uniformity index, usually between 0.6 and 2.2.III. Uniformity equation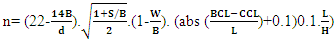

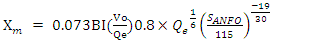
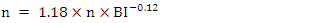
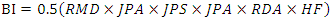
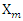 is the mean fragment size, cm; BI is the blastability index, Vo is the volume of rock broken by one blasthole, m3, Qe is the mass of explosive in each hole, kg; SANFO is the relative weight strength of the explosive to ANFO, n is the uniformity index, n` is the modified uniformity index and RMD, JPS, JPA, RDI and HF have the same meanings as defined in table, above.
is the mean fragment size, cm; BI is the blastability index, Vo is the volume of rock broken by one blasthole, m3, Qe is the mass of explosive in each hole, kg; SANFO is the relative weight strength of the explosive to ANFO, n is the uniformity index, n` is the modified uniformity index and RMD, JPS, JPA, RDI and HF have the same meanings as defined in table, above.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML






