M. N. Al-Maghrabi
Mining Engineering Department, King Abdulaziz University, Jeddah, Saudi Arabia
Correspondence to: M. N. Al-Maghrabi, Mining Engineering Department, King Abdulaziz University, Jeddah, Saudi Arabia.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Column flotation has been found to yield better performance than conventional flotation cells, particularly with fine particles. Three distinctive zones can be observed in a counter current flotation column: the Collection zone; the Interface zone; and the Froth zone. Mineral particles are collected and transported from the collection zone to the froth zone by air bubbles, where some of the collected particles are finally stabilized. However, during the process of collection and stabilization, some particles are dropped back because of sudden deceleration of bubbles in the Interface zone and bubble coalescence in the Froth zone. Consequently, these dropped back particles remain in movement along the three zones. In the present work the detachment of particles caused by bubbles coalescence in the froth zone have been considered as a portion of the total dropped back particles. This paper describes the process by which the transit probabilities of drop back particles can be determined with the help of recoveries of the zones. The Markov process has been used to determine the steady state probabilities of dropped back particles from the transit probabilities.
Keywords:
Column flotation, Drop back, Particles, Steady state, Transit probabilities
Cite this paper: M. N. Al-Maghrabi, Steady State Probabilities of Drop Back Particles in Column Flotation, International Journal of Mining Engineering and Mineral Processing , Vol. 3 No. 1, 2014, pp. 6-9. doi: 10.5923/j.mining.20140301.02.
1. Introduction
Column flotation can be operated in either of the following two modes: counter current mode or co-current mode [1]. The difference between the two modes is that, the dropped back particles from the froth in the co-current mode are no longer re-collected while in counter current mode the particles are available for re-collection. The present work deals with the later mode. Three zones can be observed in a counter current flotation column where air bubbles rise against the downward feed flowing slurry. These zones are collection zone (pulp zone), interface zone and froth zone (cleaning zone) as shown in Figure 1. Mineral particles are collected and transported from the collection zone to the froth zone as a result of attachment to air bubbles. Some of the collected particles are dropped back due to the effect of interface and froth zones. However, some researchers have pointed out that the drop back action does not occur within the froth zone [2].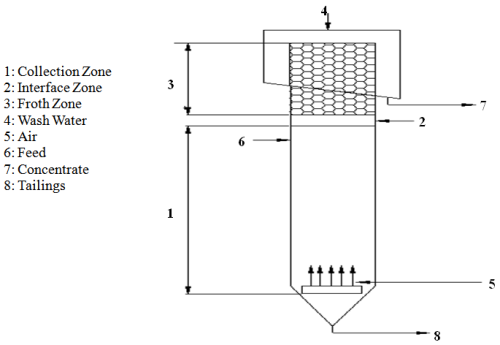 | Figure 1. Zones of Column flotation |
The effect of interface mainly involves the sudden deceleration of bubbles where it rises from the collection zone and hits the base of the froth. This phenomenon creates a mechanical shock on the particles that result in dropping back of the weakly attached particles. However, the effect of froth also involves the stability of the froth where the weakly floatable particles and gangue do not remain floatable because of bubble coalescence. A model to describe the froth recovery in terms of operating variables was reported [3]. It can also be expected that intelligent techniques may be incorporated to solve variety of problems in the near future [4]. Two zones situation of flotation column have been considered in an earlier study by Al-Maghrabi [5].In the present work the detachment of particles caused by bubbles coalescence in the froth zone have been considered as a portion of the total dropped back particles. The dropped back particles, however, remain in movement among the three zones of the column. The Markov process has been used to determine the steady state probabilities of dropped back particles from the transit probabilities.
2. Methodology
The types of particles considered inside the column are:1. The particles recovered in the concentrate2. The particles recovered in the tailings3. The particles moving among the zones of the column. In this study, the particles moving among the zones of the column are termed as dropped back particles. Let D is total dropped back particles and D1 is the portion of the dropped back particles due to the effect of interface zone and D2 is the portion of the dropped back particles due to the effect of the froth zone, thus D = D1 + D2The total dropped back particles can be measured by isolating the froth zone from the collection zone (Falutsu and Dobby; 1989). This kind of situation can be modeled by separate states describing the drop back particles moving among the zones of the column based on the principles of Markov process [6]. Let state 1 represents the situation in which the dropped back particles are in the collection zone, state 2 represents the situation in which the dropped back particles are in the interface zone and state 3 represents the situation in which the dropped back particles are in the froth zone. The entire process may be best visualized by employing a tree diagram as shown in Figure 2. This figure shows a probability tree in which upward branches represent a movement to state 1; downward branches show a movement to state 3; and the branches in between to state 2.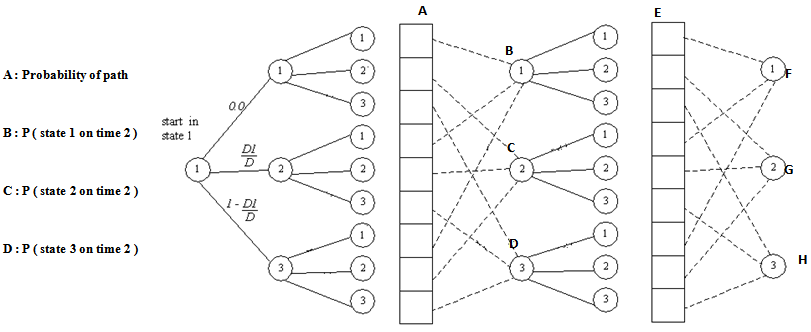 | Figure 2. Paths of dropped-back particles in column flotation |
3. Transition Probabilities
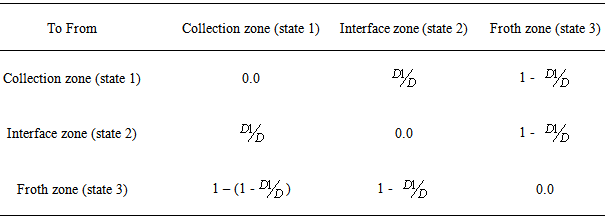
The author assumes that the particles which are dropped back during the collection zone are more likely to be the same particles dropped back due to the effect of the interface. Figure 2 depicts that if the dropped back particle is in particular state and remains in the same state during the succeeding times, then the transit probabilities is zero.If dropped back particle is in state 1, the probability that it will be in state 2 during the succeeding times is 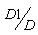 and the probability that it will be in state 3 during the succeeding times is 1 -
and the probability that it will be in state 3 during the succeeding times is 1 -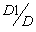 .If the dropped back particle is in state 2, the probability that it will be in state 1 during the succeeding times is
.If the dropped back particle is in state 2, the probability that it will be in state 1 during the succeeding times is 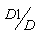 and the probability that it will be in state 3 during the succeeding times is 1 -
and the probability that it will be in state 3 during the succeeding times is 1 - 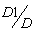 .If the dropped back particle is in state 3, the probability that it will be in state 2 during the succeeding times is 1 -
.If the dropped back particle is in state 3, the probability that it will be in state 2 during the succeeding times is 1 - 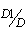 and the probability that it will be in state 1 during the succeeding times is 1 – (1 -
and the probability that it will be in state 1 during the succeeding times is 1 – (1 - 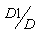 ). These transition probabilities of dropped back particles are shown in Table 1.
). These transition probabilities of dropped back particles are shown in Table 1.Table 1. Transition probabilities of dropped back particles in column flotation
 |
| |
|
4. Mathematical Formulation
Referring Figure 2, the following results can be drawn: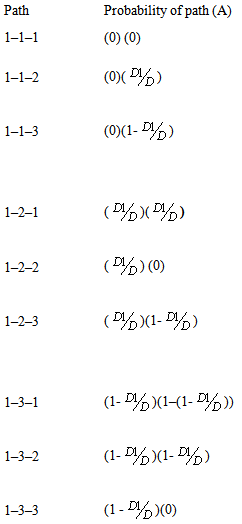 B = P (state 1 on time 2) = probability that the drop back particles will be in state 1 at the end of time 2 (given that it was in state 1 at time 0) = path 1–1–1 + path 1–2–1 + path 1–3–1 =
B = P (state 1 on time 2) = probability that the drop back particles will be in state 1 at the end of time 2 (given that it was in state 1 at time 0) = path 1–1–1 + path 1–2–1 + path 1–3–1 = 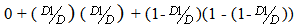 C = P (state 2 on time 2) = path1-1-2 + path 1-2-2 + path 1-3-2 =
C = P (state 2 on time 2) = path1-1-2 + path 1-2-2 + path 1-3-2 = 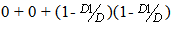 D = P (state 3 on time 2) = path 1-1-3 + path 1-2-3 + path 1-3-3 =
D = P (state 3 on time 2) = path 1-1-3 + path 1-2-3 + path 1-3-3 = 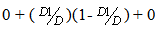 Similarly at time 3, the probability will be
Similarly at time 3, the probability will be 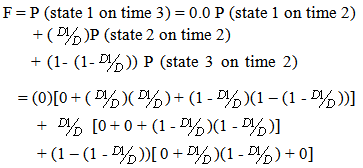 | (1) |
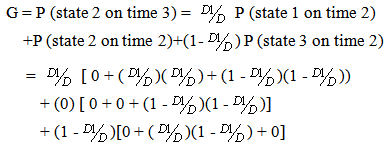 | (2) |
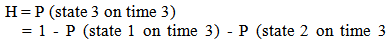 | (3) |
Regarding the pattern of equations (1-3), it is possible to calculate the probability of the dropped back particles being in any state at any future time (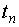 ). Therefore the following equations relating the “state probabilities” can be written as:
). Therefore the following equations relating the “state probabilities” can be written as: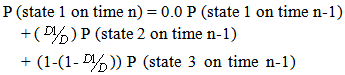 | (4) |
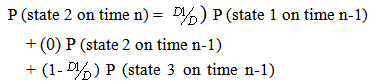 | (5) |
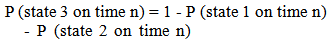 | (6) |
It is assumed that, the probability of the dropped back particles being in the existing state and previous state are the same when "n" is a very large number.P (state 1 on time n) = P (state 1 on time n-1) = P1P (state 2 on time n) = P (state 2 on time n-1) = P2Substituting equation (6) into equation (4) and (5) the State Probabilities can be obtained as under,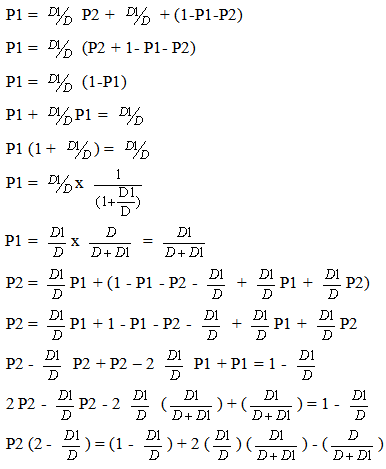 | (7) |
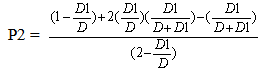 | (8) |
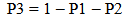 | (9) |
The above equations (7-9) represent the state probabilities.
5. Conclusions
A study has been made for counter current flotation column where collision of mineral particles with air bubbles followed by attachment that occurs in the collection zone. It has been observed that the particles are transported to the froth zone by air bubbles where some of the collected particles are finally stabilized. Further, it has been shown that during the process of collection and stabilization some particles are dropped back because of the effect of interface zone and froth zone. It has been observed that these dropped back particles, however, remains in movement along the three zones of the column. In the present work, an attempt has been made to describe the process by which the transit probabilities of the drop back particles are determined. Markov process has been used to determine the steady state probabilities of the dropped back particles from the transit probabilities.
References
| [1] | Contini, N. J., Wilson, S. W. and Dobby, G. S., Measurement of rate data in flotation column. In: K.V.S. Sastry (Editor), Column Flotation’ 88, 1988, 81-89. |
| [2] | Falutsu, M. and Dobby, G.S., Direct measurement of froth drop back and collection zone recovery in a laboratory flotation column. Mineral Engineering, 1989, 2, 337-386. |
| [3] | Yianatos, J. B. , Bergh, L. G. and corte’s, G.A. Froth zone modelling of an industrial flotation column. Mineral Engineering, 1998, 11, 423-435. |
| [4] | Bergh, L. G. and Yianatos, J. B., Flotation column automation: state of the art Control Engineering Practice, 2003, 11, 67-72. |
| [5] | Al-Maghrabi, M. N. A probabilistic approach to column flotation. The European Journal of Mineral Processing and Environmental Protection, 2004, 4, pp 91-94. |
| [6] | Ullmann. J.E., Fundamental of probability. In: theory and problems of Quantative Methods in Management, 1976, Schaum’s outline series, 97-99. |



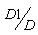 and the probability that it will be in state 3 during the succeeding times is 1 -
and the probability that it will be in state 3 during the succeeding times is 1 -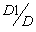 .If the dropped back particle is in state 2, the probability that it will be in state 1 during the succeeding times is
.If the dropped back particle is in state 2, the probability that it will be in state 1 during the succeeding times is 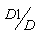 and the probability that it will be in state 3 during the succeeding times is 1 -
and the probability that it will be in state 3 during the succeeding times is 1 - 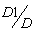 .If the dropped back particle is in state 3, the probability that it will be in state 2 during the succeeding times is 1 -
.If the dropped back particle is in state 3, the probability that it will be in state 2 during the succeeding times is 1 - 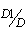 and the probability that it will be in state 1 during the succeeding times is 1 – (1 -
and the probability that it will be in state 1 during the succeeding times is 1 – (1 - 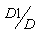 ). These transition probabilities of dropped back particles are shown in Table 1.
). These transition probabilities of dropped back particles are shown in Table 1.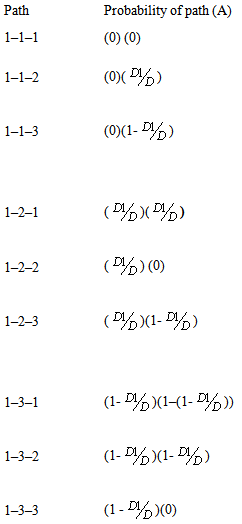 B = P (state 1 on time 2) = probability that the drop back particles will be in state 1 at the end of time 2 (given that it was in state 1 at time 0) = path 1–1–1 + path 1–2–1 + path 1–3–1 =
B = P (state 1 on time 2) = probability that the drop back particles will be in state 1 at the end of time 2 (given that it was in state 1 at time 0) = path 1–1–1 + path 1–2–1 + path 1–3–1 = 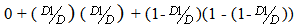 C = P (state 2 on time 2) = path1-1-2 + path 1-2-2 + path 1-3-2 =
C = P (state 2 on time 2) = path1-1-2 + path 1-2-2 + path 1-3-2 = 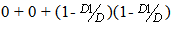 D = P (state 3 on time 2) = path 1-1-3 + path 1-2-3 + path 1-3-3 =
D = P (state 3 on time 2) = path 1-1-3 + path 1-2-3 + path 1-3-3 = 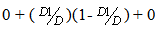 Similarly at time 3, the probability will be
Similarly at time 3, the probability will be 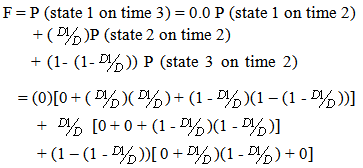
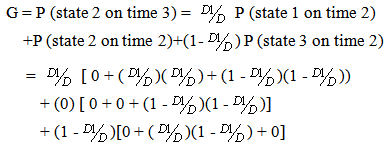
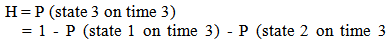
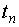 ). Therefore the following equations relating the “state probabilities” can be written as:
). Therefore the following equations relating the “state probabilities” can be written as: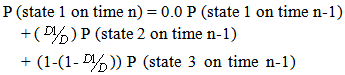
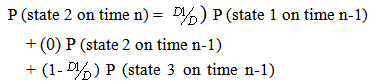
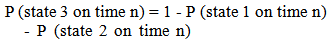
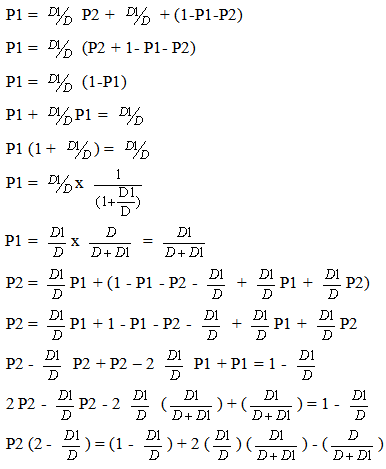
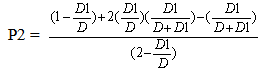
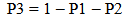
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML