Karmous Mohamed Salah
Physics Department, Faculty of Sciences of Sfax. Road Soukra km 4, B.P. n° 802-3038. Sfax. Tunisia
Correspondence to: Karmous Mohamed Salah , Physics Department, Faculty of Sciences of Sfax. Road Soukra km 4, B.P. n° 802-3038. Sfax. Tunisia.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
A study of structural and mechanical properties of Nacrite using Molecular Dynamics Simulations based on energy minimization technique was investigated. Several mechanical properties have been calculated, such as the full elastic constants tensors, shear modulus, bulk modulus, Young modulus along a, b and c directions. The S- and P-wave velocities as well as Poisson ratio were also evaluated. The obtained elastic constant shows that C11≈C22 and higher than C33, indicating that Nacrite is more flexible in a and b direction than c one. The predicted bulk and shear modulus are respectively equal to 56.41 and 20.28 GPa. The Poisson’s ratios exhibit prominent anisotropy, with values ranging from 0.03 to 0.53. The Young’s modulus in the [100] and [010] directions (E1 and E2) is larger than E3 (Young moduli in[001] direction). In this study Vp=17.59 Km/s, Vs=8.68 Km/s and giving Vp/Vs ratio equal to 2.02. All these results reveal that Nacrite is less compressible than the other clays (kaolinite). All calculations were performed using GULP program.
Keywords:
Prediction, Nacrite, Elastic, Molecular Dynamics Simulation, GULP
Cite this paper:
Karmous Mohamed Salah , "Elastic Constant Prediction of Nacrite: Molecular Dynamics Simulations", International Journal of Mining Engineering and Mineral Processing , Vol. 1 No. 3, 2012, pp. 115-119. doi: 10.5923/j.mining.20120103.03.
1. Introduction
Clay minerals are the most abundant materials in sedimentary basin. The most common like kaolinite is found in various mudstones[1]. Kaolin minerals are dioctahedral clays of 1:1 layer type with chemical composition Al2Si2O5(OH)4. Kaolinite, Dickite, and Nacrite are polytypes.Nacrite is the rarest of the kaolin polymorph, it is characterized by Al4Si4O18H8 structural formula, monoclinic structure of space group of Cc , a= 8.906(2), b = 5.146(1), c = 15.664(3)Å,β= 113.58(3)° and V = 657.9(3) Å3[2]. The basic structural element of kaolin minerals consists in a tetrahedral[SiO4] and an octahedral[AlO2(OH)4] sheet linked together by a common plane of oxygens and hydroxyls (figure 1). Only 2/3 octahedral sites are occupied by Al3+, the remaining 1/3 being vacant[3]. Nacrite is structurally distinct from other members of kaolin group, being the most closely stacked in the c-axis direction.However, elastic properties of clay minerals are almost unknown[4, 5] and there is few available experimental data. This is mainly due to the difficulty presented by their intrinsic properties. The small grain size makes it difficult to isolate an individual crystal of clay large enough to measure acoustic properties[6, 7].Despite their importance, the single-crystal elastic moduliof clay minerals have not been measured experimentally, because of technical difficulties associated with the small grain size. There is also considerable uncertainty in atomic force microscopy[6].Recently, several group attempts to predict, theoretically, elastic constant and mechanical properties of kaolin family; For kaolinite, values from first-principles calculations exist for the ideal structure[8, 9], or from molecular dynamics simulation[4, 10]. For Nacrite, only a first principle calculations exists[11] to predict elastic behaviour.In this work, a prediction of elastic constant, shear modulus, bulk modulus, Young modulus along a, b and c directions, the S- and P-wave velocities as well as Poisson ratio were also evaluated using molecular dynamics simulation based on GULP program.
2. Materials and Methods
2.1. Simulation Principle
The structural and mechanical properties of Nacrite were simulated using GULP program[12].The GULP program offers added advantage that it permits the inclusion of atom polarisability through the use of the core-shell model[13].The potential model describing the effective forces acting between the atoms in the structure has the following components[14]:*A two-body short-range term describes repulsions from electron cloud overlap and attractions due to dispersion and covalence. In this study we describe cation-O and the O-O interactions using a Buckingham function: 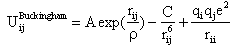 , where the exponential term describes the repulsive energy and the r6 term the longer range attraction (table 1). *A three-body short-range term describes angular dependent covalent forces. A simple approach is to include bond-bending terms about the tetrahedral cation of the type: Uthb = 1/2Kthb(θ − θ0)2. where Kthb is the harmonic three-body force constant, and θ and θ0 are the observed and ideal tetrahedral O-T-O bond angles, respectively (table 1).
, where the exponential term describes the repulsive energy and the r6 term the longer range attraction (table 1). *A three-body short-range term describes angular dependent covalent forces. A simple approach is to include bond-bending terms about the tetrahedral cation of the type: Uthb = 1/2Kthb(θ − θ0)2. where Kthb is the harmonic three-body force constant, and θ and θ0 are the observed and ideal tetrahedral O-T-O bond angles, respectively (table 1).| Table 1. Potential used in simulation |
| | Two body short range interactiona | | Atom 1 | Atom 2 | Potential | A/eV | ρ/Å | C/eVÅ6 | | Al1 c | O1 s | Buckingham | 1460 | 0.299 | 0.00 | | O2 c | Al1 c | Buckingham | 1140 | 0.299 | 0.00 | | Si1 c | O1 s | Buckingham | 1280 | 0.321 | 10.7 | | O2 c | Si1 c | Buckingham | 984 | 0.321 | 10.7 | | O1 s | O1 s | Buckingham | 22800 | 0.149 | 27.9 | | O2 c | O1 s | Buckingham | 22800 | 0.149 | 27.9 | | O2 c | O2 c | Buckingham | 22800 | 0.149 | 27.9 | | H1 c | O1 s | Buckingham | 312 | 0.250 | 0.00 | | Morse potential | | Atom 1 | Atom 2 | Potential | De/eV | β/Å−1 | re/Å | | H1 c | O2 c | Morse-Coulomb | 7.05 | 2.20 | 0.949 | | Shell model interaction | | Atom 1 | Atom 2 | Potential | Ks/eVÅ−2 | | O1 c | O1 s | Spring | 74.90 | | Three body interaction | | Atom 1 | Atom 2 | Atom3 | Kthb/eV rad−2 | θ/° | | Si1 c | O1 s | O1 s | 2.097 | 109.470 | | Al1 c | O2 c | O1 s | 2.097 | 109.470 |
|
|
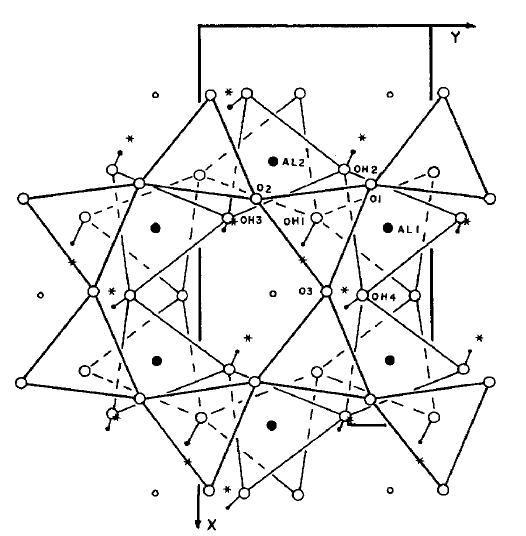 | Figure 1. Projection onto (001) of basal oxygens in the tetrahedral sheet of the second layer onto the octahedral sheet of the first layer. Small solid circles are H+ positions found in this study. Small open circles are centers of the vacant octahedral[17] |
* A term to describe electronic polarizability is required if dielectric and dynamic properties are to be modelled accurately. In this study the shell model was used, which provides a simple mechanical model of electronic polarizability. The core-shell self energy is given by Us = 1/2Ksr2 where Ks is the harmonic spring constant and r is the core-shell separation (Table 1).In this study, the libraries of potential used were the Catlow 1992[15]. The minimum energy configurations were derived by minimizing the potential energy as a function of the atomic coordinates and unit cell parameters.
3. Results and Discussion
3.1. Structural Simulation
The Nacrite structure used in the present work is initially based on crystallographic data[2] (figure 1), which gives, after optimization, a unit cell of C1 symmetry with lattice parameters a = 5.233 A˚ , b = 5.14 A˚ , c = 15.664 A˚ , and angles: α= 11.0933°, β= 111.0933°, γ = 59.2107° (table 2). The computed energy is equal to -848.784 eV.| Table 2. Bibliographic and simulated unit cell |
| | Nacrite CGA[11] | Nacrite LDA[11] | Nacrite[17] | This Work | | ρ (g/cm3) | 2.494 | 2.607 | - | 2.68 | | a (Å) | 9.020 | 8.910 | 8.906 | 5.233 | | b (Å) | 5.221 | 5.165 | 5.146 | 5.14 | | c (Å) | 14.881 | 14.571 | 15.664 | 15.6640 | | α (°) | 90 | 90 | 90 | 111.0933 | | β (°) | 101.11 | 101.24 | 113.58 | 111.0933 | | γ (°) | 90 | 90 | 90 | 59.2107 |
|
|
| Table 3. Simulated atomic coordinates of Nacrite |
| | Atom | x/a | y/b | z/c | | Al1 | -0.164600 | 0.475000 | 0.217700 | | Al1 | 0.165600 | 0.814600 | 0.217300 | | Si1 | -0.268800 | 0.671200 | 0.027700 | | Si1 | -0.611600 | 1.354600 | 0.027000 | | O1 | -0.508800 | 0.991000 | -0.004100 | | O1 | 0.025300 | 0.519300 | -0.018800 | | O1 | -0.438800 | 0.444600 | -0.019300 | | O1 | -0.168900 | 0.708100 | 0.138500 | | O1 | 0.450800 | 0.472800 | 0.138500 | | O2 | 0.067700 | 0.091300 | 0.143200 | | O2 | -0.076200 | 1.192200 | 0.283800 | | O2 | -0.451600 | 0.807600 | 0.283800 | | O2 | 0.162700 | 0.575900 | 0.282600 | | OH1 | -0.508800 | 0.991000 | -0.004100 | | OH1 | 0.025300 | 0.519300 | -0.018800 | | OH1 | -0.438800 | 0.444600 | -0.019300 | | OH1 | -0.168900 | 0.708100 | 0.138500 | | OH1 | 0.450800 | 0.472800 | 0.138100 | | H1 | 0.183600 | 1.085600 | 0.127700 | | H1 | 0.080140 | 1.014860 | 0.327900 | | H1 | -0.366400 | 0.852800 | 0.322800 | | H1 | 0.293100 | 0.570300 | 0.322800 |
|
|
Table 3 shows the structure, cell parameter, and unique atomic coordinates of the simulated structure determined using GULP program. In fact, in Nacrite, only one of the basal oxygens is located so it can pair up ideally with a directed hydrogen bond of this type. The other two basal oxygens (01 and 02) are located so that the actual bonds must be nearly at right angles to the ideal directed bonds, and this must affect the nacrite stability adversely[2].
3.2. Mechanical Properties
3.2.1. Elastic Constant
The elastic constant represent the second derivatives of the energy density with respect to strain: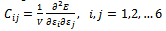 | (1) |
where Cij is a component of the stiffness matrix, C, E is the energy expression, V is the volume of the unit cell, and εi and εj are strain components.There by describing the mechanical hardness of the material with respect to deformation. Since there are 6 possible strains within the notation scheme employed here, the elastic constant tensor is a 6 x 6 symmetric matrix. The 21 potentially independent matrix elements are usually reduced considerably by symmetry.In table 4, elastic constant tensor is presented as well as previous results. The obtained elastic constant shows that C11≈C22 and higher than C33, indicating that Nacrite is more flexible in a and b direction than c one. These results present some different values from bibliographic data. Differences in elastic constants between various structures may, be partially due to difference in orientation of hydroxyl group[11]. Contrary to kaolinite which present more flexibility along a direction than b one[10].| Table 4. Elastic constant of Nacrite |
| | Nacrite CGA | Nacrite LDA | This work | | C11 | 147.6 | 131.8 | 215.24 | | C22 | 160.8 | 157.9 | 215.64 | | C33 | 64.8 | 75 | 67.92 | | C44 | 7.8 | 13.2 | 17.09 | | C55 | 8.8 | 17.7 | 10.92 | | C66 | 62.4 | 62.2 | 47.26 | | C12 | 45.4 | 41.5 | 117.14 | | C13 | 5.7 | 10.2 | 18.33 | | C14 | 0 | 0.6 | 0.42 | | C15 | 4.4 | -16 | 1.54 | | C16 | 0 | 0.1 | -1.7 | | C23 | 12 | 14 | 24.57 | | C24 | 0 | 0.4 | 1.93 | | C25 | 2.8 | -3.8 | 2.53 | | C26 | 0 | 0.1 | 1.45 | | C34 | 0 | 0.5 | -0.26 | | C35 | 0.2 | 9.3 | -0.46 | | C36 | 0 | 0.1 | -5.41 | | C45 | 0 | -0.5 | -5.34 | | C46 | 0.6 | -9.4 | -0.49 | | C56 | 0 | -0.1 | -1.32 |
|
|
3.2.2. Bulk and Shear Moduli
Like the elastic constant tensor, the bulk (K) and shear (G) moduli contain information regarding the hardness of a material with respect to various types of deformation. The bulk modulus is much more facile to determine experimentally than the elastic constant tensor. If the structure of a material is studied as a function of applied isotropic pressure, then a plot of pressure versus volume can be fitted to an equation of state where the bulk modulus is one of the curve parameters. Typically, a third- or fourth-order Birch-Murnaghan equation of state is utilized. Alternatively, the bulk and shear moduli are also clearly related to the elements of the elastic constant. In this study, predicted bulk equal to 56.41 GPa. Experimentally, bulk modulus values for kaolinite have been found between 21 and 55 GPa[15]. The theoretical models based on measured quantities on other sheet silicates[6] for the bulk modulus give a value of 55.5 GPa.Calculated shear modulus gives a 20.28 GPa value, it is comparable to the one reported in literature using molecular dynamics simulation[10].
3.2.3. Poisson’s Ratios
When materials are compressed along a particular axis they are most commonly observed to expand in directions orthogonal to the applied load. The property that characterizes this behavior is the Poisson’s ratio, which is defined as the ratio between the negative transverse and longitudinal strains. The majority of materials are characterized by a positive Poisson’s ratio (ν)[16].The poison’s ratios νij in the Oxi-Oxj planes (i,j=1,2,3) for loading in the Oxi direction are then given by: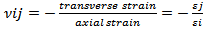 | (2) |
Table 5 shows the calculated Poisson’s ratios values of Nacrite. The Poisson’s ratios exhibit prominent anisotropy, with values ranging from 0.03 to 0.53.| Table 5. Young moduli and Poisson’s ratio of Nacrite |
| | Stress axis | x | y | z | | Young moduli (GPa) | 151.11037 | 147.53536 | 64.17514 | | Poissons Ratio (x) | | 0.52302 | 0.03067 | | Poissons Ratio (y) | 0.53569 | | 0.10011 | | Poissons Ratio (z) | 0.07221 | 0.23015 | |
|
|
3.2.4. Young’s and Shear Mouduli
The young’s moduli Ei for loading in the Oxi (i=1,2,3) directions are given by: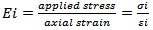 | (3) |
The applicability of this definition gives E1=151.11 GPa, E2=147.53 GPa and E3=64.17 GPa. Those value are lower compared with those found for Kaolinite (E1=187.22 GPa, E2=192.57 GPa and E3=49.53 GPa). The elasticity of Nacrite is highly anisotropic; the Young’s modulus in the[100] and[010] directions (E1 and E2) is larger than E3 (Young moduli in[001] direction). It is notable that Nacrite is less compressible compared to kaolinite.
3.2.5. Acoustic Velocities
Acoustic velocities are key quantities in the interpretation of seismic data. The polycrystalline averages of these acoustic velocities in a solid can be derived from the bulk and shear moduli of the material, as well as the density, ρ. There are two values, that for a transverse wave, Vs and that for a longitudinal wave, Vp, which are given by the following equations: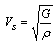 | (4) |
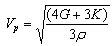 | (5) |
In this study Vp=17.59 Km/s, Vs=8.68 Km/s and giving Vp/Vs ratio equal to 2.02; this ratios is relatively high by comparing to those found for kaolinite 1.82[17].
4. Conclusions
This paper reports on prediction of elastic constant of Nacrite. The complete Cij elastic moduli were determined using molecular dynamics simulation. The elasticity of Nacrite is highly anisotropic. The calculated elastic constant tensor along c is much lower than the constants calculated along a and b. Nacrite deviates slightly by exhibiting a softer response, smaller elastic constants, which is a result of the weaker interlayer hydrogen bonding.
References
| [1] | N. H. Mondol, J. Jahren, Bjo̸rlykke K and I. Brevik, 2008. Elastic properties of clay minerals Experimental compaction of clays: relationship between permeability and petrophysical properties in mudstones. Led. Edge. 27,758-770. |
| [2] | H. Zheng and S.W. Bailey, 1994. Refinement of the nacrite structure Clays. Clay. Miner. 52, 42- 46. |
| [3] | A. Ben Haj Amara, J. Ben Brahim, A. Plançon and H. Ben Rhaiem, 1998. Étude par Diffraction X des Modes d'Empilement de la Nacrite Hydratée et Deshydratée . J. Appl. Cryst. 31, 654-662. |
| [4] | M. S. Karmous, 2011. Theoretical Study of Kaolinite Structure; Energy Minimization and Crystal Properties. W. J.Nano. Sci. Eng. 1, 62-66. |
| [5] | M. S. Karmous, 2012. A theroretical study of zeolite ABW; its mechanical and auxetic properties. Iran. J. Mater. Sci. Eng.9, 30-35. |
| [6] | M. Prasad, M. Kopycinska, U. Rabe, and W. Arnold, 2002. Measurement of Young's Modulus of Clay Minerals Using Atomic Force Acoustic Microscopy. Geophys. Res. Lett. 29, 13–16. |
| [7] | T. Vanorio, M. Prasad and A. Nur, 2003. Elastic properties of dry clay mineral aggregates, suspensions and sandstones. Nur, Geophys. J. Int. 155, 319–326. |
| [8] | H. Sato, K. Ono, C. T. Johnston and A. Yamagishi, 2005. First-Principles Studies on Elastic Constants of a 1:1 Layered Kaolinite Mineral,” Amer. Mineral. 90, 1824-1826. |
| [9] | P. H. J. Mercier and Y. Le Page,2008. Kaolin Polytypes Revi-sited Abinitio,” Acta. Crystallographica. 64, 131-143. |
| [10] | B. K. Benazzouz and A. Zaoui A, 2012. A nanoscale simulation study of the elastic behaviour in kaolinite clay under pressure. Mater. Chem. Phys. 132, 880-888. |
| [11] | B. Militzer, H.-R. Wenk, S. Stackhouse and L. Stixrude, 2011. First-Principles Calculation of the Elastic Moduli of Sheet Silicates and Their Application to Shale Anisotro-py. Amer. Mineral. 96, 125- 137. |
| [12] | J. D. Gale, 1997. GULP: A Computer Program for the Sym-metry-Adapted Simulation of Solids,” J. Chem. Society - Faraday Transactions. 93, 629-637. |
| [13] | J. N. Grima , R. Gatt , A. Alderson and K. E. Evans, 2005. On the origin of auxetic behaviour in the silicate α-cristobalite. Affiliation Information Department of Engineering,University of Exeter, North Park Road, Exeter, UK J. Mater. Chem. 15, 4003-4005 |
| [14] | D. R. Collins and C. R. A Catlow,1992. Computer Simulation of Structures and Cohesive Properties of Micas, Amer. Mineral. 77, 1172- 1181. |
| [15] | K. P. Schroder, J. Sauer, M. Leslie , C. R. A. Catlow and J. M. Thomas, 1992. Potential Functions for Silica and Zeolite Catalysts Based on ab Initio Calculations. 3. A Shell Model Ion Pair Potential for Silica and Aluminosilicates. Chem. Phys. Lett. 188, 320-325. |
| [16] | J. J. Williams, K. E. Evans and R. I. Walton, 2006. On the elastic constants of the zeolite chlorosodalite 2006 Appl. Phys.Lett. 88, 021914 -021916 |
| [17] | Z. Wang, H. Wang and M. E. Cates, 2001 Effective Elastic Properties of Solid Clays. Geophysics. 66, 428-440 |

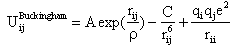 , where the exponential term describes the repulsive energy and the r6 term the longer range attraction (table 1). *A three-body short-range term describes angular dependent covalent forces. A simple approach is to include bond-bending terms about the tetrahedral cation of the type: Uthb = 1/2Kthb(θ − θ0)2. where Kthb is the harmonic three-body force constant, and θ and θ0 are the observed and ideal tetrahedral O-T-O bond angles, respectively (table 1).
, where the exponential term describes the repulsive energy and the r6 term the longer range attraction (table 1). *A three-body short-range term describes angular dependent covalent forces. A simple approach is to include bond-bending terms about the tetrahedral cation of the type: Uthb = 1/2Kthb(θ − θ0)2. where Kthb is the harmonic three-body force constant, and θ and θ0 are the observed and ideal tetrahedral O-T-O bond angles, respectively (table 1).
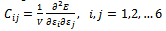
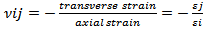
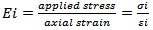
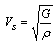
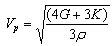
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML