M. R. Pinheiro
PO Box 12396 A'Beckett St Melbourne VIC AU 8006
Correspondence to: M. R. Pinheiro , PO Box 12396 A'Beckett St Melbourne VIC AU 8006.
| Email: |  |
Copyright © 2023 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
In this paper we present the complete tables resulting from the mathematical analysis of The Monty Hall Problem and discuss a solution presented by a professor who got a PhD from the Aarhus University. The results are that there is a flaw in the reasoning used by the professor and the Monty Hall Problem has been associated with a lot of mistaken mathematical analysis: Switching and sticking, the final choice in the game that generates the problem, return the same probability in what regards winning or losing. When the game became a mathematical problem, 10,000 readers expressed their certainty that this was the case.
Keywords:
Monty hall, Puzzle, Problem, Probability, Combinatorics
Cite this paper: M. R. Pinheiro , The Monty Hall Problem: Equal Probability, Modern International Journal of Pure and Applied Mathematics, Vol. 5 No. 1, 2023, pp. 1-3. doi: 10.5923/j.mijpam.20230501.01.
1. Introduction
The Monty Hall Problem is ([1])“connected to a TV show where a car would be hidden behind a door. The other doors would have something else behind them. The person participating in the game would choose one of the three doors and if they guessed right, like if they chose the door that had the car behind it, they would get the car. The presenter would open one of the two doors that remained (not chosen) after the person made the first choice. That door would never have the car.It is then said that they have studied the problem from the TV show and if the person changed their choice at that stage, like after the revelation of the contents of one of the two remaining doors, then the person would have more chances of getting the car because it was by studying the history of the show that they reached that conclusion, like, statistically, that would be the case.”Marilyn vos Savant, author of a Sunday Parade column, in 1991, is well known for having defended this theory [2]. She then said that if the person sticks they have 1/3 of chance of winning but if they switch they have 2/3 of chance instead [2]. The following diagram is presented as explanation for this theory by professors who studied at the Aarhus University1: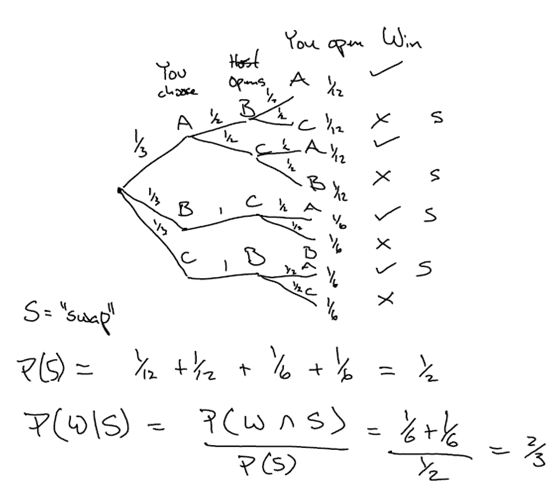 | Diagram 1 |
In this paper we present the table of possible choices and explain why this diagram is not OK.
2. Development
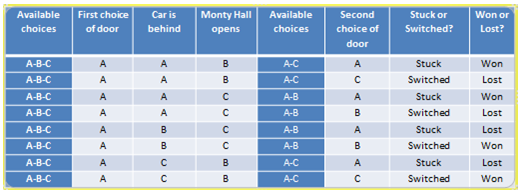
Call the doors A, B and C. The following table, which we shall call Table 1, describes the choices available if the first choice of door is A ([3]):Table 1
 |
| |
|
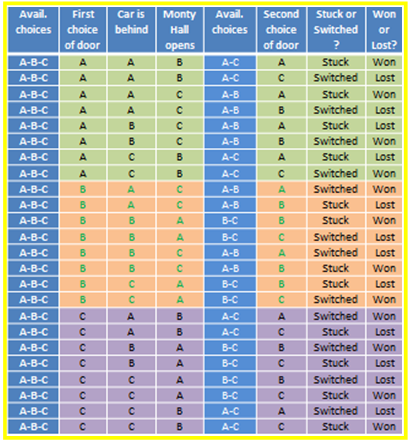
So, on the first four lines of the table, we have: if the first choice of door is A and the car is behind A Monty Hall could open B or C. A cannot be opened because it was the choice of the audience member and that one will remain closed until the last stage of the game, when the audience member is given the choice of sticking (keeping their choice as A) or switching (changing their choice of door to the remaining door). If the first choice of door is A, the car is behind A and Monty Hall opens door B (he can only open B or C), the audience member is left with two possibilities on the last stage of the game: A or C. If the choice is A, we have completed the line like this: A, A, B, A, stuck, won. To finish counting the options when we have A, A, B, it is missing choosing C in the end, so that the complete second line is A, A, B, C, switched, lost. Now all options with A, A, B in the beginning of the line have been explored, so let’s change to Monty Hall opens C, the other possibility if we have A, A in the beginning of the line. A, A, C means A and B as possible choices in the end of the game, so that we have two more lines: A, A, C, A and A, A, C, B. If the second choice of door is A and the first choice of door is A, the audience member stuck and won. If the second choice of door is B and the first choice of door is A, the audience member switched and lost, so that we have completed two more lines of the table: A, A, C, A, stuck, won and A, A, C, B, switched, lost. Now all options with A, A in the beginning of the line have been explored, so that we must hide the car behind B, following alphabetical order. First choice of door being A, car hidden behind B, Monty Hall has to open C, no other option. When he opens C, two doors will remain closed, A and B. The audience member may choose A or B, so that we have two more lines: A, B, C, A, stuck, lost (now car is behind B) and A, B, C, B, switched, won. We have now exhausted the options with beginnings A, A and A, B. Missing beginning with A, C. Now the door to be opened has to be B, no other option, and the two final lines are A, C, B, A, stuck, lost and A, C, B, C, switched, won. Probability: number of wanted outcomes/total number of outcomes ([4])P(winning given that you are stuck)=2/4=0.5P(winning given that you switched)=2/4=0.5P(winning)=4/8=0.5P(losing)=4/8=0.5If the first choice of door is B or C, the reasoning is exactly the same as presented before. We then have 24 possible outcomes.See ([3]):Table 2
 |
| |
|
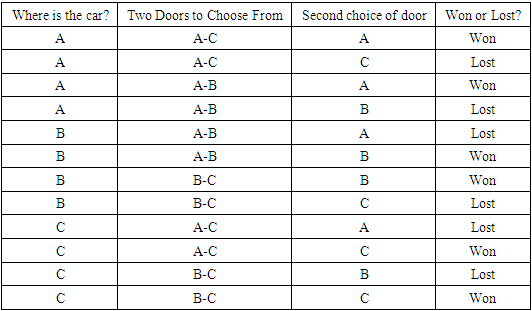
The events First Choice of Door and Monty Hall Opens are dependent ([4], [5]). P(first choice of door being A given that Monty Hall opens C)≠P(first choice of door being A) because 4/8≠8/24 or 0.5≠0.3. The events Monty Hall Opens and Second Choice of Door are independent ([4], [5]). P(second choice of door being car given that Monty Hall opens A)=P(second choice of door being car) since 4/8=12/24=0.5. P(second choice of door being car given that Monty Hall opens B)=P(second choice of door being car) since 4/8=12/24=0.5. P(second choice of door being car given that Monty Hall opens C)=P(second choice of door being car) since 4/8=12/24=0.5. P(Monty Hall opens A given that the second choice of door is a car)=P(Monty Hall opens C) because 4/12=8/24≈0.33. P(Monty Hall opens B given that the second choice of door is a car)=P(Monty Hall opens C) because 4/12=8/24≈0.33. P(Monty Hall opens C given that the second choice of door is a car)=P(Monty Hall opens C) because 4/12=8/24≈0.33. Also notice that P(winning)=P(winning given that you switched) and P(switched given that you won)=P(switched) because 12/24=6/12=0.5 and 6/12=12/24=0.5. Winning and Switched are then independent events and the right calculation is ([6]) P(W/S) = P(WՈS)/P(S) = P(W)xP(S)/P(S) = P(W) = 0.5. Following Diagram 1, we get 4/8=0.5, so the same result. If we consider the game is starting from the situation of having two doors to choose from, the table is:Table 3
 |
| |
|
We then get P(winning) = 6/12 = 0.5 and P(losing) = 6/12 = 0.5.Diagram 1 appears from assuming that P(winning given that you switched) is different from P(winning), yet we have already proven that they are equal. The formula does not apply or needs to be correctly applied. Host Opens and You Open could not be connected in the diagram because these events are independent. The tree we presented in [1] is incomplete, since it is missing stating what door conceals the car. That makes a difference because both chosen door and door concealing the car will ‘survive’ for the last round. We assumed the first chosen door concealed the car, but it is then missing counting the other cases, when it doesn’t. That will add the same amount of cases to the cake, so that we then get 24. We fixed the table presented in [7] correctly, but the table is incorrect because it treats ‘switch’ and ‘stick’ as columns but those are not actions, just a tag imposed to the second choice of the audience member, yet all other columns are actions. The right column for the reasoning appearing in [7] would be ‘you open’ and we could then have another column where we write the label associated with the ‘you open’ result, which will be ‘switched’ or ‘stuck’, when we get the same result we see in Table 2.
3. Conclusions
There is a fundamental mistake in Diagram 1, which is assuming that Winning and Switching are not independent events. We have proven, by means of adequate counting of cases, that these events are independent. With this, the probability of winning given that you switch is equal to the probability of winning, which is 0.5. [8] lets us know that “When vos Savant politely responded to a reader’s inquiry on the Monty Hall Problem, a then-relatively-unknown probability puzzle, she never could’ve imagined what would unfold: (…) she received over 10,000 letters, many from noted scholars and Ph.Ds, informing her that she was a hare-brained idiot.”
Note
1. Personal communications, 2022.
References
| [1] | Pinheiro, M (2017) “The Monty Hall Show and Murphy’s Score,” Modern International Journal of Pure and Applied Mathematics, 1(1), pp. 1–4. Available at: https://doi.org/10.5923/j.mijpam.20170101.01. |
| [2] | Lo Bello, A (1991) “Ask Marilyn: The Mathematical Controversy in Parade Magazine,” Mathematical Gazette, pp. 275–277. Available at: https://doi.org/10.2307/3619484. |
| [3] | Pinheiro, M (2022) The Monty Hall Problem and Mathematics - researchgate.net, The Monty Hall Problem and Mathematics. Research Gate. Available at: https://www.researchgate.net/publication/365852823_The_Monty_Hall_Problem_and_Mathematics (Accessed: March 10, 2023). |
| [4] | Math 101 -probability - California State University san marcos Math 101 - Probability. California State University, San Marcos. Available at: https://www.csusm.edu/stemsc/handouts/math101_probability.pdf (Accessed: March 10, 2023). |
| [5] | Khan Academy Conditional probability and independence (article), Khan Academy. Khan Academy. Available at: https://www.khanacademy.org/math/ap-statistics/probability-ap/stats-conditional-probability/a/ check-independence-conditional-probability (Accessed: March 17, 2023). |
| [6] | Libretexts (2022) 3: Basic concepts of probability, Statistics LibreTexts. Libretexts. Available at: https://stats.libretexts.org/Bookshelves/Introductory_Statistics/Book%3A_Introductory_Statistics_ (Shafer_and_Zhang)/03%3A_Basic_Concepts_of_Probability (Accessed: March 17, 2023). |
| [7] | Baumann, P. (2008). “Single-case Probabilities and the Case of Monty Hall: Levy’s View.” Synthese, 162, pp. 265–273. Available at: http://philpapers.org/rec/BAUSPA-2. |
| [8] | Crockett, Z. (2022) The time everyone "corrected" The world's smartest woman, Priceonomics. Available at: https://priceonomics.com/the-time-everyone-corrected-the-worlds-smartest/ (Accessed: March 18, 2023). |




 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML

