Dorin Mărghidanu
Corabia, Olt, România
Correspondence to: Dorin Mărghidanu, Corabia, Olt, România.
| Email: |  |
Copyright © 2020 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
The purpose of this note is to present a relation between the arithmetic mean, of a finite number of real numbers, and the arithmetic mean of their images through a convex function. Some applications of this inequality are also included.
Keywords:
Arithmetic mean, Convex function, Jensen inequality
Cite this paper: Dorin Mărghidanu, An Inequality between the Arithmetic Mean of Some Numbers and the Arithmetic Mean of Their Images through a Convex Function, Modern International Journal of Pure and Applied Mathematics, Vol. 4 No. 1, 2020, pp. 1-4. doi: 10.5923/j.mijpam.20200401.01.
1. Introduction
Let 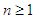 be a fixed natural number, and
be a fixed natural number, and 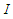 an interval of real numbers. For every
an interval of real numbers. For every 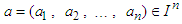 , the arithmetic mean associated to
, the arithmetic mean associated to 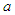 is defined as:
is defined as: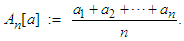 Let
Let 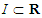 be an interval. If
be an interval. If 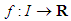 is a convex (concave) function, then the well known Jensen inequality (see [2]-[4], [10], [11] says that:
is a convex (concave) function, then the well known Jensen inequality (see [2]-[4], [10], [11] says that: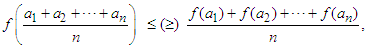 which can be written, using the above notation, as:
which can be written, using the above notation, as: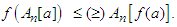 | (1.1) |
The inequality (1.1) represents a relation between the image of 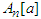 , through
, through 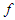 , and the arithmetic mean of the images of the numbers
, and the arithmetic mean of the images of the numbers 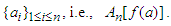 We can imagine the numbers
We can imagine the numbers 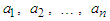 as being some data
as being some data 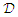 received by a statistician. For large values of
received by a statistician. For large values of 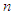 , it is hard for the statistician to look at each number,
, it is hard for the statistician to look at each number, 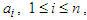 in these data. So, the statistician decides to make a skeleton of the data, composed of the minimum
in these data. So, the statistician decides to make a skeleton of the data, composed of the minimum 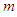 and maximum
and maximum 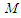 values of these data, a center
values of these data, a center 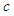 of the data, and a number
of the data, and a number 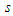 measuring the spread of the data. While
measuring the spread of the data. While 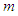 and
and 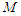 are easy to define as:
are easy to define as: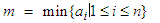 | (1.2) |
and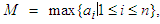 | (1.3) |
there are many different ways to define the center 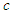 . One very popular way is to a apply first a strictly monotone function
. One very popular way is to a apply first a strictly monotone function 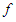 to the data
to the data 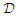 , obtaining the new data
, obtaining the new data 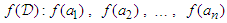 . Then we compute the average value
. Then we compute the average value 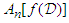 , defined as:
, defined as: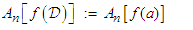 | (1.4) |
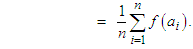 | (1.5) |
Finally, we apply the inverse function 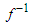 to
to 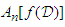 , defining the center of the data to be:
, defining the center of the data to be: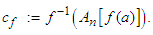 | (1.6) |
A typical example of such functions, used in computing the center of data consisting of positive numbers, is given by the functions: 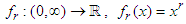 , for
, for 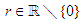 . Following the above procedure, these functions give rise to the H¨older means of the positive numbers
. Following the above procedure, these functions give rise to the H¨older means of the positive numbers 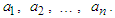 Because different functions
Because different functions 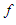 and
and 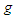 produce different centers
produce different centers 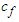 and
and 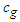 of the data, it is important to find inequalities relating
of the data, it is important to find inequalities relating 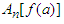 and
and 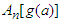 in order to understand the inequalities between
in order to understand the inequalities between 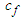 and
and 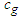 .
.
2. Main Result
We present now the result leading to the main result of this note.Proposition 2.1 If1. 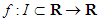 is a convex (concave) function;2.
is a convex (concave) function;2. 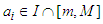 , for all
, for all 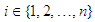 , where
, where 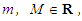 then the following inequality:
then the following inequality: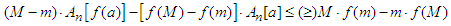 | (2.7) |
holds.Proof. Let 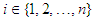 be fixed. Since
be fixed. Since 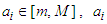 can be written as the following convex combination of
can be written as the following convex combination of 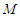 and
and 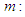
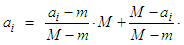 If we denote
If we denote 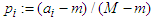 and
and 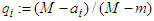 , then since
, then since 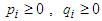 , and
, and 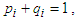 we conclude from the definition of convexity of
we conclude from the definition of convexity of 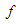 , that:
, that: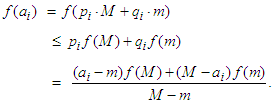 | (2.8) |
Summing up in the last inequality from 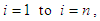 we obtain:
we obtain: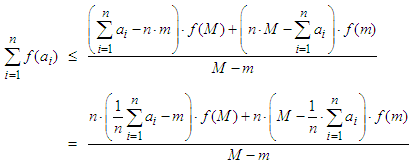 After multiplying both sides of the last relation by
After multiplying both sides of the last relation by 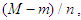 we obtain:
we obtain: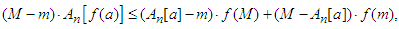 which is equivalent to:
which is equivalent to: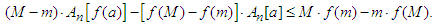 If
If 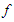 is concave all the inequalities from this proof are reversed.Corollary 2.2. If we impose the additional condition that
is concave all the inequalities from this proof are reversed.Corollary 2.2. If we impose the additional condition that 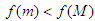 to the assumptions from Proposition 2.1, then:
to the assumptions from Proposition 2.1, then: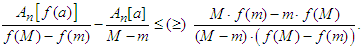 | (2.9) |
Proof. Since 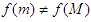 , we have
, we have 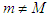 . Dividing both sides of the inequality (2.7) by the strictly positive number
. Dividing both sides of the inequality (2.7) by the strictly positive number 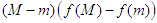 , we obtain (2.9).Theorem 2.3 Let
, we obtain (2.9).Theorem 2.3 Let  be real numbers,
be real numbers, 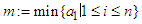 and
and 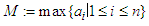 . Let
. Let 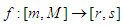 and
and 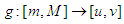 , be two strictly increasing and bijective functions, such that:
, be two strictly increasing and bijective functions, such that: 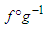 is convex on
is convex on 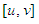 . Then:
. Then: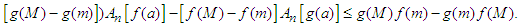 | (2.10) |
Proof. We apply Proposition 2.1 to the numbers: 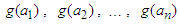 and the convex function
and the convex function 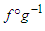 obtaining inequality (2.10).Application 2.4 Let
obtaining inequality (2.10).Application 2.4 Let 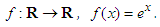 It is clear that
It is clear that 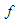 is convex and strictly increasing on
is convex and strictly increasing on 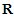 . Thus for all
. Thus for all 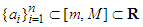 , such that
, such that 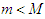 , we conclude from (2.9), that:
, we conclude from (2.9), that: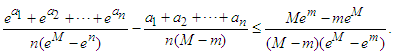 | (2.11) |
If 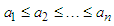 , with at least one of these inequalities being strict, then setting:
, with at least one of these inequalities being strict, then setting: 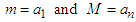 , we can rewrite (2.11) as:
, we can rewrite (2.11) as: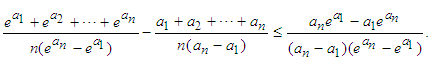 | (2.12) |
Corollary 2.5 If 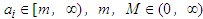 , for all
, for all 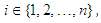 then:
then: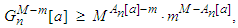 where
where 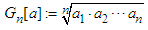 is the geometric mean of the numbers
is the geometric mean of the numbers 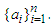 Proof. Since the function
Proof. Since the function 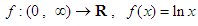 is concave, it follows from the inequality (2.7) that:
is concave, it follows from the inequality (2.7) that: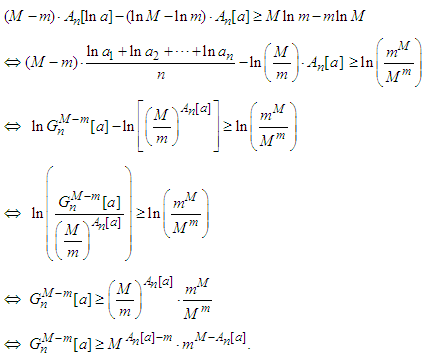 If
If 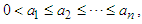 then we can take
then we can take 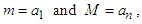 and obtain:
and obtain: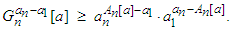 | (2.13) |
This inequality holds even when 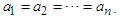 Application 2.6 Let
Application 2.6 Let 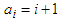 , for all
, for all 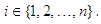 Then we can take
Then we can take 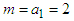 and
and 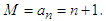 We have:
We have: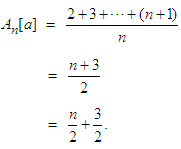 It follows now from (2.13) that:
It follows now from (2.13) that: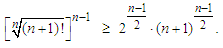 This is equivalent to:
This is equivalent to: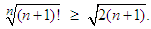 Corollary 2.7 If
Corollary 2.7 If 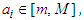 for all
for all 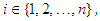 and
and 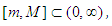 then:
then: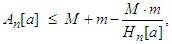 | (2.14) |
where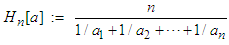 is the harmonic mean of the numbers
is the harmonic mean of the numbers  Proof. The function
Proof. The function 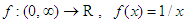 is convex. Applying the inequality (2.7) to this function, we get:
is convex. Applying the inequality (2.7) to this function, we get: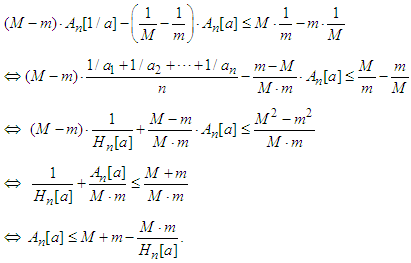 If
If 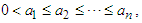 then by taking
then by taking 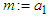 and
and 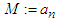 in (2.14), we obtain:
in (2.14), we obtain: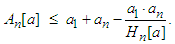 Alternative characterizations for means, obtained by different methods, can be found in [6]-[9].Observation 2.8 The means
Alternative characterizations for means, obtained by different methods, can be found in [6]-[9].Observation 2.8 The means 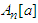 and
and 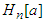 make sense for negative numbers, too. If
make sense for negative numbers, too. If 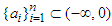 , then the inequality (2.14) is reversed, which can be proved very simply by multiplying both sides of this inequality by -1.Application 2.9 Let
, then the inequality (2.14) is reversed, which can be proved very simply by multiplying both sides of this inequality by -1.Application 2.9 Let 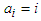 , for all
, for all 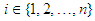 . Then we can take
. Then we can take 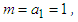
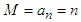 , and we have
, and we have 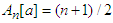 . It follows now from (2.14) that:
. It follows now from (2.14) that: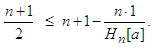 This is equivalent to
This is equivalent to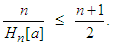 The last inequality means:
The last inequality means: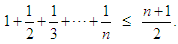 Corollary 2.10 Let
Corollary 2.10 Let 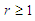 and
and 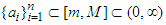 . Then the following inequality holds:
. Then the following inequality holds: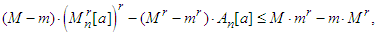 | (2.15) |
where: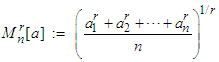 is the power mean of order
is the power mean of order 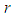 (called also the H¨older mean of order
(called also the H¨older mean of order 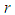 ) of the numbers
) of the numbers 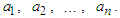 In particular if
In particular if 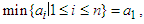
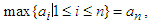 and
and 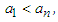 then:
then: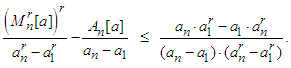 | (2.16) |
Proof. Everything follow by applying the inequality (2.7) to the convex and increasing function 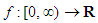 ,
, 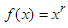 .Application 2.11 For all
.Application 2.11 For all 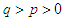 and all positive numbers
and all positive numbers 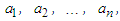 we have:
we have: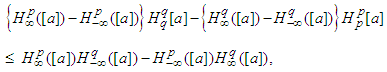 where
where 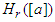 denotes the
denotes the 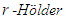 mean of
mean of 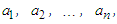 for all
for all 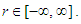 Proof. We simply apply Theorem 2.3 to the numbers
Proof. We simply apply Theorem 2.3 to the numbers 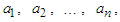 and the function
and the function 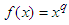 and
and 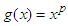 . We have
. We have 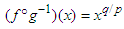 , which is a convex function since
, which is a convex function since 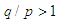 , and thus the result of our application follows easily.Observation 2.12 All the inequalities from this paper can be reformulated using weighted means, too.
, and thus the result of our application follows easily.Observation 2.12 All the inequalities from this paper can be reformulated using weighted means, too.
ACKNOWLEDGEMENTS
• The author would like to thank the referees for their kind comments and suggestions that greatly helped him in improving the quality of this paper.• The author would also like to thank Professor Aurel I. Stan, from The Ohio State University, for helping him in preparing this manuscript.
References
| [1] |  and Pop T. O., “A generalization of Radon’s in- equality”, Creative Math. & Inf. 20, No. 2, 2011. and Pop T. O., “A generalization of Radon’s in- equality”, Creative Math. & Inf. 20, No. 2, 2011. |
| [2] | Beckenbach, E.F. and Bellman, R., “Inequalities”, Springer–Verlag, Berlin–Heidelberg– New–York, 1961. |
| [3] | Bullen, P.S.,  P.M., “Means and Their Inequalities”, D. Reidel Publishing Company, Dordrecht/Boston, 1988. P.M., “Means and Their Inequalities”, D. Reidel Publishing Company, Dordrecht/Boston, 1988. |
| [4] | Bullen, P.S., “Handbook of Means and Their Inequalities”, Kluwer Academic Publishers, Dordrecht/Boston/London, 2003. |
| [5] | Cerone P.D. and Dragomir S.S., “Mathematical Inequalities: A Perspective”, CRC Press, Taylor & Francis Group, 2011. |
| [6] |  and Bencze M., “Inequalities for Differences of Means, deduced from the Inequality and Bencze M., “Inequalities for Differences of Means, deduced from the Inequality  in ((OCTOGON Mathematical Magazine)), Vol. 12, No. 2.A., pp. 532–539, October, 2004. in ((OCTOGON Mathematical Magazine)), Vol. 12, No. 2.A., pp. 532–539, October, 2004. |
| [7] |  Diaz-Barrero, J.L. and Rădulescu, S., “New refinements of some classical inequalities”, Math. Inequal. and Appl., Volume 12 , Number 3, pp. 513-518, July, 2009. Diaz-Barrero, J.L. and Rădulescu, S., “New refinements of some classical inequalities”, Math. Inequal. and Appl., Volume 12 , Number 3, pp. 513-518, July, 2009. |
| [8] |  “Refinements of classical means inequality via cyclic mixed means”, in ((OCTOGON Mathematical Magazine)), Vol.27, No. 2, pp. 814-823, October, 2019. “Refinements of classical means inequality via cyclic mixed means”, in ((OCTOGON Mathematical Magazine)), Vol.27, No. 2, pp. 814-823, October, 2019. |
| [9] |  “Reverese inequality of Huygens and some framing with means”, in ((Romanian Mathematical Magazine)), 2020. Online publication: http://r6a.cn/by5A. “Reverese inequality of Huygens and some framing with means”, in ((Romanian Mathematical Magazine)), 2020. Online publication: http://r6a.cn/by5A. |
| [10] | Mitrinović, D.S. (in cooperation with Vasić, P.M.), “Analytic Inequalities”, Band 165, Springer–Verlag, Berlin, 1970. |
| [11] | Mitrinović, D.S., Pecaric, J.E., and Fink, A.M., “Classical and New Inequalities in Analysis”, Kluwer Acad. Press, 1993. |


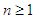 be a fixed natural number, and
be a fixed natural number, and 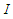 an interval of real numbers. For every
an interval of real numbers. For every 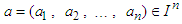 , the arithmetic mean associated to
, the arithmetic mean associated to 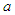 is defined as:
is defined as: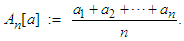 Let
Let 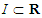 be an interval. If
be an interval. If 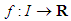 is a convex (concave) function, then the well known Jensen inequality (see [2]-[4], [10], [11] says that:
is a convex (concave) function, then the well known Jensen inequality (see [2]-[4], [10], [11] says that: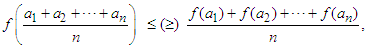 which can be written, using the above notation, as:
which can be written, using the above notation, as: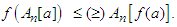
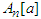 , through
, through 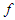 , and the arithmetic mean of the images of the numbers
, and the arithmetic mean of the images of the numbers 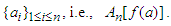 We can imagine the numbers
We can imagine the numbers 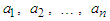 as being some data
as being some data 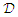 received by a statistician. For large values of
received by a statistician. For large values of 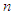 , it is hard for the statistician to look at each number,
, it is hard for the statistician to look at each number, 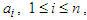 in these data. So, the statistician decides to make a skeleton of the data, composed of the minimum
in these data. So, the statistician decides to make a skeleton of the data, composed of the minimum 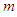 and maximum
and maximum 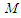 values of these data, a center
values of these data, a center 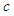 of the data, and a number
of the data, and a number 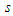 measuring the spread of the data. While
measuring the spread of the data. While 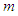 and
and 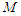 are easy to define as:
are easy to define as: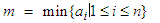
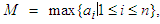
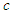 . One very popular way is to a apply first a strictly monotone function
. One very popular way is to a apply first a strictly monotone function 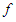 to the data
to the data 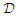 , obtaining the new data
, obtaining the new data 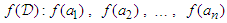 . Then we compute the average value
. Then we compute the average value 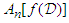 , defined as:
, defined as: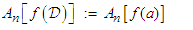
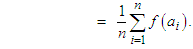
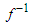 to
to 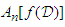 , defining the center of the data to be:
, defining the center of the data to be: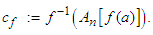
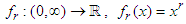 , for
, for 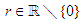 . Following the above procedure, these functions give rise to the H¨older means of the positive numbers
. Following the above procedure, these functions give rise to the H¨older means of the positive numbers 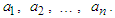 Because different functions
Because different functions 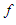 and
and 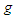 produce different centers
produce different centers 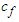 and
and 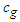 of the data, it is important to find inequalities relating
of the data, it is important to find inequalities relating 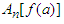 and
and 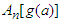 in order to understand the inequalities between
in order to understand the inequalities between 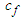 and
and 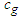 .
.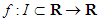 is a convex (concave) function;2.
is a convex (concave) function;2. 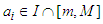 , for all
, for all 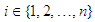 , where
, where 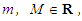 then the following inequality:
then the following inequality: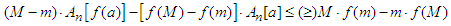
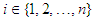 be fixed. Since
be fixed. Since 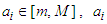 can be written as the following convex combination of
can be written as the following convex combination of 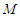 and
and 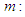
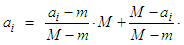 If we denote
If we denote 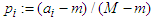 and
and 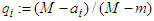 , then since
, then since 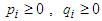 , and
, and 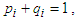 we conclude from the definition of convexity of
we conclude from the definition of convexity of 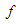 , that:
, that: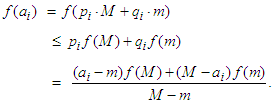
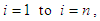 we obtain:
we obtain: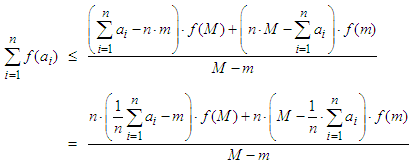 After multiplying both sides of the last relation by
After multiplying both sides of the last relation by 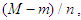 we obtain:
we obtain: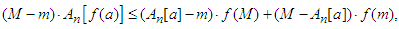 which is equivalent to:
which is equivalent to: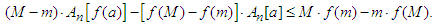 If
If 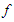 is concave all the inequalities from this proof are reversed.Corollary 2.2. If we impose the additional condition that
is concave all the inequalities from this proof are reversed.Corollary 2.2. If we impose the additional condition that 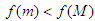 to the assumptions from Proposition 2.1, then:
to the assumptions from Proposition 2.1, then: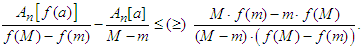
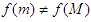 , we have
, we have 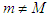 . Dividing both sides of the inequality (2.7) by the strictly positive number
. Dividing both sides of the inequality (2.7) by the strictly positive number 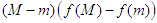 , we obtain (2.9).Theorem 2.3 Let
, we obtain (2.9).Theorem 2.3 Let  be real numbers,
be real numbers, 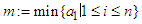 and
and 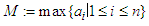 . Let
. Let 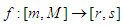 and
and 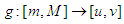 , be two strictly increasing and bijective functions, such that:
, be two strictly increasing and bijective functions, such that: 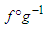 is convex on
is convex on 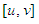 . Then:
. Then: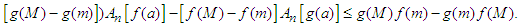
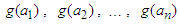 and the convex function
and the convex function 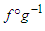 obtaining inequality (2.10).Application 2.4 Let
obtaining inequality (2.10).Application 2.4 Let 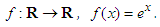 It is clear that
It is clear that 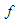 is convex and strictly increasing on
is convex and strictly increasing on 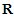 . Thus for all
. Thus for all 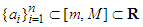 , such that
, such that 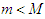 , we conclude from (2.9), that:
, we conclude from (2.9), that: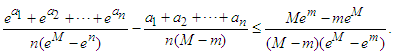
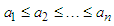 , with at least one of these inequalities being strict, then setting:
, with at least one of these inequalities being strict, then setting: 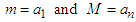 , we can rewrite (2.11) as:
, we can rewrite (2.11) as: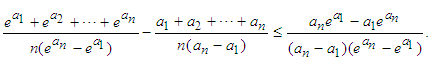
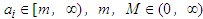 , for all
, for all 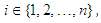 then:
then: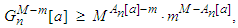 where
where 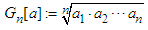 is the geometric mean of the numbers
is the geometric mean of the numbers 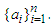 Proof. Since the function
Proof. Since the function 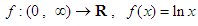 is concave, it follows from the inequality (2.7) that:
is concave, it follows from the inequality (2.7) that: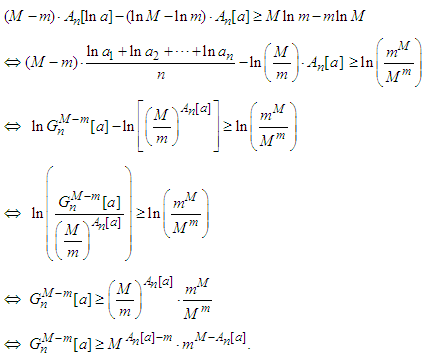 If
If 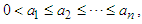 then we can take
then we can take 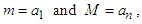 and obtain:
and obtain: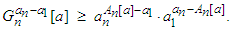
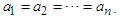 Application 2.6 Let
Application 2.6 Let 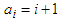 , for all
, for all 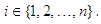 Then we can take
Then we can take 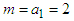 and
and 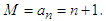 We have:
We have: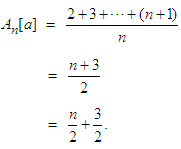 It follows now from (2.13) that:
It follows now from (2.13) that: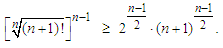 This is equivalent to:
This is equivalent to: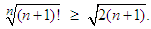 Corollary 2.7 If
Corollary 2.7 If 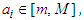 for all
for all 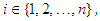 and
and 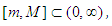 then:
then: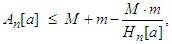
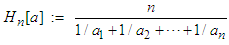 is the harmonic mean of the numbers
is the harmonic mean of the numbers 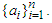 Proof. The function
Proof. The function 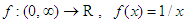 is convex. Applying the inequality (2.7) to this function, we get:
is convex. Applying the inequality (2.7) to this function, we get: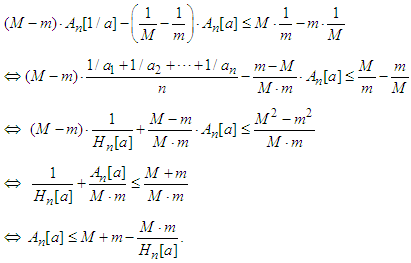 If
If 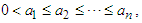 then by taking
then by taking 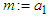 and
and 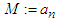 in (2.14), we obtain:
in (2.14), we obtain: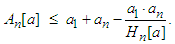 Alternative characterizations for means, obtained by different methods, can be found in [6]-[9].Observation 2.8 The means
Alternative characterizations for means, obtained by different methods, can be found in [6]-[9].Observation 2.8 The means 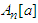 and
and 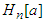 make sense for negative numbers, too. If
make sense for negative numbers, too. If 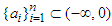 , then the inequality (2.14) is reversed, which can be proved very simply by multiplying both sides of this inequality by -1.Application 2.9 Let
, then the inequality (2.14) is reversed, which can be proved very simply by multiplying both sides of this inequality by -1.Application 2.9 Let 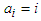 , for all
, for all 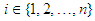 . Then we can take
. Then we can take 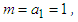
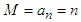 , and we have
, and we have 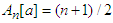 . It follows now from (2.14) that:
. It follows now from (2.14) that: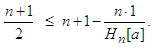 This is equivalent to
This is equivalent to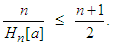 The last inequality means:
The last inequality means: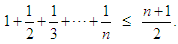 Corollary 2.10 Let
Corollary 2.10 Let 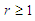 and
and 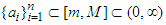 . Then the following inequality holds:
. Then the following inequality holds: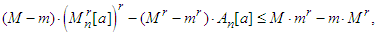
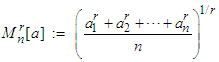 is the power mean of order
is the power mean of order 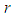 (called also the H¨older mean of order
(called also the H¨older mean of order 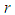 ) of the numbers
) of the numbers 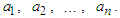 In particular if
In particular if 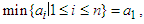
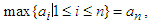 and
and 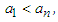 then:
then: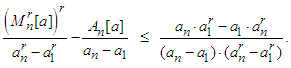
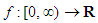 ,
, 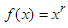 .Application 2.11 For all
.Application 2.11 For all 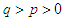 and all positive numbers
and all positive numbers 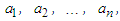 we have:
we have: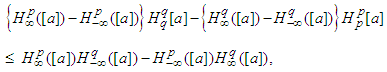 where
where 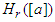 denotes the
denotes the 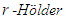 mean of
mean of 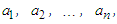 for all
for all 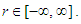 Proof. We simply apply Theorem 2.3 to the numbers
Proof. We simply apply Theorem 2.3 to the numbers 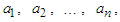 and the function
and the function 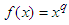 and
and 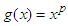 . We have
. We have 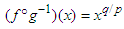 , which is a convex function since
, which is a convex function since 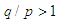 , and thus the result of our application follows easily.Observation 2.12 All the inequalities from this paper can be reformulated using weighted means, too.
, and thus the result of our application follows easily.Observation 2.12 All the inequalities from this paper can be reformulated using weighted means, too. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML and Pop T. O., “A generalization of Radon’s in- equality”, Creative Math. & Inf. 20, No. 2, 2011.
and Pop T. O., “A generalization of Radon’s in- equality”, Creative Math. & Inf. 20, No. 2, 2011. P.M., “Means and Their Inequalities”, D. Reidel Publishing Company, Dordrecht/Boston, 1988.
P.M., “Means and Their Inequalities”, D. Reidel Publishing Company, Dordrecht/Boston, 1988. and Bencze M., “Inequalities for Differences of Means, deduced from the Inequality
and Bencze M., “Inequalities for Differences of Means, deduced from the Inequality  in ((OCTOGON Mathematical Magazine)), Vol. 12, No. 2.A., pp. 532–539, October, 2004.
in ((OCTOGON Mathematical Magazine)), Vol. 12, No. 2.A., pp. 532–539, October, 2004. Diaz-Barrero, J.L. and Rădulescu, S., “New refinements of some classical inequalities”, Math. Inequal. and Appl., Volume 12 , Number 3, pp. 513-518, July, 2009.
Diaz-Barrero, J.L. and Rădulescu, S., “New refinements of some classical inequalities”, Math. Inequal. and Appl., Volume 12 , Number 3, pp. 513-518, July, 2009. “Refinements of classical means inequality via cyclic mixed means”, in ((OCTOGON Mathematical Magazine)), Vol.27, No. 2, pp. 814-823, October, 2019.
“Refinements of classical means inequality via cyclic mixed means”, in ((OCTOGON Mathematical Magazine)), Vol.27, No. 2, pp. 814-823, October, 2019. “Reverese inequality of Huygens and some framing with means”, in ((Romanian Mathematical Magazine)), 2020. Online publication: http://r6a.cn/by5A.
“Reverese inequality of Huygens and some framing with means”, in ((Romanian Mathematical Magazine)), 2020. Online publication: http://r6a.cn/by5A.