-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Modern International Journal of Pure and Applied Mathematics
2019; 3(1): 1-8
doi:10.5923/j.mijpam.20190301.01

Comellas’ Deterministic Small-Worlds: A Review
Marcia R. Pinheiro
IICSE University, USA
Correspondence to: Marcia R. Pinheiro , IICSE University, USA.
| Email: |  |
Copyright © 2019 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

In this piece, the paper Deterministic Small-world Communication Networks, a paper from the year of 2000 by Comellas, Ozon, and Peters, is discussed. From the introduction, where some mismatch between sigmatoids, and intended senses is identified, to the conclusion, where the same mismatch appears in the shape of wonder, the findings are of surprising nature: major misunderstandings in the interpretation of the research or teaching or invention of others may lead to great new theories, which may lead to wonderful sets of new, and meaningful mathematical paradigms.
Keywords: Small-world, Comellas, Network, Deterministic
Cite this paper: Marcia R. Pinheiro , Comellas’ Deterministic Small-Worlds: A Review, Modern International Journal of Pure and Applied Mathematics, Vol. 3 No. 1, 2019, pp. 1-8. doi: 10.5923/j.mijpam.20190301.01.
1. Introduction
- “No one set out to invent sticky notes. Instead, in 1968, Dr. Spencer Silver, a chemist at 3M Company, invented a unique, low-tack adhesive that would stick to things but also could be repositioned multiple times. He was trying to invent a super-strong adhesive, but he came up with a super-weak one instead”
 (National Center for Families Learning 2018, para. 5)Comellas et al. happened to create a new graph, which is a variation of the Circulant Graph, which was seen before in Algebra through matrices:
(National Center for Families Learning 2018, para. 5)Comellas et al. happened to create a new graph, which is a variation of the Circulant Graph, which was seen before in Algebra through matrices:
 (Lindner 2018, p. 1)
(Lindner 2018, p. 1)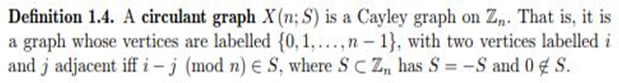
 (Morris 2004, p. 2)
(Morris 2004, p. 2)
 (Parsons 1980)
(Parsons 1980)
 (Comellas, Ozon, & Peters 2000, p. 84)The original circulant graph, which connects to the matrix exhibited above:
(Comellas, Ozon, & Peters 2000, p. 84)The original circulant graph, which connects to the matrix exhibited above: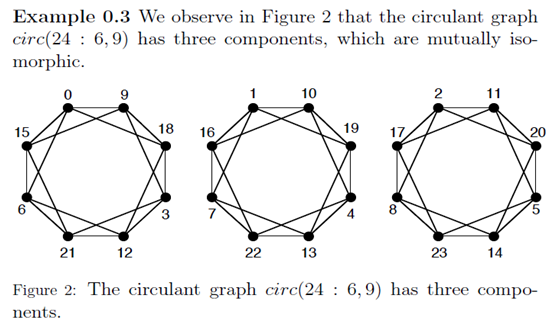
 (Alspach 2010, para. 16)Because the name above coincides with the name chosen by Comellas et al., Circulant Graph, we may think that Comellas et al. would have to have the same sort of symbol to represent this graph, so circ(x: y,w). In this case, there is hope that his symbol, Cm,n will lead to another type of graph because the graph above is certainly not Comellas’ Circulant (two reference numbers, not three). Let’s see:
(Alspach 2010, para. 16)Because the name above coincides with the name chosen by Comellas et al., Circulant Graph, we may think that Comellas et al. would have to have the same sort of symbol to represent this graph, so circ(x: y,w). In this case, there is hope that his symbol, Cm,n will lead to another type of graph because the graph above is certainly not Comellas’ Circulant (two reference numbers, not three). Let’s see: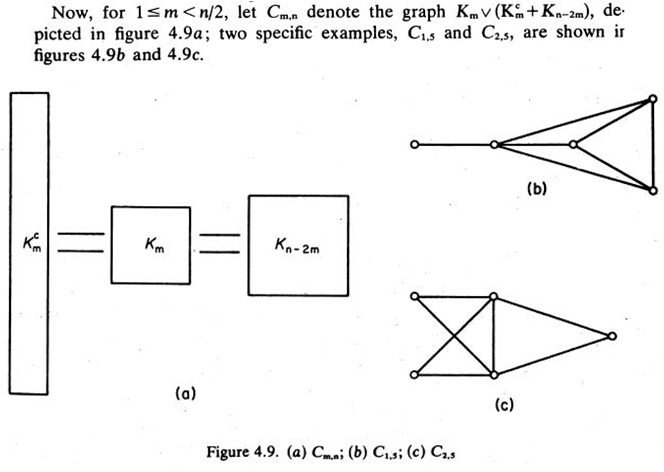
 (Bondy & Murty 1976, p. 58)It looks like Comellas et al. have created a new type of graph, which, in many senses, relates to the Circulant Graph, but, in many other senses, does not. In the sections that follow, we discuss the originality of Comellas et al.’s graph together with the ideas exposed in the mentioned scientific article.
(Bondy & Murty 1976, p. 58)It looks like Comellas et al. have created a new type of graph, which, in many senses, relates to the Circulant Graph, but, in many other senses, does not. In the sections that follow, we discuss the originality of Comellas et al.’s graph together with the ideas exposed in the mentioned scientific article. 2. Development
- Comellas et al. (2000) start this paper, on page 83, with the following paragraph:“Small-world networks were introduced by Watts and Strogatz in a recent paper [9] as models of real world situations including electric power grids, the spread of diseases in populations, the collaboration networks of film actors, and the neural network of the worm Caenorhabditis elegans [8,9].”He was then referring to the article published in Nature:
 Small-world networks were actually introduced by Milgram (1969) - an American psychologist who lived from 1933 to 1984 - in his paper, An Experimental Study of the Small World Problem.Watts and Strogatz (1998) did mention the small-world phenomenon in their article with Nature about 14 years after the death of Milgram, but the novelty then consisted of the sigmatoids (Pinheiro 2018, p. 38) appearing together, small-world network, or of the world reference (Pinheiro 2018, p. 38) for the expression, now a particular mathematical/statistical model.
Small-world networks were actually introduced by Milgram (1969) - an American psychologist who lived from 1933 to 1984 - in his paper, An Experimental Study of the Small World Problem.Watts and Strogatz (1998) did mention the small-world phenomenon in their article with Nature about 14 years after the death of Milgram, but the novelty then consisted of the sigmatoids (Pinheiro 2018, p. 38) appearing together, small-world network, or of the world reference (Pinheiro 2018, p. 38) for the expression, now a particular mathematical/statistical model.  Still from the first page of Comellas et al.’s article (page 83) is the extract above: in this case, the observation is that if one is structured, then the other should be non-structured instead of random, and here we are just following what could be called ‘the peasant’s logic’. Random networks could make sense from a generative point of view: computers generating those connections randomly. Notwithstanding, once the networks are formed, and we are able to photograph those, it seems undeniable that non-structured or irregular would be more appropriate. At the same time, why would ‘structured’ make more sense than regular even in normal language? All models have structure.
Still from the first page of Comellas et al.’s article (page 83) is the extract above: in this case, the observation is that if one is structured, then the other should be non-structured instead of random, and here we are just following what could be called ‘the peasant’s logic’. Random networks could make sense from a generative point of view: computers generating those connections randomly. Notwithstanding, once the networks are formed, and we are able to photograph those, it seems undeniable that non-structured or irregular would be more appropriate. At the same time, why would ‘structured’ make more sense than regular even in normal language? All models have structure. 
 (Wolfrang Research, Inc. 2018, para. 1)
(Wolfrang Research, Inc. 2018, para. 1)
 (Brainasoft 2018, para. 1-3)Circulant Graphs may be studied from inside of Pure Geometry (Carlson (2018). There, the terms regular, and irregular seem to be proper.It is important to understand that Professor Comellas, and his group started precursor work: they started to change what was exclusively of statistical nature into what would be exclusively of mathematical nature (Pinheiro 2012, p. 261). As a consequence, everything was restarted, and therefore it takes a great amount of reflection to build the best lingo, objects, definitions, and all else.
(Brainasoft 2018, para. 1-3)Circulant Graphs may be studied from inside of Pure Geometry (Carlson (2018). There, the terms regular, and irregular seem to be proper.It is important to understand that Professor Comellas, and his group started precursor work: they started to change what was exclusively of statistical nature into what would be exclusively of mathematical nature (Pinheiro 2012, p. 261). As a consequence, everything was restarted, and therefore it takes a great amount of reflection to build the best lingo, objects, definitions, and all else. 
 (Comellas, Ozon, & Peters 2000, p. 84)The main issue is that small-world connects to the research of Professor Milgram, and his definition of small world is 64 in 296 chains present an average of six edges of distance (Pinheiro 2016, p. 270) or around 64 nodes (also smaller), which means being able to go from one end to another through only a few edges (his average was 5.2) or having around 64 nodes in the network. The network itself does not change: what changes is the way of studying or describing it. One way is statistical, and therefore is a way to deal with the random events of human life, and this world when predicting future changes. Another way is mathematical, and therefore is a way to deal with the networks as they are at the moment of the analysis, so without considering that things may change in the near future, that is, that connections may be added, may disappear, and so on. In this case, deterministic means mathematical, and therefore, if we are working from inside of the World of Mathematics, the expression ‘deterministic small-world networks’ can be replaced with ‘small-world networks’.If it is inside of Mathematics, ‘networks of maximum diameter 6, and at most 64 nodes’ would be a good choice. Then, again, why would they not be just networks?
(Comellas, Ozon, & Peters 2000, p. 84)The main issue is that small-world connects to the research of Professor Milgram, and his definition of small world is 64 in 296 chains present an average of six edges of distance (Pinheiro 2016, p. 270) or around 64 nodes (also smaller), which means being able to go from one end to another through only a few edges (his average was 5.2) or having around 64 nodes in the network. The network itself does not change: what changes is the way of studying or describing it. One way is statistical, and therefore is a way to deal with the random events of human life, and this world when predicting future changes. Another way is mathematical, and therefore is a way to deal with the networks as they are at the moment of the analysis, so without considering that things may change in the near future, that is, that connections may be added, may disappear, and so on. In this case, deterministic means mathematical, and therefore, if we are working from inside of the World of Mathematics, the expression ‘deterministic small-world networks’ can be replaced with ‘small-world networks’.If it is inside of Mathematics, ‘networks of maximum diameter 6, and at most 64 nodes’ would be a good choice. Then, again, why would they not be just networks? 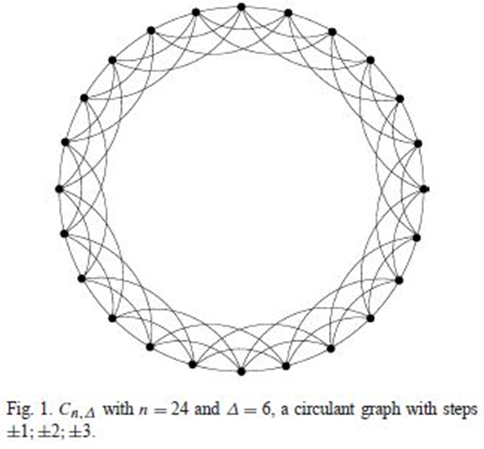 This picture appears on page 84 of Comellas et al.’s article. It then lets us know that his circulant does not comply with the definition of circulant that existed until that year, 2000. Notice that nodes are 24, but only 6 links exist for each node. In this case, Comellas et al. did not notice, but they effectively created a new model to describe, and study networks, a variation of the circulant graph that needs an original name. In the section number 5, Comellas et al. make comparisons between the analytical, and the numerical approaches. They then conclude that adding star graphs instead of double loops is wiser if the objective is creating something similar to a small-world real-life situation. The issue that appears here is that the decision should be clear: if the intention was changing all that was probabilistic, and therefore more of statistical, or real-life nature, into what is deterministic, and therefore more of mathematical, or machine-like nature, then there is no need to ‘approach the real-life data’, since works depart from the final situation.Perhaps the value of this part of their study is in attempting to observe, and control the dynamics involved when the network goes from not-so-connected to small-world, and therefore understanding things from a sociological point of view: how are these people connecting to each other as time advances?The problem then becomes that they are computer simulations, not real data. There are also criticisms of mathematical nature to this piece. The extract below came from (Pinheiro 2007, pp. 1063-1064):
This picture appears on page 84 of Comellas et al.’s article. It then lets us know that his circulant does not comply with the definition of circulant that existed until that year, 2000. Notice that nodes are 24, but only 6 links exist for each node. In this case, Comellas et al. did not notice, but they effectively created a new model to describe, and study networks, a variation of the circulant graph that needs an original name. In the section number 5, Comellas et al. make comparisons between the analytical, and the numerical approaches. They then conclude that adding star graphs instead of double loops is wiser if the objective is creating something similar to a small-world real-life situation. The issue that appears here is that the decision should be clear: if the intention was changing all that was probabilistic, and therefore more of statistical, or real-life nature, into what is deterministic, and therefore more of mathematical, or machine-like nature, then there is no need to ‘approach the real-life data’, since works depart from the final situation.Perhaps the value of this part of their study is in attempting to observe, and control the dynamics involved when the network goes from not-so-connected to small-world, and therefore understanding things from a sociological point of view: how are these people connecting to each other as time advances?The problem then becomes that they are computer simulations, not real data. There are also criticisms of mathematical nature to this piece. The extract below came from (Pinheiro 2007, pp. 1063-1064):
3. Conclusions
- Professor Comellas, and his group seem to have found another graph, different from the Circulant Graph, which was also part of Algebra through the Circulant Matrix. They use similar elements to describe, and work with their own graphs, but the graphs are distinct, since the number of columns, and rows of the matrices does not equate the number of vertices of the graph.The expression ‘deterministic small-world networks’ does not make much sense because ‘deterministic’ comes from changing what was statistical into what is mathematical, and there, in Mathematics, all is deterministic. The expression ‘small-world networks’ cannot make much sense in Mathematics: all should be absolutely determined, so perhaps we say networks of size of about 64 nodes, and with a maximum diameter of 6. In this case, since the Mathematics used is the same (small or large networks), it looks like we should simply refer to the graph that is formed instead: Comellas’ Circulant.We then have regular, and irregular Comellas’ circulants: regular circulants of this type would bring vertices that have, all of them, the same degree.Some small technical details are worth the note: Comellas et al. missed a constraint that is necessary for their theorems, and lemmas to be valid. If, in Cn,δ, n is the number of vertices, and δ is the number of links per vertex, then δ < 2n/3.Comparing numerical results with analytical data cannot make sense, or it is only part of the needed work, because they are both purely abstract in nature: we need to compare one of those results (numerical or analytical), or even both, to the studies on the Bacon number (Wolfram Demonstrations Project & Contributors 2019, para. 1-2) or Milgram’s letters (Milgram 1969). The whole interest seems to then be to the side of defining small worlds in a mathematical way (Pinheiro 2018b), and studying step by step the process of ‘wiring’ between humans from a selected group.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML