-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Modern International Journal of Pure and Applied Mathematics
2018; 2(1): 1-4
doi:10.5923/j.mijpam.20180201.01

Really Short Note on Examples of S-convex Functions
M. R. Pinheiro
IICSE University, USA
Correspondence to: M. R. Pinheiro, IICSE University, USA.
| Email: |  |
Copyright © 2018 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

In this note, we present a few more important scientific remarks regarding the S-convexity phenomenon. This time, we talk about examples. That was one of the first queries Professor Mark Nelson had for us at the ANZIAM meeting that happened this year, in 2017, at the Wollongong University, Information Sciences building. We here talk about a very trivial example. Yet this example will prove a few really old results to be equivocated.
Keywords: Noindent Analysis, S-convexity, Example
Cite this paper: M. R. Pinheiro, Really Short Note on Examples of S-convex Functions, Modern International Journal of Pure and Applied Mathematics, Vol. 2 No. 1, 2018, pp. 1-4. doi: 10.5923/j.mijpam.20180201.01.
1. Introduction
- We have just presented the new definition for the phenomenon S-convexity at the ANZIAM meeting. Our talk was named Time to Think of S-convexity [1]. The new definition is:Definition 1. A function
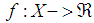 , where
, where 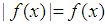 , is told to belong to
, is told to belong to  if the inequality
if the inequality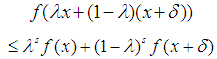 holds
holds 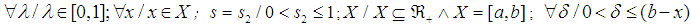 .Definition 2. A function
.Definition 2. A function 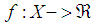 , where
, where  , is told to belong to
, is told to belong to  if the inequality
if the inequality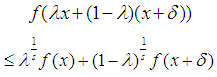 holds
holds  .Remark 1. If the inequality is obeyed in the supplementary1 situation by f , then f is said to be
.Remark 1. If the inequality is obeyed in the supplementary1 situation by f , then f is said to be  concave.This definition includes the essence of
concave.This definition includes the essence of  -convexity as presented by Hudzik and Maligranda [2].In this really short note, we will be proving that
-convexity as presented by Hudzik and Maligranda [2].In this really short note, we will be proving that 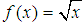 belongs to
belongs to 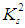 as we now define it, and, with this, we will be proving that some of the claims from [3] are unfounded.
as we now define it, and, with this, we will be proving that some of the claims from [3] are unfounded.2. Development
- Assume that it is not the case that
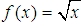 is
is 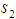 -convex. That means that it is possible to find at least one value for a or b or even for
-convex. That means that it is possible to find at least one value for a or b or even for 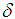 or x such that it is not true that
or x such that it is not true that 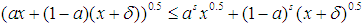 . In this case, we know that (A)
. In this case, we know that (A) 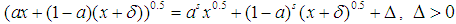 . a can always assume the value 0. If we replace a with 0 in
. a can always assume the value 0. If we replace a with 0 in  , however, we get that
, however, we get that 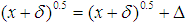 . The last equation implies that
. The last equation implies that 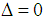 , but this is a contradiction with our assumptions and therefore proves that our assumptions are equivocated. That leads us to the desired result, since the mistake was assuming that
, but this is a contradiction with our assumptions and therefore proves that our assumptions are equivocated. That leads us to the desired result, since the mistake was assuming that 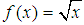 was not part of
was not part of 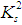 .The extract we see below this line came from [3].
.The extract we see below this line came from [3].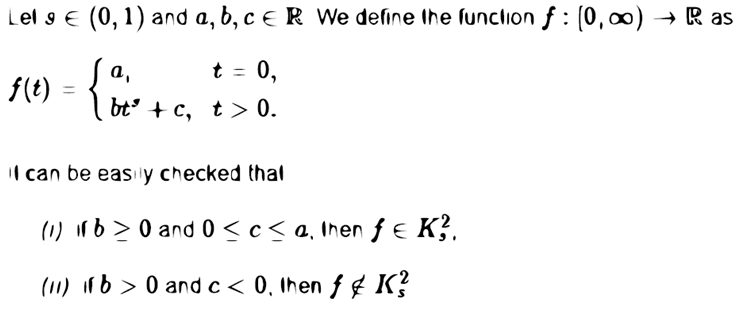 | Figure 1. Hudzik and Maligranda's theorem to generate examples |
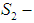 convexity: It is just a matter of saying that x is now greater than 1. In this case,
convexity: It is just a matter of saying that x is now greater than 1. In this case, 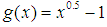 does belong to
does belong to 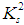 , but, according to the Figure 1, that could not be true
, but, according to the Figure 1, that could not be true 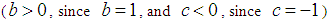 .
.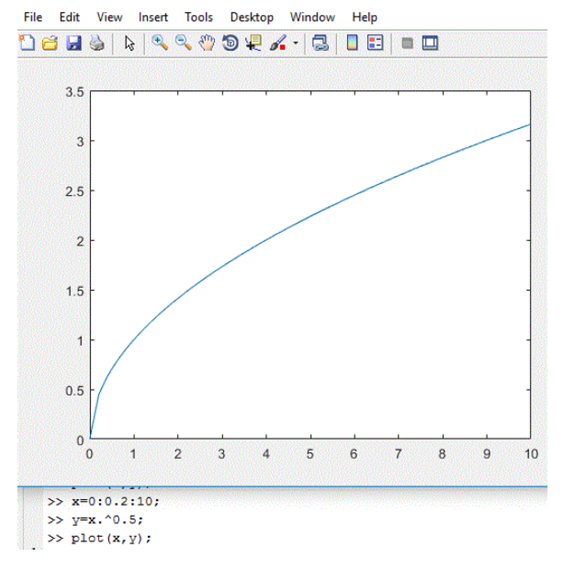 | MATLAB, 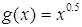 |
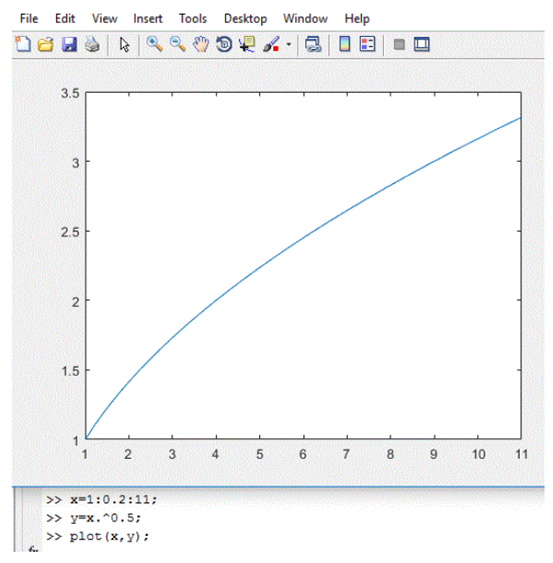 | MATLAB, 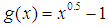 |
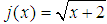 .
.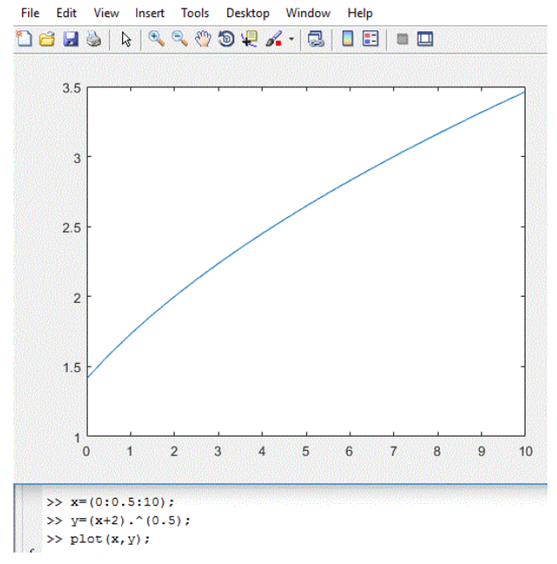 | Figure 4. 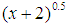 |
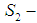 convex is analogous. See: Assume that it is not the case that
convex is analogous. See: Assume that it is not the case that 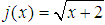 is
is 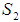 -convex. That means that it is possible to find at least one value for a or b or even for
-convex. That means that it is possible to find at least one value for a or b or even for  or x such that it is not true that
or x such that it is not true that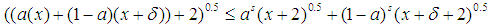 . In this case, we know that (A)
. In this case, we know that (A) 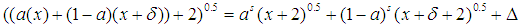 ,
, 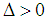 . a can always assume the value 0. If we replace a with 0 in (A), however, we get that
. a can always assume the value 0. If we replace a with 0 in (A), however, we get that 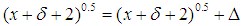 . The last equation implies that
. The last equation implies that 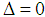 , but this is a contradiction with our assumptions, and therefore proves that our assumptions are equivocated. That leads us to the desired result, since the mistake was assuming that
, but this is a contradiction with our assumptions, and therefore proves that our assumptions are equivocated. That leads us to the desired result, since the mistake was assuming that 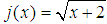 was not part of
was not part of  .
.3. Conclusions
- In this paper, we have provided a very trivial example of
 convex function. In fact, we provided a family of trivial examples of
convex function. In fact, we provided a family of trivial examples of 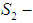 convex functions (change the constant, values above and below 0). That should make Professor Mark Nelson like our
convex functions (change the constant, values above and below 0). That should make Professor Mark Nelson like our 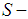 convexity more, but it should also make Hudzik, Maligranda, Dragomir, and a few other professors a bit more upset, since we have proven that one of the theorems of Hudzik, supposed to generate
convexity more, but it should also make Hudzik, Maligranda, Dragomir, and a few other professors a bit more upset, since we have proven that one of the theorems of Hudzik, supposed to generate 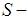 convex functions, cannot really be trusted. We have provided an entire family of trivial counter-examples to it here. Now the definition of
convex functions, cannot really be trusted. We have provided an entire family of trivial counter-examples to it here. Now the definition of 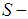 convexity is settled through [4], so that we can write more about examples. Next, we will be analysing the work already done in terms of examples.
convexity is settled through [4], so that we can write more about examples. Next, we will be analysing the work already done in terms of examples.Note
- 1. Supplementary here means '>', not '≥'.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML