1. Introduction

In 1872, the Felix Klein Erlangen Program aimed at the complete classification of geometries through inclusion of the internal symmetry groups.

The studies of Felix Hausdorff, in the forties, and Benoît Mandelbrot, at the IBM Thomas J. Watson Research Center, in the seventies, produced a definition of fractality through a negative statement –inequality of topological and capacity dimensions, in a vast family of self-similar entities existing in all types of geometry. Self-similarity, affinity, or its distortion, as in fat fractals, are characterized by semigroups – a lesser symmetric structure than what is common to all Geometry.

Therefore, fractals survived as counter-examples, without a proper way to be denominated and classed – a consequence of negativity in their definition, and a pillar to experimental approach. A paradox emerged, mainly in Latin universities:

a) the prohibition of fractal teaching in Math department (a manifestation of austerity), synchronous with its use in natural, computational, social sciences, as well as arts and philosophy.

b) chaos and another morphology trends – catastrophes, otherwise designated as singularities (or, by Vladimir I. Arnold, perestroika) – emerged simultaneously in another private institution. Fractals and Gregory Chaitin computational approach to randomness as a Kurt Godel generalized result, emerged at IBM in New York. René Thom theory, and chaos in Henri Poincaré spirit of limitation to determinism came from Paris at the same moment.

See at (Aubin, 2017) the detailed study of David Aubin, a PhD thesis (Princeton University), UMI #9817022. This is how it is organized:

• Abstract

• Table of Content

• Acknowledgments

• I: Introduction

• II: Structures

• III: Catastrophes

• IV: Fundamental Research

• V: Stability

• VI: Qualitative Dynamics, part 1, part 2

• VII: Strange Attractors, part 1, part 2

• VIII: Chaos, part 1, part 2

Where a philosophic standpoint on Lyapounov exponent has not yet been studied. Chaos appears as measure of exponential divergence - positive Lyapounov lambda. Inverting time, lambda is less than zero – no chaos for the past, total determinism. More interesting becomes the common endeavor of ALL classical deterministic systems, prior to Poincaré and Lyapounov – precision for the future, antagonism of ideas and scenarios. The flagrant contradiction of the origins – of the universe, big bang versus Hoyle continuous creation; for life, as local or panspermia; the seat of the soul, as dual in Popper and Eccles, or self-organized, as Von Foerster, Maturana and Varela eloquently sustained; etc. Origins backwards, chaos in future – a cabal symmetry illustrated By Lyapounov exponents.

c) Mystery of origins as necessary, classification of fractals as doable. Subjects for future writings and lectures. More modest today, the denomination of rare differentiable fractals drawn by computation of small variation of quadratic chaos generators.

d) The pictures of Lyapounov exponents, published by Markus, corresponding to symbolic sequences which control a quadratic – or topologically conjugate – iteration, is, through the alternation of parameters A and B, equivalent to a succession of zeros and ones. For such a symbolic sequence, the natural topology is the one of a Cantor set.

Now, it is also true that the infinite ensemble generated by sequencing zero and one is the transcription of the unit interval in basis 2; to what conditions is such a sequence bound to obey, in order to designate a generic real number, instead of a point in a meagre, zero – measure set such as a Cantor set? Are such conditions compatible with the hypothesis basilar to the works of Markus? If so it was, this would be another instantiation of a new paradigm – constructing fractals as number images.

A procedure developed in divergent ways by a few authors:

- Jenny Harrison (1989), through a construction inspired by Denjoy and leading into continued fractals;

- Michel Mendes-France (1991), when he considered number-theoretic properties of sequences of coefficients for trigonometric sums.

-The early departed authors Mario Sarreira and Jose Sousa Ramos (1991) in their codification of cubic Mandelbrot sets.

2. Development

(1) 0,111111... = 1.000...

is the constitutive equation of the binary number system. For a radix b > 2, it will not happen; therefore, the free semigroup generated by the two symbols 0 and 1 shall define a Cantor set (for a global study see (Komornik, 2017).

The inverse inequality (0.1111... > 1.00...) is accomplished for b < 2, where a multiplicity of developments, with a magnitude dependent on the location, is present for each point of the unit segment, thus structuring it as a multifractal.

Equation (1) fills the same role as the just-touching collage giving rise to connected sets. The apparent tridimensionality of the pictures in (1) is a consequence of the difference between the basins of attraction, the cardinality of which is conjectured to be equal to the periodicity in the control signal (the A B sequence).

Such a conjecture would validate the following corollaries:

a) The existence of a shift symmetry in the control sequence, with the same period as it

b) The irrelevance of the first n terms of the control sequence, for whatever n, in periodic A B sequences

c) Modulo the postulate of equivalence between images, generated by points with a multiple definition for basins of traction (depending on the initial terms of control sequence), then the shift symmetry of period P reported in a) becomes, by generalization, a unit-shift symmetry.

From these points we are bound to deduce, for every 01 sequence:

d) Every multiple or sub multiple by a power of 2 is equivalent and

e) Every two sequences diverging in a finite number of transient terms are equivalent

Thus: 0.001001... ≡ 0.010010... ≡ 0.1001001...

f) 0.111001001... = 0.001101001...

This means that for the set of numbers, in the unit interval, expanded in binary system in a periodic way (dyadic rationals), a quotient set is generated through these equivalences.

Are these quotient classes the real numbers, or something alike in a Cantor set?

An answer is suggested by the geometric significance of equation (1): We are dealing with sequences ABBB... and BAAA..., which as the same as (through the exclusion of the first symbol, a transient) every constant sequence (of period one).

Their identity, after (1), simply means that both display the same structure (the haircomb generated by the Cartesian product of the chaotic windows in the parameters of a Feigenbaum bifurcation × the unit interval); the interchange between A/B being displayed as different orientation (horizontal versus vertical).

This is only a part of a more general isomorphism, the one of duality.

It can be expressed in 3 ways:

a) Symbolically, by the replacement of all A’s by B’s and vice-versa (reminiscent of the ambivalence of symbolizing, once quoted by Wittgenstein: It is necessary that P and not- P may designate the same utterance).

b) Geometrically, by transposition: Reflecting along the diagonal of the unit square.

c) Arithmetically, as the symmetry between X and 1-X and the unit interval (dualism) replacing the unit interval by its half.

Illustrating c) by means of an example, we have:

AAABBABAB, or 000110101

= means ≡

BBBAABABA, or 111011010

Which sum is 111111111... =1

Trivial cases: Periods 1, 2, 3

Period 1: AAA... or BBB..., 000... ≡ 111...as above (Feigenbaum ∩ chaotic window X [01])

Period 2: of the 4 possibilities (AA, AB, BA e BB). Two reinstate the period 1 are to by excluded: 00 and 11. The two others, 01 and 10, are identical both by shift and by duality.

Period 3: 000 ≡ 111 are excluded (period 1)

All the other 6 are equivalent:

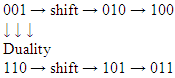Therefore, until now, only one sequence modular above equivalences exists in each period 1, 2, 3. We might name then after their numeric values in binary – 1, 2, 4 corresponding to 1, 10, 100.

From now on everything shall become more complex.

Periods 4 to 7

Period 4: 16 sequences

Are identifiably excluded as they repeat the sequence of period 2.

The excluded sequences correspond to numbers 0,19, 9,10.

As for the other i 2 sequences, we shall do arithmetic in decimal, instead of binary.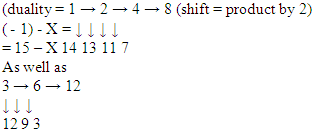

As a convention, we shall designate them as the 8 and 12 sequences, in order to enhance the leading digit 1

8 : 1000

12 : 1100

Period 5:

- Exclusion of 00000 and 11111

- No repeating of sub multiple sub sequences as 5 is a prime number

- Generation of their respective sequences

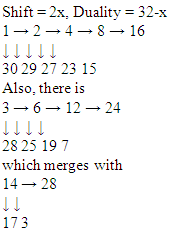In fact, the numbers subsuming them (24,17) represent the same pattern, adjusted from a shift:

24 : 11000

17 : 10001

The same phenomenon occurs between

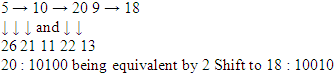Therefore, we shall select, as tokens for periods sequences:

16 : 10000

17 : 10001

18 : 10010

Period 6: 64 sequences; elimination of 0 and 1, as usual

6 being a multiple of 2 and 3, we are bound to eliminate repetitions of segments 10 and 100, live

101010 : 42

100100 : 36

But it proves better to start by their duals.

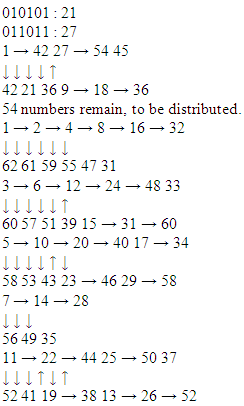Therefore the sequences will be codified as:

32: 100000

33: 100001

34: 100010 (or 56 = 111000)

35: 100011

36: 100101

Period 7: Excluding 0 and 1, and there being no submultiples, we need to explore 126 numbers

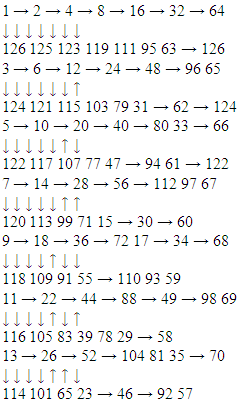15 and 17 are not suitable generators, as previously they were found. We might remark that these sequences always have 14 elements; therefore, we need 2 more (7 + 2 = 9, 9 x 14 = 126). The last elements in the 1st line grow according to arithmetic progression (647,70). 71 is present in one previous sequence, as is 72. So, 73 and 74 should be good generators.

Until now, we have the followings symbolic sequences:

Periods

1, 2, 3

4 5 6 7

1 (= 1 8 (=1000 16-10000 32 64

2 (= 10 9 (= 1001 17-10001 33 65

4 (= 100 18-10010 34 66

35 67

37 68

69

70

73

74

Generalization

If p is a prime number, this having no sub-multiples, the only excluded sequences are 0 and 2p – 1 (0000... and 1111...). Therefore, if every single set of isomorphic numbers (in terms of duality + shift) has the same quantity of terms, as they did until now, their quality must depend on the factorization of 2p – 2 = 2(2p – 1). Let us try it for the next prime numbers: 11, 13, 17. 11: 211 = 2048; 211 – 2 = 2046 = 2 x 1023 = 6 x 341 = 6 x 31 x 11 = 11 x 186 = 22 x 93

Therefore, there should be 93 ensembles of 22 equivalent numbers.

13: 213 – 2 = 8190 = 10 x 819 = 13 x 10 x 63 = 26 x 315

315 equivalent segments

17: (2 (17-1)-1) being divisible by 17, this quotient should be the member of different sequences. For composite numbers, the problem is more difficult, we should eliminate the instantiation of sub-multiples. For instance, in the period 8 (28 = 256) we eliminate:

- 0 and 255

- The translates of period 2 (10101010 and 01010101)

- The duals and translate of 8 and 9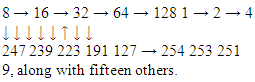

Therefore, 256 – 2 – 2 – 16 – 16 = 220 will remain, to be distributed through 16 – long ensembles.

3. Conclusions

The number of image-generations sequences grows with N in a was majorated by ( 2(p -1) – 1)/p, for prime p; which means, exponentially in N. Therefore, it is not a denumerable set. Is it a continuation, or a Cantor set, or something in between (a fat Cantor set)?

As a tentative answer, let us be inspired by the following:

- A number such as 0.897897897... in decimal radix expansion is = 897.0.001001001... = 897/999

Therefore, in fractal number system, the corresponding numbers are to be

1 / 1, 2 / 3, 4 / 7, 8 / 19, 9 / 15 = 3 / 5

16 / 31, 17 / 31, 18 / 31, 32 / 63, 33 / 63 = 11 / 21

34 / 63, 35 / 63, 37 / 63, 64 / 127, 65 / 127, 66 / 127, 67 / 127, 68 / 127, 69 / 127, 70 / 127, 73 / 127, 74 /

127

How for did such a sequence fil the [0 1] interval? Is it fat or meagre? What about its

Hausdorff dimension? Sequences, essentially because shift symmetric fails (it was a consequence of periodicity); therefore applet tridimensionality (multimodality) is lost.

However, duality, as well as irrelevance of transients, are maintained.

We might understand for the above that, restrictions of the a periodic, being less severe, on stating hypothesis – Markus pictures as images for numbers – which was not refuted in the realm of dyadic rationals, keeps maintaining the pertinence of a brand-new conjecture.

If p is a prime number, this having no sub-multiples, the only excluded sequences are 0 and 2p – 1 (0000... and 1111...). Therefore, if every single set of isomorphic numbers (in terms of duality + shift) has the same quantity of terms, as they did until now, their quality must depend on the factorization of 2p – 2 = 2(2p – 1). Let us try it for the next prime numbers: 11, 13, 17. 11: 211 = 2048; 211 – 2 = 2046 = 2 x 1023 = 6 x 341 = 6 x 31 x 11 = 11 x 186 = 22 x 93

Therefore, there should be 93 ensembles of 22 equivalent numbers.

13: 213 – 2 = 8190 = 10 x 819 = 13 x 10 x 63 = 26 x 315

315 equivalent segments

17: (2 (17-1)-1) being divisible by 17, this quotient should be the member of different sequences. For composite numbers, the problem is more difficult, we should eliminate the instantiation of sub-multiples. For instance, in the period 8 (28 = 256) we eliminate:

- 0 and 255

- The translates of period 2 (10101010 and 01010101)

- The duals and translate of 8 and 9

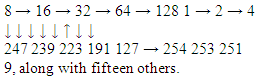Therefore, 256 – 2 – 2 – 16 – 16 = 220 will remain, to be distributed through 16 – long ensembles.

ACKNOWLEDGEMENTS

We would like to extensively thank the fellows from the editorial board of the MIJPAM, whose services were priceless, including, amongst those, editing this article, and sponsoring its publication. Our research has been funded by Emma in the framework of the EU Erasmus Mundus Action 2.