Maria Ribeiro
UNESA
Correspondence to: Maria Ribeiro, UNESA.
| Email: |  |
Copyright © 2017 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
In this note, we study a possible proof of the Four-colour Theorem, which is the proof contained in (Potapov, 2016), since it is claimed that they prove the equivalent for three colours, and if you can colour a map with three colours, then you can colour it with four, like three starts being the new minimum. We get to prove that this interesting proof, made of terms such as NP-complete, 3-SAT, certificate, hardness, satisfiable, and certifier is at most an attempt to have a proof, and an exotic one, since all that is involved is very different from what we expect to see in a proof of this type.
Keywords:
Four-colour, Theorem, Proof, Map
Cite this paper: Maria Ribeiro, A Short Note on a Possible Proof of the Four-colour Theorem, Modern International Journal of Pure and Applied Mathematics, Vol. 1 No. 1, 2017, pp. 12-18. doi: 10.5923/j.mijpam.20170101.03.
1. Introduction
(Numberphile, 2017) is a nice introduction to the problem we want to talk about in this piece: The Four Colour Theorem.In an informal document, we find the theorem stated in the following manner (Thomas, 1995):The Four Color Problem dates back to 1852 when Francis Guthrie, while trying to color the map of counties of England noticed that four colors sufficed. He asked his brother Frederick if it was true that any map can be colored using four colors in such a way that adjacent regions (i.e. those sharing a common boundary segment, not just a point) receive different colors. Frederick Guthrie then communicated the conjecture to DeMorgan. Some countries do not appear in a continuous manner in the world map. For instance, The Maldives belonged to England (Infoplease, 2017) at a certain stage, but this island is close to Africa, to the right side, in the world map. See (red balloon, bottom, right whilst England is top, left):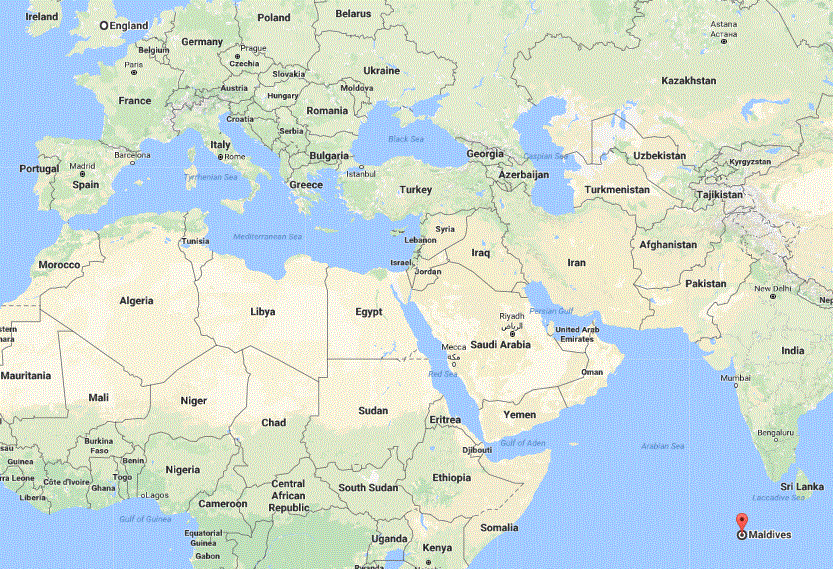 | Figure 1 (Google, 2017) |
Because of that, it is possible to present an image like the one we see below this paragraph, and still claim that we are dealing with a planar map representing countries and their geometric relationship.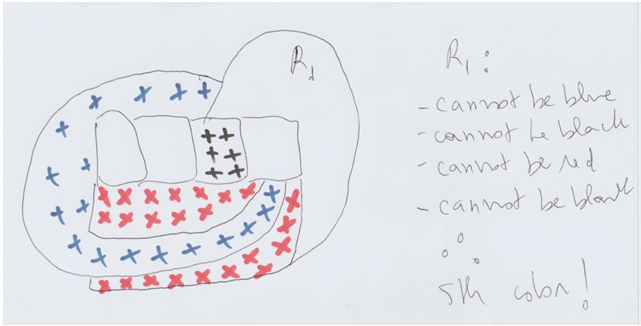 | Figure 2 (Pinheiro, 2017) |
The Four-Colour Theorem is stated in different ways in different sources. One version of the theorem will allow for exclaves, for instance. The other version will not allow for that.From (West, 2008):The four colour theorem (also known as the four colour map theorem) states that given any plane separated into regions, such as a political map of the states of a Country, the regions may be coloured using no more than four colours in such a way that no two adjacent regions receive the same colour. Two regions are called adjacent only if they share a border segment, not just a point. Each region must be contiguous: That is, it may not have exclaves like some real countries such as Angola, Azerbaijan, the United States, or Russia.(American, 2016) lets us learn the meaning of Exclave:A part of a Country that is isolated from the main part and is surrounded by foreign territory.When you click on Angola, which is underlined in the original text of the quotation, you get the following map for it: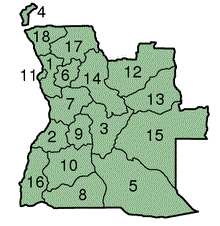 | Figure 3 (American, 2016) |
We then assume that our exclave would be the piece of land with the number 4 next to it. That is important because, with this definition settled, our counter-example, from Figure 2, is not a counter-example anymore, since we do have exclaves there. The problem then becomes the sigmatoid contiguous. See what Bartlett (2014) teaches us:Theorem. (Kempe, 1879) Take any map, which for our purposes is a way to partition the plane R2 into a collection of connected regions R1, . . . Rn with continuous boundaries. There is some way to assign each region Ri to a colour in the set {R, G, B, Y}, such that if two regions Ri, Rj are touching (i.e. they share some nonzero length of boundary between them,) then those two regions must receive different colours.The boundaries of our counter-example (Figure 2) are definitely not continuous. The region that has discontinuous boundary (red) is disconnected. See (Muhammad, 2017):A graph that is in one piece is said to be connected, whereas one which splits into several pieces is disconnected.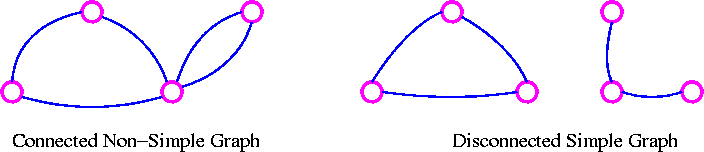 | Figure 4 |
A graph G is connected if there is a path in G between any given pair of vertices, otherwise it is disconnected. Every disconnected graph can be split up into a number of connected subgraphs, called components.If we think of places that are connected to each other via a border that is part of the own place, so say the end of a golf course, it seems that to need two colours we need two countries that touch each other, to need three colours we need three countries that touch each other, and so on. Each time one of the countries does not touch one of the others, it may acquire the colour of the Country that it does not touch, so that we have fewer colours than countries. In this way, we get five if we have five countries and each one touches all the others. That does not seem to be possible if the own Country has to be part of its boundary, like a single solid mass, since we would end up isolating one as we get to the Country number four, and we therefore could repeat the colour of the isolated Country in the fifth Country. Notwithstanding, if our border is something different, so say water, that may be possible. None of the definitions of the four-colour theorem problem mentions that we cannot have bridges, and that would certainly impose too many restrictions over a map that is supposed to display our usual countries. Certain things that exist to connect one Country to another do not appear in what we are used to call planar maps: For instance, bridges and underground tunnels. Yet, a bridge that connects one Country to another could contain the boundary between one Country and another. In this case, we do have an easy counter-example. See: | Figure 5 |
In the middle of these five countries there is something that we call border, so that it may be a lake, for instance, a lake that belongs to all of them or to none of them, as the ocean goes. We determined that some miles belong to the Country and others belong to nobody. With this, all the four in the shape of ball connect to each other, like the lake would be enough. They then should have different colours, one for each. The fifth Country appears around them all and therefore has direct contact with them all, so that it cannot have any of the four colours that have already been used. We now have our fifth colour: Needed and used. In fact, we have a tripoint border between Paraguay, Brazil, and Argentina, as you can see in the picture below: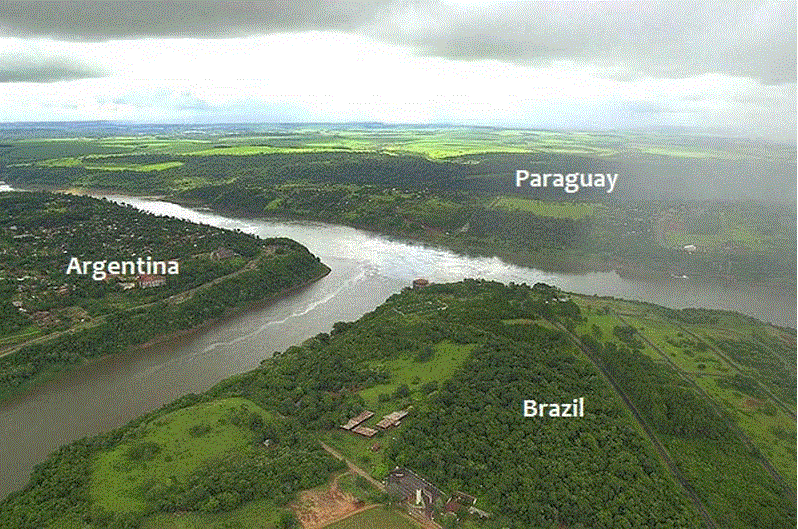 | Figure 6 (Twisted Sifter, 2012) |
And, if you think that one of the countries in the previous drawing is not contiguous (white), we may choose to have five circles instead. Like this: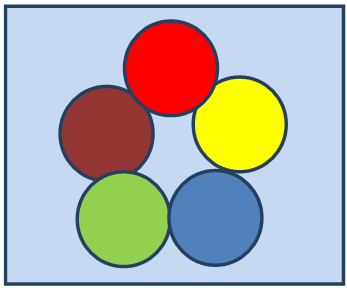 | Figure 7 |
2. Conclusions So Far
We initially had a counter-example to a certain version of the four-colour theorem, which was not the most popular inside of Mathematics. That was not a counter-example to the popular version because it had at least one disconnected region.We then worked a bit more and came up with a counter-example to the popular version of the theorem, since we now did not have disconnected regions. We first observed that we would need the countries to appear in the same number as the colours or in superior number to prove that five or more colours were needed instead of four as a minimum. We also noticed that all countries would have to make border with each one of the others if we had five and we wanted to guarantee that five colours were the minimum amount needed. This because if any Country did not have contact with any other, we could use the colour of that one that had no contact with it again, and therefore we would have less than five colours. We noticed that it was not possible to have contiguous countries that connected through their own territory if those were always continuous lands made of solid matter close to the border because by the time the fourth Country were added, one Country would become isolated and we could then repeat its colour. What was needed was something like water in between, perhaps bridges and things like that. We then found even a real-life example to bring us inspiration. That was the border between Paraguay, Brazil, and Argentina. Because of all our conclusions, the reasoning presented in (Gonthier, 2008) does contain some flaw. It is frequently the case that proofs initially taken to be sound are proven to be unsound in Mathematics. The book (Pinheiro, 2016) brings more evidence on that.(Ribeiro, 2017) brings the fallacy involved in the proof from (Gonthier, 2008).We then conclude that if there is any hope for this theorem, it should be in the version that would be called five-colour theorem, not in this version we studied here.The image we have presented is actually very likely to appear in a map exactly in the way it is displayed here (so that the argument involving naturalness, which is commonly used to discard possible solutions, would not produce an effect here), so that, as a consequence, the theorem is not verified either in the intuitive version (where disconnected regions are allowed) or in the non-intuitive version (mathematical version, where disconnected regions are not allowed). With this, what happens? Any applied version of the problem should always be wrong: We should always be able to find a counter-example. If we transfer the problem to pure mathematics, however, and we then talk about sets of polygons being coloured, it should be true, as we here explained.We are now going to criticize the proof presented in (Potapov, 2016).
3. Against Potapov
See this extract, taken from (Potapov, 2016): | Figure 8 |
Here we have our main problem: An edge is formed of two nodes, quite trivially. The author seems to call these nodes u and v. He then says that we assign colours to the nodes themselves. The issue is that each node will belong to a few countries in a map, is it not? And that is actually the main thing about the four-colour theorem. To solve the problem that is, in principle, solved by the theorem, we must colour each adjacent country of a colour that is different from the colour of the main Country we observe. Oh, well, a node will be part of a few countries. These countries cannot ever have the same colour, since they will be adjacent to each other. How can you then have a single-coloured node? We think we need to say nothing else: This is obviously NOT a proof of the four or three colouring theorem. This is at most an error, and a very evident one. | Figure 9 |
Naming the nodes forming the edges of the triangles true, false and base is unnecessary and creates a lot of confusion (Pinheiro, 2015), since it seems that we mean something with this assignment. In principle, however, we are simply naming these nodes. We can give them any name, so that a, b, and c would look and sound more reasonable. We then say triangle with common Base and this base is with a capital b. In this case, he must be referring to the node he called Base. The node is called Base, but base reminds us of triangle and we then think of an edge. We then say two nodes v with index i and v with index i bar connected in a triangle with common Base. What does he mean by common Base here is also an issue: If it is just one triangle, what is meant by common? If it is trivial, then it is not making much sense. Gets the same colour as True, but, once more, True is a node and could not have a particular colour, for that would destroy any chance that we can solve the problem. If the node has a particular colour, then all the countries that use that node as a vertex will have that colour, quite trivially. That destroys any chance that we can prove the theorem, since it is trivially impossible to colour those adjacent countries with different colours. We clearly don’t need to say anything else: This is not a proof. This is at most entertainment.
4. Final Conclusions
We have here nullified one more proof of the Four-Colour Theorem, the proof presented in (Potapov, 2016).The main issue with the possible proof is that the author talks about colouring nodes, that is, vertices, but those are part of the border of the Country, and, if we colour those, the colour would have to be set also for the adjacent countries, and those would then have to have the same colour as the first one, and therefore there would be borders that are formed of countries that have the same colour, but that means that the conditions of the theorem are not being respected, the most basic ones. If the most basic conditions of the theorem are not being respected, we clearly DO NOT have a proof for it in this reasoning.Other problems were identified: For instance, there is reference to a common base with capital b, but that is the name of an edge of a triangle for the author of the possible proof. He then says that two of his nodes will have a common Base, but what he probably meant is that these two vertices will form the edge. He also calls the other nodes of the triangle true and false, but that creates enormous confusion, since, according to his explanation, these names should simply be random assignments. We get confused and start thinking of Classical Logic and other things. That comes on the way to understanding the actual reasoning behind the possible proof. With this, we now have nullified the proofs of the Four-Colour Theorem belonging to G. Gonthier (2008), Kempe (1879), in case Gonthier correctly refers to his work (Gonthier, n.d.), and Potapov or whoever is being mentioned by him on (Potapov, 2016) in a non-explicit manner. We do believe that the Four-Colour Theorem can be true in the purely mathematical context, that is, with no mention to maps or anything that be not completely abstract. It is just not true in the case of actual maps: The right words being used there (Pinheiro, 2015), and we should have a nice mathematical theorem, from Pure Mathematics, not applied.
References
| • | Potapov, I. (2016). 3-Coloring is NP-Complete. Retrieved May 4, 2017, from http://cgi.csc.liv.ac.uk/~igor/COMP309/3CP.pdf |
| • | Numberphile. (2017). The Four Color Map Theorem - Numberphile. Retrieved March 22, 2017, from https://www.youtube.com/watch?v=NgbK43jB4rQ |
| • | Thomas, R. (1995). The Four Color Theorem. Retrieved March 22, 2017, from http://people.math.gatech.edu/~thomas/FC/fourcolor.html#Why |
| • | Infoplease. (2017). Maldives. Retrieved March 22, 2017, from http://www.infoplease.com/Country/maldives.html |
| • | Google. (2017). Maldives. Retrieved March 22, 2017, from https://0x9.me/FyIQ6 |
| • | Pinheiro, M. R. (2017). Four-Colour Theorem. Retrieved June 2, 2017, from http://mathematicalcircle.blogspot.com.au/2017/03/four-colour-theorem.html |
| • | West, B. (2008). Four Colour Theorem. Retrieved March 22, 2017, from https://www.cs.mcgill.ca/~rwest/link-suggestion/wpcd_2008-09_augmented/wp/f/Four_color_theorem.htm |
| • | American Heritage. (2016). Exclave. Retrieved March 22, 2017, from http://www.thefreedictionary.com/exclave |
| • | Bartlett, P. (2014). Math 7H: Honors Seminar. Retrieved March 22, 2017, from http://web.math.ucsb.edu/~padraic/ucsb_2014_15/math_honors_f2014/math_honors_f2014_lecture4.pdf |
| • | Kempe, A. B. (1879). On the geographical problem of the four colours. American Journal of Mathematics 2 (part 3), 193–200. |
| • | Muhammad, R. B. (2017). Definitions and Examples. Retrieved March 22, 2017, from http://www.personal.kent.edu/~rmuhamma/GraphTheory/MyGraphTheory/defEx.htm |
| • | Twisted Sifter. (2012). Where Three Countries Meet: Famous Tripoints Around the World. Retrieved May 2, 2017, from http://twistedsifter.com/2012/05/famous-tripoints-around-the-world/ |
| • | Gonthier, G. (2008). Formal Proof - The Four-Colour Theorem. Notices of the AMS, 55(11), 1382–1393. Retrieved from http://www.ams.org/notices/200811/tx081101382p.pdf |
| • | Pinheiro, M. R. (2016). Funny Thinking in the 21st Century: Truth or Dare? CreateSpace. Retrieved from https://www.amazon.com/Funny-Thinking-21st-Century-Truth/dp/1541301935/ref=asap_bc?ie=UTF8 |
| • | Ribeiro, M. (2017). The Four Colour Theorem: Mistakes and Innacuracies, Possible Proofs. Modern International Journal of Pure and Applied Mathematics, 1(1), 5–11. Retrieved from http://www.sapub.org/journal/articles.aspx?journalid=1143 |
| • | Pinheiro, M. R. (2015). Words for Science. Indian Journal of Applied Research, 5(5), 19–22. Retrieved from https://www.worldwidejournals.com/ijar/articles.php?val=NjQ0MQ==&b1=853&k=214 |
| • | Gonthier, G. (n.d.). A Computer-Checked Proof of the Four Colour Theorem. Retrieved April 5, 2017, from http://www2.tcs.ifi.lmu.de/~abel/lehre/WS07-08/CAFR/4colproof.pdf |











 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML