1. Introduction

(Numberphile, 2017) is a nice introduction to the problem we want to talk about in this piece: The Four Colour Theorem.

See what Bartlett (2014) teaches us:

Theorem. (Kempe, 1879) Take any map, which for our purposes is a way to partition the plane R² into a collection of connected regions R₁, . . . R_n with continuous boundaries. There is some way to assign each region R_i to a colour in the set {R, G, B, Y}, such that if two regions R_i, R_j are touching (i.e. they share some nonzero length of boundary between them) then those two regions must receive different colours.

From (Muhammad, 2017), we read:

A graph that is in one piece is said to be connected, whereas one which splits into several pieces is disconnected.

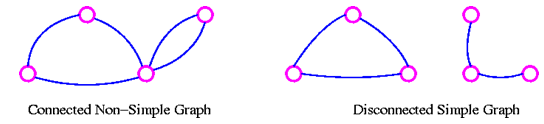A graph G is connected if there is a path in G between any given pair of vertices, otherwise it is disconnected. Every disconnected graph can be split up into a number of connected subgraphs, called components.

Researcher Gonthier came up with a proof that he judged final for this theorem (Gonthier, 2008). Dr. Pinheiro then found a counter-example, like for this theorem, as you can see on (Pinheiro, 2017). With this, we were sure that his proof had some flaw.

Upon investigating it deeper, we found one of this flaws. He seems to have inherited it from Kempe.

In this paper, we intend to talk about this little finding: If we can prove that it is an actual flaw, Gonthier’s proof will be deemed unsound, and we will then come back to not having any proof for the theorem. It is just that, this time, we also have a counter-example that really looks OK. If nobody presents sound opposition to Dr. Pinheiro’s counter-example, we know that the theorem is not true, and therefore we know that no sound proof for it can exist. In this case, all those claiming to have proofs for this theorem would have to have committed a mistake somewhere in their mathematical developments.

2. Development

From Dr. Pinheiro’s website (Pinheiro, 2017a), with adaptations:

This is actually about a paper that is cited in the paper Formal Proof (Gonthier, 2008).

Here we should find out more about reducibility according to the author (Gonthier, n.d.):

Open line segment seems to then be a concept that closely relates to open real interval, is it not? Basically, if we understood it well, we take away the vertices and it becomes open, like before, with the vertices, it was a closed line segment. This is what they are calling edges, they here say.

The basic problem that we have with what has been said so far is the fact that they seem to redefine a really old concept from Mathematics and, later on, use Euler’s theorem, which was created for the old concept, in the way it used to be: You would first have to prove that the new edge does the same trick. Is our school of Mathematics too old or that still makes sense, please?

The set of nodes contains the endpoints of the edges, so that nodes are not nodes either: They are the endpoints of the edges.

If the regions are now called faces, we immediately come up with a doubt: Is the ocean, which surely appears in maps, also a face?

We don’t know, but we are thinking that the sea could easily be seen as a connected component of the complement of a polygonal outline. Are we pushing it?

Could it be a supplement?

Can we mention (Pinheiro, 2015) again?

The extract below came from (Gonthier, n.d.).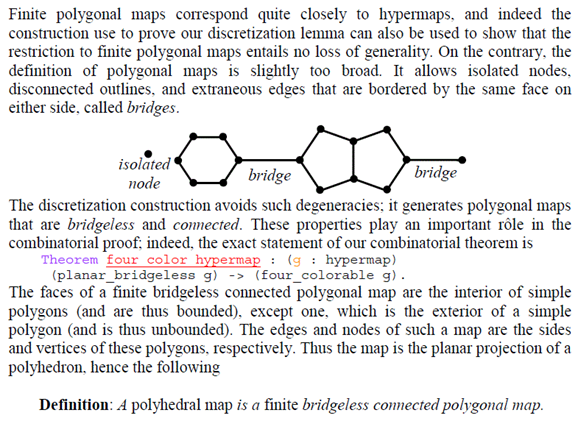

A face that is the exterior of a simple polygon and therefore is unbounded is something that puzzles us: An unbounded face of a polygon? Wouldn’t face imply boundaries? Do we have an example of face without boundaries before our author comes up with this one, please?

Tom Cruise has an interesting sound track/YouTube for this one: (The Tonight, 2015). He says: I can’t feel my face when I am with you, but I love it, but I love it…

Once more, for the map to be the planar projection of a polyhedron, the ocean would have to be the same as a Country. Would that not be something unwanted in terms of mathematical calculations?

We think that the absence of respect for the already existing mathematical definitions and the excess of creativity allied to the absence of care when creating new concepts is a bit annoying.

The absence of necessity is what kills all: Why not simply using the terms we already have and know so well? Edge is the open line segment. Vertex is the new node.

It is nice creating new things, but perhaps painting a canvas pays more in this case. Once more, we don’t want to increase the amount of confusion in Science: We realistically are confused enough with what is already around.

Face should be something limited by edges, in our humblest. Vertex should be where two edges meet.

In this way, we can use Euler’s Theorem with no fear: We all have the same vocabulary.

Master Angela, in discussion with us about The Monty Hall Problem (Pinheiro, 2016), mentioned this in a very interesting way: We must have common grounds…

It is possible that the author needs to refer to the endpoint of the edge for some reason, but that is our vertex, is it not? So far we never needed to detach anything from the edge in order to talk about the endpoint, our vertex. We are really not seeing any necessity of creating any of this. Perhaps if we needed to refer to the part of the vertex that comes from a particular edge, if that makes sense, we would need this concept, like if referring to that really were a necessity. We are really not seeing this necessity here.

Euler’s Formula is well written in (Fiedorowicz, 2017):

So, Euler has referred to the fellow’s nodes in another way: Vertices. Why not copying him, we wonder?

Now, he says that Kempe committed a mistake that nullified his proof. See (Gonthier, n.d.):

Three edges meet on each node or three edges meet on each vertex could be expressed in symbols as 3E = V, is it not? Since the fellow replaces V with N in his formula, we would have 3E = N. Why we would choose 3V = 2E instead is a mystery to us, but, if we can choose one or another, then we need to study at least both options in what they want to say is a proof, no doubts about it. Worth making a remark here: In one option, a vertex is worth 2/3 of an edge, that is, not even one full edge. In the other, the vertex is promoted to 3 times the value of the edge. That is really really contrasting. We don’t know, but even in Computer Science that should make an extraordinary difference, is it not?

See all the action in the pictures below (Gonthier, n.d.):

If we were dealing only with one polygon we could perhaps justify choosing the first relationship that we see right above this paragraph.

As another point, however, we should be talking about proportions when we establish mathematical relationships between variables in this case. We do understand that, in the last case, 3 edges return a vertex, but, to be sincere, it suffices that we choose edges in a special way and we won’t have a vertex, like we can definitely get three edges without us being able to determine a particular vertex (perhaps two of them will determine one vertex and the other will determine another). If it is not any edge that can be selected for us to get one vertex, our relationship should not be of the proportional type, and we therefore cannot use the rule we say we have used. The same problem seems to occur in the alternative situation. It is all mathematical nonsense therefore.

Let’s not hang on to this one, since the author himself says Kempe did commit a bad mistake in this development.

Let’s read his own development instead (Gonthier, n.d.):

You can see that, on the number II, the authors mention b, e, h, and i. On the number I, they mention g.

All the items we mention are necessary for us to claim to have reducibility and unavoidability according to the author.

If we prove that one of these items is unsound, we don’t have reducibility and unavoidability anymore.

The extracts we see below are again from (Gonthier, n.d.).

We have proven here that b contains a very serious mistake, unavoidability is not sound, and therefore the claimed proof is also unsound (based on reducibility AND unavoidability). We can stop by here: Mission accomplished.

3. Conclusions

Gonthier (2008 and n.d.) let us know that

In this case, all the proofs that Gonthier has seen are based on the premise that says that all edges are worth the same and therefore we can apply proportions reasoning to the drawing we see below (Gonthier, n.d.):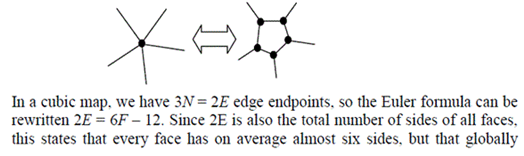

Notwithstanding, Dr. Pinheiro finds arguments that makes us understand that we could not have applied proportions reasoning to the drawing we have just presented. See ((Pinheiro, 2017a), with adaptations):

Three edges meet on each node or three edges meet on each vertex could also be expressed in symbols as 3E = V, is it not? Since the fellow replaces V with N in his formula, we would have 3E = N. Why we would choose 3V = 2E instead is a mystery to us, but, if we can choose one or another, then we need to study at least both options in what they want to say is a proof, no doubts about it. Worth making a remark here: In one option, a vertex is worth 2/3 of an edge, that is, not even one full edge. In the other, the vertex is promoted to 3 times the value of the edge. That is really really contrasting. We don’t know, but even in Computer Science that should make an extraordinary difference, is it not?

As another point, we should be talking about proportions when we establish mathematical relationships between variables in this case. We do understand that 3 edges return a vertex, but, to be sincere, it suffices that we choose edges in a special way and we won’t have a vertex, like we can definitely get three edges without us being able to determine a particular vertex (perhaps two of them will determine one vertex and the other will determine another). If it is not any edge that can be selected for us to get one vertex, our relationship should not be of the proportional type, and we therefore cannot use the rule we say we have used. The same problem seems to occur in the alternative situation. It is all mathematical nonsense.

In this case, all proofs known by Gonthier are actually invalid, since they are all based on the items above.

We then conclude by saying that we never had a single actual proof of the Four-Colour Theorem. Therefore, Dr. Pinheiro’s counter-example, which appears in the paper (Pinheiro, 2017), must be an actual counter-example and, if anything, we should start talking about the Five-Colour Theorem, since the Four-Colour one has been proven to be unsound.