Areo A. O.1, Akinpelu F. O.1, Adetunde I. A.2
1Ladoke Akintola University of Technology, Department of Pure and Applied Mathematics, Ogbomoso, Oyo State, Nigeria
2Prof I. A. Adetunde Consults, 8 Westmount Close, Collyhurst Street, Manchester, UK
Correspondence to: Adetunde I. A., Prof I. A. Adetunde Consults, 8 Westmount Close, Collyhurst Street, Manchester, UK.
| Email: |  |
Copyright © 2021 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
This article investigates MHD effects on porosity and concentration in an unsteady flow in a vertical channel. The nonlinear governing equations of motion with concentration equation incorporate variable porosity were employed and solved analytically using a perturbation technique. The effects of the flow were determined through the physical parameters; Womersley parameter (AI), Eckert number (Ec), Reynolds number (Re), Prandlt number (Pr), Grashof number (Gr), Schmidt number (Sc), Chemical reaction parameter (K1), and the Mass Grashof number (Gc), were investigated on the temperature, velocity and concentration. Graphical results are presented and discussed quantitatively. From the course of the investigation, it was revealed that fluid temperature increase within the channel with increase porosity.
Keywords:
MHD, Porosity, Concentration, Physical Parameters, Vertical Channel
Cite this paper: Areo A. O., Akinpelu F. O., Adetunde I. A., MHD Effects on Porosity and Concentration in an Unsteady Flow in a Vertical Channel, International Journal of Mechanics and Applications, Vol. 10 No. 2, 2021, pp. 30-50. doi: 10.5923/j.mechanics.20211002.02.
1. Introduction
The study of flow and heat transfer in a porous media has also received much attention in the last few decades due to its ever-increasing applications in industries and in contemporary technology. Phenomena of transport in porous media are encountered in many Engineering disciplines. Convective flow through porous medium has applications in the field of Chemical Engineering for filtration and purification processes. In Petroleum Technology, it is used to study the movement of natural gas, oil and water through oil channels or reservoirs. Agricultural Engineering deals with the movement of water and studies in the root zone in the soil. Reservoir engineers deals with the flow of oil, water and gas in petroleum reservoirs. Many researchers have worked on MHD flows, notably among them are Mhone and Makinde [5] have studied unsteady MHD flow with heat transfer in a diverging channel. Ahammad and Mollah [1] studied the MHD free convection flow and mass transfer problem over a stretching sheet considering Dufour and Soret effects with magnetic field. Hazarika and Jadav [4] worked on effects of variable viscosity and thermal conductivity on MHD free convective flow along a vertical porous plate with viscous dissipation. Seddeek and Salama [7] carried out the effects of temperature dependent viscosity and thermal conductivity with variable suction on unsteady MHD convective heat transfer past a vertical moving porous plate. Chakraborty [3] studied MHD flow and heat transfer of a dusty viscoelastic stratified fluid down an inclined channel in porous medium under variable viscosity. Soundalgekar et al [8] discussed MHD effects on impulsively started vertical infinite plate with variable temperature in the presence of transverse magnetic field. Taneja and Jain [9] looked at the unsteady MHD flow in a porous medium in the presence of radiative heat where they obtained expressions for velocity, temperature and rate of heat transfer. Attia [2] have investigated an unsteady MHD couette flow and heat transfer of dust fluid with variable physical properties.Several studies involving heat and mass transfer in Newtonian fluid flows through porous media have been undertaken. However, the combine effects of porosity and viscosity with viscous dissipation have not been incorporated. This work is set out to investigate the effect of porosity and viscosity on unsteady flow of MHD with viscous dissipation and concentration in a porous vertical channel.
2. Mathematical Formulation
The effect of a uniform transverse magnetic field B on unsteady two-dimensional electric conducting fluid flows are considered and its velocities are given as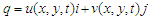
 (a)through a symmetric vertical channel (
(a)through a symmetric vertical channel (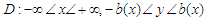 ) where (
) where (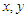 ) are Cartesian co-ordinates such that
) are Cartesian co-ordinates such that 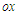 is the axis of symmetry of the channel and
is the axis of symmetry of the channel and 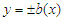 are the rigid and impermeable walls of the channel. The walls of the channel are kept at a constant temperature
are the rigid and impermeable walls of the channel. The walls of the channel are kept at a constant temperature 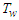 . The fluid is incompressible with uniform properties i.e. density
. The fluid is incompressible with uniform properties i.e. density 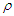 , kinematic viscosity
, kinematic viscosity 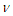 and electrical conductivity
and electrical conductivity 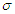 . A volume flux with oscillating frequency
. A volume flux with oscillating frequency 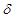 and pulse m is prescribed as in figure 1 below:
and pulse m is prescribed as in figure 1 below: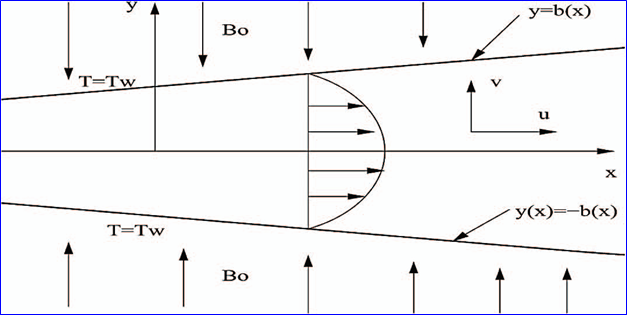 | Figure 1. Problem Geometry (Source Mhone and Makinde, 2006) |
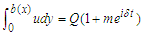
 (b)A uniform magnetic force is applied in the
(b)A uniform magnetic force is applied in the 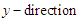 . A very small magnetic Reynolds number is assumed and therefore the induced magnetic field is neglected. Two key physical effects occur when the fluid moves into the magnetic field; the first one is that an electric field E is induced in the flow. There is no excess charge density and then
. A very small magnetic Reynolds number is assumed and therefore the induced magnetic field is neglected. Two key physical effects occur when the fluid moves into the magnetic field; the first one is that an electric field E is induced in the flow. There is no excess charge density and then 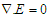 . Neglecting the induced magnetic field implies that
. Neglecting the induced magnetic field implies that 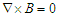 and therefore the induced electric field is negligible. The second key effect is dynamical i.e. a Lorentz force
and therefore the induced electric field is negligible. The second key effect is dynamical i.e. a Lorentz force 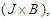 where J is the current density acts on the fluid and modifies its motion. Therefore, there is a transfer of energy
where J is the current density acts on the fluid and modifies its motion. Therefore, there is a transfer of energy 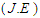 from the electromagnetic field to the fluid. In this study, relativistic effects are neglected, and J is given by Ohm’s law:
from the electromagnetic field to the fluid. In this study, relativistic effects are neglected, and J is given by Ohm’s law: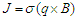
 (c)Within the framework of these assumptions the magneto-hydrodynamic flow relevant to the problem is governed by the set of equations.
(c)Within the framework of these assumptions the magneto-hydrodynamic flow relevant to the problem is governed by the set of equations.
3. Mathematical Analysis
The governing equations for motion under the auspices of the Continuity equation, Momentum equation, Energy equation and Concentration equation are considered, following Hazarika and Jadov [4] and Mhone and Makinde [5] resulted into the following equations; | (1) |
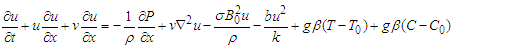 | (2) |
 | (3) |
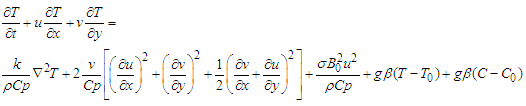 | (4) |
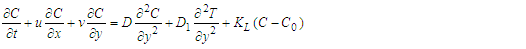 | (5) |
With the following conditions: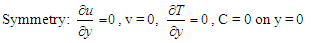 | (6) |
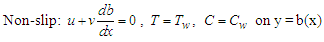 | (7) |
It is convenient to introduce the stream function 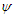 defined by
defined by 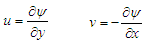 | (8) |
So that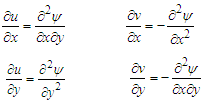 | (9) |
Substituting equation (9) into (1) gives | (10) |
But 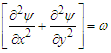 Which can be written as
Which can be written as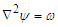 | (11) |
To eliminate the pressure term from (2) and (3), differentiate (2) with respect to 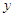 and (3) with respect to
and (3) with respect to 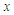 gives
gives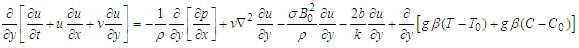 | (12a) |
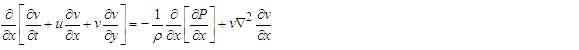 | (12b) |
Subtract equation (12b) from (12a) to give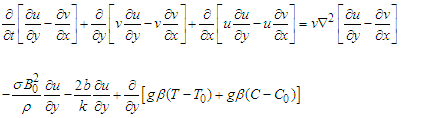 | (13) |
Substituting (9) into (13) yields 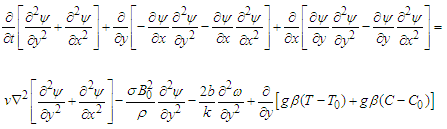 | (14) |
Simplifying (14) further to obtain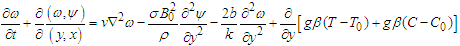 | (15) |
where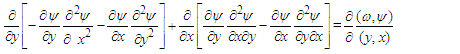 | (16) |
Substituting (9) into (4) leads to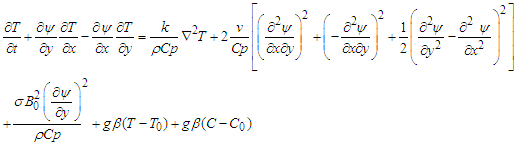 | (17) |
Further simplifying of (17) resulted into 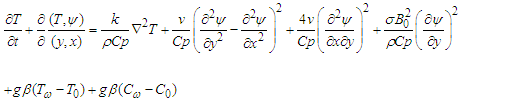 | (18) |
Similarly substituting (9) into (5) using the same approach as in above leads to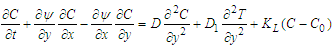 | (19) |
Simplifying equation (19) further to obtain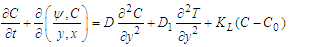 | (20) |
The corresponding boundary conditions are: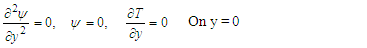 | (21) |
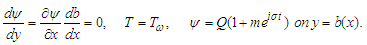 | (22) |
The function b(x) is assumed to depend upon a small parameter 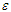 such that
such that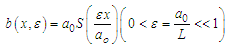 | (23) |
where 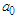 the characteristics constant half width of the channel, L is the characteristics constant length of the channel and S is the function describing the channel wall divergence geometry. This assumption helps us to simplify the problem by writing the equations in non-dimensional form.To achieve this,
the characteristics constant half width of the channel, L is the characteristics constant length of the channel and S is the function describing the channel wall divergence geometry. This assumption helps us to simplify the problem by writing the equations in non-dimensional form.To achieve this, 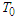 is defined as the reference temperature and the following non-dimensional qualities were introduced.
is defined as the reference temperature and the following non-dimensional qualities were introduced.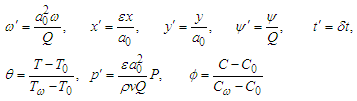 | (24) |
Differentiating (24) with respect to x, y and t the non-dimensional quantities and Substituting into (15, 17, 18, 19) and after neglecting terms of order 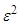 and higher order as well as the primes for charity to obtain
and higher order as well as the primes for charity to obtain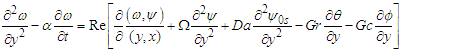 | (25) |
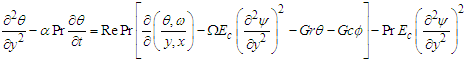 | (26) |
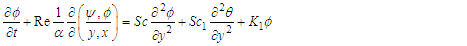 | (27) |
Where 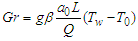 thermal Grashof number,
thermal Grashof number, 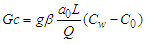 mass Grashof number,
mass Grashof number,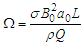 is the magnetic field intensity parameter
is the magnetic field intensity parameter 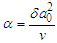 the womersley number,
the womersley number, 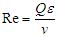 the effective Reynolds number
the effective Reynolds number 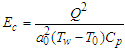 is the Eckert number
is the Eckert number 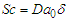 Schmitt number and
Schmitt number and 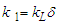 chemical reaction number and
chemical reaction number and 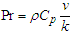 the prandlt number.The boundary conditions are:
the prandlt number.The boundary conditions are: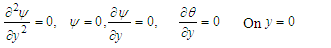 | (28) |
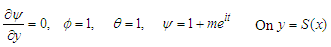 | (29) |
Due to the nonlinear nature of the equations, it is convenient to adopt a power series expansion with the effective flow Reynolds number (Re) as follows: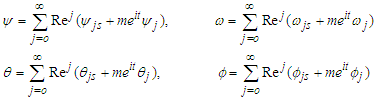 | (30) |
where 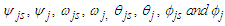 are functions of
are functions of 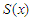 and y. it is important to note that the real part of the equation (30) forms the solution of the problem which is physically meaningful. Substituting equation (30) into equations (25-27) and collecting terms of like order of Re and
and y. it is important to note that the real part of the equation (30) forms the solution of the problem which is physically meaningful. Substituting equation (30) into equations (25-27) and collecting terms of like order of Re and 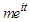 , gives zero order:
, gives zero order: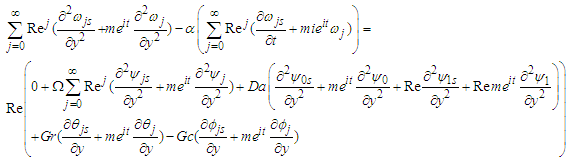 | (31) |
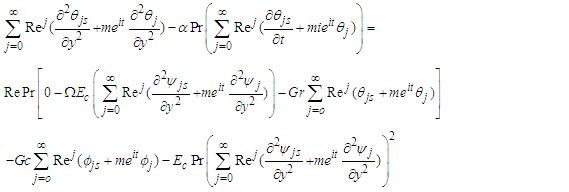 | (32) |
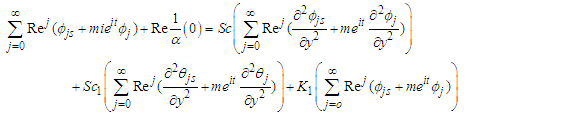 | (33) |
when j = 0, and collecting terms of like order of 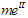 , lead to Zero order (31), (32) and (33) yields
, lead to Zero order (31), (32) and (33) yields 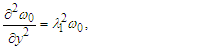 | (34) |
 | (35) |
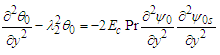 | (36) |
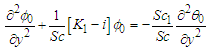 | (37) |
Considering the term js in (32), (32) and (33) the following set of equations were obtained. 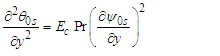 | (38) |
 | (39) |
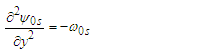 | (40) |
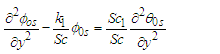 | (41) |
The boundary conditions are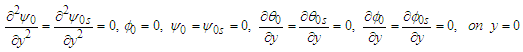 | (42) |
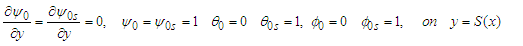 | (43) |
When j = 1 order 1 gives: | (44) |
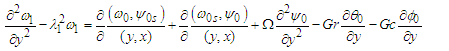 | (45) |
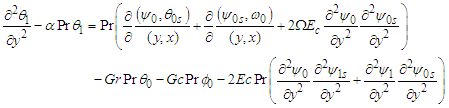 | (46) |
 | (47) |
Considering the term js the following set of equations were obtained.  | (48) |
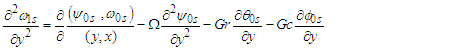 | (49) |
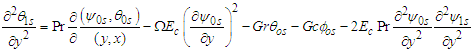 | (50) |
 | (51) |
We now solving the following equations: (34), (35), (36), (37), (38), (39), (40), (41), (42), (43), (44), (45), (46) (47), (48), (49), (50) and (51) and the stream function 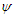 , vorticity
, vorticity 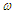 , temperature distribution
, temperature distribution 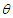 and volume fraction
and volume fraction 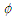 were obtained thus:
were obtained thus: | (52) |
 | (53) |
 | (54) |
 | (55) |
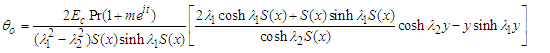 | (56) |
 | (57) |
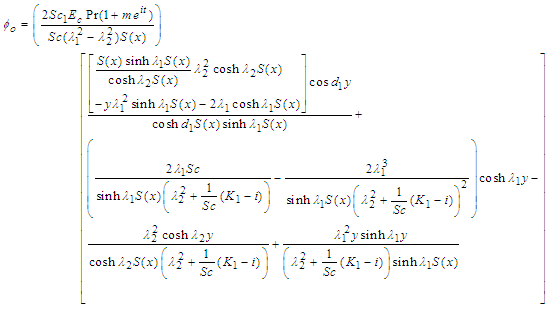 | (58) |
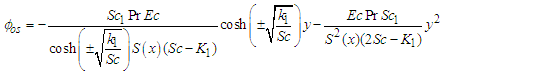 | (59) |
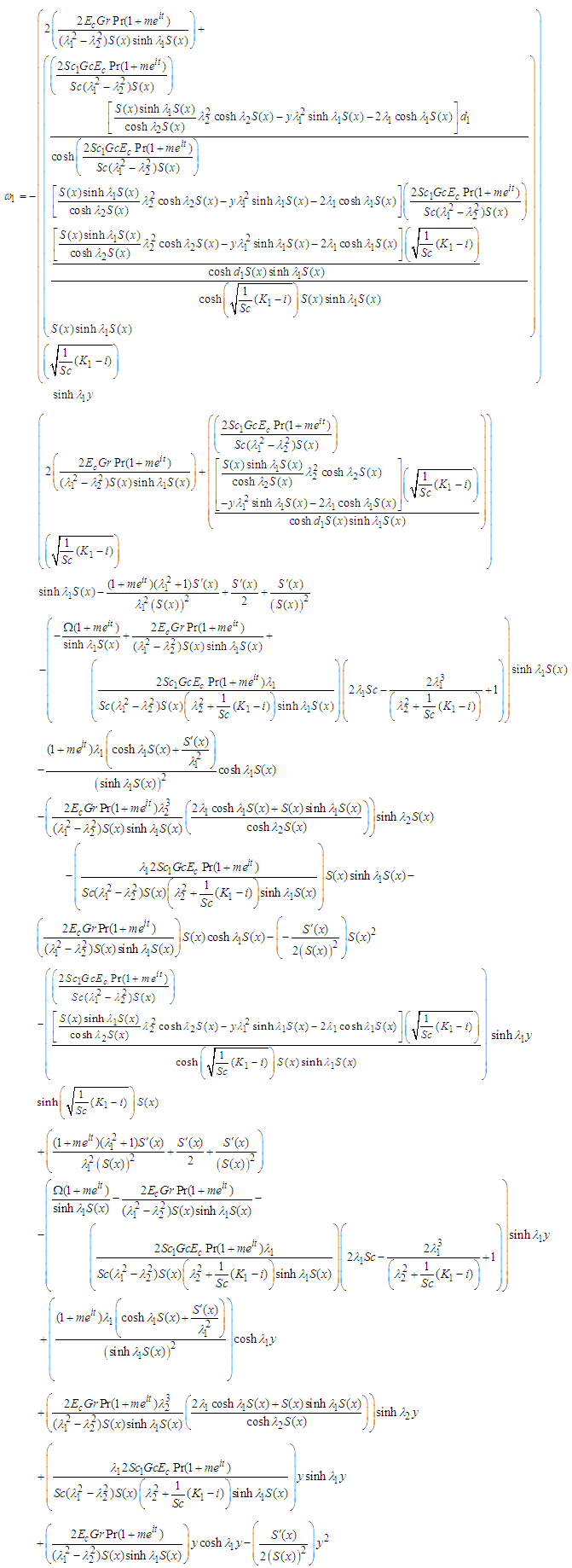 | (60) |
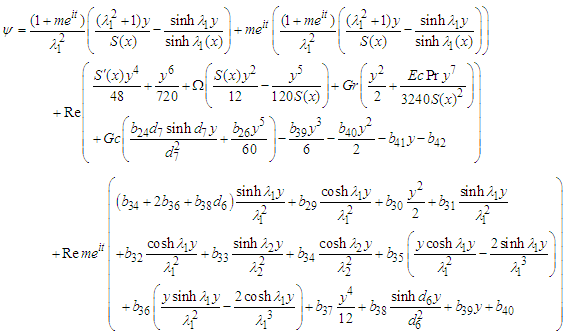 | (61) |
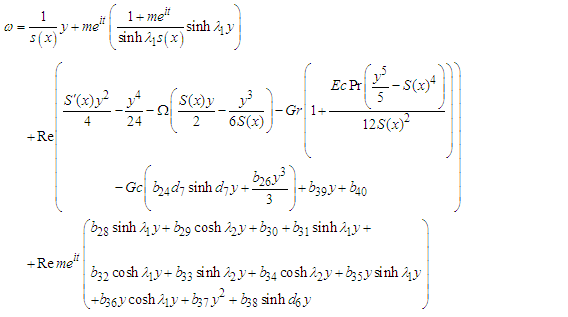 | (62) |
 | (63) |
 | (64) |
where: | (65) |
 | (66) |
 | (67) |
 | (68) |
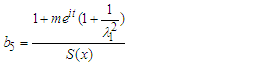 | (69) |
 | (70) |
 | (71) |
 | (72) |
 | (73) |
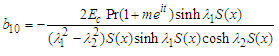 | (74) |
 | (75) |
 | (76) |
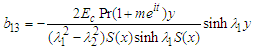 | (77) |
 | (78) |
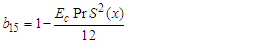 | (79) |
 | (80) |
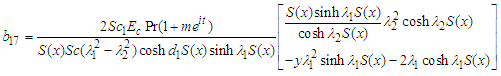 | (81) |
 | (82) |
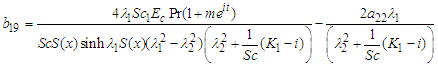 | (83) |
 | (84) |
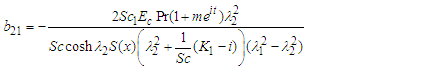 | (85) |
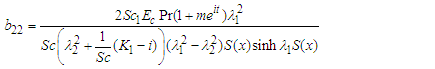 | (86) |
 | (87) |
 | (89) |
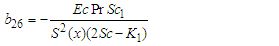 | (90) |
 | (91) |
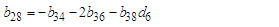 | (92) |
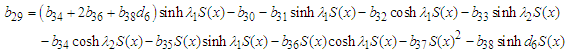 | (93) |
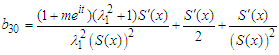 | (94) |
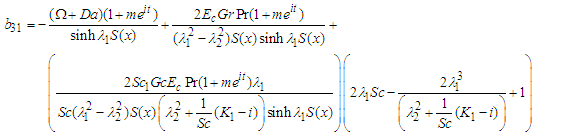 | (95) |
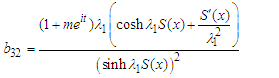 | (96) |
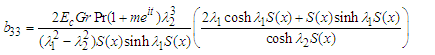 | (97) |
 | (98) |
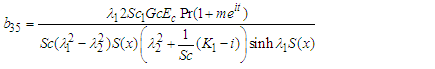 | (99) |
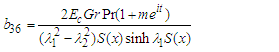 | (100) |
 | (101) |
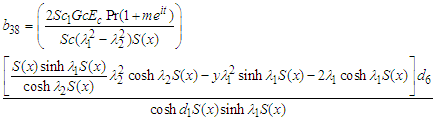 | (102) |
 | (103) |
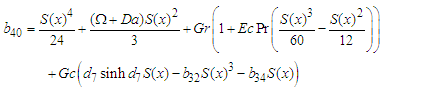 | (104) |
 | (105) |
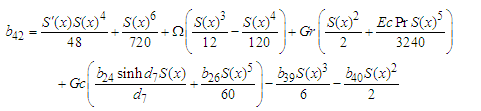 | (106) |
 | (107) |
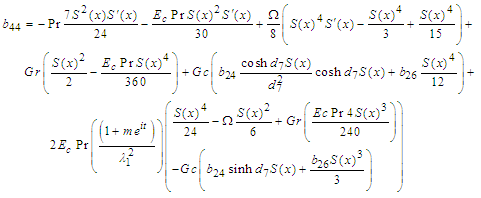 | (108) |
 | (109) |
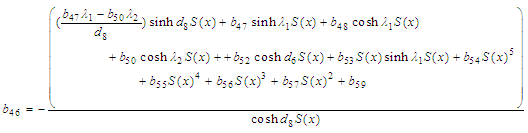 | (110) |
 | (111) |
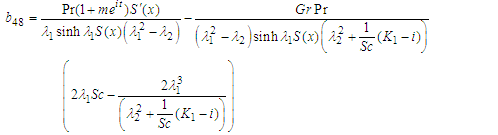 | (112) |
 | (113) |
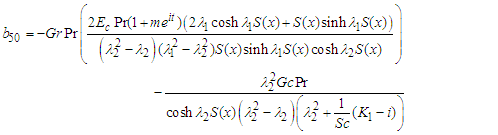 | (114) |
 | (115) |
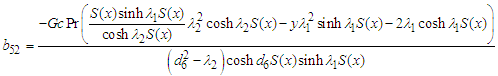 | (116) |
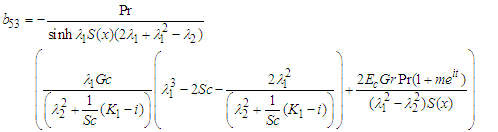 | (117) |
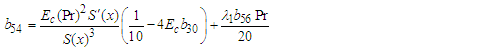 | (118) |
 | (119) |
 | (120) |
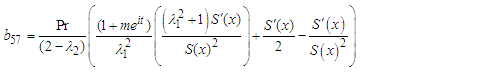 | (121) |
 | (122) |
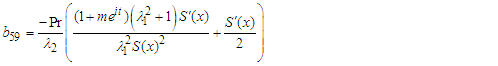 | (123) |
 | (124) |
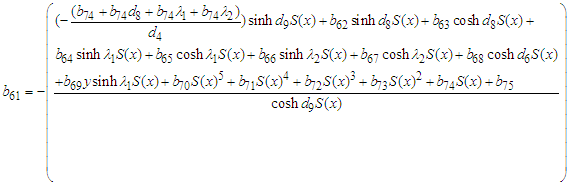 | (125) |
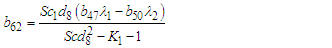 | (126) |
 | (127) |
 | (128) |
 | (129) |
 | (130) |
 | (131) |
 | (132) |
 | (133) |
 | (134) |
 | (135) |
 | (136) |
 | (137) |
 | (138) |
 | (139) |
 | (140) |
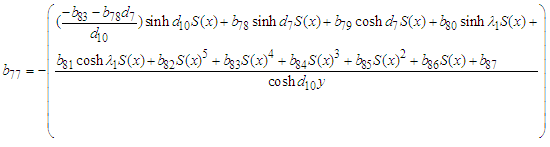 | (141) |
 | (142) |
 | (143) |
 | (144) |
 | (145) |
 | (146) |
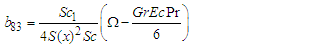 | (147) |
 | (148) |
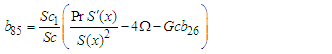 | (149) |
 | (150) |
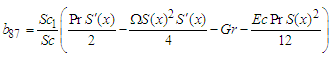 | (151) |
 | (152) |
 | (153) |
 | (154) |
 | (155) |
 | (156) |
4. Method of Solution
The problems of consideration are solved analytically which resulted into the graphical results under results and discussion.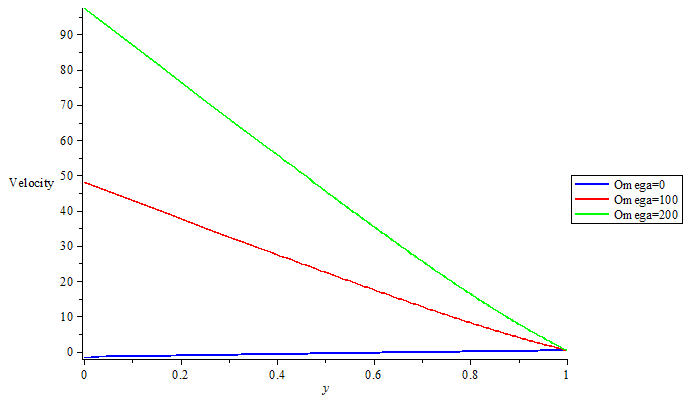 | Figure 1. Velocity profile for different value of magnetic field intensity parameters |
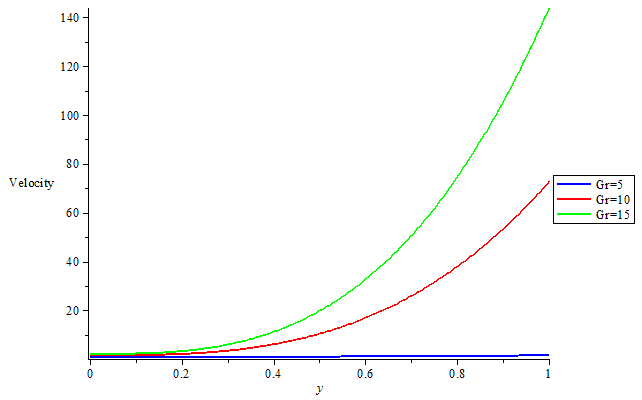 | Figure 2. Velocity profile for different value of thermal Grashof numbers |
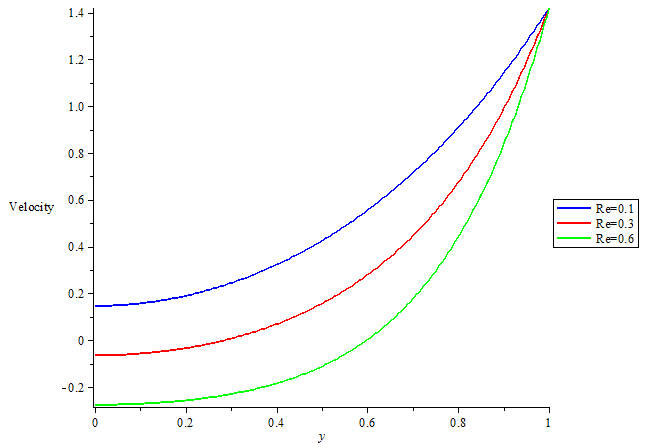 | Figure 3. Velocity profile for different value of Reynolds numbers |
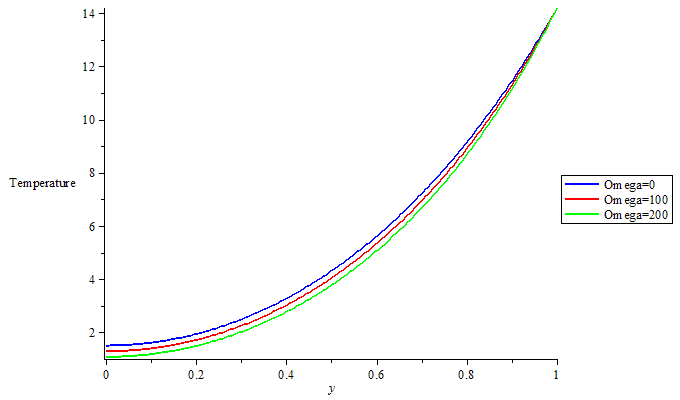 | Figure 4. Temperature profile for different value of magnetic field intensity parameters |
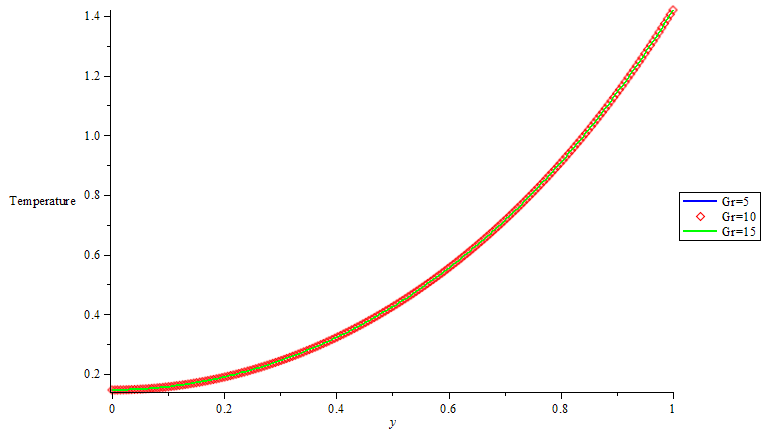 | Figure 5. Temperature profile for different value of thermal Grashof numbers |
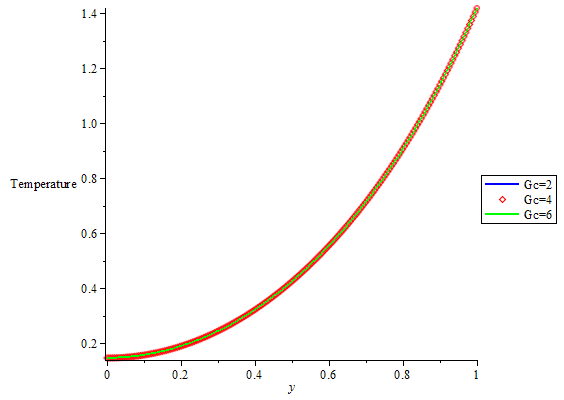 | Figure 6. Temperature profile for different value of Mass Grashof numbers |
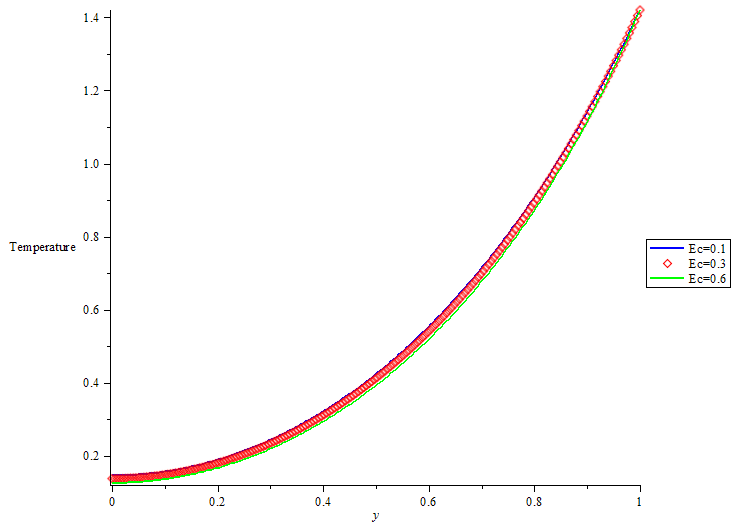 | Figure 7. Temperature profile for different value of Eckert numbers |
5. Results and Discussion
In order to study the behaviour of velocity, temperature and concentration profile, a comprehensive numerical computation using mathematical software Maple 12 was carried out for various values of the parameters that describe the flow characteristics, and the results were reported in terms of graphs as shown in figures (1)- (7). The pulse m was chosen small so that the ensuring flow is a small oscillatory disturbance about the steady flow. We have observed that for every m, the womersley parameter 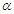 can be varied only for a range of values, hence we set
can be varied only for a range of values, hence we set 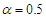 . The effect of varying the Reynolds number Re, the Eckert number
. The effect of varying the Reynolds number Re, the Eckert number 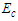 and the Prandtl number Pr to flow structure were observed. Therefore we set
and the Prandtl number Pr to flow structure were observed. Therefore we set 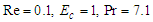 in the ensuring analysis, we assume that m and
in the ensuring analysis, we assume that m and 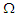 can be varied while keeping
can be varied while keeping 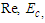 and
and 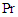 fixed. This assumption is valid because the physics of the problem and the range of values of m and
fixed. This assumption is valid because the physics of the problem and the range of values of m and 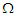 that are involved. When the porosity was considered, figure1 shows that the effect of increasing values of
that are involved. When the porosity was considered, figure1 shows that the effect of increasing values of 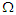 on steady flow is to dampen the velocity profile. This is well known for Hartmann flow. And with increase in Magnetic field intensity parameter (omega) numbers there is Velocity increase which pushed the flow to the wall of the channel that leads to increase in heat along the wall of the channel thereby increasing the velocity in the boundary layer. This is depicted in Figure 2 with increase in thermal Grashof numbers the velocity increase and the flow were pushed away from the wall. This suggests that unsteadiness has the effect of cooling the fluid. For increase in Reynolds number velocity decreases as shown in figure 3. This suggests that in this model, increasing Reynolds number enhances unsteadiness. The pressure gradient, which is trying to accelerate the fluid, is counteracted by the magnetic drag. Figure 4 shows that there is slight decrease in temperature as Magnetic field intensity parameter (omega) increases. The effect of thermal Grashof number and mass Grashof number in figure 5 but not well felt on temperature in figure 6 there is a slight increase in temperature as Eckert number increase in figure 7.
on steady flow is to dampen the velocity profile. This is well known for Hartmann flow. And with increase in Magnetic field intensity parameter (omega) numbers there is Velocity increase which pushed the flow to the wall of the channel that leads to increase in heat along the wall of the channel thereby increasing the velocity in the boundary layer. This is depicted in Figure 2 with increase in thermal Grashof numbers the velocity increase and the flow were pushed away from the wall. This suggests that unsteadiness has the effect of cooling the fluid. For increase in Reynolds number velocity decreases as shown in figure 3. This suggests that in this model, increasing Reynolds number enhances unsteadiness. The pressure gradient, which is trying to accelerate the fluid, is counteracted by the magnetic drag. Figure 4 shows that there is slight decrease in temperature as Magnetic field intensity parameter (omega) increases. The effect of thermal Grashof number and mass Grashof number in figure 5 but not well felt on temperature in figure 6 there is a slight increase in temperature as Eckert number increase in figure 7.
6. Conclusions
A model was formulated with the inclusion of concentration equation. The study added porosity parameter to explain viscous dissipation in a porous vertical channel. Approximate numerical solutions were found using regular perturbation technique together with their boundary condition. The outcome of study showed that increase in viscous dissipation led to decrease in Temperature and velocity profile but not in concentration. The porosity effect on heat and mass transfer were clearly exposed with the significance of the parameters introduced. Overall observations based on the problem formulated and analysed upon which conclusions were drawn and listed as:i. evaluated the effect of porosity on heat and mass transfer of natural convection fluid flow in porous media;ii. assessed the impacts of porosity on heat and mass transfer of MHD fluid flow in porous media;iii. established the influence of MHD fluid flow on vertically porous channel; andiv. determined the effects of porosity on heat and mass transfer of MHD fluid flow in a vertically porous channel. Limitation exhibited by the methods used was that: The porosity effect on heat and mass transfer over a vertical porous channel was considered. The resulting governing equations were simplified and solved using perturbation technique. The results are presented in graphical forms. The impact of variations of velocity, temperature and concentration parameters on non-dimensional variables of the heat and mass transfer was established to explain porosity heat and mass transfer of MHD fluid flow in porous vertical channel. The influence of porosity effects were also noticed along with other listed parameters and these contributed chronologically to MHD fluid flow thereby explaining heat and mass transfer over porous vertical channel. The study concluded that increase in mass Grashof, thermal Grashof, magnetic parameter; womersley parameters, Reynolds, Eckert, Schmidt and chemical reaction numbers had significant effects on the MHD fluid flow in porous vertical channel.
Nomenclature
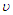 = The kinematics Viscosity coefficient
= The kinematics Viscosity coefficient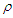 = The fluid density
= The fluid density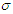 = Electrical conductivity of the fluid
= Electrical conductivity of the fluid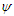 = Stream functionC = Concentration of the fluid within the boundary layer.
= Stream functionC = Concentration of the fluid within the boundary layer.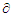 = A volume flux with oscillating frequencym = Pulse
= A volume flux with oscillating frequencym = Pulse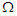 = Magnetic field intensity parameter (Omega)Re = Effective flow Reynolds number
= Magnetic field intensity parameter (Omega)Re = Effective flow Reynolds number 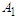 = Womersley numberGr = Thermal Grashof number Gc = Mass Grashof number
= Womersley numberGr = Thermal Grashof number Gc = Mass Grashof number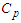 = Specific heat at constant pressureT = Temperature in the boundary layer
= Specific heat at constant pressureT = Temperature in the boundary layer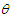 = Non-dimensional temperature
= Non-dimensional temperature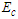 = Eckert numberP = PressureU = Velocity component in the x-directionV = Velocity component in the y-directiont = TimeSc = Schmidt number
= Eckert numberP = PressureU = Velocity component in the x-directionV = Velocity component in the y-directiont = TimeSc = Schmidt number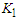 = Chemical reaction numberu, v, w = Cartesian velocity componentsx, y, z = Cartesian coordinatesQ = The flux rate across any section of the channel.K = The wall slip parameter.B0 = The electromagnetic induction µ = The magnetic permeabilityH0 = The intensity of magnetic fieldA = The characteristic half-width of the channel
= Chemical reaction numberu, v, w = Cartesian velocity componentsx, y, z = Cartesian coordinatesQ = The flux rate across any section of the channel.K = The wall slip parameter.B0 = The electromagnetic induction µ = The magnetic permeabilityH0 = The intensity of magnetic fieldA = The characteristic half-width of the channel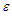 = A small dimensionless parameter that specifies the slow variation in the cross- section of the channelL = The channel characteristic lengthY = ±b(x) are the rigid and impermeable walls of the channelPr = Prandlt number
= A small dimensionless parameter that specifies the slow variation in the cross- section of the channelL = The channel characteristic lengthY = ±b(x) are the rigid and impermeable walls of the channelPr = Prandlt number
References
| [1] | Ahammad M.U. Mollah Md. S.H. (2011) Numerical sturdy of MHD free convection flow and mass transfer over a stretching sheet considering Dufour and Soret effects in the presence of magnetic field, international Journal of Engineering and Technology, 11(05): 4-11. |
| [2] | Attia H.A. (2006) Unsteady MHD couette flow and heat transfer of dusty with variable physical properties Applied Mathematics and Computation, 177 308-318. |
| [3] | Chakraborty S. (2001) MHD flow and heat transfer of a dusty viscoelastic stratified fluid down an inclined channel in porous medium under variables viscosity. Theoretical and Applied Mechanics Vol.26, pp. 1-14. 4. |
| [4] | Hazarika G.C. and Jadav Konch (2014), Effects of variable viscosity and thermal conductivity on MHD free convective flow along a vertical porous plate with viscous dissipation “International journal of mathematics trends and technology –volume 15 number 1. |
| [5] | Mhone, P.Y. and Makinde, O.D (2006). “Unsteady MHD flow with heat transfer in a diverging channel” Rom. journ Phys. Vol. 51. Nos. 9-10, pp.967-979, Bucharest. |
| [6] | Palani G. and Ganesan P. (2007), Heat Transfer Effects on Dusty Gas Flow past a Semi- Infinite Inclined plate forsch Ingenieurwes, Vol. 71, pp 223-230. |
| [7] | Seddeek, M. A. and Salama, F. A. (2007), The effects of temperature dependent viscosity and thermal conductivity on unsteady MHD convective heat transfer past a semi-infinite vertical porous moving plate with variable suction. Computational Materials Science, Vol. 40(2), pp. 186-192. |
| [8] | Soundalgekar V.M., Gupta SK. and Birajdar NS. (1979), Effects of Mass transfer and free convection currents on MHD Stokes problem for a vertical plate. Nuclear Engineering Design, vol.53, pp.339-346. |
| [9] | Taneja, R and Jain, N. C (Jan 2004): MHD flow with slips effects and temperature dependent heat source in a viscous incompressible fluid confined between a long vertical wavy wall and a parallel flat wall. Def. Sc. J., 21 - 29. |



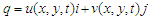
 (a)through a symmetric vertical channel (
(a)through a symmetric vertical channel (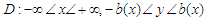 ) where (
) where (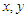 ) are Cartesian co-ordinates such that
) are Cartesian co-ordinates such that 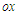 is the axis of symmetry of the channel and
is the axis of symmetry of the channel and 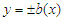 are the rigid and impermeable walls of the channel. The walls of the channel are kept at a constant temperature
are the rigid and impermeable walls of the channel. The walls of the channel are kept at a constant temperature 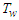 . The fluid is incompressible with uniform properties i.e. density
. The fluid is incompressible with uniform properties i.e. density 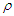 , kinematic viscosity
, kinematic viscosity 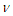 and electrical conductivity
and electrical conductivity 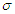 . A volume flux with oscillating frequency
. A volume flux with oscillating frequency 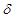 and pulse m is prescribed as in figure 1 below:
and pulse m is prescribed as in figure 1 below:
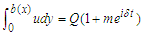
 (b)A uniform magnetic force is applied in the
(b)A uniform magnetic force is applied in the 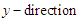 . A very small magnetic Reynolds number is assumed and therefore the induced magnetic field is neglected. Two key physical effects occur when the fluid moves into the magnetic field; the first one is that an electric field E is induced in the flow. There is no excess charge density and then
. A very small magnetic Reynolds number is assumed and therefore the induced magnetic field is neglected. Two key physical effects occur when the fluid moves into the magnetic field; the first one is that an electric field E is induced in the flow. There is no excess charge density and then 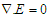 . Neglecting the induced magnetic field implies that
. Neglecting the induced magnetic field implies that 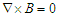 and therefore the induced electric field is negligible. The second key effect is dynamical i.e. a Lorentz force
and therefore the induced electric field is negligible. The second key effect is dynamical i.e. a Lorentz force 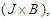 where J is the current density acts on the fluid and modifies its motion. Therefore, there is a transfer of energy
where J is the current density acts on the fluid and modifies its motion. Therefore, there is a transfer of energy 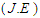 from the electromagnetic field to the fluid. In this study, relativistic effects are neglected, and J is given by Ohm’s law:
from the electromagnetic field to the fluid. In this study, relativistic effects are neglected, and J is given by Ohm’s law: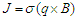
 (c)Within the framework of these assumptions the magneto-hydrodynamic flow relevant to the problem is governed by the set of equations.
(c)Within the framework of these assumptions the magneto-hydrodynamic flow relevant to the problem is governed by the set of equations.
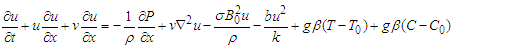

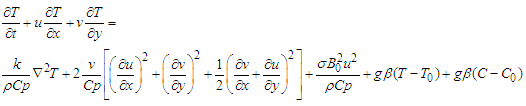
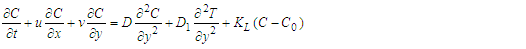
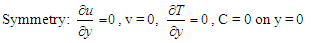
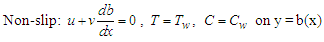
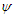 defined by
defined by 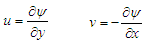
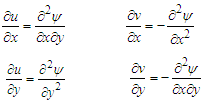

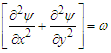 Which can be written as
Which can be written as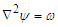
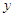 and (3) with respect to
and (3) with respect to 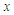 gives
gives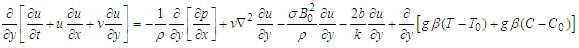
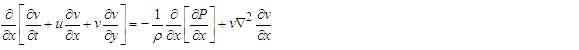
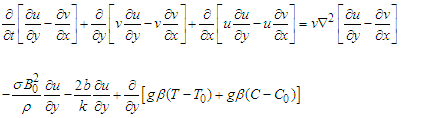
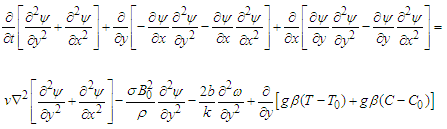
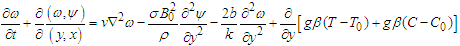
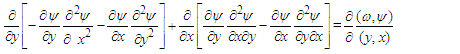
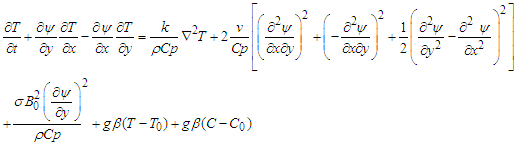
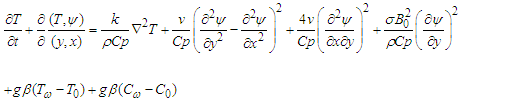
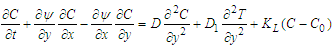
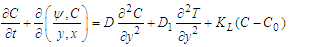
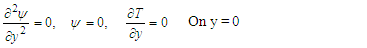
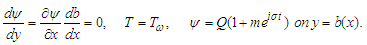
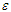 such that
such that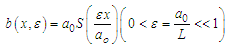
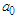 the characteristics constant half width of the channel, L is the characteristics constant length of the channel and S is the function describing the channel wall divergence geometry. This assumption helps us to simplify the problem by writing the equations in non-dimensional form.To achieve this,
the characteristics constant half width of the channel, L is the characteristics constant length of the channel and S is the function describing the channel wall divergence geometry. This assumption helps us to simplify the problem by writing the equations in non-dimensional form.To achieve this, 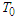 is defined as the reference temperature and the following non-dimensional qualities were introduced.
is defined as the reference temperature and the following non-dimensional qualities were introduced.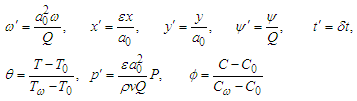
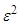 and higher order as well as the primes for charity to obtain
and higher order as well as the primes for charity to obtain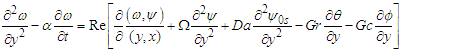
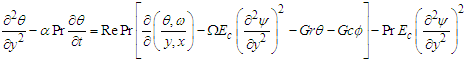
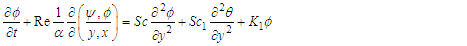
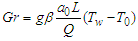 thermal Grashof number,
thermal Grashof number, 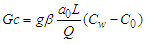 mass Grashof number,
mass Grashof number,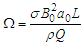 is the magnetic field intensity parameter
is the magnetic field intensity parameter 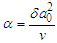 the womersley number,
the womersley number, 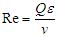 the effective Reynolds number
the effective Reynolds number 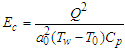 is the Eckert number
is the Eckert number 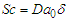 Schmitt number and
Schmitt number and 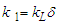 chemical reaction number and
chemical reaction number and 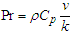 the prandlt number.The boundary conditions are:
the prandlt number.The boundary conditions are: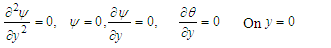
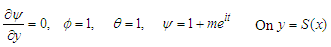
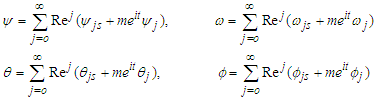
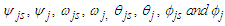 are functions of
are functions of 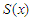 and y. it is important to note that the real part of the equation (30) forms the solution of the problem which is physically meaningful. Substituting equation (30) into equations (25-27) and collecting terms of like order of Re and
and y. it is important to note that the real part of the equation (30) forms the solution of the problem which is physically meaningful. Substituting equation (30) into equations (25-27) and collecting terms of like order of Re and 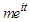 , gives zero order:
, gives zero order: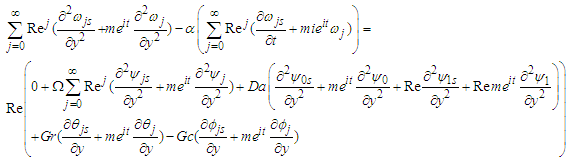
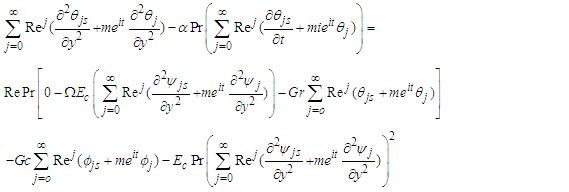
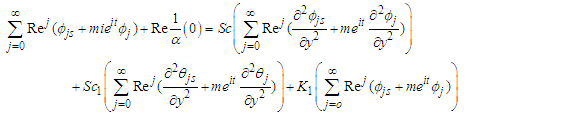
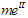 , lead to Zero order (31), (32) and (33) yields
, lead to Zero order (31), (32) and (33) yields 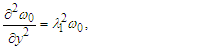

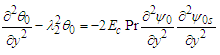
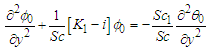
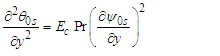

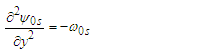
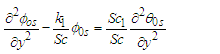
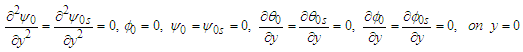
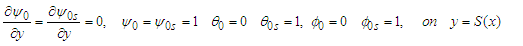

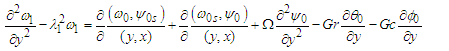
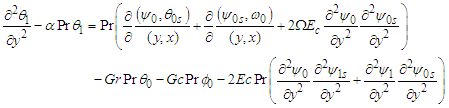


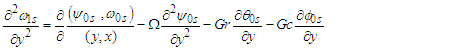
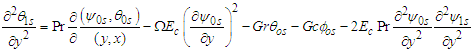

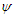 , vorticity
, vorticity 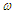 , temperature distribution
, temperature distribution 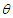 and volume fraction
and volume fraction 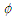 were obtained thus:
were obtained thus:



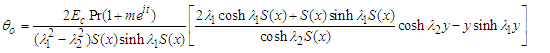

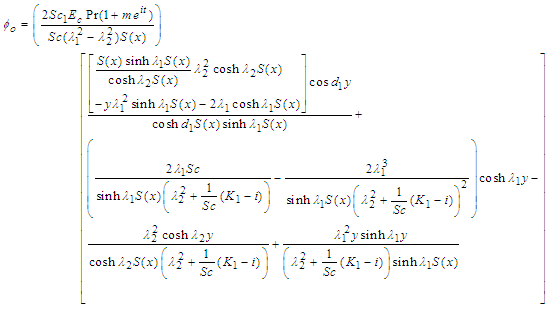
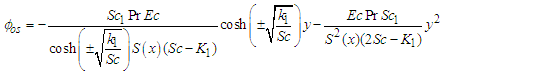

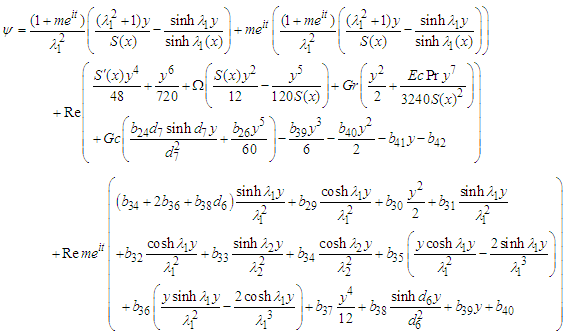
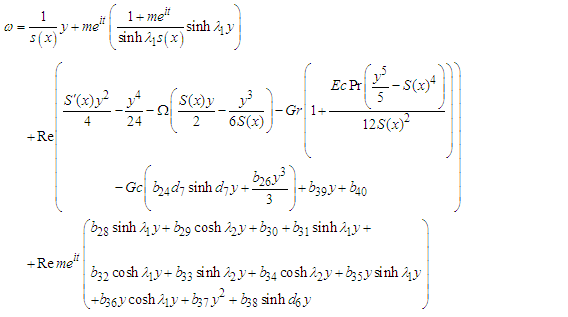






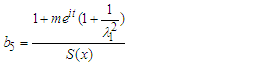




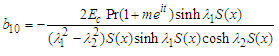


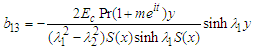

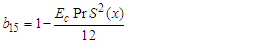

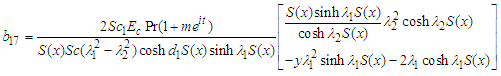

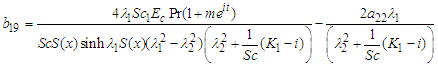

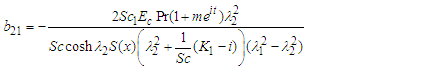
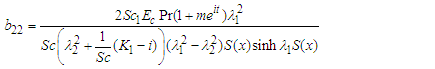


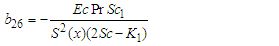

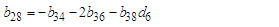
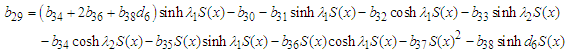
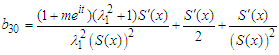
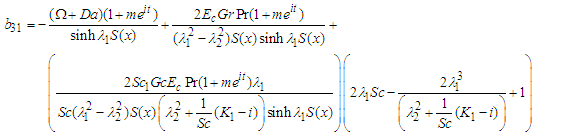
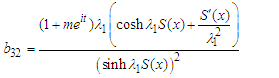
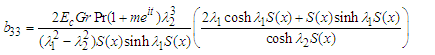

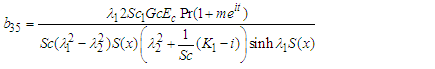
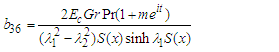

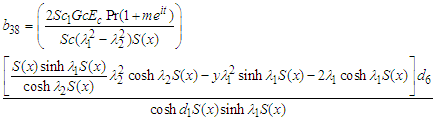

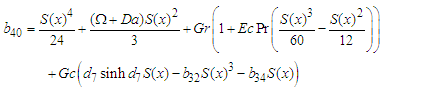

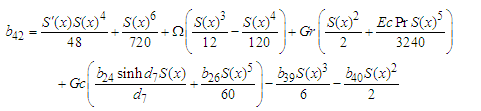

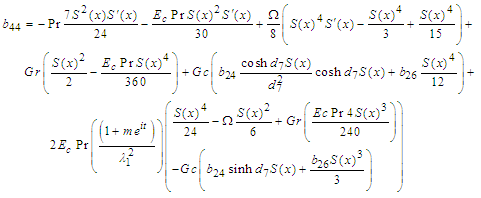

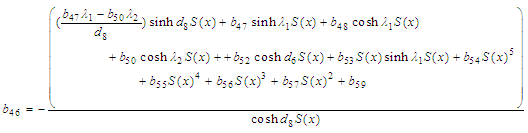

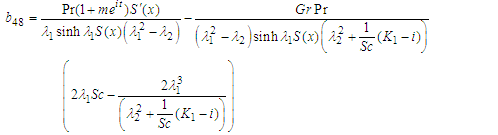

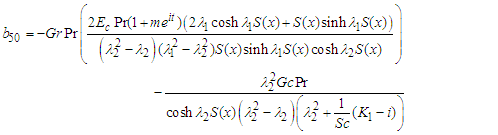

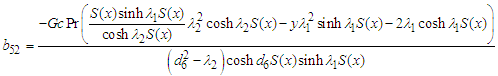
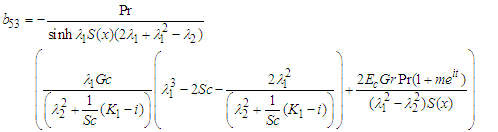
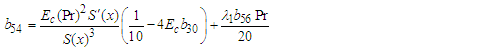


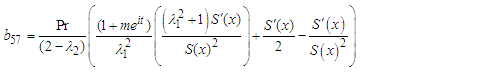

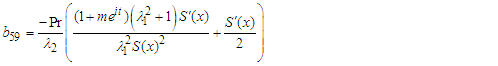

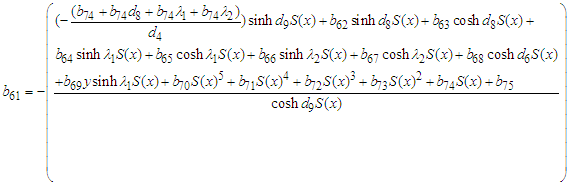
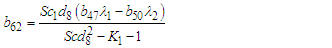














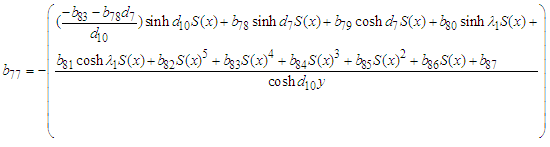





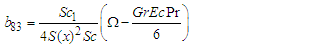

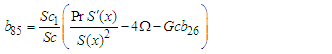

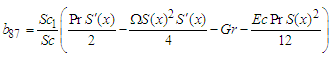












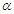 can be varied only for a range of values, hence we set
can be varied only for a range of values, hence we set 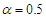 . The effect of varying the Reynolds number Re, the Eckert number
. The effect of varying the Reynolds number Re, the Eckert number 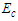 and the Prandtl number Pr to flow structure were observed. Therefore we set
and the Prandtl number Pr to flow structure were observed. Therefore we set 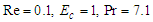 in the ensuring analysis, we assume that m and
in the ensuring analysis, we assume that m and 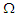 can be varied while keeping
can be varied while keeping 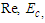 and
and 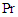 fixed. This assumption is valid because the physics of the problem and the range of values of m and
fixed. This assumption is valid because the physics of the problem and the range of values of m and 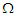 that are involved. When the porosity was considered, figure1 shows that the effect of increasing values of
that are involved. When the porosity was considered, figure1 shows that the effect of increasing values of 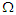 on steady flow is to dampen the velocity profile. This is well known for Hartmann flow. And with increase in Magnetic field intensity parameter (omega) numbers there is Velocity increase which pushed the flow to the wall of the channel that leads to increase in heat along the wall of the channel thereby increasing the velocity in the boundary layer. This is depicted in Figure 2 with increase in thermal Grashof numbers the velocity increase and the flow were pushed away from the wall. This suggests that unsteadiness has the effect of cooling the fluid. For increase in Reynolds number velocity decreases as shown in figure 3. This suggests that in this model, increasing Reynolds number enhances unsteadiness. The pressure gradient, which is trying to accelerate the fluid, is counteracted by the magnetic drag. Figure 4 shows that there is slight decrease in temperature as Magnetic field intensity parameter (omega) increases. The effect of thermal Grashof number and mass Grashof number in figure 5 but not well felt on temperature in figure 6 there is a slight increase in temperature as Eckert number increase in figure 7.
on steady flow is to dampen the velocity profile. This is well known for Hartmann flow. And with increase in Magnetic field intensity parameter (omega) numbers there is Velocity increase which pushed the flow to the wall of the channel that leads to increase in heat along the wall of the channel thereby increasing the velocity in the boundary layer. This is depicted in Figure 2 with increase in thermal Grashof numbers the velocity increase and the flow were pushed away from the wall. This suggests that unsteadiness has the effect of cooling the fluid. For increase in Reynolds number velocity decreases as shown in figure 3. This suggests that in this model, increasing Reynolds number enhances unsteadiness. The pressure gradient, which is trying to accelerate the fluid, is counteracted by the magnetic drag. Figure 4 shows that there is slight decrease in temperature as Magnetic field intensity parameter (omega) increases. The effect of thermal Grashof number and mass Grashof number in figure 5 but not well felt on temperature in figure 6 there is a slight increase in temperature as Eckert number increase in figure 7.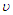 = The kinematics Viscosity coefficient
= The kinematics Viscosity coefficient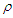 = The fluid density
= The fluid density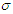 = Electrical conductivity of the fluid
= Electrical conductivity of the fluid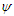 = Stream functionC = Concentration of the fluid within the boundary layer.
= Stream functionC = Concentration of the fluid within the boundary layer.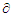 = A volume flux with oscillating frequencym = Pulse
= A volume flux with oscillating frequencym = Pulse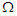 = Magnetic field intensity parameter (Omega)Re = Effective flow Reynolds number
= Magnetic field intensity parameter (Omega)Re = Effective flow Reynolds number 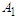 = Womersley numberGr = Thermal Grashof number Gc = Mass Grashof number
= Womersley numberGr = Thermal Grashof number Gc = Mass Grashof number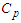 = Specific heat at constant pressureT = Temperature in the boundary layer
= Specific heat at constant pressureT = Temperature in the boundary layer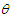 = Non-dimensional temperature
= Non-dimensional temperature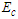 = Eckert numberP = PressureU = Velocity component in the x-directionV = Velocity component in the y-directiont = TimeSc = Schmidt number
= Eckert numberP = PressureU = Velocity component in the x-directionV = Velocity component in the y-directiont = TimeSc = Schmidt number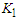 = Chemical reaction numberu, v, w = Cartesian velocity componentsx, y, z = Cartesian coordinatesQ = The flux rate across any section of the channel.K = The wall slip parameter.B0 = The electromagnetic induction µ = The magnetic permeabilityH0 = The intensity of magnetic fieldA = The characteristic half-width of the channel
= Chemical reaction numberu, v, w = Cartesian velocity componentsx, y, z = Cartesian coordinatesQ = The flux rate across any section of the channel.K = The wall slip parameter.B0 = The electromagnetic induction µ = The magnetic permeabilityH0 = The intensity of magnetic fieldA = The characteristic half-width of the channel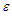 = A small dimensionless parameter that specifies the slow variation in the cross- section of the channelL = The channel characteristic lengthY = ±b(x) are the rigid and impermeable walls of the channelPr = Prandlt number
= A small dimensionless parameter that specifies the slow variation in the cross- section of the channelL = The channel characteristic lengthY = ±b(x) are the rigid and impermeable walls of the channelPr = Prandlt number Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML