Syed Tahirul Husnain1, Tooba Feroze2
1Bahria College, Zafar Campus, Street 34, Sector E-8, Pakistan Naval Complex, Islamabad, Pakistan
2School of Natural Sciences, National University of Sciences and Technology, H-12, Islamabad, Pakistan
Correspondence to: Tooba Feroze, School of Natural Sciences, National University of Sciences and Technology, H-12, Islamabad, Pakistan.
| Email: |  |
Copyright © 2021 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
Sophus Lie developed technique to obtain solutions of differential equations using continuous symmetries. Using these continuous symmetries, Peter E. Hydon developed technique to obtain discrete symmetries which led to finding further new solutions of the underlying equations. In this paper continuous and discrete symmetries of Korteweg de Vries and nonlinear filtration equations are analyzed. Using these symmetries group invariant solutions and the exact solutions of these equations are obtained.
Keywords:
Continuous symmetries, Discrete symmetries, Group invariant solutions
Cite this paper: Syed Tahirul Husnain, Tooba Feroze, Symmetries and Exact Solutions of Some Partial Differential Equations, International Journal of Mechanics and Applications, Vol. 10 No. 2, 2021, pp. 27-29. doi: 10.5923/j.mechanics.20211002.01.
1. Introduction
Differential equations is an important branch of mathematics. Since the time of Leibneiz and Newton, different attempts have been made to develop techniques for finding their solutions. The process is still going on.In this context, Sophus Lie developed a technique known as group theoretic/symmetry methods for finding the solutions of differential equations. His method is, though, highly algorithmic but has an advantage that if the symmetry of that differential equation exists then it either gives the solution or reduce the problem into a comparatively simpler one. The symmetries used in his methods are continuous i.e. they depend upon some parameter [1]-[3]. In contrast to continuous symmetries there are other symmetries known as discrete symmetries which do not depend on parameter. However, these discrete symmetries are also useful in finding solutions of differential equations. Using continuous symmetries, Peter E. Hydon developed a technique [4]-[8] to get all discrete symmetries of differential equations. His technique has been used here to get all discrete symmetries of nonlinear filtration equation. Exact solutions, using these symmetries are then presented.Hydon considered an automorphism of 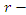 dimensional Lie algebra L of symmetries of differential equations. This gives a change in basis vectors and is represented as
dimensional Lie algebra L of symmetries of differential equations. This gives a change in basis vectors and is represented as 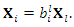 | (1) |
As the structure constants do change under a transformation of the basis, we have the following transformation law 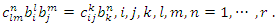 | (2) |
These constraints, called the nonlinear constraints. provide a real-valued matrix 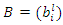 that corresponds to the automorphism. They fix some of the entries of matrix
that corresponds to the automorphism. They fix some of the entries of matrix 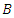 . The adjoint action of each basis vector,
. The adjoint action of each basis vector, 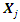 , generates a one-parameter Lie group of inner automorphisms whose matrix representation is [4]
, generates a one-parameter Lie group of inner automorphisms whose matrix representation is [4] 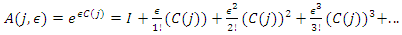 | (3) |
where 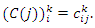 | (4) |
The matrix 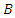 can be further simplified with the help of
can be further simplified with the help of 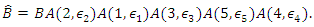 | (5) |
The simplified matrix is then used to write determining equation whose solution is of the form 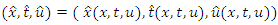 | (6) |
from where we get all the symmetries, i.e. both continuous and discrete.
2. Symmetries of Korteweg de Vries Equation
Korteweg de Vries (KdV) equation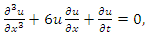 | (7) |
is a mathematical model of waves on shallow water surfaces. Many different variations of the KdV equation have been studied. The mathematical theory behind the KdV equation is a topic of active research. KdV equation was first introduced by Boussinesq (1877) and rediscovered by Diederik Korteweg and Gustav de Vries (1895).Following are the basis elements and nonzero structure constants of the 4-dimensional Lie algebra of KdV equation (7) 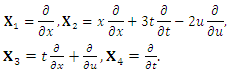 | (8) |
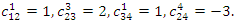 | (9) |
The corresponding (one-parameter) Lie groups of point symmetries 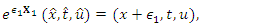 | (10) |
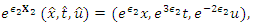 | (11) |
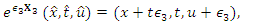 | (12) |
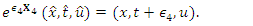 | (13) |
The only discrete point symmetry of the KdV equation (7) is 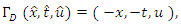 | (14) |
which can easily be obtained by following theprocedure given in the previous section.Using the continuous symmetry generators, the one-dimensional optimal algebra is obtained as: 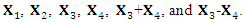 The discrete symmetry
The discrete symmetry 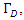 maps
maps 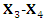 to
to 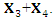 Thus, there is a reduction of number of elements of the optimal algebra [3].
Thus, there is a reduction of number of elements of the optimal algebra [3].
3. Exact Solutions
In this section exact solution of KdV equation, corresponding to each element of the optimal algebra, are obtained.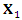 gives a constant function, i.e.
gives a constant function, i.e. 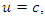 which is a trivial solution.The invariants for the generator
which is a trivial solution.The invariants for the generator 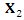 are
are 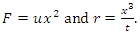 | (15) |
The invariant equation is 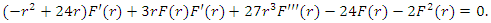 | (16) |
The solution of this invariant equation is 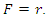 Therefore, the solution of the KdV equation is
Therefore, the solution of the KdV equation is 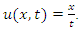 For
For 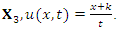 For
For 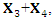 the invariants are
the invariants are 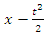 and
and 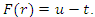 The KdV equation takes the form
The KdV equation takes the form 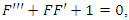 which is a third order nonlinear differential equation.
which is a third order nonlinear differential equation.
4. Symmetries of Nonlinear Filtration Equation
The motion of a non-Newtonian, weakly compressible fluid in a porous medium with a nonlinear filtration law 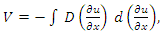 | (17) |
where 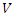 is the speed of filtration and
is the speed of filtration and 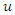 is the pressure is described by nonlinear filtration (NLF) equations [10,11]
is the pressure is described by nonlinear filtration (NLF) equations [10,11]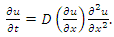 | (18) |
The function 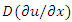 is known as filtration coefficient. In general the filtration coefficient is not fixed. NLF equations have been solved for various filtration coefficients [10,11].We choose
is known as filtration coefficient. In general the filtration coefficient is not fixed. NLF equations have been solved for various filtration coefficients [10,11].We choose 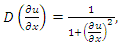 | (19) |
to find the discrete symmetries and group invariant solutions of this NLF equation which then lead to solutions under transformations due to the discrete symmetries.The infinitesimal generators of (one-parameter) Lie groups of point symmetries of the NLF equation are [12].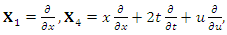 | (20) |
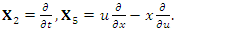 | (21) |
 | (22) |
Corresponding (one-parameter) Lie groups of point symmetries are 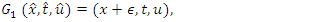 | (23) |
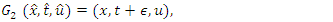 | (24) |
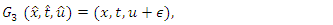 | (25) |
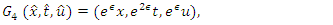 | (26) |
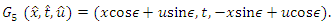 | (27) |
Using these symmetries in the technique mentioned in Section 1, following discrete symmetries of the nonlinear filtration equation are obtained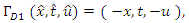 | (28) |
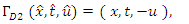 | (29) |
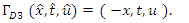 | (30) |
5. Exact Solutions
In this section an attempt has been made to find the group invariant solutions of the NLF equation due to the groups generated by 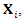 the basis generators. The group invariant solutions are then transformed using the discrete symmetries to obtain solutions.For
the basis generators. The group invariant solutions are then transformed using the discrete symmetries to obtain solutions.For 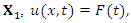 where
where 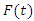 is invariant. On substituting it in NLF equation we have
is invariant. On substituting it in NLF equation we have 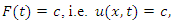 which is trivial solution.The symmetry generator
which is trivial solution.The symmetry generator 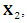 yields
yields 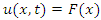 . We now substitute this solution in NLF equation to determine
. We now substitute this solution in NLF equation to determine 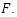 We obtain
We obtain 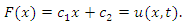 | (31) |
There does not exist any group invariant solutions due to 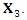 For
For 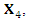 the invariants are
the invariants are 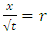 and
and 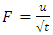 . Writing NLF equation interms of these invariants to determine
. Writing NLF equation interms of these invariants to determine 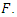
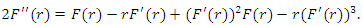 | (32) |
This is a second order nonlinear ODE for 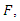 whose solution is
whose solution is 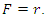 Hence,
Hence, 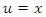 is the solution of the equation under consideration.For
is the solution of the equation under consideration.For 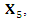 we have
we have 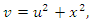 and
and 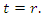 | (33) |
Therefore, we have 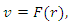 | (34) |
We now substitute this solution in NLF equation to obtain 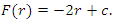 | (35) |
So 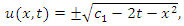 | (36) |
All these solutions are due to the continuous symmetries of the NLF equation. Using discrete symmetries one more solution 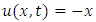 is also obtained.
is also obtained.
6. Conclusions
There is a lot of literature available on the applications of continuous symmetries, in particular, on finding solutions of ordinary and partial differential equations. In recent past, Peter E. Hydon introduced a technique to obtain discrete symmetries using continuous symmetries. These discrete symmetries are then used to obtain some new solutions that could not be obtained by only using continuous symmetries. In this paper, using both discrete and continuous symmetries of the Korteweg de Vries (7) and the nonlinear filtration equations, group invariant solutions and the exact solutions of these equations are presented.
References
| [1] | Hans Stephani, Malcolm MacCallum. Differential Equations: Their Solution using Symmetries, Cambridge University Press. 1989. |
| [2] | G. W. Bluman and S. Kumei. Symmetries and Differential Equations, Springer. 1989. |
| [3] | Peter J. Olver. Applications of Lie Groups to Differential Equations, Graduate Texts in Mathematics, 2nd Edition. 1993. |
| [4] | Fisher DJ, Gray RJ, Hydon PE. Automorphisms of real Lie algebras of dimension five or less, J. Phys. A: Math. Theor., 46: 225204. 2013. |
| [5] | Laine-Pearson FE, Hydon PE. Classification of matrices for discrete symmetries of ordinary differential equations, Stud. Appl. Math. 111: 269-299. 2003. |
| [6] | Hydon PE. Discrete point symmetries of ordinary differential equations, Proc. Roy. Soc. Lond. A 454: 1961-1972. 1998. |
| [7] | Hydon PE. How to use Lie symmetries to find discrete symmetries, Modern Group Analysis VII, eds N. H. Ibragimov, K. R. Naqvi, E. Straume, MARS Publishers, Trondheim, 141-147. 1999. |
| [8] | Hydon PE. How to construct the discrete symmetries of partial differential equations, Eur. J. Appl. Math. 11: 515-527. 2000. |
| [9] | Hydon PE. Discrete symmetries of differential equations, The Geometrical Study of Differential Equations, eds Joshua A. Leslie and Thierry P. Robart, American Mathematical Society, Providence, RI, 61-70. 2001. |
| [10] | I. SH. Akhatov, R. K. Gazizov, N. Ibragimov. Group Classification of the Equations of Nonlinear Filtration, Soviet Math. Dokl. Vol 35, No. 2. 1987. |
| [11] | Q. S. Abdul Aziz. Exact Solutions of Nonlinear Filtration Equation obtained by a Generalized Conditional Symmetry Method, Basrah Journal of Science (A), Vol 24 (2), 119-125. 2006. |
| [12] | Hydon PE. Symmetry Methods for Differential Equations: A Beginner’s Guide, Cambridge University Press, 1st Edition. 2000. |



 dimensional Lie algebra L of symmetries of differential equations. This gives a change in basis vectors and is represented as
dimensional Lie algebra L of symmetries of differential equations. This gives a change in basis vectors and is represented as 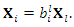
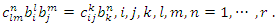
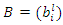 that corresponds to the automorphism. They fix some of the entries of matrix
that corresponds to the automorphism. They fix some of the entries of matrix 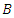 . The adjoint action of each basis vector,
. The adjoint action of each basis vector, 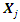 , generates a one-parameter Lie group of inner automorphisms whose matrix representation is [4]
, generates a one-parameter Lie group of inner automorphisms whose matrix representation is [4] 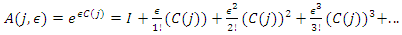
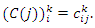
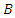 can be further simplified with the help of
can be further simplified with the help of 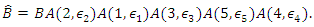
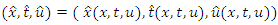
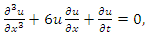
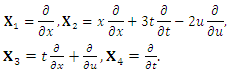
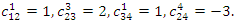
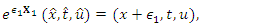
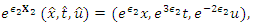
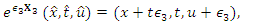
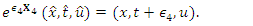
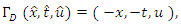
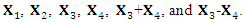 The discrete symmetry
The discrete symmetry 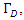 maps
maps 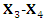 to
to 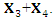 Thus, there is a reduction of number of elements of the optimal algebra [3].
Thus, there is a reduction of number of elements of the optimal algebra [3]. 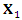 gives a constant function, i.e.
gives a constant function, i.e. 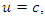 which is a trivial solution.The invariants for the generator
which is a trivial solution.The invariants for the generator 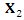 are
are 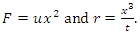
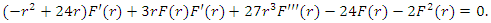
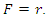 Therefore, the solution of the KdV equation is
Therefore, the solution of the KdV equation is 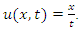 For
For 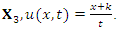 For
For 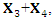 the invariants are
the invariants are 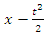 and
and 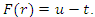 The KdV equation takes the form
The KdV equation takes the form 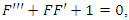 which is a third order nonlinear differential equation.
which is a third order nonlinear differential equation.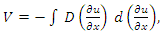
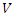 is the speed of filtration and
is the speed of filtration and 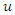 is the pressure is described by nonlinear filtration (NLF) equations [10,11]
is the pressure is described by nonlinear filtration (NLF) equations [10,11]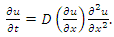
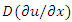 is known as filtration coefficient. In general the filtration coefficient is not fixed. NLF equations have been solved for various filtration coefficients [10,11].We choose
is known as filtration coefficient. In general the filtration coefficient is not fixed. NLF equations have been solved for various filtration coefficients [10,11].We choose 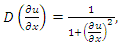
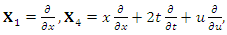
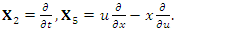

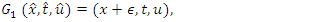
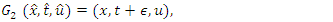
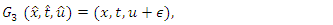
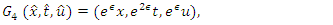
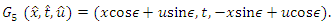
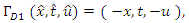
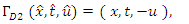
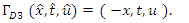
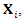 the basis generators. The group invariant solutions are then transformed using the discrete symmetries to obtain solutions.For
the basis generators. The group invariant solutions are then transformed using the discrete symmetries to obtain solutions.For 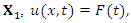 where
where 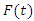 is invariant. On substituting it in NLF equation we have
is invariant. On substituting it in NLF equation we have 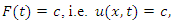 which is trivial solution.The symmetry generator
which is trivial solution.The symmetry generator 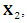 yields
yields 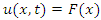 . We now substitute this solution in NLF equation to determine
. We now substitute this solution in NLF equation to determine 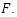 We obtain
We obtain 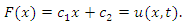
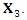 For
For 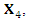 the invariants are
the invariants are 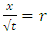 and
and 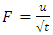 . Writing NLF equation interms of these invariants to determine
. Writing NLF equation interms of these invariants to determine 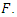
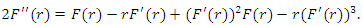
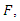 whose solution is
whose solution is 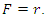 Hence,
Hence, 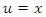 is the solution of the equation under consideration.For
is the solution of the equation under consideration.For 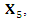 we have
we have 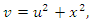 and
and 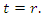
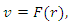
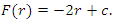
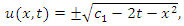
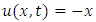 is also obtained.
is also obtained. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML