1. Introduction

The safety and reliability of large infrastructure such as aircraft, high-speed trains and ships have always been the focus of social concern. In these large facility projects, alloys often play an important role as key components. For example, in the aero-engine, superalloy materials are usually used in the combustion chamber, turbine disc, turbine blade and other core components, accounting for about 40%~60% of the total material of the engine. However, residual stress is inevitably introduced in the process of mechanical manufacturing, machining and surface treatment of components [1,2]. In the actual service environment, the introduced residual stress will evolve further. The existence and evolution of residual stress directly affect the properties of materials or components, and then threaten the safety of life and property [3,4]. Therefore, it is of great significance to accurately measure the residual stress of engineering materials.

The traditional residual stress measurement methods can be roughly divided into mechanical stress relaxation method and physical parameter analysis method. Among them, the mechanical stress relaxation method is generally used to release part of the residual stress in the material, measure the deformation caused by the change of the residual stress, and then calculate the residual stress [5-8]. The mechanical stress relaxation method includes drilling, slitting and cutting of ring core. However, these methods are disruptive and limit the wide use of these techniques in industry. Physical parameter analysis methods, including X-ray diffraction, neutron diffraction, ultrasonic and magnetic Barkhausen noise, can be used to measure the residual stress through the essential properties of materials and nondestructive measurement, and some methods have been partially applied in the industrial field [9-11]. However, these physical methods are limited by the inherent microstructure of the material, and it is necessary to prepare stress-free samples for reference. In addition, X-ray diffraction and neutron diffraction methods cannot be applied directly to amorphous materials because they do not have long-range ordered atomic structures.

The instrumented indentation method (IIT) is another promising technique for measuring surface residual stress, which has high displacement and load resolution, and can continuously record the changes of load and displacement during indentation contact. Due to its small indentation range, the components under real service conditions can be detected with non-destructive in real-time. Great efforts have been made to investigate the influence of residual stress on the measurement of mechanical properties using instrumented indentation. In 1996, the influence of the surface residual stress on the results obtained using indentation testing was first investigated by Boshakov and Oliver et al [12,13]. Through experimental observations and finite element analysis, they found that the existence of residual stress had an effect on the contact area at the same depth of indentation, but had a minimum effect on hardness. In order to further study the effects of residual stress on the contact area, Suresh and Giannakopoulos proposed a theoretical model for the determination of the surface residual stresses based on a sharp indentation in 1998 [14]. In 2001, Carlsson and Larsson suggested a correlation between the equi-biaxial residual stress and the size of the contact area [15,16]. Subsequently, Lee et al. investigated the load difference between stressed and unstressed specimens at the same indentation depth to estimate residual stress [17,18]. In 2006, Xu et al. systematically studied the influence of residual stress on the elastic recovery of nano-indentation through a large number of finite element simulations and found that the residual stress not only affected the real contact area but also affected the elastic recovery ratio. Similarly, Carlsson and Lee agree that the contact area ratio in the determination of residual stress was useful. However, it is difficult to measure the contact area directly during indentation tests. To solve this problem, Zhao et al. proposed a method to determine the residual stress of materials based on the load-displacement curves recorded during the indentation process. This method does not need to measure the contact area, but its limitation is that it is only suitable for ideal elastoplastic materials, and a large number of empirical coefficients need to be obtained. All the methods mentioned above are based on the theoretical model of Oliver–Pharr method to obtain material parameters [19].

Apart from sharp indenter, a blunt spherical indentation for measuring the residual stress can be used. Taljat and Pharr suggested that spherical indentation is more sensitive to stress effects than sharp indentation through theoretical predictions and finite element analyses [20]. They found that residual stresses have a significant effect on the indentation load-displacement curves in the elastic-plastic transition regime. Subsequently, Swander et al. proposed two methods of determining equi-biaxial residual stresses via spherical indentation based on the discovery of Taljat and Pharr [21]. However, the limitation of spherical indentation is that the yield strength of the material needs to be known in advance and the actual contact area needs to be measured. To solve this weakness, Peng et al. proposed a method to estimate the equi-biaxial residual stress and elastic-plastic parameters of metals simultaneously via instrumented spherical indentation which can avoid preknowledge of the yield strength and measuring the contact area [22].

Recently, through theoretical analysis and finite element simulation, Liu and Shen et al. found that the pile-up morphology around the indentation after unloading can be associated with the direction of surface residual stress and the amount of pile-up is dependent on the magnitude of surface residual stress [23,24]. The greatest advantage of this method is that the pile-up height generated in the experiment can be easily measured. Additionally, some researchers have extended the indentation method to nonmetallic materials. The effect of the internal microstructure especially the pores on mechanical properties of plasma-sprayed coatings using sharp indentation was investigated by Qiao et al [25]. Akahori et al. proposed a method for evaluating the residual stress of polymeric materials using spherical indentation tests.

In general, the Oliver-Pharr method is the most widely used method for measuring material parameters and residual stress in current research [19]. However, when using the Oliver-Pharr method, the main problem is how to calculate the actual contact area. At present, there have been some studies on how to calculate the contact area or the influence of avoiding the contact area [22,26]. In addition, spherical indentation is more sensitive to stress effect than sharp indentation, but the specific value of the difference needs to be further studied. Some researchers pointed out that when calculating the residual stress of soft materials, the error margin of the results obtained by the Suresh model and Lee model would be relatively large, which might not be applicable to the calculation [27]. In addition, it seems more intuitive to characterize the residual stress through the packing morphology. However, previous studies on the packing morphology are mostly based on finite element analysis and lack of experimental verification. Therefore, it is necessary to judge whether the method based on the packing morphology is accurate.

In this paper, the experimental test platform were established to generate the pile-up morphology first. Then, the relationship between residual stress and pile-up morphology was studied by experimental investigation. Finally, the experimental results verify the accuracy of the method based on spherical indentation of the pile-up morphology.

2. Experimental Procedure

This study used a Brinell hardness tester as an indentation equipment (HBE-3000M) to investigate the relationship between pile-up morphology and residual stress. A spherical indenter was used, as shown in Fig. 1 (a). The indentation equipment has 12 loading load presets in the loading range 62.5-3000 kgf, equipped with a rigid spherical indenter with a diameter of 1 mm, 2.5mm, 5mm, and 10mm, respectively. The indenter of 2.5 mm diameter was selected for this experiment. As shown in Fig. 1 (b), the white light interferometer (Filmetricsinc, Profilm3D) was used to obtain the pile-up morphology after indentation unloading and to extract its maximum pile-up height. The equipment test accuracy is 0.01μm, which meets the accuracy requirements for this experiment.

Figure 1. Experimental setup

The specimen used in this study was aluminum 2024 (2024 Al), which is prone to pile-up and easy to purchase. In this study, several 2024 Al specimens prepared with different residual stress preconditions. A four-point bending fixture was designed to apply tensile or compressive stress to the specimen, as shown in Fig. 2. Accordingly, the specimen suitable for the fixture was cross-shaped and had dimensions of 105 mm length, 25 mm width, and 3 mm thickness. During the experiment, the residual stress was introduced by controlling the screwing of four bolts, as shown in Fig. 3. It is worth noting that the process of specimen loading at four-point bending will undergo bending deformation to produce bending stress, and then form tensile and compressive stress on the upper and lower surfaces of the specimen, respectively. By using strain gauges, the applied stress can be determined by observing the strain according to the stress-strain relationship as shown in Equation 1.

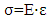(1)

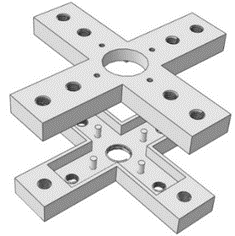Figure 2. 3D schematic diagram of residual stress application fixture

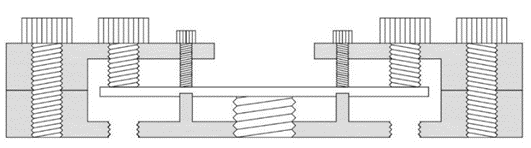Figure 3. Schematic diagram of stress application fixture

3. Results and Discussions

Finite element simulation (ABAQUS 6.14) was used to simulate and analyze the loading condition of the specimen in the experiment to ensure that the stress applied on the material surface by the loading device is in the expected stress state, in which the simulation results of the equi-biaxial stress state are shown in Fig. 4. The S11 and S22 stress contours generated on the surface of the specimen are the same after simulating the application of 100 MPa of equi-biaxial stress, which indicates that uniform equi-biaxial stress was generated inside the specimen. Fig. 5 shows the stress contour of the simulated specimen after applying 100 MPa and 50 MPa stress respectively. In the figure, the amount of S11 and S22 stress contour on the surface of the specimen are twice different, indicating that the non-equi-biaxial stress as expected was generated inside the specimen.

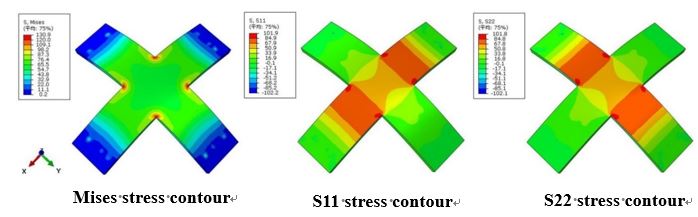Figure 4. Stress contour of equi-biaxial stress

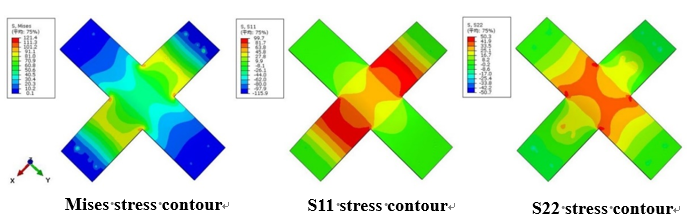Figure 5. Stress contour of non-equi-biaxial stress

When the stress loading was completed, the indenter was indented into the center area in the cross-shaped specimen and unloaded after 15 seconds of load holding. Finally, the specimen can generate the pile-up morphology near the indentation point and the maximum pile-up height can be obtained by the white light interferometer.

In this investigation, the compressive stress of 75 MPa was fixed in one direction while the stress in another direction varied in the range of -75~75 MPa. It is should be pointed out that the minus sign indicates compression.

According to the experimental method in section 2, the non-equivalent biaxial stress was applied to the cross-shaped specimen. After the indentation was unloaded, the white light interferometer was used to scan the morphology to obtain the surface pile-up morphology.

Fig. 6 shows the surface morphology obtained by scanning the surface morphology of the specimen (σx=-75MPa and σy=75MPa) using the white light interferometer. As can be seen from the figure that the morphology obtained by scanning the specimen under the condition of non-equi-biaxial stress shown the obvious pile-up phenomenon, and the position of the maximum pile-up height and the change trend of the pile-up morphology can be seen intuitively on the figure.

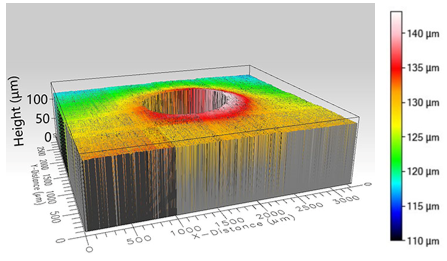Figure 6. Morphology near the indentation (σx =-75MPa and σy=75MPa)

Based on the obtained full-field morphology [23,24], the morphology near the indentation point is further analyzed to determine the main direction of the applied stress and its maximum pile-up height. To determine the main direction of the applied stress conveniently, the polar coordinate system was established with the indentation point as the coordinate origin, where the x-axis is taken as the starting direction and the angle α represented the direction of the extracted radial path. Starting from the coordinate origin, set the path as shown in the blue line segment in the figure along different angle α and extract its maximum pile-up height, as shown in Fig. 7.

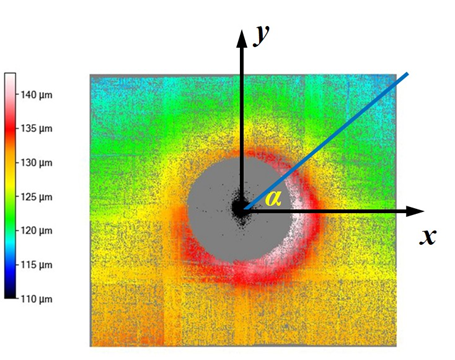Figure 7. The schematic diagram of the established polar coordinate system

The full-field pile-up morphology in Fig. 7 was extracted along with the established polar coordinate system for the maximum pile-up height on the radial path corresponding to different angles, and the results were shown in Fig. 8. The black spot shown in Fig. 8 are the maximum pile-up height in each extracted radial direction. It is worth noting that the effect of the specimen roughness and the errors generated in the measurement process together cause irregular changes such as the fluctuation of the data in some areas in the figure. To reduce the error of the data, the fast Fourier transform (FFT) fitting of the original data was performed to eliminate the noise points, and then the quadratic interpolation is carried out. The results are shown in the red data points in Fig. 8.

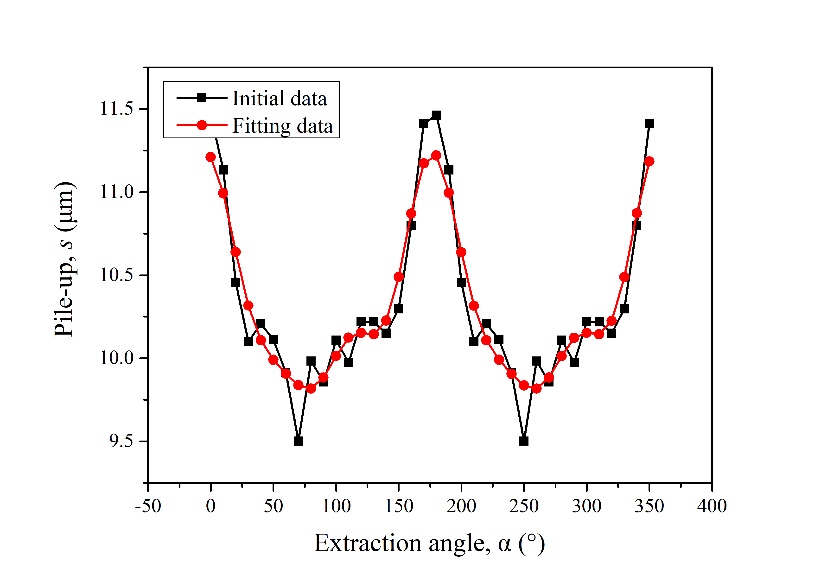Figure 8. Distribution diagram of maximum pile-up height (σx =-75MPa σy=75MPa)

It can be seen from the fitting curve that the maximum pile-up height near the indentation point shows a trend of decreasing initially and then increasing. Besides, there are two peak points and two valley points in Fig. 8, and the peak points represent the direction of compressive stress and the valley points represent the direction of tensile stress. The peak points in figure occurred at 0° (180°), and the magnitude is 11.46 μm, while the valley value occurred at 90° (270°), and the magnitude is 9.86 μm. Thus, the peak and valley points on the curve can be preliminarily inferred to help determine the direction of the applied stress.

Similarly, the pile-up morphology under uniaxial compression and uniaxial tensile stress was extracted and analyzed, and the corresponding maximum pile-up height distribution diagram was drawn, as shown in Fig. 9.

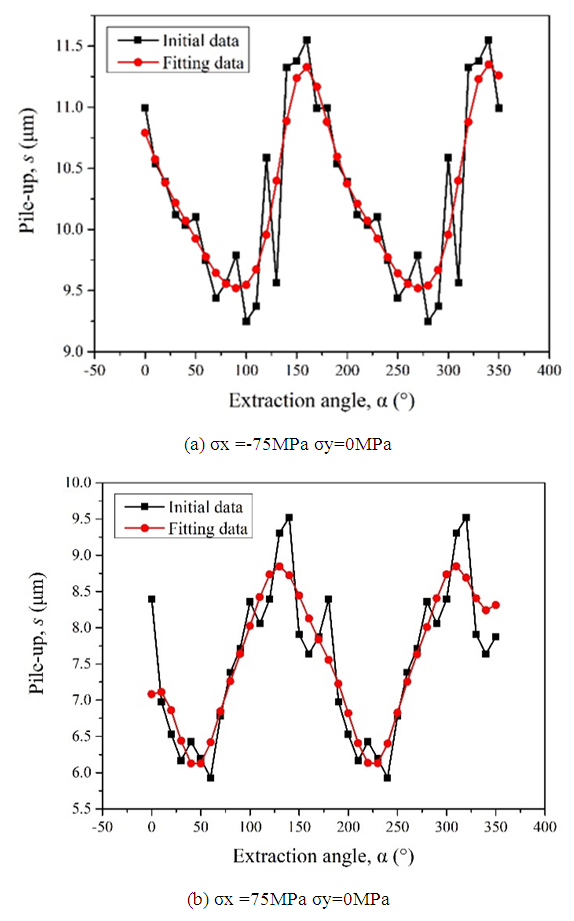Figure 9. Distribution diagram of maximum pile-up height

The variation curve of pile-up height shown in Fig. 9 showing the trend of sinusoidal change, consistent with the finite element simulation results as shown in Fig. 10, which indicates that the experimental results are reliable. Besides, the corresponding direction of the peak points and the valley points of the curve in Fig. 9 should be the main direction of stress application. Thus, the stress direction can be directly determined by the peak points and valley points in the maximum pile-up height distribution diagram near the indentation point.

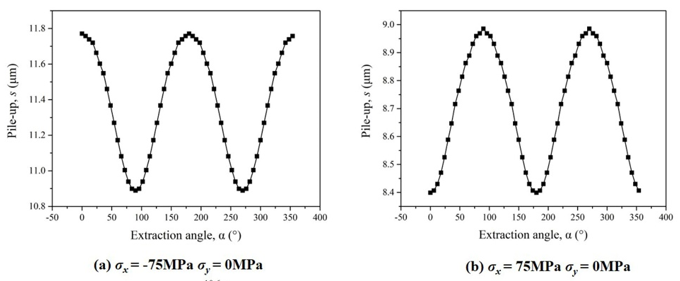Figure 10. Finite element simulation results of maximum pile-up height

Surface morphology was measured in seven groups of indentation experiments, and FFT fitting was performed. Then, the stress direction was determined according to the maximum pile-up height distribution diagram, and the maximum pile-up height in the stress direction was extracted, as shown in Fig. 11.

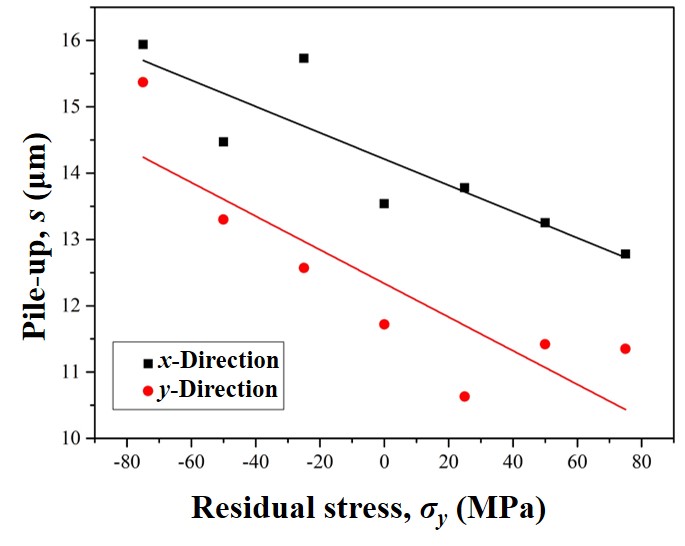Figure 11. Schematic diagram of a variation of maximum pile-up height with residual stress

According to Fig. 11, as the stress in the y-direction changes from the compressive stress state to the tensile stress state, both the maximum pile-up height in the x-direction and y-direction show a trend of gradual decrease. This is since tensile stress will reduce the pile-up height while compressive stress will increase the pile-up height. Also, it can be found that the reduction velocity of pile-up height in the x-direction is smaller than that in the y-direction, because the y-direction is the main direction of stress change, so it is more sensitive to stress change.

4. Conclusions

In this paper, based on the method proposed by Shen et al., the method of measuring the residual stress by the indentation method is systematically and deeply studied with experiment. The experimental results show that the change curve of the stacking height presents a sinusoidal trend, and the direction corresponding to the peak and valley points of the curve is the main direction of stress application. Therefore, the direction of stress can be directly determined by the peak and valley points in the distribution map of the maximum packing height near the indentation point. Besides, as the stress in the y-direction changes from the compressive stress state to the tensile stress state, both the maximum pile-up height in the x-direction and y-direction show a trend of gradual decrease. Also, it can be found that the reduction velocity of pile-up height in the x-direction is smaller than that in the y-direction, because the y-direction is the main direction of stress change, so it is more sensitive to stress change.