Andrey Yelyseiovych Babenko1, Babak Soltannia2, Pouyan Shakeri Mobarakeh3
1Department of Mechanical Engineering, National Technical University of Ukraine, Igor Sikorsky Kyiv Polytechnic Institute, 37 Peremogy Avenue, Kyiv, Ukraine
2Department of Mechanical Engineering, University of Alberta, 10-203 Donadeo Innovation Centre for Engineering, Alberta, T6G 1H9, Canada
3Department of Theoretical and Applied Mechanics, Faculty of Mechanics and Mathematics, Kiev National Taras Shevchenko University, Kiev, Ukraine
Correspondence to: Babak Soltannia, Department of Mechanical Engineering, University of Alberta, 10-203 Donadeo Innovation Centre for Engineering, Alberta, T6G 1H9, Canada.
| Email: |  |
Copyright © 2018 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
Deformation of the helical springs is mostly considered as linear, due to their linearly proportionate elongation to their applied load. However, this assumption is not capable of capturing the full and accurate mechanical behavior of helical springs undergoing large deformations. Moreover, their mechanical behavior under compression is usually neglected. In this article, the problem of the tension-compression of a helical spring is solved with higher accuracy by considering a modification of its geometrical parameters. The novel solution, based on the use of variational methods, is both precise and much easier to apply than a solution based on the use of differential equations.
Keywords:
Geometrically Nonlinear, Nonlinear Spring, Helical Spring, Large Deformation, Nonlinear Deformation, Variational Methods
Cite this paper: Andrey Yelyseiovych Babenko, Babak Soltannia, Pouyan Shakeri Mobarakeh, Solving Geometrically Nonlinear Problem on Deformation of a Helical Spring through Variational Methods, International Journal of Mechanics and Applications, Vol. 8 No. 1, 2018, pp. 21-24. doi: 10.5923/j.mechanics.20180801.03.
1. Introduction
Springs are essential components of many devices and machines. They can be used as damping element in a mechanical system to minimize vibration or impact. Nowadays, they are necessary components used in automotive, train, and aerospace industries [1, 2]. Spring behavior can be also used to model different materials such as polymer composites, or metals [3-5]. Spring failure due to forced vibration also needs to be addressed [6, 7]. To accurately model these materials, or to better optimize the mechanical system containing spring element, and to augment the efficiency, it is essential to account for nonlinearity of the springs [8-10], and propose a constitutive model which accounts for both contraction and extension of springs [11-13]. In this article, the problem of the tension-compression of a helical spring is solved with higher accuracy by considering a modification of its geometrical parameters. The novel solution, based on the use of variational methods, is both precise and much easier to apply than a solution based on the use of differential equations.Here, we consider a geometrically nonlinear problem. Since the rod, in this case, is flexible, the impact of axial forces N and transverse forces Q is small compared to the bending moment 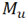 and twisting moment
and twisting moment 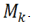 Hence, the axial force N and transverse force Q are not taken into account.The axial line is a helix, and its radius-vector in the Cartesian coordinate system is described by the equation
Hence, the axial force N and transverse force Q are not taken into account.The axial line is a helix, and its radius-vector in the Cartesian coordinate system is described by the equation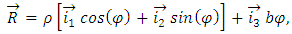 | (1) |
where φ is the parameter that represents the angle, ρ is the cylinder radius, and 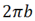 is the pitch of a spring. On the other hand, a helix line, as for any curve, is defined by setting the curvature k and twist
is the pitch of a spring. On the other hand, a helix line, as for any curve, is defined by setting the curvature k and twist 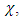 linked to ρ and b correlations:
linked to ρ and b correlations: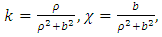 | (2) |
Hence, their inverse relationships have the following forms: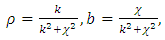 | (3) |
Furthermore, the tangent vector to the helix line is determined by the first derivative of the radius vector under the parameter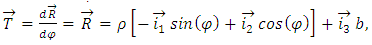 | (4) |
and its length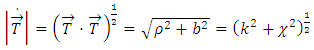 | (5) |
If we select a natural parameter as the parameter (which is the length of the arc S), then by using (5), we can obtain the natural parameter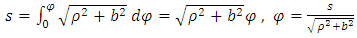 | (6) |
From (4) and (6), we can then obtain the radius-vector 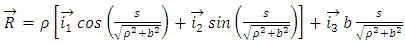 | (7) |
Since, in accordance with the statement of the problem, the rod elongation is not taken into account, the length of the rod remains unchanged and equal to L. To determine the spring length, we find the radius-vector for the farthest point at s = L. The spring compression λ is equal to the difference between the radius-vector projections on the axis of the spring in both initial and final states, such that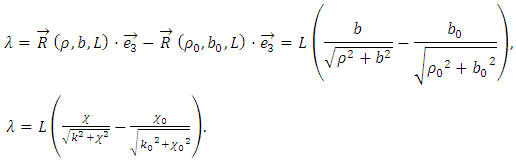 | (8) |
Because we are considering a physically linear problem, the bending moment 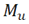 and twisting moment
and twisting moment 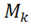 are proportional to the change of the curvature and torsion, respectively. If the initial curvature of the rod (wire) is
are proportional to the change of the curvature and torsion, respectively. If the initial curvature of the rod (wire) is 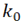 and its torsion (twist) is
and its torsion (twist) is 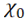 , we have
, we have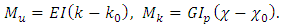 | (9) |
Hence, the strain potential energy, just considering bending moment and torsion, can be calculated as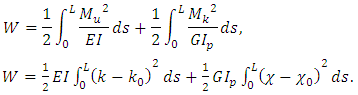 | (10) |
If we consider the helical spring with the free ends under axially symmetric load, its curvature and twist are constant along its length. Under these conditions, 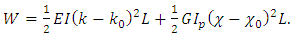 | (11) |
In accordance with the principle of virtual work, the sum of the works by external and internal forces on the possible displacements is zero. This condition is equivalent to the condition where the sum of the variation work of external forces and strain energy is zero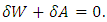 | (12) |
The variation of strain potential energy is equal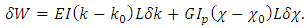 | (13) |
A variation of the work in the result of external forces is 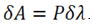 Since the variation of the movement of the points under the applied load is equal to the variation of the spring compression,
Since the variation of the movement of the points under the applied load is equal to the variation of the spring compression,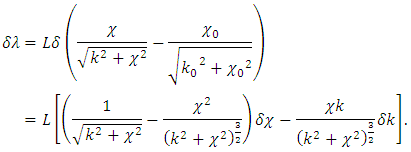 Therefore,
Therefore,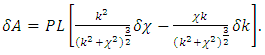 | (14) |
Considering (12), (13) and (14), we obtain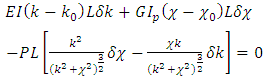 | (15) |
By regrouping components containing variations and taking into account that the variation of curvature and torsion are arbitrary, to satisfy Equation (15) it requires to cancel out (nullify) the coefficients behind variations. Therefore, we obtain the equations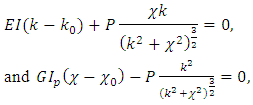 | (16) |
The obtained equations (16) allow us to exclude the force P. Furthermore, by using correlations 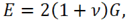
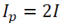 for the circular rod, we can find the relation between the twist and the curvature:
for the circular rod, we can find the relation between the twist and the curvature: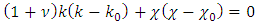 | (17) |
By expressing the torsion and bending through the radius and the pitch of spring, in accordance with (2), we get: 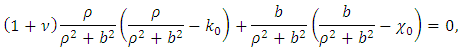 Then, by expressing the pitch through the radius and elevation angle of the helix line, we can calculate:
Then, by expressing the pitch through the radius and elevation angle of the helix line, we can calculate: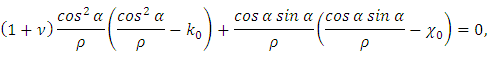 and thus obtain a formula for easily determining the spring strain
and thus obtain a formula for easily determining the spring strain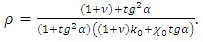 | (18) |
2. Result and Discussion
Figures 1 to 5 show the results of the spring deformation with the following parameters: Young's modulus 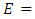
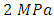 ; Poisson's ratio
; Poisson's ratio 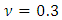 ; wire (rod) diameter
; wire (rod) diameter 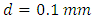 ; the mean radius of the cylinder (coil)
; the mean radius of the cylinder (coil) 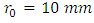 ; the initial value of the parameter determining pitch
; the initial value of the parameter determining pitch 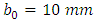 ; and the initial value corresponding to the initial curvature
; and the initial value corresponding to the initial curvature 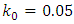 , the initial torsion
, the initial torsion 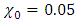 , and the initial elevation angle
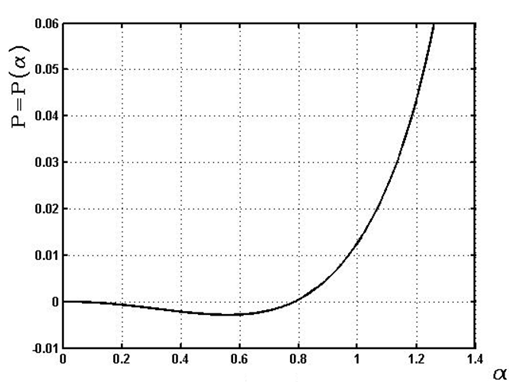
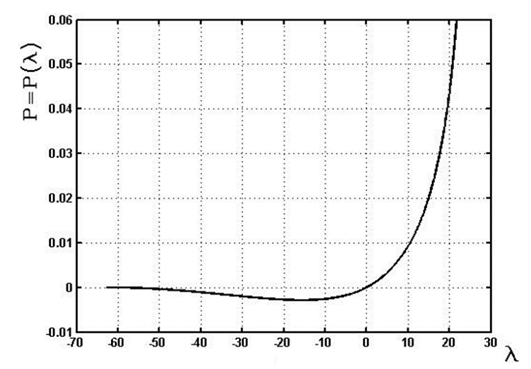
, and the initial elevation angle 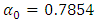 .This example has the typical feature of a large spring pitch. The calculated results show that the single relationship between the radius and elevation angle is close to linear as it is shown in Figure 2, whereas all other parameters are far from linear. Furthermore, the relationship between force and displacement (Figure 5) is negative under compression, which is the main reason for instability. The derived formulas can be used to calculate long multi-turn springs, with negligible boundary condition effects. When considering short springs, we need to consider the boundary conditions.
.This example has the typical feature of a large spring pitch. The calculated results show that the single relationship between the radius and elevation angle is close to linear as it is shown in Figure 2, whereas all other parameters are far from linear. Furthermore, the relationship between force and displacement (Figure 5) is negative under compression, which is the main reason for instability. The derived formulas can be used to calculate long multi-turn springs, with negligible boundary condition effects. When considering short springs, we need to consider the boundary conditions.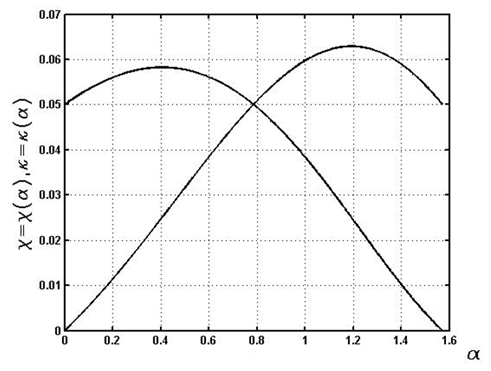 | Figure 1 |
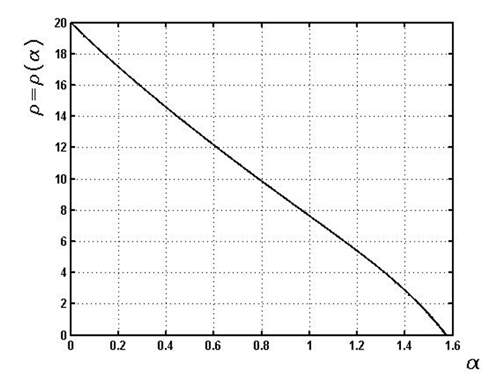 | Figure 2 |
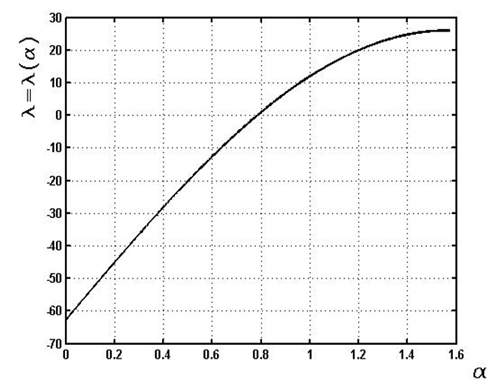 | Figure 3 |
 | Figure 4 |
 | Figure 5 |
3. Conclusions
In contrast to many cases, were deformation of the helical springs is considered as linear, due to their linearly proportionate elongation to their applied load, as well as neglecting its behavior under compression, in this work we achieved the full picture of spring’s mechanical behavior undergoing large deformation, accounting for nonlinearity, and contraction. It was shown that the solution based on variational principle, is both precise and much easier to apply than a solution based on the use of differential equations.
References
| [1] | G. Bhimrao Jadhav, V. Gawande, Review on Development and Analysis of Helical Spring with Combination of Conventional and Composite Materials, Int. J. Eng. Res. Gen. Sci. 3 (n.d.). |
| [2] | Y. Kara, A Review: Fiber Reinforced Polymer Composite Helical Springs, J Mater Sci Nanotechnol. 5 (2017) 101. doi:10.15744/2348-9812.5.101. |
| [3] | T.S. Manjunatha, D. Abdul Budan, Manufacturing and Experimentation of Composite Helical Springs for Automotive Suspension, 2012. |
| [4] | M. Bakhshesh, M. Bakhshesh, Optimization of Steel Helical Spring by Composite Spring, Int. J. Multidiscip. Sci. Eng. 3 (2012) 47–51. |
| [5] | C.-H. Chiu, C.-L. Hwan, H.-S. Tsai, W.-P. Lee, An experimental investigation into the mechanical behaviors of helical composite springs, Compos. Struct. 77 (2007) 331–340. doi:10.1016/J.COMPSTRUCT.2005.07.022. |
| [6] | G. Vukelic, M. Brcic, Failure analysis of a motor vehicle coil spring, Procedia Struct. Integr. 2 (2016) 2944–2950. doi:10.1016/j.prostr.2016.06.368. |
| [7] | E. Sancaktar, S. Gowrishankar, Natural Frequencies of Composite Cylindrical Helical Springs Manufactured Using Filament Winding, in: 2009. |
| [8] | A. Love, A treatise on the mathematical theory of elasticity, Cambridge: At The University Press., 1892. |
| [9] | G.R. Kirchhoff, Vorlesungen über mathematische Physik. Mechanik, Leipzig, 1876. |
| [10] | I.N. Bronstein, K.A. Semendyayev, G. Musiol, H. Muehlig, Handbook of Mathematics, Fifth, Springer Berlin Heidelberg, Berlin, Heidelberg, 2007. doi:10.1007/978-3-540-72122-2. |
| [11] | V. Faires, Design of machine elements., 4th ed., Macmillan, New York, 1965. |
| [12] | Society of Automotive Engineers. Spring Committee., Spring design manual, Society of Automotive Engineers, 1996. |
| [13] | A.M. Wahl, Mechanical springs / A.M. Wahl, 2nd ed., McGraw-Hill, New York, 1963. |



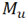 and twisting moment
and twisting moment 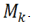 Hence, the axial force N and transverse force Q are not taken into account.The axial line is a helix, and its radius-vector in the Cartesian coordinate system is described by the equation
Hence, the axial force N and transverse force Q are not taken into account.The axial line is a helix, and its radius-vector in the Cartesian coordinate system is described by the equation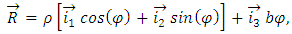
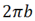 is the pitch of a spring. On the other hand, a helix line, as for any curve, is defined by setting the curvature k and twist
is the pitch of a spring. On the other hand, a helix line, as for any curve, is defined by setting the curvature k and twist 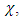 linked to ρ and b correlations:
linked to ρ and b correlations: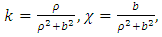
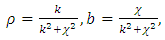
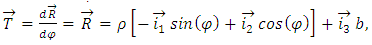
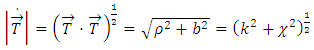
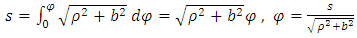
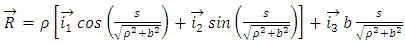
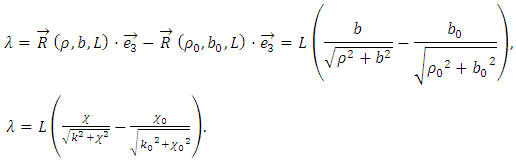
 and twisting moment
and twisting moment  are proportional to the change of the curvature and torsion, respectively. If the initial curvature of the rod (wire) is
are proportional to the change of the curvature and torsion, respectively. If the initial curvature of the rod (wire) is 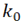 and its torsion (twist) is
and its torsion (twist) is 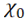 , we have
, we have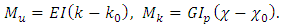
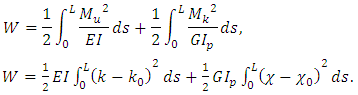
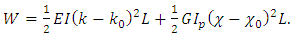
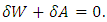
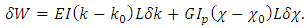
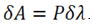 Since the variation of the movement of the points under the applied load is equal to the variation of the spring compression,
Since the variation of the movement of the points under the applied load is equal to the variation of the spring compression,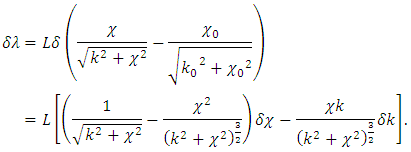 Therefore,
Therefore,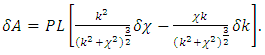
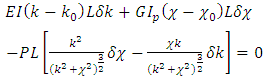
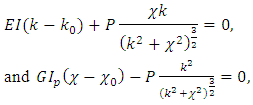
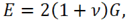
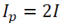 for the circular rod, we can find the relation between the twist and the curvature:
for the circular rod, we can find the relation between the twist and the curvature: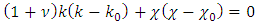
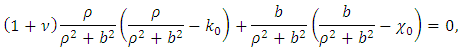 Then, by expressing the pitch through the radius and elevation angle of the helix line, we can calculate:
Then, by expressing the pitch through the radius and elevation angle of the helix line, we can calculate: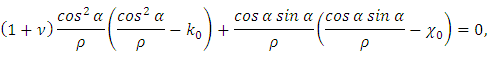 and thus obtain a formula for easily determining the spring strain
and thus obtain a formula for easily determining the spring strain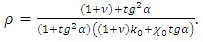
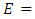
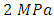 ; Poisson's ratio
; Poisson's ratio 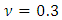 ; wire (rod) diameter
; wire (rod) diameter 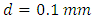 ; the mean radius of the cylinder (coil)
; the mean radius of the cylinder (coil) 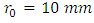 ; the initial value of the parameter determining pitch
; the initial value of the parameter determining pitch 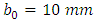 ; and the initial value corresponding to the initial curvature
; and the initial value corresponding to the initial curvature 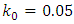 , the initial torsion
, the initial torsion 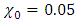 , and the initial elevation angle
, and the initial elevation angle 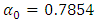 .This example has the typical feature of a large spring pitch. The calculated results show that the single relationship between the radius and elevation angle is close to linear as it is shown in Figure 2, whereas all other parameters are far from linear. Furthermore, the relationship between force and displacement (Figure 5) is negative under compression, which is the main reason for instability. The derived formulas can be used to calculate long multi-turn springs, with negligible boundary condition effects. When considering short springs, we need to consider the boundary conditions.
.This example has the typical feature of a large spring pitch. The calculated results show that the single relationship between the radius and elevation angle is close to linear as it is shown in Figure 2, whereas all other parameters are far from linear. Furthermore, the relationship between force and displacement (Figure 5) is negative under compression, which is the main reason for instability. The derived formulas can be used to calculate long multi-turn springs, with negligible boundary condition effects. When considering short springs, we need to consider the boundary conditions.




 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML