-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Mechanics and Applications
p-ISSN: 2165-9281 e-ISSN: 2165-9303
2018; 8(1): 1-9
doi:10.5923/j.mechanics.20180801.01

Unstable In-Plane Buckling Configurations of Beams on Elastic Unilateral Subgrade via Catastrophe Theory
Vasiliki S. Pantazi, Dimitrios S. Sophianopoulos
Department of Civil Engineering, University of Thessaly, Volos, Greece
Correspondence to: Dimitrios S. Sophianopoulos, Department of Civil Engineering, University of Thessaly, Volos, Greece.
| Email: |  |
Copyright © 2018 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Unstable equilibria associated with the nonlinear in-plane stability of an axially compressed simply supported inextensional Euler-Bernoulli beam resting on a tensionless unilateral Winkler (linear) foundation is dealt with in this work. The proposed approach is based on the construction of the system’s total potential energy and its exploration via Catastrophe Theory. The three-parameter singularity associated with the problem yields a special reduced type of the Butterfly Catastrophe, by evaluating the Bifurcation Set through successive eliminations. It represents a family of parameterized surfaces, which properly reconstructed show great resemblance to Swallowtail-like sections of the Butterfly Catastrophe. The unstable configurations, associated with one part of the beam in contact and the rest with no contact, are well captured and the corresponding critical buckling loads are established. The results obtained are found in good agreement with ones from two alternative approaches. Possible bifurcations prior to stable buckling as well as sudden jumps between classical Euler in- and out-of-plane buckling and the unbonded contact one are reported (a feature of the Cuspoids, including the Butterfly Singularity). Such undesirable phenomena have also been reported for nonlinear bilateral subgrade models.
Keywords: Buckling, Unstable configurations, Elastic foundation, Unbonded contact, Catastrophe theory, Singularities, Sudden jumps
Cite this paper: Vasiliki S. Pantazi, Dimitrios S. Sophianopoulos, Unstable In-Plane Buckling Configurations of Beams on Elastic Unilateral Subgrade via Catastrophe Theory, International Journal of Mechanics and Applications, Vol. 8 No. 1, 2018, pp. 1-9. doi: 10.5923/j.mechanics.20180801.01.
Article Outline
1. Introduction
- The buckling and postbuckling response of beams/struts (of either infinite or finite length) on elastic foundation has been the subject of a huge number of publications over the last 50 years, which were based on various linear as well as nonlinear subgrade models [1-3]. Even a limited reference of all these investigations lies beyond the scope of the present work. This simple structural component can rather easily simulate the stability response related to practical problems of various disciplines. Among these, one may quote the lateral thermal buckling of railway tracks [4], the stability of the top chord of low (pony) truss bridges [5], the mechanical response of metallic aortic stents [6] etc. Other theoretical approaches have also been reported [7-9], which however did not consider any underlying physical problem.The overwhelming majority of the works cited above (and of numerous others not referenced here for brevity) was based on the assumption that the subgrade is always in contact with the supported structure (bilateral), i.e. that the foundation always reacts, either in tension or in compression.However, the simple ideal beam only in axial compression resting on an elastic foundation may also model practical applications, in which the subgrade is of the so-called one-way, i.e. tensionless, of unilateral type. In such situations, a separation between parts of the beam and the foundation may occur, and hence the relevant problem is a discontinuous – unbonded contact one. Such a phenomenon has been reported in the literature, but in a limited number of works. For instance, in an earlier paper [10], Yun and Kyriakides simulated the “beam-mode buckling” exhibited by buried pipelines in compression (where a section of the line lifts through the ground), adopting a tensionless Winkler foundation. Later, Silveira et al. [11] studied – among other types of structures – the response of a simply supported beam acted upon simultaneously by end moments and a compressive axial force, resting on a Winkler tensionless foundation. The authors used a semi-analytical methodology via a Ritz type approach, which led to the determination of the contact and no contact region between beam and subgrade.Moreover, Battiprolu et al. [12, 13] in order to simulate the response of a pinned-pinned beam interacting with polyurethane foam foundation, adopted a beam-model on a nonlinear tensionless viscoelastic subgrade under axial compression and distributed as well as concentrated transverse loading. They also investigated the effect of various parameters, such as the relative foundation-beam stiffness, nonlinearities etc. Separation between beam and subgrade was evident also in this case.Finally, in a very recent paper [14], Ioakimidis derived the conditions of complete contact for a beam on a tensionless Winkler foundation, using symbolic computations available in modern quantifier elimination software [Mathematica, [15]]. In this study, the case of pure axial compression was considered, and as stated, the adopted subgrade model is frequently actually the case in practice.To this end, when the above described simple beam-model lacks imperfections and lateral restrictions, if it is loaded by a pure axial compressive force, only four (4) postbuckling deformation patterns may occur, as the load gradually increases from zero. Namely, the 1st one (abbreviated in what follows by PB1) is associated with the in-plane buckling “away” from the foundation (full separation – no contact at all), that is realized by the 1st Euler stable buckling mode in a single semi-wave form, with well-known properties. The 2nd pattern (PB2), out-of-plane Euler buckling in any mode, also stable, may as well occur but is not affected by the presence of the subgrade (friction neglected). The corresponding critical loads may be greater of small than the ones of the 1st pattern, depending on the beam’s properties and cross-section orientation. The 3rd simplest possible postbuckling configuration (PB3) is related to a single wave-form-like deformed shape in full contact with the subgrade, i.e. the whole beam is deflected inside the foundation. This will be possible only for certain combinations of the beam and foundation parameters [5, 14, 16-17] and the critical load may also be smaller or greater than the ones of PB1 and PB2. The last pattern (PB4) includes discontinuous contact, with yet unknown in number and length consecutive regions in contact and no contact. However, energy considerations and application of the principle of Mathematical Induction [18] have shown [19] that, in the foregoing case, the buckled deformed configuration is associated with only one part of the beam in contact with the foundation and the remaining not in contact. This finding was based on a Pasternak tensionless subgrade model, and hence is a fortiori valid for the Winkler model as well.Focusing on establishing the nonlinear stability of PB4, which is an unstable case with profound symmetry, the present work tackles the problem by constructing the total potential energy function of the system and exploring its nature via Catastrophe Theory [20-22]. The three parameter Singularity arising was found to be a special reduced case of the Butterfly, namely the symmetric one [23], with its Bifurcation Set strongly resembling Swallowtail-like sections of the original Singularity [24]. This set, evaluated by means of successive eliminations, as demonstrated by Deng [25], produced critical buckling loads and corresponding deformed configurations. The results obtained were compared with the ones of two more alternative approaches and good agreement was established. It was found that the unstable configuration dealt with herein may appear either prior to or between the in- and-out-of-plane Euler buckling, which may lead to sudden jumps and unexpected bifurcations, a fact of importance for practical design and simulations. This could be avoided by carefully selecting the beam and subgrade parameters, which is not an easy task, since especially the stiffness of the foundation cannot be directly determined [26]. Similar undesirable phenomena have also been reported in the literature, but for bilateral contact only [7, 8, 27, 28].For the completeness and full validation of the present theoretical findings, in their entirety, experiments should be carried out. This task is ongoing by the authors, and hopefully its outcome will be soon available.
2. Problem Description
- We consider a simply supported inextensional Euler-Bernoulli beam of flexural rigidity EI and of uniform cross section, resting on a linear (Winkler type) tensionless foundation, characterized by a stiffness parameter kf, and acted upon by an axial compressive force P. Let W(y) be the beam’s in-plane flexural deflection. The material of the beam is assumed linearly elastic and there are no lateral restrictions. The undeformed pre-buckling configuration is shown in Figure 1, that follows.
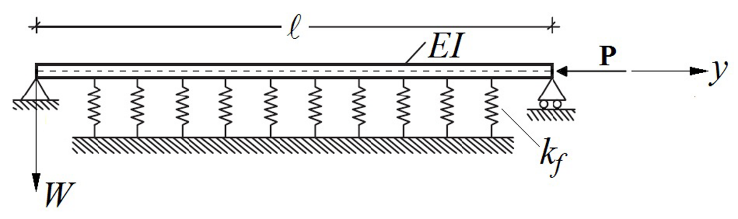 | Figure 1. Axially compressed simply supported beam resting on a Winkler type unilateral elastic foundation |
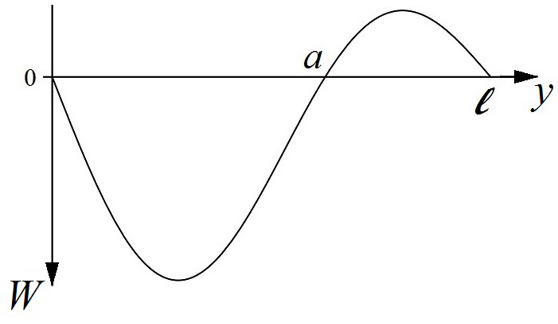 | Figure 2. Postbuckling configuration of the beam dealt with |
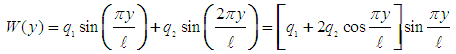 | (1) |
 function satisfies the boundary conditions, and moreover, in order that there is free rotation at the two ends of the beam and one global extremum in the deflection of each region, it is easily found that the ratio of the two state variables q1 and q2, designated as β = q1/q2, must satisfy the inequality
function satisfies the boundary conditions, and moreover, in order that there is free rotation at the two ends of the beam and one global extremum in the deflection of each region, it is easily found that the ratio of the two state variables q1 and q2, designated as β = q1/q2, must satisfy the inequality 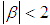 . Additionally, for the function given in Eq. (1) to possess only one more root within the interval
. Additionally, for the function given in Eq. (1) to possess only one more root within the interval 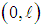 , symbolic computations using the powerful Reduce command embedded in Mathematica [15] yield the following conditions, which represent a logical expression of a clear dissolution – conjunction type,
, symbolic computations using the powerful Reduce command embedded in Mathematica [15] yield the following conditions, which represent a logical expression of a clear dissolution – conjunction type,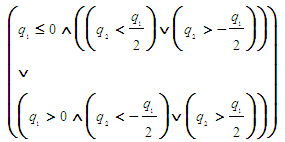 | (2) |
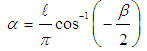 | (3) |
3. Mathematical Formulation
- We then proceed with the evaluation of the system’s total potential energy function VT being in fact the sum of the strain energy due to bending U1, the strain energy due to subgrade reaction U2, and the work of the external force Ω. In doing this, we follow standard procedures of Mechanics and we adopt an approximate nonlinear curvature expression [29, 30] of the form
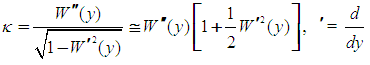 | (4) |
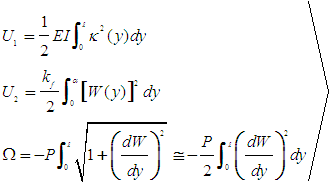 | (5) |
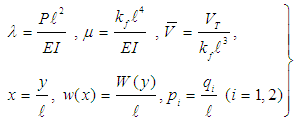 | (6) |
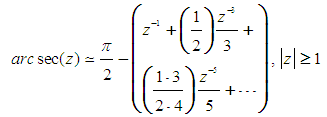 | (7) |
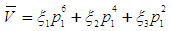 | (8) |
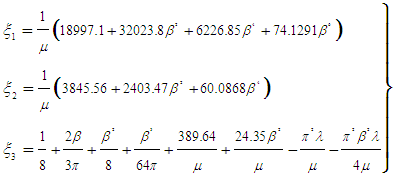 | (9) |
4. Catastrophe Theory Analysis
- In this Section we explore the nature of the truncated total potential energy function of the system, according to the Theory of Catastrophes. Apparently, the function given in Eq. (8), although it can be seen as a reduced – special case of the Butterfly Singularity [21, 22], it still represents a symmetric butterfly function, exhibiting in general a symmetric catastrophe manifold [23]. This feature will be sought by exploring the nature of the foregoing Singularity via an alternative scheme. In doing this, we employ an elimination method, reported by Deng [25], and using simple Algebra, we reach to the Bifurcation Set (Bs) of the Catastrophe at hand. Dropping the subscript of p1 in Eq. (8), the corresponding equilibrium equations at the critical states and the final expression of the Bs are given by:
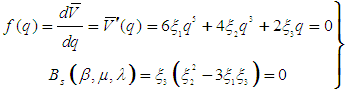 | (10a,b) |
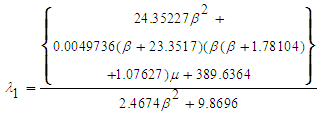 | (11a) |
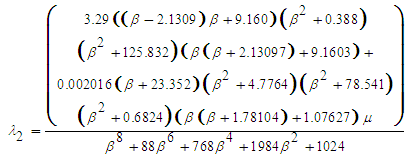 | (11b) |
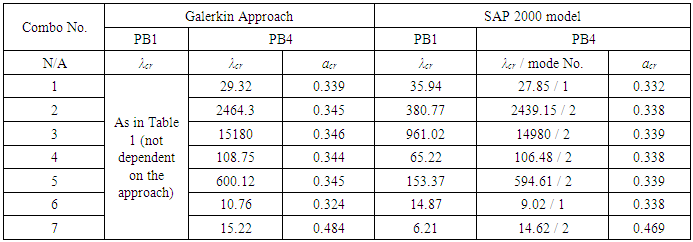
5. Results and Discussion
- Initially the Bifurcation Set defined in Eq. (10b) is presented graphically in terms of three-dimensional contour plots. Due to its strong nonlinearity, a full range reconstruction requires immense computer power, and hence partial range reconstructions are produced for increasing values of λ and μ. These and shown in Figures 3 and 4.
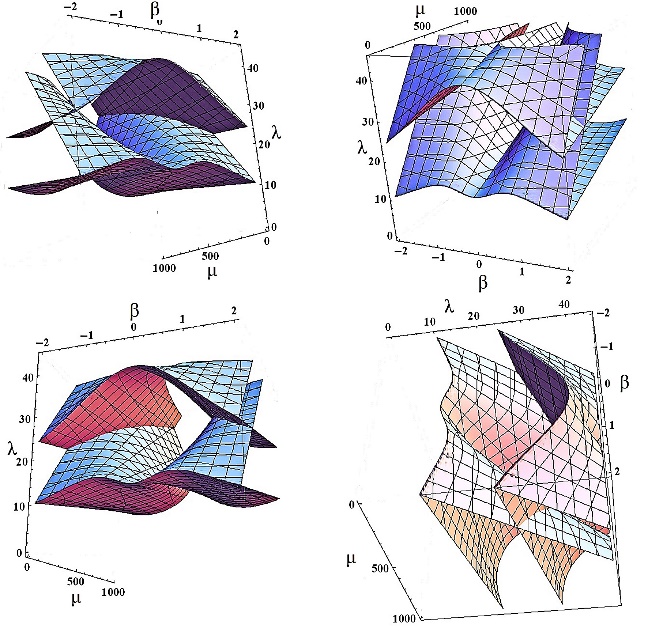 | Figure 3. Partial 3D contour plots of the Bifurcation Set for small values of λ and μ, seen from different viewpoints |
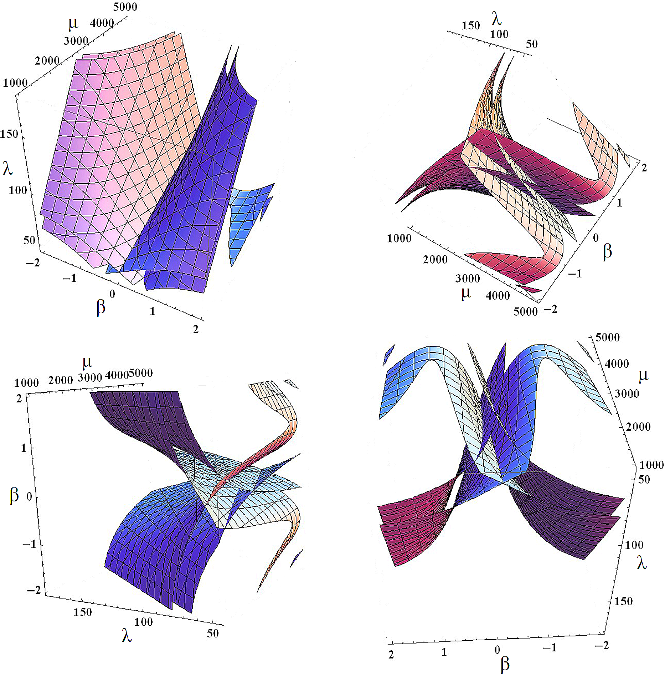 | Figure 4. As in Figure 3, but for large values of λ and μ |
|
|
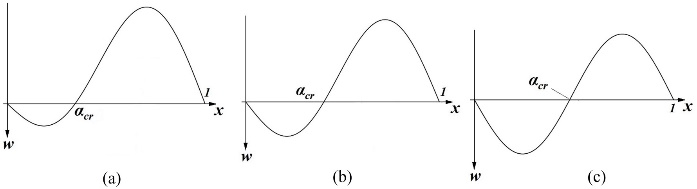 | Figure 5. Qualitative buckled configurations for (a) large, (b) medium, and (c) small values of μ |
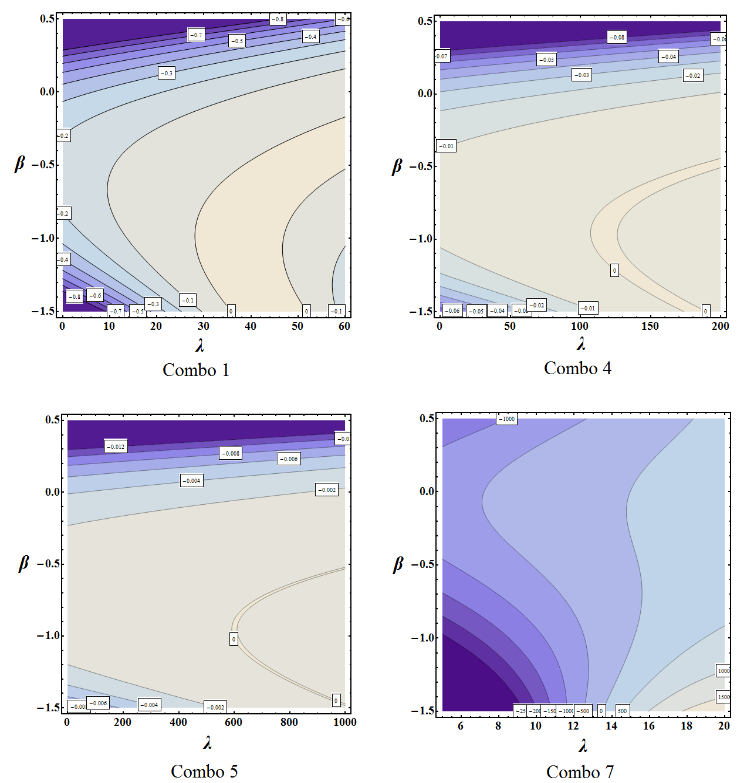 | Figure 6. Sections – contour plots of the Bifurcation Set for four (4) of the combinations of Table 1 |
6. Conclusions
- The most important conclusions drawn from the present study are the following:(a) The consideration of discontinuous (unbonded - unilateral) contact between beam and foundation, being an unstable postbuckling response, leads to a total potential energy function which is a special reduced form of the Butterfly singularity, namely the symmetric one. The resulting three-parameter bifurcation set, an outcome of successive eliminations, resembles Swallowtail-like sections of this particular Catastrophe reported in the literature. Results obtained from the present approach, in terms of critical loads and unbonded beam lengths were found in satisfactory agreement with ones of two alternative approaches.(b) For the cases considered, unstable bifurcations prior to Euler buckling may occur, while also sudden jumps may be possible (a salient feature of the Butterfly Catastrophe), while full contact in a single semi-wave form is not possible. For structural design, these findings are considered of importance, and should be accounted for both in practice and simulations. Similar phenomena have also been reported in the literature for nonlinear bilateral subgrade models.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML