Imane Ed-Dokkali, Larbi El Bakkali
Faculty of Science, Abdelmalek Essaâdi University, Tetouan, Morocco
Correspondence to: Imane Ed-Dokkali, Faculty of Science, Abdelmalek Essaâdi University, Tetouan, Morocco.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
In this work, we study the dynamic phenomenon soliciting blades. The study is results of a simulation tool that shows the distribution of stresses due to the bending mode of the blade during its rotation taking into account both the mechanical forces (centrifugal force, inertial) and secondly , aerodynamic effects. Modeling is made via the finite elements methods, applied to two nodes to estimate the elimination of any kind of damage linked to this mode.
Keywords:
Stress Distribution, Bending Mode, Finite Element Method
Cite this paper: Imane Ed-Dokkali, Larbi El Bakkali, Stress Distribution Dynamic Study Due to the Bending Mode of the Wind Turbine Blade, International Journal of Mechanics and Applications, Vol. 6 No. 4, 2016, pp. 71-76. doi: 10.5923/j.mechanics.20160604.02.
1. Introduction
Wind energy is one of the oldest energy sources used in the world. The wind turbine blades are the most flexible part of this machine, and their modal behavior has a great influence on the overall dynamics and calculating stresses due to the bending mode during the rotation of the blades. Recently more attention has been paid to modal analysis. This reflected by the number of experimental and numerical study conducted on this subject [1]. Indeed, the system bending equation has no exact solution to enable us calculating stress, in addition it is characterized by long complex boundary hampering any digital solution [4], using a finite element modeling with Ansys software, applied to a complex blade shape [2, 5].In this paper, the modeling transverse strain is made applying the finite elements methods based on modal analysis using Matlab code. This method consists in discretization of the blade in small beam elements using the second law of dynamics [3]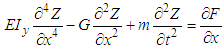 | (1) |
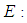 Young's modulus
Young's modulus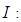 Blade cross section moments of inertia
Blade cross section moments of inertia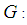 Centrifugal force
Centrifugal force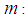 Mass per unit length of bladeThis article includes II paragraph and a paragraph for the description of the results In paragraph I We are interested in the dynamical study of the vibratory movement of the rotating blade. It deals with the forced movement of the blade [8, 9], that is to say the movement of the blade under the effect of aerodynamic loads [12, 13]. The resolution of the forced motion equation is done using the method of modal superposition [12]. This allows us to find the deflection at the free end of the blade and also the stresses acting on the blade that is dealt with in paragraph II.
Mass per unit length of bladeThis article includes II paragraph and a paragraph for the description of the results In paragraph I We are interested in the dynamical study of the vibratory movement of the rotating blade. It deals with the forced movement of the blade [8, 9], that is to say the movement of the blade under the effect of aerodynamic loads [12, 13]. The resolution of the forced motion equation is done using the method of modal superposition [12]. This allows us to find the deflection at the free end of the blade and also the stresses acting on the blade that is dealt with in paragraph II.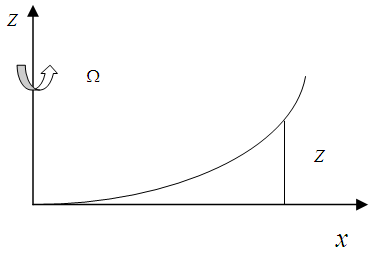 | Figure 1. Deflexion of the blade |
2. Solving the Equation of the Blade Bending Mode by the Finite Element Method
Distribution of Z is represented by the nodal displacement by using the interpolation function [7]: | (2) |
Where  is the interpolation vector that expresses:
is the interpolation vector that expresses: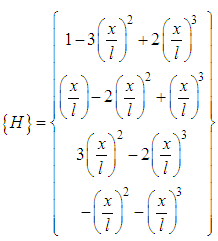 | (3) |
and the vector of degrees of freedom of an element is defined as: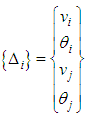 | (4) |
By substituting the formula (2) in (1) and applying the method of weighted residues Galerkin, we obtain the equation for the next element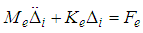 | (5) |
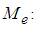 Elementary mass matrix
Elementary mass matrix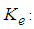 Elementary stiffness matrix
Elementary stiffness matrix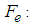 Elementary force vectorThe overall equation of the system is obtained by the assembly of the elementary matrices. The result is shown in figure 2.
Elementary force vectorThe overall equation of the system is obtained by the assembly of the elementary matrices. The result is shown in figure 2.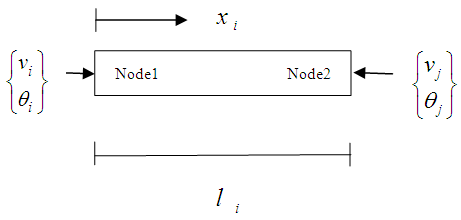 | Figure 2. A finite element showing nodal degrees of freedom |
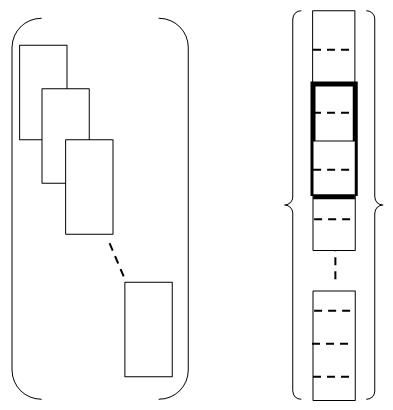 | Figure 3. The assembly process of elementary matrices and elementary vectors forces |
Then there is an equation of motion of the blade in the absence of damping by an equation of the same form as that of an element [10]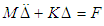 | (6) |
2.1. Boundary Conditions
In This case, we studied a free embedded blade. This condition of embedding one end, involves the cancellation of the potential and kinetic energies at this point, this is equivalent to removing 2 rows and 2 columns of the mass and stiffness matrices in the overall equation of the system.
2.2. Solution Procedure
2.2.1. Study of Free Motion
The motion is free when the blade is not required by external forces, which means that equation (6) becomes equal to zero.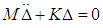 | (7) |
In this case the solution takes the form: 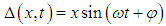 | (8) |
Substituting (9) in the equation (8) we get: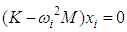 | (9) |
Properties eigenmodes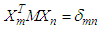 | (10) |
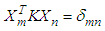 | (11) |
The orthogonality property of the modes will be operated during the study of forced vibrations.
2.2.2. Study of Forced Vibrations
Ÿ A modal superposition methodIn order to decouple the equations, we use the orthogonality property of the eigenmodes. Therefore, it is interesting to rewrite this equation in the base of the natural modes [14]. The displacement Δ is written in matrix form: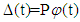 | (12) |
Equation (7) allows having a 2n equation which represents a system with one degree of freedom: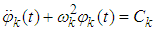 | (13) |
Note that the terms of the first part of the equation for a given mode are independent of the other modes, while the second member (aerodynamic load) depends on all modes since the solution of total strain equation (14) is: 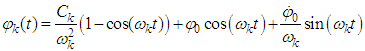 | (14) |
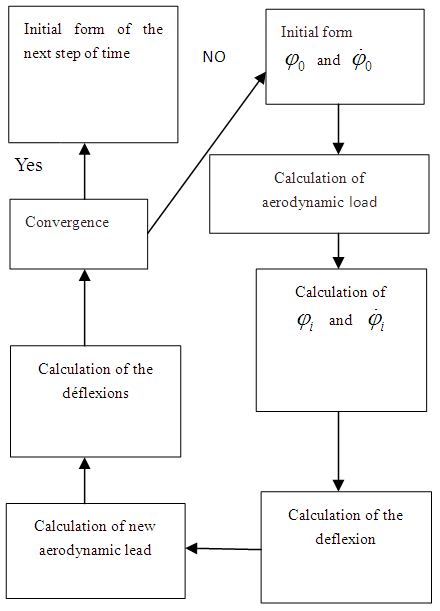 | Figure 4. The flowchart summarizing the method for solving equation (6) |
3. Design Stress
3.1. The Normal Bending Stress
The blade wind turbine is considered as an elastic beam rotating with a constant angular velocity. The blade is treated as a Bernoulli beam clamped-free right. The design stress is due to the bending moment. The blade is considered as a beam Bernoulli clamped-free right to study the stresses acting on the cross section S in a point at a distance Y from the neutral axis. Its equation is: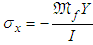 | (15) |
The bending moment Mf is defined as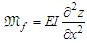 | (16) |
Then from (16) we have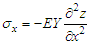 | (17) |
So the constraint of the maximum bending moment is expressed as follows: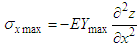 | (18) |
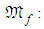 The bending moment to which it is subject.
The bending moment to which it is subject.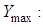 Half the thickness of the blade section
Half the thickness of the blade section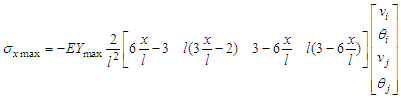 | (19) |
For half element we obtain: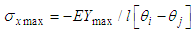 | (20) |
3.2. Normal Stress due to the Centrifugal Force
The expression of the normal stress due to centrifugal force is as follows [6]: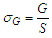 | (21) |
with S is the cross section of the blade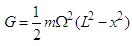 | (22) |
The resulting normal stress: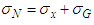 | (23) |
The bending moment is accompanied in most cases with a shearing force. This generates a shear stress. This shear stress generates only little risk of breakage and is therefore generally neglected (Bernoulli model).The tangential stresses is neglected compared to the normal bending stresses for a beam whose length is large compared to the transverse dimensions as the case of the blade.
4. Resultants and Discussion
For numerical simulation of presented below of normal stress, we will take a blade that has the following characteristics hollow section NACA 2414.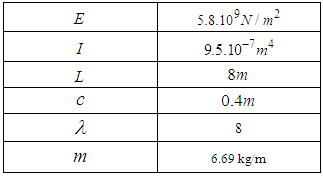
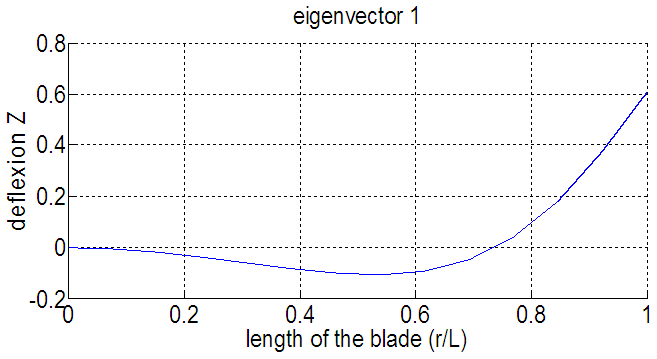 | Figure 5. Eigenmode 1 |
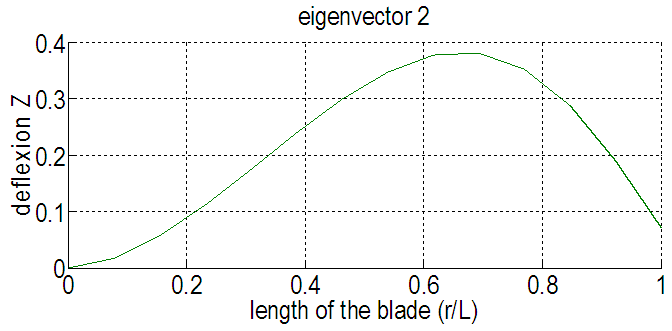 | Figure 6. Eigenmode 2 |
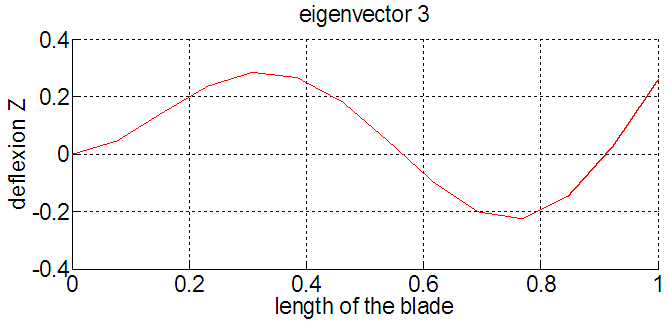 | Figure 7. Eigenmode 3 |
Of all the mechanical vibration problems, the lowest frequency is the most interesting, for this reason, the first three modes are taken into account.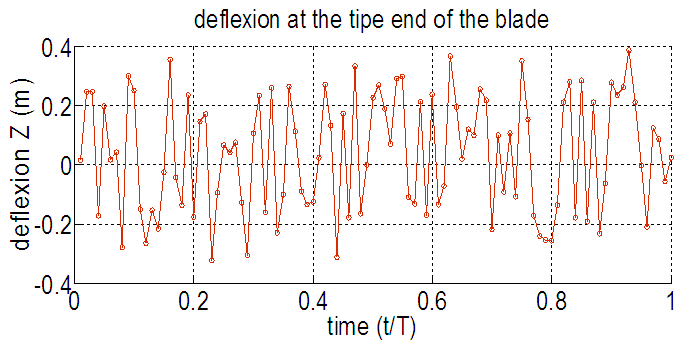 | Figure 8. Deflexion of the tip end of the blade (Ω=12rad/s) |
We can see that the defluxion maximal of the tip end of the blade for Ω = 12rad/s is 0.3875m.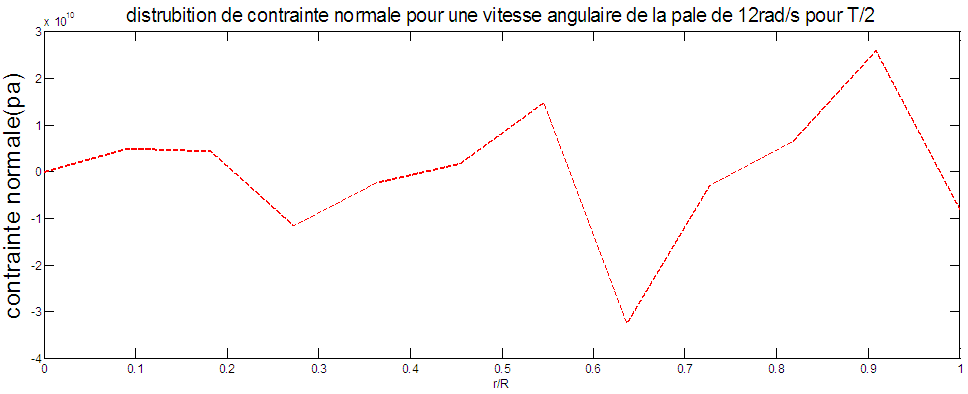 | Figure 9. Normal stress along the blade, Ω=12rad/s, T/2 |
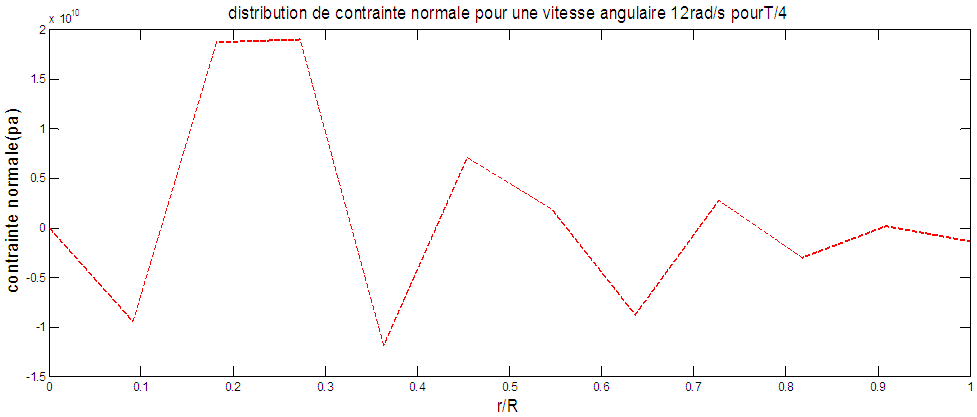 | Figure 10. Normal stress along the blade, Ω=12rad/s, T/4 |
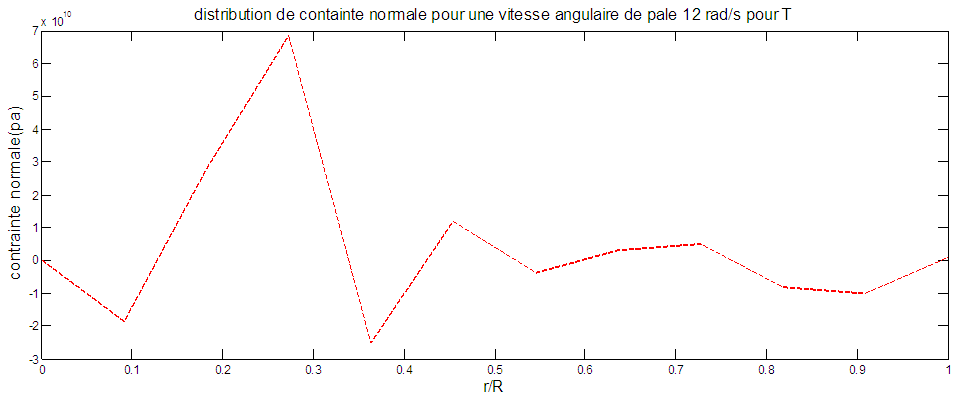 | Figure 11. Normal stress along the blade, Ω=12rad/s, T |
For a blade of a constant angular velocity (12rad/s), the maximum stress is located at the penultimate element of the period (T/2). For period (T/4), maximum stress is located in items 2 and 3. For period (T), the normal stress is in the element 3.
5. Conclusions and Perspectives
The aim of this work is to develop a mathematical model of analysis to solving the equation of the bending of the blade and that Allows to study the normal stress of wind turbine blade subjected to aerodynamic loads. This profound study, allows us to calculate slowness of the blade and to estimate its lifetime.
References
| [1] | Chellil A., “Indentification et modélisation par élément fini des charge dynamique du rotor principale d’hélicoptère’’. Université de boumerdes, Faculté des sciences de l’Ingénieur, 2008. |
| [2] | Mahri Z. L., “Etude dynamique et optimisation des pales d’un aérogénérateur’’ Thèse de doctorat, University Mentouri Constantine, Faculté des sciences de l’Ingénieur, 2007. |
| [3] | CHELIREM T., “Etude dynamique d’une pale d’éolienne effilée’’., Magester. Mentouri Constantine, Faculté des sciences exact, jun 2010. |
| [4] | Ed-dokkali I., El bakkali L, “Modélisation de flexibilité de la pale en utilisant la Méthodes des éléments finis’’., 2 éme congrés de mécanique 22-25 aprill 2015-Casablanca, (1). |
| [5] | A. R. S. Bramwell. (1979), “Helicopter dynamics, Edt Edward Arnold’’, 1979. |
| [6] | Samper. S., “Comportement dynamique de poutre composite préchargées: Modélisation par éléments finis’’, Université Paule Sabatier Toulouse III. 1994. |
| [7] | PAULTRE, P. (2005), “Dynamique des structures Lavoisier, first edition’’, 2005. |
| [8] | Wang, Z. J., “Aerodynamic efficiency of flapping flight: analysis of a two-stroke model’’, Journal of Experimental Biology, 2008, 211(2), 234-238. |
| [9] | Chopra, A. K., “Dynamics of structures”. New Jersey: Prentice Hall.1995, (3). |
| [10] | Gherbi, M. T., “Modélisation par éléments finis d’une pâle d’hélicoptère sous chargement aérodynamique’’, Université Boumerdès, Faculté des sciences de l’Ingénieur, 2010. |
| [11] | Delaplace, A., Gatuingt, F., & Ragueneau, F., “Aide-mémoire de mécanique des structures-Résistance des matériaux: Résistance des matériaux. Dunod’’, 2008. |
| [12] | Ed-dokkali Imane El bakkali Larbi, “Modeling the bending of the blade windturbine Using Finite Element Analysis’’, IOSR Journal of applied physics, Jul. - Aug. 2016, (8), 78-86. |
| [13] | M. philippe, A. Babarit, P. Ferrant, “étude des modes propres et de réponse forcée d’une éolienne offstorre flottante soumise à une houle direction croisée par rapport à celle du vent’’ 12émes journées de l’hydrodynamique Nantes, 17-19 nove mbre 2010. |
| [14] | M. Nadjah, M. Khechana, et C. Mahfoudi « Etude de l’hélice d’une éolienne de 5 kW », Revue des Energies Renouvelables CISM08, 2008. |



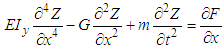
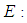 Young's modulus
Young's modulus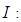 Blade cross section moments of inertia
Blade cross section moments of inertia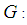 Centrifugal force
Centrifugal force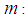 Mass per unit length of bladeThis article includes II paragraph and a paragraph for the description of the results In paragraph I We are interested in the dynamical study of the vibratory movement of the rotating blade. It deals with the forced movement of the blade [8, 9], that is to say the movement of the blade under the effect of aerodynamic loads [12, 13]. The resolution of the forced motion equation is done using the method of modal superposition [12]. This allows us to find the deflection at the free end of the blade and also the stresses acting on the blade that is dealt with in paragraph II.
Mass per unit length of bladeThis article includes II paragraph and a paragraph for the description of the results In paragraph I We are interested in the dynamical study of the vibratory movement of the rotating blade. It deals with the forced movement of the blade [8, 9], that is to say the movement of the blade under the effect of aerodynamic loads [12, 13]. The resolution of the forced motion equation is done using the method of modal superposition [12]. This allows us to find the deflection at the free end of the blade and also the stresses acting on the blade that is dealt with in paragraph II.
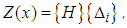
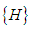 is the interpolation vector that expresses:
is the interpolation vector that expresses: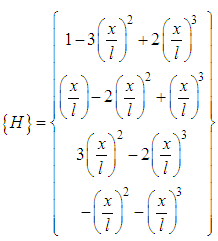
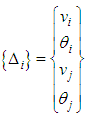
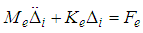
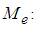 Elementary mass matrix
Elementary mass matrix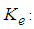 Elementary stiffness matrix
Elementary stiffness matrix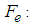 Elementary force vectorThe overall equation of the system is obtained by the assembly of the elementary matrices. The result is shown in figure 2.
Elementary force vectorThe overall equation of the system is obtained by the assembly of the elementary matrices. The result is shown in figure 2.

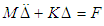
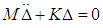
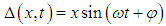
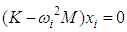
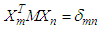
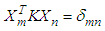
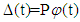
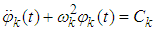
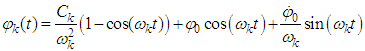

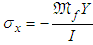
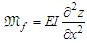
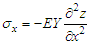
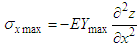
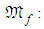 The bending moment to which it is subject.
The bending moment to which it is subject.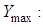 Half the thickness of the blade section
Half the thickness of the blade section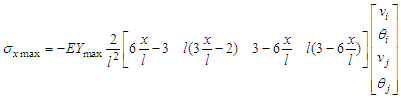
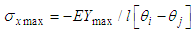
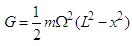
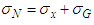








 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML