Cláudio José Martins, Ludmila Moura Moreira Mendes
Department of Civil Engineering, CEFET-MG, Belo Horizonte, Brazil
Correspondence to: Cláudio José Martins, Department of Civil Engineering, CEFET-MG, Belo Horizonte, Brazil.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
This paper aims to report a simple and fast procedure to determine translational, rotational and torsional stiffness of wind tower foundations. The manufacturers of these structures establishing stiffness as a very important parameter for the foundations design. Usually the stiffness is estimated in the design stage considering empirical formulations, but several cases are reported pointing out that empirical procedures have conduced to significant differences from real values. At this paper the real stiffness of two wind tower foundations, one operating and another stopped, were obtained by constructing numerical models and fitting its modal parameters until reach real ones. Real modal parameters were obtained by conducting operational modal analysis over those structures. Results indicates that vibrations due tower under operation did not affect extraction of experimental values and also it was showed that modal analysis represents the structural behaviour of wind towers with good reliability, becoming an efficient and simple procedure to determine real stiffness of foundations.
Keywords:
Dynamic of foundations, Operational modal analysis, Soil-Structure interaction
Cite this paper: Cláudio José Martins, Ludmila Moura Moreira Mendes, Determination of Stiffness for Wind Tower Foundation by Operational Modal Analysis, International Journal of Mechanics and Applications, Vol. 6 No. 3, 2016, pp. 43-48. doi: 10.5923/j.mechanics.20160603.02.
1. Introduction
The wind power has increasing participation in the world energetic matrix. Alvarez et al. [1] explains that it has occurred due two main reasons: the reduction of costs in 90% since the beginning of the 1980-decade and governmental subsidies. In Brazil, the participation of this energetic source has grown expressively in recent years. Melo [2] pointed out the implantation of the Program for Incentive to Alternative Energy Sources and the international economic crisis of 2008 as the causes of improvement of wind power in Brazil. The international crisis caused decrease of the investments in renewable sources in Europe and United States, turning Brazil very attractive country for wind power companies. Currently the wind energy is the second more competitive source of electric energy in Brazil. According to International Renewable Energy Agency (IRENA) [3] the sector was increased 42% in Latin America and Caribbean in 2015, and countries Brazil, Mexico, Panama and Uruguay accounted for 88% of this increase.Wind towers are subjected to dynamic actions of wind, consequently the dynamic behavior must be controlled in order to avoid resonance between external loads and tower vibration modes, once the resonance phenomenon could cause high tensions and speed up fatigue process. According to Liingaard et al. [4] wind turbines have become more sensitive to the dynamic action of low frequency. This occurs due to changes aiming costs reduction and increase productivity.This work studied dynamic aspects for pile foundation of two wind towers considering modal analyses, taking into account properties related to your dynamic behavior: natural frequencies, rate of damping and vibration modes. The achievement of dynamic characteristics for these structures was accomplished by operational modal tests. In these tests was observed only the answer of the system, what means that loads are due its operation and wind. Thus, it was not necessary to interrupt the structure's normal work and was required only equipments for vibration measurement to conduce the test.The modal analysis usually associates the finite element method (FEM) and the experimental determination of structural modal properties. Commonly a FEM numerical model is developed and modal parameters fitted to the experimental data. This process induces modifications on numerical model until the simulation and experimental data become sufficiently close. After this process, FEM model can be used to predict real stiffness of foundations.Some researches about modal analysis of wind towers have been conducted with different goals. Shirzadeh et al. [5] performed operational modal analysis for offshore wind turbine in order to identify damping for first mode during the normal operation and at rotor-stop tests. It was observed that damping rates obtained in the numerical simulations for both tests were similar, indicating good reliability.Damgaard et al. [6] performed more than 1500 rotor-stop tests for offshore wind towers considering operational modal analysis. The features that affect the damping were evaluated on real towers and numerical models. It was observed that structural dampings are affected by the transport of sediments in the seabed, and it was found that simulation of blade rotating affect damping. According to Ciang et al. [7] operational modal analysis is also relevant for health monitoring of wind towers, because modal analysis is non-destructive and does not interfere with structure operation. An application of modal analysis for health monitoring was developed by Currie et al [8]. They elaborated a wireless structural integrity monitoring (SIM) to monitor the vertical displacement of the embedded ring in onshore concrete foundations. They also associated the dynamic behaviour of wind turbines to the structural cracks were commonly observed in the concrete pedestals.According to AlHamaydeh and Hussain [9] the design of foundations is very important for wind turbines construction, since foundations are frequently the only component designed to a specific situation, it consider soil properties and the required stiffness for the system. At AlHamaydeh and Hussain work, several types of foundation for onshore wind towers were simulated, and it was observed that the consideration of foundation concept reduce the stiffness of the tower-foundation set. Fact reiterated by the work of Bisoi and Haldar [10], in which several parameters were studied in offshore generators with monopile foundations at clay. It was noticed that the consideration of the foundation in the model, contributes to increase the flexibility of the structure, so, it reduces the eigenfrequencies. At other work of Bisoi and Haldar [11], it was verified that fundamental frequency of the wind tower increases if the monopile is embedded at rigid soil. Jung et al. [12] compared different foundation modelling approaches, using p-y curves and FEM, they observed that ignoring the flexibility of the foundation produced significant error in natural frequency measurement. They found first and second natural frequencies approximately 15% higher than the models considering the foundation flexibility. In the paper of Arany et al. [13] they also were observed a typical reduction by 4–15% for flexibility of offshore wind turbines foundation.The work of Shi et al. [14] also shows the influence of the foundation on stiffness and natural frequencies of offshore wind towers. Three types of foundations were simulated, for the same wind tower and same conditions: monopole, multipile and jacket. The result shows that jacket foundation is less stiff than others and multipiles is stiffer and have higher frequencies than others.Some previous works shows the influence of the foundation on modal tower parameters. Despite this importance, the design of a tower foundation usually is based on stiffness and soil parameters frequently obtained by empirical formulas. Considering this, it is possible that the adopted stiffness at design stage presents significant difference of real stiffness. In the present work, it's presented a simple and fast way to obtain real stiffness (translational, rotational and torsional directions) for wind towers foundation. The procedure is based on the operational modal analysis. It's necessary only portable accelerometers and data acquisition system and it's not necessary to interrupt operation of towers. The towers were found at different operation situation: one was active while another inactive; Stiffness for both situations was compared, and it was observed that they presented similar values, in despite of the wind tower was under operation or not.
2. Structure and Soil Description
The operational modal tests were performed in two Gamesa G97 2MW wind turbines presented at figure 1. The towers are composed of three steel tubular parts. Height after assembly is 78 m and weighs 1314.09 kN. The wind turbine has three blades that weigh 78.45 kN each one and presents length 47.50 m. The hub weighs 245.16 kN and has 2.00 m of diameter, while nacelle weighs 745.30 kN. | Figure 1. Wind tower model Gamesa G97 |
This work is focused at foundation of two wind towers; both have the same design shown at figure 2. The foundation has 14 m diameter and 18 borehole piles with 10.80 m deep. The piles have a diameter of 0.70 m and are arranged radially at a distance of 6.25m from center. The concrete of the piles has compressive strength 20 MPa. The tower connects to the foundation by 128 prestressed bolts.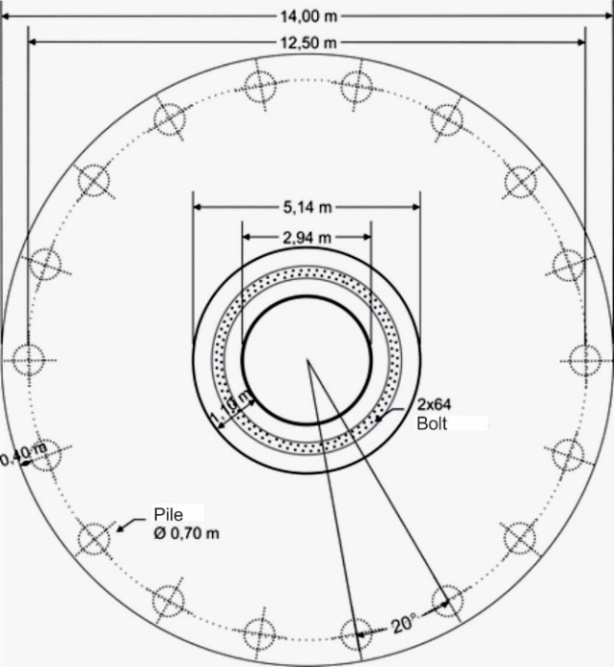 | Figure 2. Foundation plan |
The pile cap can be divided into three geometric shapes: a circle, a truncated cone and a ring. The circle has 1.00 m thick and 14.00 m for diameter. The truncated cone has 1.75 m height, base diameter 14.00m and top diameter 5.14 meters. The circle and the truncated cone present concrete with compressive strength 30 MPa. Ring has 5.14 m for external diameter, 2.94m for internal diameter, and it was casted by concrete with compressive strength of 40 MPa. The specific weight of the concrete is 23.56 kN/m³. The report of the Standard Penetration Test (SPT) considered 10 investigation points. It indicates variation on the water table between 0.6 to 2.7 m in deep. The upper soil layer is thin and is characterized by compounds of sandy clay or silt, resistance from rigid to soft. To deep soil layers, there are thick layers of fine sand; their resistance varies from moderately compact, compact until very compact.
3. Ambient Excitation Test
Two ambient excitation tests were performed. The first was conducted on inactive tower (tower A) while second on active one (tower B). Each test employed two devices with triaxial accelerometers of Syscom Instruments. The equipment has 24-bit resolution, measuring range between -2 g to +2 g. The accelerometers were placed at two points over pile cap top, considering X axis oriented to the tower center, as shown in figure 3. The accelerometers were synchronized, data was recorded for 4 h and it was adopted sampling rate of 100 Hz.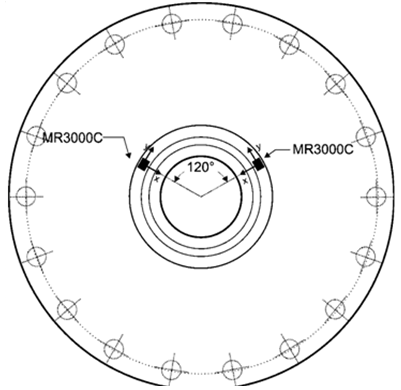 | Figure 3. Experimental arrangement |
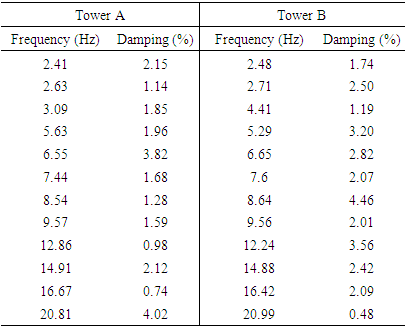
The ambient excitation test responses provided time series of the accelerations. The eigenfrequencies and damping rate were obtained by Enhanced Frequency Domain Decomposition (EFDD) using Artemis Modal 3.0 software. The eigenfrequencies obtained in the ambient excitation test and their damping ratios are appointed at table 1.Table 1. Frequencies and rate damping from experimental data
 |
| |
|
4. Numerical Models
Primarily was developed an model based on design information only. The software used was SAP2000, program based on finite element method (Fig. 4). The tower was constituted by 648 thin shells elements. The foundation was modelled by 828 shell elements with variable thickness and 18 links were adopted to represent piles. The model is shown at figure 4.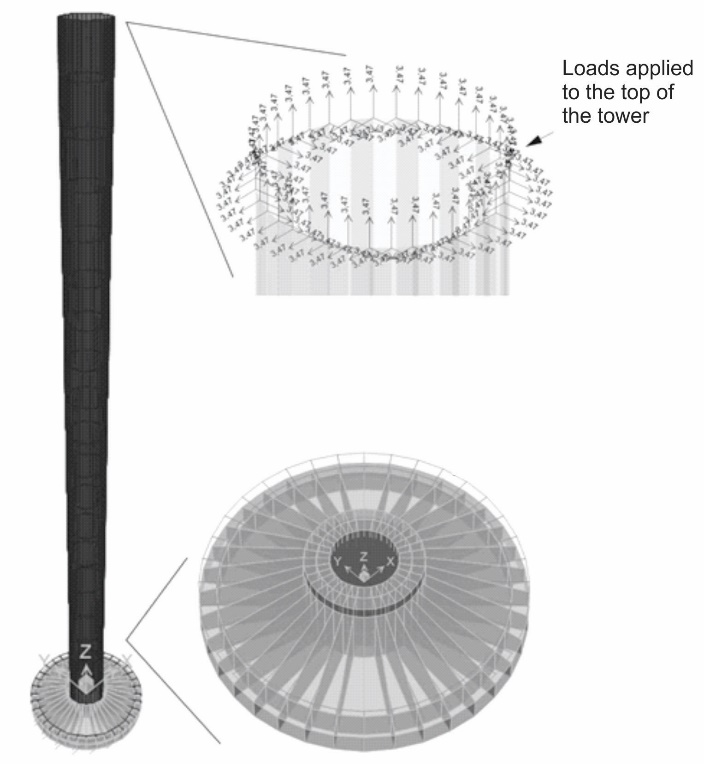 | Figure 4. Numerical model |
The standard penetration test data was used to estimate soil springs coefficients, considering empirical tables. The variation of soil spring coefficients along depth is shown on table 2.Table 2. Spring coefficients along soil depth
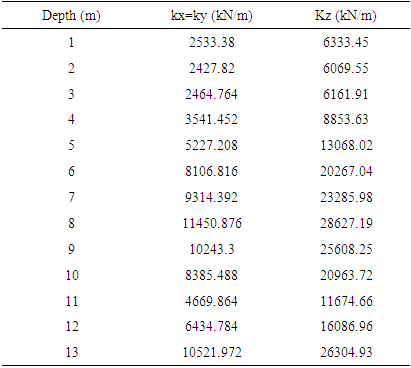 |
| |
|
The stiffness of piles was obtained by numerical simulation of a single pile. The soil spring coefficients from table 2 were inserted each meter deep. In this model was applied unitary forces and moments at top, with goal to define translational and rotational stiffness. The displacements in each direction were extracted, and by this way stiffness for individual piles were defined. These values were employed in the wind tower model, replacing by links with the obtained stiffness coefficients.
5. Results
The initial model was adapted to experimental modal parameters (table 1) of tower A and B. In this process pile springs were changed until experimental and numerical natural frequencies had presented good approximation. The error reductions related experimental natural frequency values are presented in figure 5. The results for updated models are shown in table 3. Table 4 presents stiffness obtained for piles before and after updating while stiffness for foundations before and after adaptation are presented on table 5. The stiffness variation of piles and foundations related to initial model are shown on tables 6 and 7, respectively.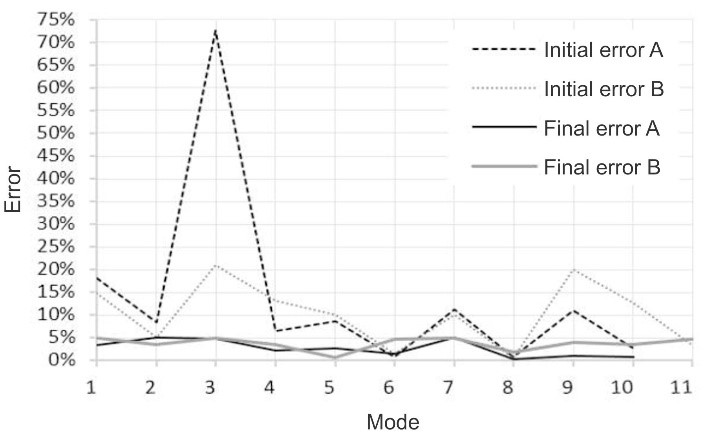 | Figure 5. Eigenfrequencies error related to experimental data |
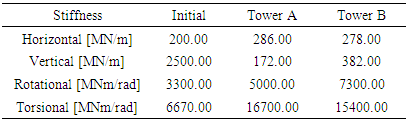
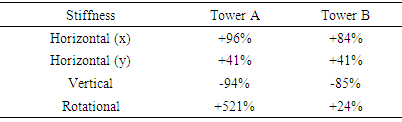
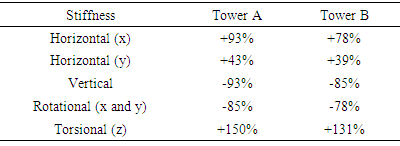
Although the wind towers A and B are located at different places, they presented similarity in the stiffness foundation obtained by this work. Table 7 shows that the towers have similar variations in relation to the initial model. It's showed at table 3 that natural frequencies of towers A and B are similar. The exception is third mode frequency of tower B, 43% bigger than the third mode frequency of tower A. This information is confirmed in table 5, that shows the vertical stiffness of tower B is 122% bigger than tower A. Table 5 also shows that the rotational stiffness of tower B is 46% bigger than tower A, however shows similar values for horizontal and torsional stiffness.Table 5 indicates that horizontal and translational stiffness are very similar for towers. Flexural stiffness presents about 30% difference while vertical direction presents a variation about 120%, last value due significant vertical variation of individual piles showed at table 4.Table 3. Updated Eigenfrequencies (Hz) for tower A and B
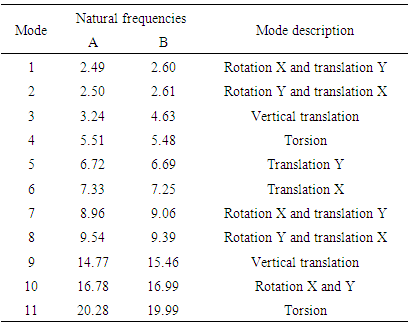 |
| |
|
Table 4. Piles stiffness: initial, towers A and B models
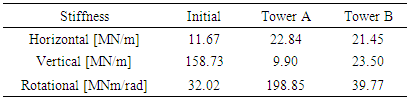 |
| |
|
Table 5. Foundation stiffness: initial, towers A and B models
 |
| |
|
Table 6. Piles stiffness variation: updated A and B
 |
| |
|
Table 7. Foundation stiffness variation: models A and B
 |
| |
|
6. Conclusions
This work presented a simple and practical procedure to determine real stiffness of wind tower foundations. The accelerations were evaluated in two points of the foundation and then the data collected was processed. Numerical simulations were done, and by this way, translational, rotational and torsional stiffness based on experimental data were obtained.The numerical models for towers A and B represent the real structures efficiently, because after updating, variation between the values measured on the experiment and values of models are under than 5% (Fig. 5). The dynamic behaviours of towers are similar since various modes presented close values and patterns. The results indicate that operational modes produced by vibrations of tower operation did not affect the procedure, since both structures had presented similar foundation stiffness and frequency spectra.Finally, it is observed that a significant difference between empirical and experimental stiffness values was found. Therefore, it is possible to observe that the empirical adoption for stiffness of wind towers must be verified by experimental values, avoiding design failures in dynamic response of these structures. It was showed that modal analyses present a simple, fast and accurate procedure to determine the real foundation stiffness.
ACKNOWLEDGEMENTS
The authors acknowledge the financial support by FAPEMIG and CEFET/MG and operational support by Terratek, PavSolo and Eletrosul - Centais Elétricas S.A.
References
| [1] | Alvarez, J. M. G.; Schweickardt, G.; Targarona, J. C. G. 2012. “An overview of wind energy, taking into consideration several important issues including an analysis of regulatory requirements for the connection of Wind generation into the power system”. Dyna 172:108-117. |
| [2] | Melo, E. 2013. “Wind energy source: Insertion aspects, technology and competitiveness”. Estud. av. 77:125-142. |
| [3] | IRENA. “Renewables in Latin America and the Caribbean”. 2016. 〈http://www.irena.org/DocumentDownloads /Publications/LAC_stats_highlights_2016.pdf〉. |
| [4] | Liingaard, M.; Andersen, L.; Ibsen, L. B. 2007. “Impedance of flexible suction caissons”. Earthquake Engineering and Structural Dynamics 36:2249-2271. |
| [5] | Shirzadeh, R. et al. 2013.”Experimental and computational damping estimation of an offshore wind turbine on a monopile foundation’. Journal of Wind Engineering and Industrial Aerodynamics 120:96-106. |
| [6] | Damgaard, M. et al. 2013. “Cross-wind modal properties of offshore wind turbines identified by full scale testing”. Journal of Wind Engineering and Industrial Aerodynamics 116:94-108. |
| [7] | Ciang, C.; Lee, J.; Bang, H. 2008. “Structural health monitoring for a wind turbine system: a review of damage detection methods”. Measurementscience and Technology 19:122001. |
| [8] | Currie M.; Saafi M.; Tachtatzis C.; Quail F. 2015. “Structural integrity monitoring of onshore wind turbine concrete foundations”. Renewable Energy 83: 1131e1138. |
| [9] | Alhamaydeh, M.; Hussain, S. 2010. “Optimized frequency-based foundation desing for Wind turbine towers utilizing soil-structure interaction”. Journal of the Franklin Institute 348:1470-1487. |
| [10] | Bisoi, S.; Haldar, S. 2014. “Dynamic analysis of offshore wind turbine in clay considering soil-monopile-tower interaction”. Soil Dynamics and Earthquake Engineering 63:19-35. |
| [11] | Bisoi, S.; Haldar, S. 2015. “Design of monopile supported offshore wind turbine in clay considering dynamic soil–structure-interaction”. Soil Dynamics and Earthquake Engineering 73:103-117. |
| [12] | Jung, S.; Kim S.; Patil A.; Hung L. C. 2015. “Effect of monopile foundation modeling on the structural response of a 5-MW offshore wind turbine tower”. Ocean Engineering 109:479-488. |
| [13] | Arany L.; Bhattacharya, S.; Macdonald, J.H.G.; Hogan S. J. 2016. “Closed form solution of Eigen frequency of monopile supported offshore wind turbines in deeper waters incorporating stiffness of substructure and SSI”. Soil Dynamics and Earthquake Engineering 83:18-32. |
| [14] | Shi, W. et al. 2014. “Feasibility study of offshore wind turbine substructures for southwest offshore wind farm project in Korea”. Renewable Energy 74:406-413. |








 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML





