-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Mechanics and Applications
p-ISSN: 2165-9281 e-ISSN: 2165-9303
2016; 6(2): 25-30
doi:10.5923/j.mechanics.20160602.02

Energetic Study of Some States of Debonding in the Composite Structures
Yahya Berrehili, Abdelmoutalib Berrehili, Mohammed Rahmoune
Equipe de Modélisation et Simulation Numérique, Université Mohamed 1er, Ecole Nationale des Sciences Appliquées, Oujda, Maroc
Correspondence to: Yahya Berrehili, Equipe de Modélisation et Simulation Numérique, Université Mohamed 1er, Ecole Nationale des Sciences Appliquées, Oujda, Maroc.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

In this paper, a qualitative study is first given to show the influence of the laws of contact, imposed on the constituents interfaces(inclusions-matrix), as well as of type of composites and type of defects or decohesions, on the effective behavior of the “debonded” composite materials. A quantitative analysis is then discussed: we present an energy analysis of some model states of decohesion than may have a composite structure. This energetic study, based on the theory of Francfort and Marigo, consists primarily to reject, for a loading level and a given surface energy (in order of magnitude of 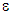 with
with 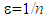 and where n denotes the number of fibers contained in the structure), the decohesions leading to highest energies of medium. The obtained results of this study are interesting, interesting insofar as they can be used in high tech industry to ensure that of this or that debonding can not appear in such composite pieces, subjected to loading of their use services.
and where n denotes the number of fibers contained in the structure), the decohesions leading to highest energies of medium. The obtained results of this study are interesting, interesting insofar as they can be used in high tech industry to ensure that of this or that debonding can not appear in such composite pieces, subjected to loading of their use services.
Keywords: Composite, Homogenization, Matched asymptotic expansion, Surface energy, Energy of medium
Cite this paper: Yahya Berrehili, Abdelmoutalib Berrehili, Mohammed Rahmoune, Energetic Study of Some States of Debonding in the Composite Structures, International Journal of Mechanics and Applications, Vol. 6 No. 2, 2016, pp. 25-30. doi: 10.5923/j.mechanics.20160602.02.
Article Outline
1. Introduction
- For several years, many damage models have been proposed to describe the debonding in the composite structures (see [18] [21] [25] [26] [28]). Among these models, there exist an approach based on fracture mechanics, which deals the decohesion of the constituents interfaces as a cracking problem. It postulates that the debonding, supposedly pre-existing, will spread when the elastic energy restitution rate exactly offsets the surface energy needed for the creation of new debonding areas. These areas are supposed unit, i.e. of the same order of magnitude of
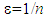 where
where 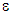 being the parameter characteristic of the microstructure defined by the number of fibers n contained in the composite structure. It comes to the Griffith's approach [17]. Unfortunately it can not treat the initiation problem of debonding or cracking in general. In starting from its philosophy, but not from its criterion, Francfort and Marigo [9] [14] [15] have developed a new prediction formulation of the initiation and propagation of cracks in sound structures or pre-cracked. By assigning a surface energy thereto, the formulation consist, roughly speaking, to searching, for a given loading level, the cracking leading to the smallest energy of the medium. The energy of the medium being defined as the sum of its elastic energy and its surface energy
being the parameter characteristic of the microstructure defined by the number of fibers n contained in the composite structure. It comes to the Griffith's approach [17]. Unfortunately it can not treat the initiation problem of debonding or cracking in general. In starting from its philosophy, but not from its criterion, Francfort and Marigo [9] [14] [15] have developed a new prediction formulation of the initiation and propagation of cracks in sound structures or pre-cracked. By assigning a surface energy thereto, the formulation consist, roughly speaking, to searching, for a given loading level, the cracking leading to the smallest energy of the medium. The energy of the medium being defined as the sum of its elastic energy and its surface energy 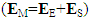 [10] [11] [22] [23]. For the problem of debonding in composite materials, it is necessary to introduce the characteristic functions
[10] [11] [22] [23]. For the problem of debonding in composite materials, it is necessary to introduce the characteristic functions 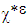 characterizing decohesion states of a composite structure [7], which is worth 0 on the bonded part of the interface, noted
characterizing decohesion states of a composite structure [7], which is worth 0 on the bonded part of the interface, noted 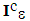 and which is worth 1 on the debonded complementary part, noted
and which is worth 1 on the debonded complementary part, noted 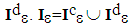 being the set of all interfaces, bonded and debonded. We also note by
being the set of all interfaces, bonded and debonded. We also note by 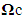 and
and 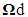 the composite structures whose components are bonded respectively debonded.
the composite structures whose components are bonded respectively debonded. 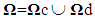 is the domain occupied by the composite structure considered. We also talk of states of cracking or debonding to designate any state of decohesion of the composite structure. The decohesion problem of Francfort and Marigo consist then at finding the fields couple
is the domain occupied by the composite structure considered. We also talk of states of cracking or debonding to designate any state of decohesion of the composite structure. The decohesion problem of Francfort and Marigo consist then at finding the fields couple 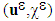 , displacement field and state function, minimizing energy of the medium,
, displacement field and state function, minimizing energy of the medium,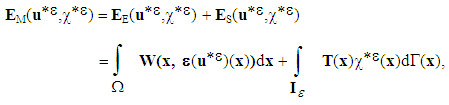 | (1) |
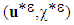 (admissible displacement field and admissible characteristic function).
(admissible displacement field and admissible characteristic function). 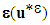 and
and 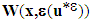 designate respectively, the strain tensor of the displacement field
designate respectively, the strain tensor of the displacement field 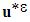 and the elastic deformation potential associated with this field, at point x. T(x) denotes the tenacity of interfaces [7] [27]. Thereafter, it will be assumed that there is continuity of the normal displacement field of
and the elastic deformation potential associated with this field, at point x. T(x) denotes the tenacity of interfaces [7] [27]. Thereafter, it will be assumed that there is continuity of the normal displacement field of 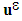 on the debonded interfaces. The tenacity is therefore assumed to be constant on all interfaces, bonded and debonded
on the debonded interfaces. The tenacity is therefore assumed to be constant on all interfaces, bonded and debonded 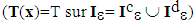 .
.2. Elastic Potential and Surface Energy of a Composite with Debonded Constituents
- We have shown in [2] and [3] that the potential or the elastic energy (1) takes different forms depending on whether the constituents of the medium are bonded or debonded. In the bonded case the energy of the medium is equal to its elastic energy, in other words, its surface energy is zero (see for example [20]). This is because the states functions
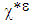 are zero on all interfaces, since they are all bonded
are zero on all interfaces, since they are all bonded 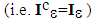 . We have then,
. We have then,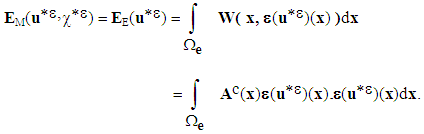 | (2) |
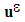 , unique solution of the energy minimization problem
, unique solution of the energy minimization problem 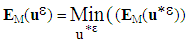 among all kinematically "admissible" fields, is the solution field of the real problem (see [2]). Therefore it is continuous over the entire composite structure
among all kinematically "admissible" fields, is the solution field of the real problem (see [2]). Therefore it is continuous over the entire composite structure 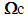 . And since the basic cell associated, denoted V, is a connected part of IR2, it is approached in first order, by:
. And since the basic cell associated, denoted V, is a connected part of IR2, it is approached in first order, by: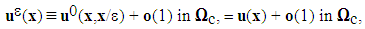 | (3) |
 and u the classical displacement field encountered in theory of periodic homogenization (see eg [3]). In the debonded case
and u the classical displacement field encountered in theory of periodic homogenization (see eg [3]). In the debonded case 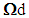 (but with contact and perfect relative sliding between constituents), the energy of medium (1) takes an other form. It was shown in [2] that the field in question
(but with contact and perfect relative sliding between constituents), the energy of medium (1) takes an other form. It was shown in [2] that the field in question 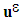 is approached by
is approached by 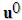 , given by:
, given by: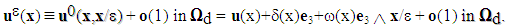 | (4) |
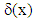 and
and 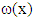 are new scalar fields interpreted as the internal slip and internal rotation of the debonded composite structure. In fact they represent real sliding and rotations of fibers in the microstructure, indexed by the macroscopic variable x. They are extended in the matrix by the value 0 and therefore are discontinuous in general on the interfaces. The energy of medium to minimize is then written, in the case of a fibered composite,
are new scalar fields interpreted as the internal slip and internal rotation of the debonded composite structure. In fact they represent real sliding and rotations of fibers in the microstructure, indexed by the macroscopic variable x. They are extended in the matrix by the value 0 and therefore are discontinuous in general on the interfaces. The energy of medium to minimize is then written, in the case of a fibered composite,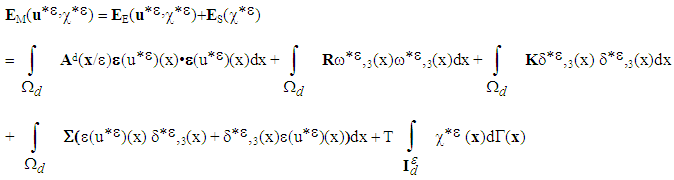 | (5) |
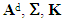 and
and 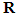 are quantities that are defined and interpreted in [2]. They are given by solving 12 elementary problems, on the basis cell V\I associated with the debonded part, instead of 6 problems in the bonded case. T is the tenacity of the debonded interfaces assumed constant as was stated in the introduction.Remark 1.In theory, one speaks of rotation of a solid (deformable or no) but not of a material point. Therefore, there is no loading working in rotation at each point of the structure. We conclude then that the internal rotation is zero, i.e.
are quantities that are defined and interpreted in [2]. They are given by solving 12 elementary problems, on the basis cell V\I associated with the debonded part, instead of 6 problems in the bonded case. T is the tenacity of the debonded interfaces assumed constant as was stated in the introduction.Remark 1.In theory, one speaks of rotation of a solid (deformable or no) but not of a material point. Therefore, there is no loading working in rotation at each point of the structure. We conclude then that the internal rotation is zero, i.e. 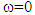 on
on 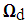 . The translation by cons remains possible, as we have noticed in [2] [3] [4] [5].Taking into account this remark, the energy of the medium (5) is simplified and it is writing so,
. The translation by cons remains possible, as we have noticed in [2] [3] [4] [5].Taking into account this remark, the energy of the medium (5) is simplified and it is writing so,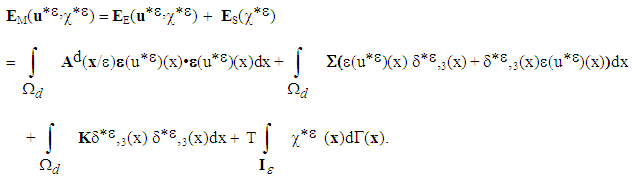 | (6) |
3. Energy Study of the Medium of a Composite Structure
- The reader is aware of the difficulty of the problem, the debonding can pre-exist before application of a loading and the energy of medium can intervene more displacement fields. In adopting always the couple notation, and taking into account (2) and (6), the problem consist to find the couple of fields
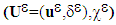 minimizing the energy of medium,
minimizing the energy of medium,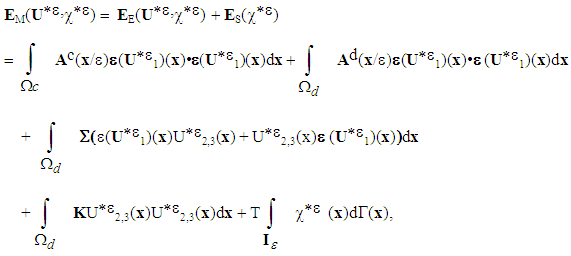 | (7) |
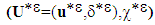 .We see that the problem is well complex: even if we manage to construct a minimizing sequence, it can do not converge in the right "space", since a sequence of characteristic functions do not necessarily converge towards a characteristic function (representative of a state of debonding). Therefore, the couple of solution field, if it exists can do not be "admissible". So we do not try to solve the problem in all its generality but at given surface energy (fixed). We calculate the elastic energy of the composite structure for different possible cases of decohesions [1] [2] [3] [13], for reject the figure cases, least envigeables, within the meaning of the adopted criterion. To do this, we "class" first, the states of decohesion of the composite structure according to geometrical criteria (volume defects, surface defects, lineal defects or punctual defects). As the surface energy varies only according to the "surface" of total debonding (or "total length" in the case of a fibred composite), we will define, for each type of debonding, the subclasses differentiated by their order greatness, in
.We see that the problem is well complex: even if we manage to construct a minimizing sequence, it can do not converge in the right "space", since a sequence of characteristic functions do not necessarily converge towards a characteristic function (representative of a state of debonding). Therefore, the couple of solution field, if it exists can do not be "admissible". So we do not try to solve the problem in all its generality but at given surface energy (fixed). We calculate the elastic energy of the composite structure for different possible cases of decohesions [1] [2] [3] [13], for reject the figure cases, least envigeables, within the meaning of the adopted criterion. To do this, we "class" first, the states of decohesion of the composite structure according to geometrical criteria (volume defects, surface defects, lineal defects or punctual defects). As the surface energy varies only according to the "surface" of total debonding (or "total length" in the case of a fibred composite), we will define, for each type of debonding, the subclasses differentiated by their order greatness, in  , of their elements. We present then first below, some states models of decohesion that may have a composite structure.
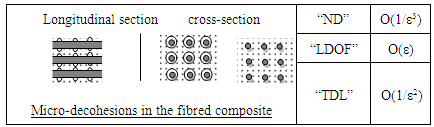
, of their elements. We present then first below, some states models of decohesion that may have a composite structure.3.1. Composites with Long Fibers
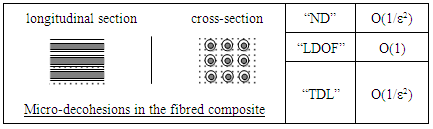
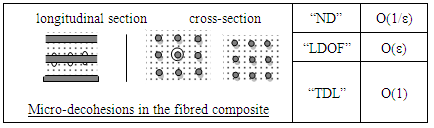
- In the following schemes, to saving space, we will note "ND" to designate "The Number of Decohesion", Likewise "LDOF" to designate "The Length of Decohesion in One Fiber" and finally "TDL" to designate "The Total Decohesion Length".
3.1.1. Volume Defects
- 1)
 2)
2)
3.1.2. Surface Defects
- 3)
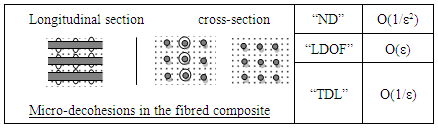 4)
4)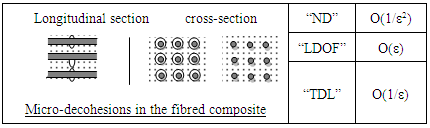
3.1.3. Linear Defects
- 5)
 6)
6)
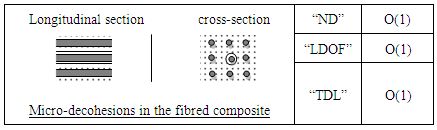
3.1.4. Punctual Defects
- 7)
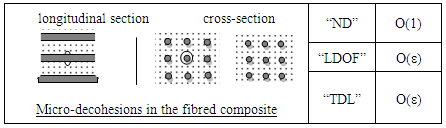
3.2. Laminate Composites
3.2.1. Volume Defects
- 8)
 9)
9)
3.2.2. Surface Defects
- 10)
 11)
11)
3.2.3. Linear Defects
- 12)
 13)
13)
3.2.4. Punctual Defects
- 14)
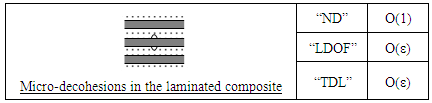
4. Quantitative Analysis of the Obtained Results
- If the purpose of this paper is to give, in summary, a few orders of magnitude of the elastic energy corresponding at some states of decohesion presented above, to deduce which states of decohesion should be rejected, in sense of the Francfort and Marigo minimization criterion, we endeavor nevertheless not to lose sight of the generic character of the methods used (Homogenization and matched asymptotic expansions), in computing of macroscopic behavior, that allows analyzing complex situations, in particular taking account, at the macroscopic level, of the presence of micro-defects in the homogenized composite structures. In the few studies conducted i.e., cases of figure numbers 1, 2, 3 and the states of decohesion numbers 9, 10 and 11 (see [2] [3] [6]), we deduce the following points:
4.1. Influence of Composites Type
- The effective behavior of a composite structure having periodic decohesions differs according to whether it is a laminate composite or a fibered composite. Indeed, the kinematics of the medium is described by two macroscopic displacement fields
 and
and 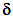 (one field only in the existing literature, see [20]). For a fibered composite, the translation is given by
(one field only in the existing literature, see [20]). For a fibered composite, the translation is given by 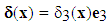 see [2]). For a laminated composite, it is given by,
see [2]). For a laminated composite, it is given by, 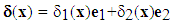 (see [3]). The scalar field
(see [3]). The scalar field 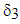 , defined on
, defined on 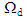 , is interpreted as the longitudinal relative sliding of the fibers compared to the matrix, the fields
, is interpreted as the longitudinal relative sliding of the fibers compared to the matrix, the fields 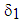 and
and 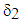 , when at them, are the two components of a planar field representing the slip of steep layers (inclusions) compared to soft layers (matrix).
, when at them, are the two components of a planar field representing the slip of steep layers (inclusions) compared to soft layers (matrix).4.2. Influence of Defects Type
- The methods used to modeling the damaged composite structures differ according to the type of the latter. For example, to study the cases of figure 1, 2 and 9, we use the periodic homogenization method. Another method, called matched asymptotic expansions [1] [24], was illustrated for the states of debonding numbers 3, 10, and 11. In addition, the effectif behavior of a such composite (with debonded constituents) differs from one case to another. Indeed, for the illustrative case number 1, the effective behavior is similar to a continuous medium whose kinematics is described by a single displacement field, and whose equilibrium is governed by classical three-dimensional equilibrium equations [19]. By cons, for the states of decohesion numbers 2 and 9, the kinematics is described by several displacement fields, and the equilibrium is governed by coupled equations, i.e., three-dimensional equilibrium equations and equations of beam type [2] (in the case of figure number 2, "fibered composite") or plate type[3] (in the case of figure number 9, "laminate composite"). For the cases of figure numbers 5, 11 and 12 (see [1] [6] [24]), although there have micro-defects, they have not influence, in first approximation, on the macroscopic behavior of the structure. It is not the same for the cases of decohesion numbers 2, 9 and 10, where the influence of the macroscopic debonding is felt from the first order.
4.3. Influence of Contact Laws
- The effective behavior of composite materials at debonded constituents depends on the contact law to imposing on the interfaces. For example, for a laminate, the kinematics of the equivalent structure is described by two displacement fields, a displacement field of the matrix
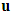 and a inner slip field
and a inner slip field 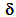 . If one authorizes the debonded interfaces to sliding without rubbing, while staying in contact, the internal sliding field is written as follow,
. If one authorizes the debonded interfaces to sliding without rubbing, while staying in contact, the internal sliding field is written as follow, 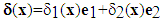 . But in the case without contact, it is written,
. But in the case without contact, it is written, 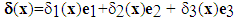 . It is seen well that the macroscopic behavior of such a composite is not the same if one changes the contact law to impose on the debonded interfaces and it was noticed, in the expression (4), for fibred composites.
. It is seen well that the macroscopic behavior of such a composite is not the same if one changes the contact law to impose on the debonded interfaces and it was noticed, in the expression (4), for fibred composites.5. Qualitative Analysis of the Effective Behavior of Composite Materials
- Let us retake the notations to fix ideas, and let us consider a unitary three-dimensional composite structure comprising n fibers. Let
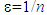 the parameter characterizing the microstructure, it also represents the dimensions of micro-defects (or micro-decohesions) that are of the order of
the parameter characterizing the microstructure, it also represents the dimensions of micro-defects (or micro-decohesions) that are of the order of 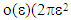 in surface for a "fibered composite" and
in surface for a "fibered composite" and 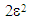 for a "laminate composite") [16]. It is assumed that, when they are present in the microstructure, they are "distributed" periodically, as indicated in the figures above. For the calculate of the orders of magnitude of the surface energies ES, we use the following two general rules:* For a fibered composite (fibers-matrix):
for a "laminate composite") [16]. It is assumed that, when they are present in the microstructure, they are "distributed" periodically, as indicated in the figures above. For the calculate of the orders of magnitude of the surface energies ES, we use the following two general rules:* For a fibered composite (fibers-matrix):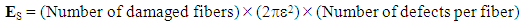 * For a laminate composite (folds stiffer/soft):
* For a laminate composite (folds stiffer/soft):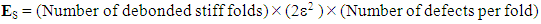 We present then, in the two tables below, the cases of figure studied, i.e., the states of debonding numbers 1, 2 and 3 for a fibered composite and the states of debonding numbers 9, 10 and 11 for a laminate composite. We give then the orders of magnitude, in
We present then, in the two tables below, the cases of figure studied, i.e., the states of debonding numbers 1, 2 and 3 for a fibered composite and the states of debonding numbers 9, 10 and 11 for a laminate composite. We give then the orders of magnitude, in 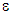 , of surface energies and energy restitution elastic (difference between the energy of the "healthy" composite structure and the elastic energy of the "debonded" composite structure) for each figure case studied. These energy restitutions are calculated in [2], [3], [6] and [24].
, of surface energies and energy restitution elastic (difference between the energy of the "healthy" composite structure and the elastic energy of the "debonded" composite structure) for each figure case studied. These energy restitutions are calculated in [2], [3], [6] and [24].
|
|
6. Discussion
- When a structure is subjected to an increasing loading, the structure is damaged (a crack appears). For a composite structure there is appearance of a debonding of its constituents. This debonding defines a decohesion state, solution of the energy minimization problem of Francfort and Marigo (Em=Es+Ee) among all possible fictitious decohesion states. We can say then that all other debonding states are rejected and cannot appear in this composite structure for this loading level. We see that the problem is well complex: we cannot compare all energies of all possible debonding states to find the state of debonding, solution of Francfort and Marigo problem. But we can conclude that a particular state of debonding cannot be a solution (i.e. it cannot appear in the structure) if we find a new state whose energy of medium is smaller. For the states whose energies of surface Es are the same (same order of magnitude) we compare their elastic energy Ee. This is the case for example of the states 1 and 2 and then 10 and 11 of above Tables 1 and 2. The state 10 is rejected in front of the state 11 because the order of magnitude of its elastic energy (so of its energy of medium) is more great. By cons we cannot reject any of the states 1 and 2 because the orders of magnitude of their elastic energy are the same. We must calculate numerically their energy to conclude.It is therefore very interesting to know the solution of the energy minimization problem of Francfort and Marigo, posed on a composite structure, but it is also interesting to know whether such or such debonding cannot appear in this structure for a given loading level.For the initiation problem of debonding in healthy composite structures, it is possible to find numerically the solution of this problem, as well as study the propagation of this initiated debonding. Indeed, we first must make an unstructured mesh whose nodes will be "duplicated" so that we can open it to the needs (for calculation of the energy restitution elastic). Then, in the calculations, locate the state of decohesion "initiated" by the criterion of maximum stresses. Considering then all possible local decohesion states, we deduce the initiated decohesion state [8] [12]. We can then repeat the process for studying the propagation of decohesion as well initiated [22] [25].
7. Conclusions
- The energetic study of the composite structures make in this paper, based on the theory of Francfort and Marigo [9], consist primarily to reject, for a loading level and a given surface energy (in order of magnitude of
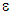 with
with 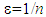 and where n denotes the number of fibers contained in the structure), the decohesions leading to a highest energies of medium. We can then reject a state of debonding, in doing so, but we can not "keep" some state; keep one state in the sense that it should be compared to another state of decohesion, to finally find the state of decohesion, solution of the minimization problem of Francfort and Marigo [9], because the states of decohesion are very numerous and we can not compare practically all these states. But the obtained results of this study are very interesting because it can be exploited in high tech industry to ensure that of this or that debonding can not appear in such composite pieces, subjected to loading of their use services.
and where n denotes the number of fibers contained in the structure), the decohesions leading to a highest energies of medium. We can then reject a state of debonding, in doing so, but we can not "keep" some state; keep one state in the sense that it should be compared to another state of decohesion, to finally find the state of decohesion, solution of the minimization problem of Francfort and Marigo [9], because the states of decohesion are very numerous and we can not compare practically all these states. But the obtained results of this study are very interesting because it can be exploited in high tech industry to ensure that of this or that debonding can not appear in such composite pieces, subjected to loading of their use services. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
