Yahya Berrehili, Abdelmoutalib Berrehili, Mohammed Rahmoune
Equipe de Modélisation & Simulation Numérique, Ecole Nationale des Sciences Appliquées d’Oujda, Université Mohamed 1er, Maroc
Correspondence to: Yahya Berrehili, Equipe de Modélisation & Simulation Numérique, Ecole Nationale des Sciences Appliquées d’Oujda, Université Mohamed 1er, Maroc.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
The present paper is devoted to an illustration of effective behavior on a classical torsion problem of a fiber-reinforced composite beam with debonded fibers but still in contact with the matrix. We show that the solution in displacement (which is given explicitly), of such problem, is independent on the microscopic variable and it is identical to that of a composite whose fibers are perfectly bonded to the matrix. It is not the same for the bending and traction problems where the associated solutions depend both on microscopic and macroscopic variable and which are different to that of a composite whose constituents are perfectly bonded. Consequently, the debonding of fibers in a composite beam but still in contact with the matrix has therefore not importance when and only when it comes to a torsional loading.
Keywords:
Homogenization, Composite beam, Debonded fibers, Modeling, Behavior, Torsion problem
Cite this paper: Yahya Berrehili, Abdelmoutalib Berrehili, Mohammed Rahmoune, Torsion of a Fiber-Reinforced Composite Beam with Debonded Fibers, International Journal of Mechanics and Applications, Vol. 6 No. 1, 2016, pp. 13-16. doi: 10.5923/j.mechanics.20160601.03.
1. Introduction
The use of unidirectional fiber-reinforced composite materials does not cease to grow in various domains and particularly in the domains of aerospace and aeronautics. This is due to their various properties and especially to their interesting mechanical behavior in terms of their specific effective stiffness in the direction of the fibers. The effective elastic behavior of such composites is now well known and well modeled by the homogenization theory as long as the fibers are assumed to be perfectly bonded to the matrix [1] [11-14]. By cons, not many studies have been made in the case where the constituents are debonded (see [8] [10] [15] [16] [17]). The results that we obtained in this last case are new and generals (see [3]). Specifically, the obtained effective behavior of a composite material in the case where the fibers are debonded but still in contact with the matrix is formally similar to a generalized continuous medium whose kinematics is not described only by the usual macroscopic displacement field but also a other displacement field describing the sliding of the fibers.The objective of this paper is therefore to illustrate this effective behavior, found in [3], on a classical elastostatic torsion problem of a fiber-reinforced composite beam. Although simple, the torsion problem, one of the three famous classical problems (traction/compression, bending and torsion), is of paramount importance for practical applications.The paper is organized as follows. The next section is devoted to the setting of the problem which consists to study the torsion problem of a fiber-reinforced composite beam with debonded fibers but still in contact with the matrix. The third section is devoted to a brief general recall of homogenization results obtained in [3] and adaptation of these results to our torsion problem of a “debonded” composite beam by formulating the homogenized problem associated with our torsion problem which consists to solve an equilibrium equations system (coupled and not classic). We solve therefore this system in the fourth section. And we end with a conclusion in the fifth section.
2. Problem Statement
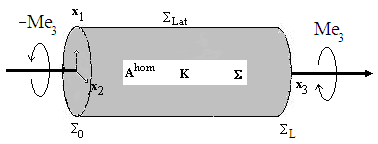
We study in this paper the torsion problem of a fiber-reinforced composite beam with debonded fibers. To do this, let us retake the example of the composite structure presented in [4] and [5] (for the traction and bending problems). The notations and the description of the “debonded” composite part are the same (see Figure 1.). It is a composite beam with a circular cross-section, of length L and radius R, and which the fibers are debonded but in contact with the matrix. We assume that in addition, the fibers can slide without friction (see [2] [3] [6]) for a torsion loading. The fibers and the matrix are assumed homogeneous, isotropic and having respectively the Lamé constants 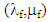 and
and 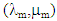 . No action is exerted on the lateral surface
. No action is exerted on the lateral surface 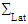 and the density of volumetric efforts f is assumed to be negligible. By cons, on both bases of the beam,
and the density of volumetric efforts f is assumed to be negligible. By cons, on both bases of the beam, 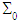 and
and 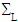 , are exerted surface efforts forming a torsional torque. More specifically on
, are exerted surface efforts forming a torsional torque. More specifically on 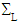 , they form an equivalent torsor to the given torque Me3, and on
, they form an equivalent torsor to the given torque Me3, and on 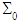 they form an equivalent torsor to the torque Me3. Therefore, M defines a torsional torque applied on the composite beam. This torque can be achieved by imposing, instead of these surface forces defined on
they form an equivalent torsor to the torque Me3. Therefore, M defines a torsional torque applied on the composite beam. This torque can be achieved by imposing, instead of these surface forces defined on 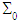 et
et 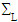 , the following conditions (in displacements and in stresses):
, the following conditions (in displacements and in stresses):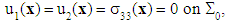 | (1) |
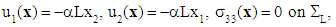 | (2) |
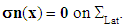 | (3) |
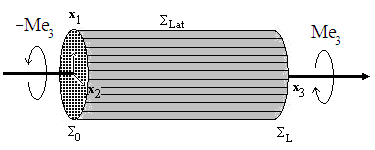 | Figure 1. The composite beam with debonded fibers |
Specifically, the torsional problem of the composite beam with debonded fibers but in contact with the matrix, thus defined, is formulated as follows: it is to seek the displacement field 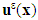 and the associated stress field
and the associated stress field 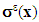 , solutions of the following torsion problem:
, solutions of the following torsion problem: 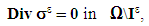 | (4) |
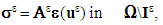 | (5) |
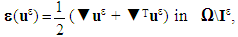 | (6) |
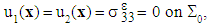 | (7) |
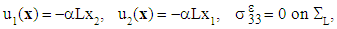 | (8) |
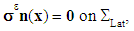 | (9) |
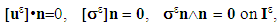 | (10) |
Let us adopt the following notations: 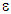 is a parameter related to the microstructure of the composite beam (report of the period by the length L of the beam, assumed small enough), Div being the divergence of a tensor (here it is the stress tensor
is a parameter related to the microstructure of the composite beam (report of the period by the length L of the beam, assumed small enough), Div being the divergence of a tensor (here it is the stress tensor 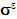 ),
), 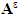 indicates the linear elasticity tensor of the composite beam,
indicates the linear elasticity tensor of the composite beam, 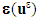 the strain field associated with the displacement field
the strain field associated with the displacement field 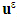 , n the outer normal of
, n the outer normal of 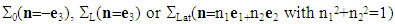 and
and 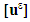 the jump or discontinuity of the displacement field
the jump or discontinuity of the displacement field 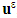 across the interface
across the interface 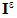 (reunion of all debonded interfaces, fibers-matrix). The three relations of the last line (10), reflect the continuity of the normal displacement field, the continuity of the stresses vector and the nullity of the shear on the debonded interfaces
(reunion of all debonded interfaces, fibers-matrix). The three relations of the last line (10), reflect the continuity of the normal displacement field, the continuity of the stresses vector and the nullity of the shear on the debonded interfaces 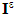 . Ω being the open domain of IR3 occupied by the composite beam.
. Ω being the open domain of IR3 occupied by the composite beam.
3. The Macroscopic Problem
As has been shown in [2] and [3], because of the debonding of fibers from the matrix, the first term u0 of the asymptotic development 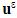 depends both on macroscopic variable x and microscopic variable
depends both on macroscopic variable x and microscopic variable 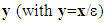 , in contrast to what one found in the existent literature where this field depends only on the macroscopic variable x (as in [7] [9] [10] and [15] [16] [17]). Therefore new macroscopic fields come into play in the effective kinematic of the composite structure. Specifically, the kinematic is described not only by a classical vector field u, representing the displacement of the matrix, but also by a new scalar field noted
, in contrast to what one found in the existent literature where this field depends only on the macroscopic variable x (as in [7] [9] [10] and [15] [16] [17]). Therefore new macroscopic fields come into play in the effective kinematic of the composite structure. Specifically, the kinematic is described not only by a classical vector field u, representing the displacement of the matrix, but also by a new scalar field noted 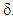 , interpreted as the relative sliding of the fibers relative to the matrix (it is also called, internal sliding of the composite structure).The first term u0(x,y) of the asymptotic expansion [1] of
, interpreted as the relative sliding of the fibers relative to the matrix (it is also called, internal sliding of the composite structure).The first term u0(x,y) of the asymptotic expansion [1] of 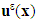 is then written, as in [4] and [5]:
is then written, as in [4] and [5]: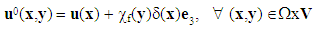 | (11) |
where 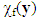 , with
, with 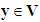 , is the characteristic function of Vf (equal to 1 on Vf and 0 on Vm).
, is the characteristic function of Vf (equal to 1 on Vf and 0 on Vm). 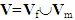 (reunion of the part fiber Vf and the part matrix Vm) is the basic cell associated with the composite beam (see Figure 2.).
(reunion of the part fiber Vf and the part matrix Vm) is the basic cell associated with the composite beam (see Figure 2.).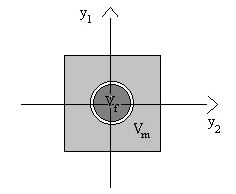 | Figure 2. The base cell V=Vf∪Vm |
And the couple of fields 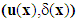 is a solution of a coupled elasticity problem, posed on an equivalent homogeneous structure (see Figure 3.), having as tensor of homogenized elasticity Ahom (calculated in [3] on the basic cell V):
is a solution of a coupled elasticity problem, posed on an equivalent homogeneous structure (see Figure 3.), having as tensor of homogenized elasticity Ahom (calculated in [3] on the basic cell V):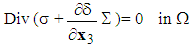 | (12) |
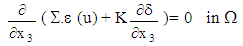 | (13) |
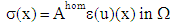 | (14) |
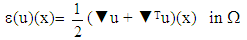 | (15) |
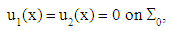 | (16) |
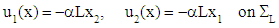 | (17) |
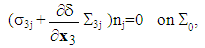 | (18) |
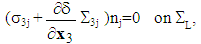 | (19) |
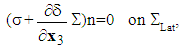 | (20) |
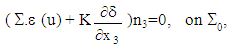 | (21) |
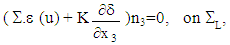 | (22) |
The homogenized problem thus defined is a system of equilibrium equations coupled non-classical: it contains additionally of homogenized tensor Ahom (of the composite structure) new homogenized tensors K and 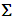 . K is interpreted as the effective stiffness tensor in extension of the debonded fibers and
. K is interpreted as the effective stiffness tensor in extension of the debonded fibers and 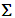 as an effective stress tensor. These two tensors are calculated in [3] by solving new cell problems ignored in the existent literature. They appear in the homogenized problem equations by coupling the two displacement fields u and
as an effective stress tensor. These two tensors are calculated in [3] by solving new cell problems ignored in the existent literature. They appear in the homogenized problem equations by coupling the two displacement fields u and 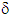 .
. | Figure 3. The homogenized composite beam |
4. The Displacement Field Solution
We verify that the proposed couple of displacements field 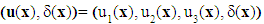 defined explicitly by:
defined explicitly by: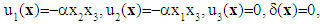 | (23) |
where 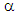 is a given real constant, defining the rotation angle imposed on the bases
is a given real constant, defining the rotation angle imposed on the bases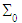 and
and 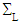 , define well a solution of the torsion problem above (12)-(22). Indeed, first note that
, define well a solution of the torsion problem above (12)-(22). Indeed, first note that 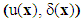 is a kinematically admissible field, i.e. it verifies well the boundary conditions (16) and (17) of the problem (12)-(22). Furthermore, the deformation tensor corresponding to the displacement field u(x) is defined as follows:
is a kinematically admissible field, i.e. it verifies well the boundary conditions (16) and (17) of the problem (12)-(22). Furthermore, the deformation tensor corresponding to the displacement field u(x) is defined as follows: 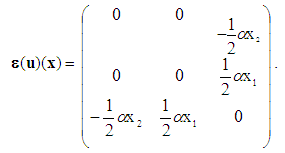 | (24) |
According to the law of behavior (14), the stress tensor 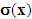 is written as follow:
is written as follow: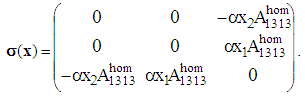 | (25) |
The reader can easily verify, taking into account (23)4 i.e.  , that the stress field (25) satisfies well the static equilibrium equation (12) and the boundary conditions (18), (19) and (20), imposed on
, that the stress field (25) satisfies well the static equilibrium equation (12) and the boundary conditions (18), (19) and (20), imposed on . The equilibrium equations (13), indexed by (x1,x2), and the conditions (21) and (22), imposed on
. The equilibrium equations (13), indexed by (x1,x2), and the conditions (21) and (22), imposed on 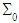 et
et 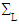 , are also satisfied because of (23)4, (24) and the fact that only the terms
, are also satisfied because of (23)4, (24) and the fact that only the terms 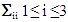 are nonzero (
are nonzero (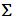 being the tensor resulting internal stresses generated in the basic cell by an internal extension of the fiber, calculated in [3]).Remark: If (P;e1,e2,e3) is the local orthonormal reference associated, in point P, to cylindrical coordinates r,
being the tensor resulting internal stresses generated in the basic cell by an internal extension of the fiber, calculated in [3]).Remark: If (P;e1,e2,e3) is the local orthonormal reference associated, in point P, to cylindrical coordinates r, 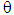 and z, one has on
and z, one has on 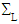 :
: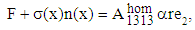 | (26) |
and the torsor of efforts defined by the surface force density (26) on 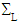 is well a torque of axis Ox3 and of moment Me3, with:
is well a torque of axis Ox3 and of moment Me3, with: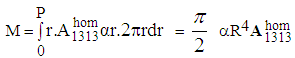 | (27) |
The torsion torque M is proportional to the torsion unit angle 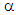 of the cylinder:
of the cylinder: 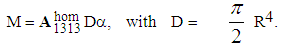 | (28) |
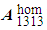 D is by definition the modulus of rigidity in torsion of the cylinder; it is the product of the stiffness modulus at shear
D is by definition the modulus of rigidity in torsion of the cylinder; it is the product of the stiffness modulus at shear 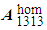 by a factor D, of geometrical nature, that is no other here that the moment of inertia of the circular section with respect to the axis Ox3, assumed constant basis weight and equal to unity. The effect of debonding of fibers is felt in the report between the moment M to exercise and the torsion angle
by a factor D, of geometrical nature, that is no other here that the moment of inertia of the circular section with respect to the axis Ox3, assumed constant basis weight and equal to unity. The effect of debonding of fibers is felt in the report between the moment M to exercise and the torsion angle 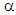 . This report involves the homogenized coefficient
. This report involves the homogenized coefficient 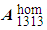 of the debonded composite beam, which is strictly smaller than that of a composite beam whose fibers are perfectly bonded (see [3]).
of the debonded composite beam, which is strictly smaller than that of a composite beam whose fibers are perfectly bonded (see [3]).
5. Conclusions
The couple 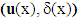 defined by (23) is a solution of the homogenized problem (12)-(22). The displacement field defined by (11) is therefore solution of the torsion problem (4)-(10). Any other solution is obtained by adding to the expression (11) a rigid displacement field considered unimportant for the envisaged mechanical. This solution is identical to that of a composite whose constituents are perfectly bonded (because
defined by (23) is a solution of the homogenized problem (12)-(22). The displacement field defined by (11) is therefore solution of the torsion problem (4)-(10). Any other solution is obtained by adding to the expression (11) a rigid displacement field considered unimportant for the envisaged mechanical. This solution is identical to that of a composite whose constituents are perfectly bonded (because 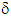 is zero), unlike those of the problems of bending and traction (see [4] and [5]) where the field
is zero), unlike those of the problems of bending and traction (see [4] and [5]) where the field 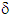 is nonzero. The debonding of fibers in a composite beam but still in contact with the matrix has therefore not importance only and only where it is of a torsional loading.
is nonzero. The debonding of fibers in a composite beam but still in contact with the matrix has therefore not importance only and only where it is of a torsional loading.
References
| [1] | A. Bensoussan, J.-L. Lions, G. Papanicolaou, "Asymptotic Analysis of Periodic Structures", North Holland, 1978. |
| [2] | Y. Berrehili, J.-J. Marigo, "Modélisation en 2D du comportement d'un composite fibré à constituants décollés", Physical and Chemical News, 53 10-14, 2010. |
| [3] | Y. Berrehili, J.-J. Marigo, "The homogenized behavior of unidirectional fiber-reinforced composite materials in the case of debonded fibers", Mathematics and Mechanics of Complex Systems. vol. 2, n° 2, 181-207, 2014. |
| [4] | Y. Berrehili, "Longitudinal traction of fiber-reinforced composite beam with debonded fibers", International Journal of theoretical and mathematical physics, 4(2): 53-57, 2014. |
| [5] | Y. Berrehili, "Bending of fiber-reinforced composite beam with debonded fibers", International Journal of Composite Materials, 4(2): 130-134, 2014. |
| [6] | Y. Berrehili, "The effective behavior of laminated composite materials in the case of debonded folds", International Journal of Composite Materials, 4(2): 45-51, 2014. |
| [7] | A. Brillard, M. El Jarroudi, "Asymptotic behaviour of a cylindrical elastic structure periodically reinforced along identical fibres", IMA J. Appl. Math. 66 567-590, 2001. |
| [8] | A. Caporale, R. Luciano, E. Sacco, "Micromechanical analysis of interfacial debonding in unidirectional fiber- reinforced composites", Comput. Struct., 84 2200-2211, 2006. |
| [9] | G. Chatzigeorgiou, N. Charalambakis, F. Murat, "Homogenization problems of a hollow cylinder made of elastic materials with discontinuous properties", International Journal of Solids and Structures, 45 5165-5180, 2008. |
| [10] | P. Gruber, "FETI-based Homogeneization of composites with perfect bonding and debonding of constituents" Bulletin of Applied Mechanics, 4 11-17, 2008. |
| [11] | F. Léné, "Contribution à l'étude des matériaux composites et de leur endommagement", Thèse de Doctorat d'Etat, Université Pierre et Marie Curie, Paris, 1984. |
| [12] | J.-C. Michel, H. Moulinec, and P. Suquet, "Effective properties of composite materials with periodic microstructure: a computational approach. Comput. Meth. Appl. Mech. Eng. 172, 109-143, 1999. |
| [13] | E. Sanchez-Palencia, "Non homogeneous media and vibration theory", n° 127 in Lecture Notes in Physics, Berlin: Springer, 1980. |
| [14] | P. Suquet, "Plasticité et homogénéisation", Thèse de Doctorat d'Etat, Université Pierre et Marie Curie, Paris, 1982. |
| [15] | H. Teng, Transverse stiffness properties of unidirectional fiber composites containing debonded fibers. Composites: part A. 38, 682-690, (2007). |
| [16] | H. Teng, "Stiffness properties of particulate composites containing debonded particules", International Journal of Solids and Structures, 47 2191-2200, 2010. |
| [17] | YH Zhao, GJ Weng, "The effect of debonding angle on the reduction of effective modull of particule and fiber-reinforced composites", J. Appl. Mech., 69 292-302, 2002. |



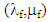 and
and 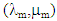 . No action is exerted on the lateral surface
. No action is exerted on the lateral surface 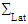 and the density of volumetric efforts f is assumed to be negligible. By cons, on both bases of the beam,
and the density of volumetric efforts f is assumed to be negligible. By cons, on both bases of the beam, 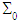 and
and 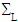 , are exerted surface efforts forming a torsional torque. More specifically on
, are exerted surface efforts forming a torsional torque. More specifically on 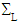 , they form an equivalent torsor to the given torque Me3, and on
, they form an equivalent torsor to the given torque Me3, and on 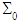 they form an equivalent torsor to the torque Me3. Therefore, M defines a torsional torque applied on the composite beam. This torque can be achieved by imposing, instead of these surface forces defined on
they form an equivalent torsor to the torque Me3. Therefore, M defines a torsional torque applied on the composite beam. This torque can be achieved by imposing, instead of these surface forces defined on 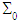 et
et 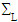 , the following conditions (in displacements and in stresses):
, the following conditions (in displacements and in stresses):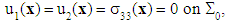
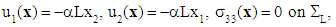
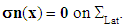

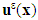 and the associated stress field
and the associated stress field 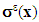 , solutions of the following torsion problem:
, solutions of the following torsion problem: 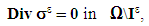
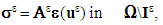
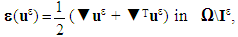
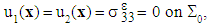
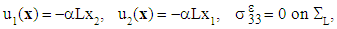
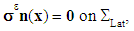
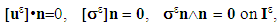
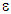 is a parameter related to the microstructure of the composite beam (report of the period by the length L of the beam, assumed small enough), Div being the divergence of a tensor (here it is the stress tensor
is a parameter related to the microstructure of the composite beam (report of the period by the length L of the beam, assumed small enough), Div being the divergence of a tensor (here it is the stress tensor 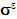 ),
), 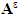 indicates the linear elasticity tensor of the composite beam,
indicates the linear elasticity tensor of the composite beam, 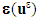 the strain field associated with the displacement field
the strain field associated with the displacement field 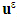 , n the outer normal of
, n the outer normal of 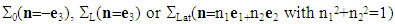 and
and 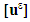 the jump or discontinuity of the displacement field
the jump or discontinuity of the displacement field 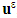 across the interface
across the interface 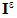 (reunion of all debonded interfaces, fibers-matrix). The three relations of the last line (10), reflect the continuity of the normal displacement field, the continuity of the stresses vector and the nullity of the shear on the debonded interfaces
(reunion of all debonded interfaces, fibers-matrix). The three relations of the last line (10), reflect the continuity of the normal displacement field, the continuity of the stresses vector and the nullity of the shear on the debonded interfaces 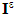 . Ω being the open domain of IR3 occupied by the composite beam.
. Ω being the open domain of IR3 occupied by the composite beam.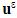 depends both on macroscopic variable x and microscopic variable
depends both on macroscopic variable x and microscopic variable 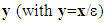 , in contrast to what one found in the existent literature where this field depends only on the macroscopic variable x (as in [7] [9] [10] and [15] [16] [17]). Therefore new macroscopic fields come into play in the effective kinematic of the composite structure. Specifically, the kinematic is described not only by a classical vector field u, representing the displacement of the matrix, but also by a new scalar field noted
, in contrast to what one found in the existent literature where this field depends only on the macroscopic variable x (as in [7] [9] [10] and [15] [16] [17]). Therefore new macroscopic fields come into play in the effective kinematic of the composite structure. Specifically, the kinematic is described not only by a classical vector field u, representing the displacement of the matrix, but also by a new scalar field noted 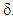 , interpreted as the relative sliding of the fibers relative to the matrix (it is also called, internal sliding of the composite structure).The first term u0(x,y) of the asymptotic expansion [1] of
, interpreted as the relative sliding of the fibers relative to the matrix (it is also called, internal sliding of the composite structure).The first term u0(x,y) of the asymptotic expansion [1] of 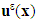 is then written, as in [4] and [5]:
is then written, as in [4] and [5]: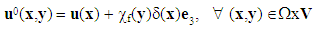
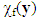 , with
, with 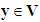 , is the characteristic function of Vf (equal to 1 on Vf and 0 on Vm).
, is the characteristic function of Vf (equal to 1 on Vf and 0 on Vm). 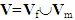 (reunion of the part fiber Vf and the part matrix Vm) is the basic cell associated with the composite beam (see Figure 2.).
(reunion of the part fiber Vf and the part matrix Vm) is the basic cell associated with the composite beam (see Figure 2.).
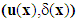 is a solution of a coupled elasticity problem, posed on an equivalent homogeneous structure (see Figure 3.), having as tensor of homogenized elasticity Ahom (calculated in [3] on the basic cell V):
is a solution of a coupled elasticity problem, posed on an equivalent homogeneous structure (see Figure 3.), having as tensor of homogenized elasticity Ahom (calculated in [3] on the basic cell V):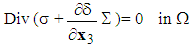
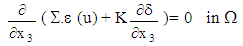
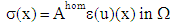
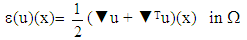
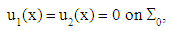
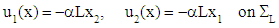
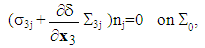
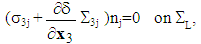
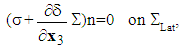
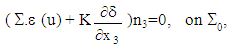
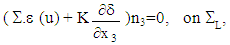
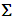 . K is interpreted as the effective stiffness tensor in extension of the debonded fibers and
. K is interpreted as the effective stiffness tensor in extension of the debonded fibers and 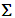 as an effective stress tensor. These two tensors are calculated in [3] by solving new cell problems ignored in the existent literature. They appear in the homogenized problem equations by coupling the two displacement fields u and
as an effective stress tensor. These two tensors are calculated in [3] by solving new cell problems ignored in the existent literature. They appear in the homogenized problem equations by coupling the two displacement fields u and 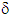 .
.
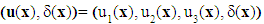 defined explicitly by:
defined explicitly by: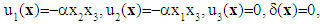
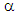 is a given real constant, defining the rotation angle imposed on the bases
is a given real constant, defining the rotation angle imposed on the bases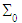 and
and 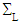 , define well a solution of the torsion problem above (12)-(22). Indeed, first note that
, define well a solution of the torsion problem above (12)-(22). Indeed, first note that 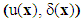 is a kinematically admissible field, i.e. it verifies well the boundary conditions (16) and (17) of the problem (12)-(22). Furthermore, the deformation tensor corresponding to the displacement field u(x) is defined as follows:
is a kinematically admissible field, i.e. it verifies well the boundary conditions (16) and (17) of the problem (12)-(22). Furthermore, the deformation tensor corresponding to the displacement field u(x) is defined as follows: 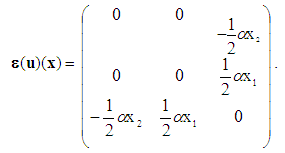
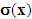 is written as follow:
is written as follow: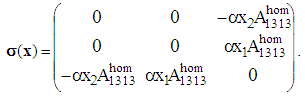
 , that the stress field (25) satisfies well the static equilibrium equation (12) and the boundary conditions (18), (19) and (20), imposed on
, that the stress field (25) satisfies well the static equilibrium equation (12) and the boundary conditions (18), (19) and (20), imposed on . The equilibrium equations (13), indexed by (x1,x2), and the conditions (21) and (22), imposed on
. The equilibrium equations (13), indexed by (x1,x2), and the conditions (21) and (22), imposed on  et
et 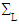 , are also satisfied because of (23)4, (24) and the fact that only the terms
, are also satisfied because of (23)4, (24) and the fact that only the terms 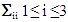 are nonzero (
are nonzero (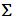 being the tensor resulting internal stresses generated in the basic cell by an internal extension of the fiber, calculated in [3]).Remark: If (P;e1,e2,e3) is the local orthonormal reference associated, in point P, to cylindrical coordinates r,
being the tensor resulting internal stresses generated in the basic cell by an internal extension of the fiber, calculated in [3]).Remark: If (P;e1,e2,e3) is the local orthonormal reference associated, in point P, to cylindrical coordinates r, 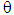 and z, one has on
and z, one has on 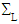 :
: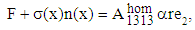
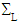 is well a torque of axis Ox3 and of moment Me3, with:
is well a torque of axis Ox3 and of moment Me3, with: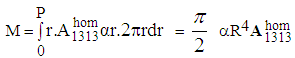
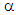 of the cylinder:
of the cylinder: 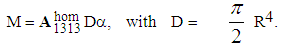
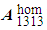 D is by definition the modulus of rigidity in torsion of the cylinder; it is the product of the stiffness modulus at shear
D is by definition the modulus of rigidity in torsion of the cylinder; it is the product of the stiffness modulus at shear 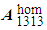 by a factor D, of geometrical nature, that is no other here that the moment of inertia of the circular section with respect to the axis Ox3, assumed constant basis weight and equal to unity. The effect of debonding of fibers is felt in the report between the moment M to exercise and the torsion angle
by a factor D, of geometrical nature, that is no other here that the moment of inertia of the circular section with respect to the axis Ox3, assumed constant basis weight and equal to unity. The effect of debonding of fibers is felt in the report between the moment M to exercise and the torsion angle 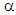 . This report involves the homogenized coefficient
. This report involves the homogenized coefficient 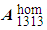 of the debonded composite beam, which is strictly smaller than that of a composite beam whose fibers are perfectly bonded (see [3]).
of the debonded composite beam, which is strictly smaller than that of a composite beam whose fibers are perfectly bonded (see [3]).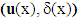 defined by (23) is a solution of the homogenized problem (12)-(22). The displacement field defined by (11) is therefore solution of the torsion problem (4)-(10). Any other solution is obtained by adding to the expression (11) a rigid displacement field considered unimportant for the envisaged mechanical. This solution is identical to that of a composite whose constituents are perfectly bonded (because
defined by (23) is a solution of the homogenized problem (12)-(22). The displacement field defined by (11) is therefore solution of the torsion problem (4)-(10). Any other solution is obtained by adding to the expression (11) a rigid displacement field considered unimportant for the envisaged mechanical. This solution is identical to that of a composite whose constituents are perfectly bonded (because 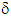 is zero), unlike those of the problems of bending and traction (see [4] and [5]) where the field
is zero), unlike those of the problems of bending and traction (see [4] and [5]) where the field 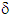 is nonzero. The debonding of fibers in a composite beam but still in contact with the matrix has therefore not importance only and only where it is of a torsional loading.
is nonzero. The debonding of fibers in a composite beam but still in contact with the matrix has therefore not importance only and only where it is of a torsional loading. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML