-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Mechanics and Applications
p-ISSN: 2165-9281 e-ISSN: 2165-9303
2015; 5(1): 16-22
doi:10.5923/j.mechanics.20150501.03
The Transient Electromagnetic Field Created by Electric Line Source on a Plane Conducting Earth
Ghada M. Sami 1, 2, Fatimah A. Al-Najim 1
1Mathematicsand Statistics Department, Faculty of Science, King Faisal University, KSA
2Mathematics Department, Faculty of Science, Ain shams University, Cairo, Egypt
Correspondence to: Ghada M. Sami , Mathematicsand Statistics Department, Faculty of Science, King Faisal University, KSA.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
The transient electromagnetic field of an electric line source on a two-layer earth model can be expressed in analytical form. To derive closed-form expressions for the fields anywhere on a two-layer earth, the modified Cagniard method is used. This method is used to perform the numerical calculation of the electric field for different points of excitation and observation on the earth, as well as for different values of the earth`s conductivity and permittivity. The numerical results will be presented graphically for the transient electromagnetic field for various values of the permittivity and electrical conductivities of the two layers. The effect of the conductivity is of significant importance for the calculation to get the transient electromagnetic field on a plane conducting earth.
Keywords: Electromagnetic field, Transient analysis
Cite this paper: Ghada M. Sami , Fatimah A. Al-Najim , The Transient Electromagnetic Field Created by Electric Line Source on a Plane Conducting Earth, International Journal of Mechanics and Applications, Vol. 5 No. 1, 2015, pp. 16-22. doi: 10.5923/j.mechanics.20150501.03.
Article Outline
1. Introduction
- Several experimental and theoretical models have been studied the electromagnetic transients. In early 1969, T.T. Wu [1] stated: “It is worth emphasizing that our knowledge about the transient response of the antennas is very meager indeed. Any progress in this rather neglected field is certainly going to be of a tremendous value”. Now, the literature on this subject is vast. Some of these studies are motivated by the desire to provide adequate protection of electronic equipment in a strong electromagnetic pulse (EMP) (Vance [2]). Other studies have been applied to the probing of the fields in geological media (Wait [3]), determination of the current in a lightning return stroke (Uman and Lain [4]), the detection of nuclear bursts (Johler [5]), and the discrimination of a radar scatterer (Moffatt and Mains [6]). In this paper will study the problem of the transient electromagnetic field of an electric line source on a two layered conducting earth. Furthermore, we will focus on the effects caused by the presence of the earth’s surface. A classical work in this area is that of Van der Pol [7] for the transient field over a non-conducting earth generated by a vertical dipole source situated in the interface between the air and the earth. The transient solution of an elevated dipole was also obtained by Van der Pol and Levelt [8] and Bremmer [9]. Wait [10, 11] and Novikov [12] studied the transient response of a vertical dipole with a step or ramp function current source over a finitely conducting earth. Since the Sommerfeld-Norton ground wave expansion is employed, which is valid for a distance large enough compared with the free space wavelength, their results are expected to be accurate mainly in the very early time portion of the response. Approximate expression for the transient field at later observation times was found by Chang [13] and Wait [14] under the assumption that the dissipative half-space can be replaced by an impedance surface.However, an attractive alternative is furnished by De Hoop [15] modificationn of Cagniard’s technique that found wide applications in the theory of seismic waves in Cagniard [16] and [17]. Also, few electromagnetic problems have been investigated along these lines (De Hoop and Frankena [18] and Langenberg [19]). Kooij [20] and [21] studied the transient electromagnetic field of a pulsed vertical magnetic dipole above a conducting earth, and of an electric line source above a plane drude model plasmatic half-space, these showed that it is possible to arrive to a representation for the field in the transform domain that allows the application of the Cagniard-De Hoop method.Kuester [22] investigated the transient reflected field of a pulsed line source over a conducting half-space. Bishay and Sami [23] expressed, in an analytical form the transient field in the time domain of a thin circular loop antenna on a two-layered conducting earth model. Sami [24] calculated the influence of a magnetically permeable surface layer on transient electromagnetic field of a vertical magnetic dipole on a two-layer conducting earth.The aim of this paper is to drive a representation for the field in the transform domain that allows the application of the Cagniard-De Hoop method to obtain the transient reflected field in the form of a single finite integral. Of particular interest is the physical insight provided by the Cagniard-De Hoop method at each point in the configuration, the transient field is decomposed exactly into physical meaningful parts. Numerical results will be represented graphically for the electric field anywhere on a two layer earth for different values of the earth`s conductivity and permittivity.
2. Description of the Configuration
- We consider the electromagnetic field in the upper half space of two homogeneous, isotropic, semi-infinite media. To specify the position in the configuration, we employ the ؤartesian coordinates (x, y, z) with origin O and three mutually perpendicular base vectors (i, j, k) of unit length each. The upper medium occupies the half space 0 ≤ z < ∞, whereas the lower medium occupies the half space -∞ < z < 0, as Figure 1. The time coordinate is denoted by t, with tR. The electromagnetic properties are characterized by their permittivity
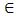 , permeability
, permeability 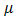 , and the electrical conductivity
, and the electrical conductivity 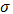 . The media are modeled according to the classical Maxwell model with constant permittivity, permeability and conductivity. For the upper medium we have,
. The media are modeled according to the classical Maxwell model with constant permittivity, permeability and conductivity. For the upper medium we have, 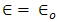 ,
, 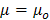 and
and 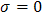 . For the lower medium, we have
. For the lower medium, we have 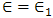 ,
, 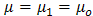 and
and 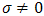 . An electric current line source starts to radiate at the instant t = 0, at the earth's surface.
. An electric current line source starts to radiate at the instant t = 0, at the earth's surface.3. Method of the Solution
- The electromagnetic field in the configuration is described in terms of the electric field strength E and the magnetic field strength H. the action of the source is characterized by specifying the volume density of its electric current J. In any domain where the field quantities are continuously differentiable, they satisfy the following electromagnetic field equations:
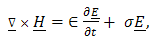 | (1) |
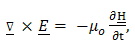 | (2) |
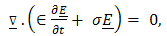 | (3) |
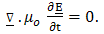 | (4) |
 , is the field that source world generate if no boundary were present.2 – The reflected field
, is the field that source world generate if no boundary were present.2 – The reflected field  is the difference between the total field in region0 ≤ Z < ∞ and the incident field.3 – The transmitted field
is the difference between the total field in region0 ≤ Z < ∞ and the incident field.3 – The transmitted field  which is the field in the region
which is the field in the region 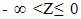 across the interface of the two media, the boundary conditions below hold,
across the interface of the two media, the boundary conditions below hold,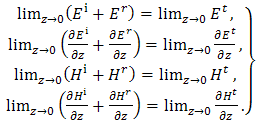 | (5) |
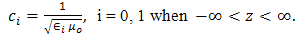 | (6) |
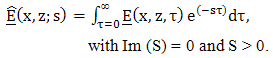 | (7) |
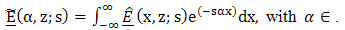 | (8) |
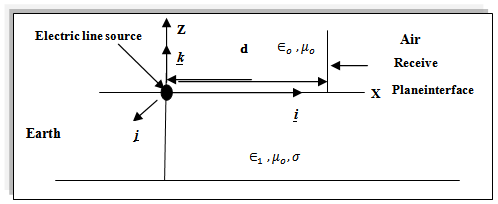 | Figure 1. Geometry of the problem |
- The inverse Fourier transformation,
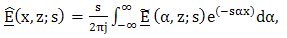 | (9) |
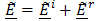 has been determined, the representation (9) is used to arrive at an expression for
has been determined, the representation (9) is used to arrive at an expression for 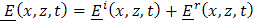 . This is accomplished by a specific scheme of transformations in the complex (∝) plane followed by an application of the uniqueness theorem of the one – sided Laplace transform (7).
. This is accomplished by a specific scheme of transformations in the complex (∝) plane followed by an application of the uniqueness theorem of the one – sided Laplace transform (7).4. Incident and Reflected Field Representations
- We take into account the two – dimensionality of the problem. To this end, we decompose each vectorial quantity in to a component that is parallel to the line source, this component is denoted by the subscript
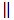 and a component in the plane perpendicular to it, this component is denoted by the subscript
and a component in the plane perpendicular to it, this component is denoted by the subscript 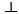 . Taking into account that
. Taking into account that  and
and 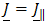 , we can rewrite the electromagnetic field equations (1)-(4) in a from where only an E- polarized field is generated for which
, we can rewrite the electromagnetic field equations (1)-(4) in a from where only an E- polarized field is generated for which 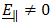 and
and 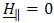 . In this section, we determine the representation of the type (9) for the incident and reflected field. The incident electromagnetic field satisfies Maxwell's equations (1)-(4) with
. In this section, we determine the representation of the type (9) for the incident and reflected field. The incident electromagnetic field satisfies Maxwell's equations (1)-(4) with 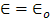 and
and 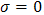 . For the localized line source of Figure 1, we have
. For the localized line source of Figure 1, we have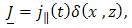 | (10) |
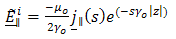 | (11) |
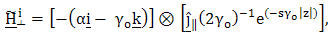 | (12) |
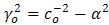 , when Re
, when Re 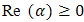 , and
, and 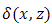 is the Dirac-delta function.Similarly, for the reflected field, we obtain the generated E-polarized field as
is the Dirac-delta function.Similarly, for the reflected field, we obtain the generated E-polarized field as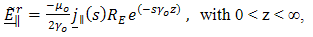 | (14) |
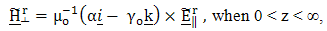 | (15) |
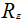 denotes the electric field reflection Factor for E – polarized waves. Applying the boundary condition (5), we obtain
denotes the electric field reflection Factor for E – polarized waves. Applying the boundary condition (5), we obtain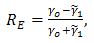 | (16) |
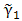 is given by
is given by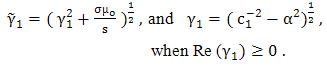 | (17) |
5. Integral Representation of the Reflection Factor
- In this section, the reflection factor RE is rewritten in the form of an integral representation such that the Cagniard-De Hoop technique can be applied. First, we multiply both the numerator and the denominator of RE with
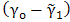 , then
, then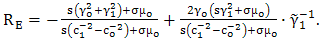 | (18) |
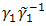 can be written as
can be written as 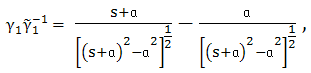 | (19) |
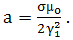 | (20) |
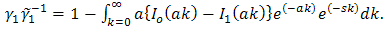 | (21) |
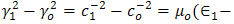
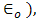 we obtain
we obtain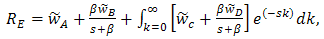 | (22) |
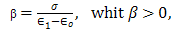 | (23) |
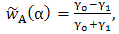 | (24) |
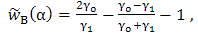 | (25) |
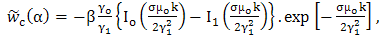 | (26) |
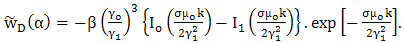 | (27) |
6. Time Domain Field Expressions
- By applying the inverse Fourier transformation (9) with respect tox to equation (14) and (15) together with equation (24–29), we obtain the corresponding expressions, which are of the form
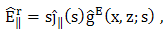 | (28) |
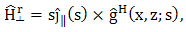 | (29) |
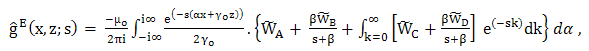 | (30) |
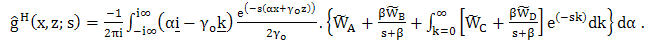 | (31) |
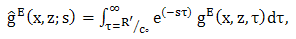 | (32) |
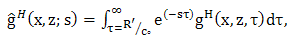 | (33) |
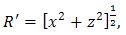 | (34) |
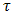 occur in the integration and where
occur in the integration and where 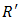 is the distance from the image of the electric line source to the point of observation. Now, we observe that
is the distance from the image of the electric line source to the point of observation. Now, we observe that 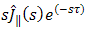 is the Laplace transform. Of a function of time that vanishes when
is the Laplace transform. Of a function of time that vanishes when 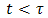 and equal
and equal 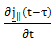 when
when 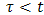 , for the fields
, for the fields 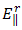 and
and 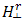 , hence, we get
, hence, we get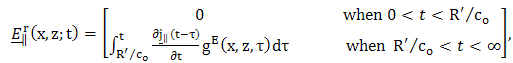 | (35) |
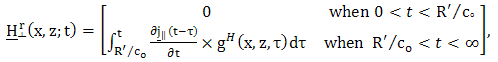 | (36) |
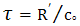
7. Cagniard – De Hoop Technique
- In this section, we will apply the cagniard – De Hoop technique in order to find an expression for
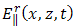 and
and 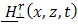 . In view of subsequent deformations of the path of integration, we take
. In view of subsequent deformations of the path of integration, we take 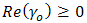 and
and 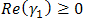 not only on the imaginary
not only on the imaginary 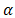 axis but everywhere in the complex
axis but everywhere in the complex 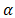 plane this implies that branch cuts are introduced along
plane this implies that branch cuts are introduced along 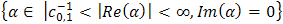 . Now, the path of integration in the complex
. Now, the path of integration in the complex 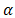 plane is deformed in a cagniard – De Hoop contour defined through,
plane is deformed in a cagniard – De Hoop contour defined through,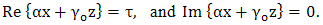 | (37) |
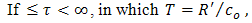 | (38) |
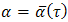 denote its parametric representation in the upper half of the complex α plan (i.e., {α∈⨕│-∞
denote its parametric representation in the upper half of the complex α plan (i.e., {α∈⨕│-∞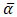 . By solving (37), we obtain
. By solving (37), we obtain 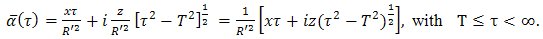 | (39) |
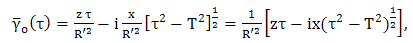 | (40) |
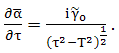 | (41) |
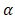 axis and reversing the orders of integration in order to apply the uniqueness argument of equation (32) – (36), we obtain,
axis and reversing the orders of integration in order to apply the uniqueness argument of equation (32) – (36), we obtain,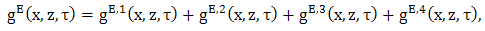 | (42) |
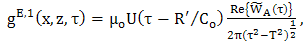 | (43) |
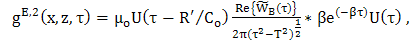 | (44) |
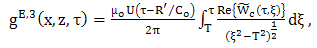 | (45) |
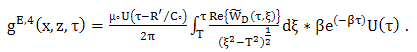 | (46) |
 by using equation (32) as
by using equation (32) as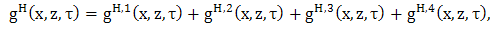 | (47) |
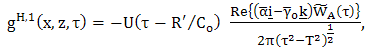 | (48) |
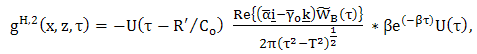 | (49) |
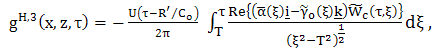 | (50) |
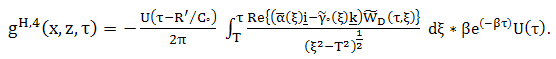 | (51) |
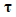 . Further, we have that
. Further, we have that 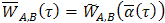 and
and 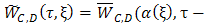
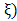 . Expressions (42) and (35) form the desired closed-form expression for the space-time reflected electric field and expressions (47) and (36) form the desired closed-form expression for the space-time reflected magnetic field. Further, it is easily verified in the expression (42) and (47), together with (43) - (51), that the terms
. Expressions (42) and (35) form the desired closed-form expression for the space-time reflected electric field and expressions (47) and (36) form the desired closed-form expression for the space-time reflected magnetic field. Further, it is easily verified in the expression (42) and (47), together with (43) - (51), that the terms  and
and 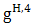 vanish if
vanish if 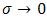 . In the final space-time expression of the reflected field, the convolution of the excitation function
. In the final space-time expression of the reflected field, the convolution of the excitation function 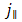 and the exponential function in (44), (46), (49), and (51) can be carried out analytically for various types of sources. The current in the electric line source is defined by:
and the exponential function in (44), (46), (49), and (51) can be carried out analytically for various types of sources. The current in the electric line source is defined by: 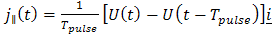 .In which U (t) is the Heaviside's unit step function,
.In which U (t) is the Heaviside's unit step function, 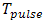 is the pulse duration and
is the pulse duration and 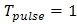 . The convolution of the source function
. The convolution of the source function 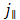 and the exponential function in (45), (47), (50) and (52) is carried out analytically. If
and the exponential function in (45), (47), (50) and (52) is carried out analytically. If 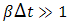 , where
, where 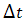 denotes the numerical time discretization step, we can approximate the function
denotes the numerical time discretization step, we can approximate the function 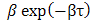 by a Dirac delta function, which simplifies the expression for gE(x, t).
by a Dirac delta function, which simplifies the expression for gE(x, t).8. Numerical Results and Discussion
- The transient electromagnetic field due to electric line source on a two-layer conducting earth can be expressed in analytical form. The normalized reflected fields have been calculated for different values of conductivity, and ratio of permittivity
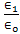 , at the two distance pointe (d = 1m and 10m) of observation and excitation. The results represented graphically and illustrated by Figure 2 [(a-e) and (f-j)]. These figures represent the normalized electric fieldfor different values of conductivity
, at the two distance pointe (d = 1m and 10m) of observation and excitation. The results represented graphically and illustrated by Figure 2 [(a-e) and (f-j)]. These figures represent the normalized electric fieldfor different values of conductivity 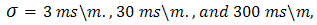 and indicate that the normalized electric field for different values of the ratio of the permittivity
and indicate that the normalized electric field for different values of the ratio of the permittivity 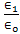 = 2, 5, 10, 30 and 100, at the distance d =1m, and 10m., respectively. The effect of the conductivity
= 2, 5, 10, 30 and 100, at the distance d =1m, and 10m., respectively. The effect of the conductivity 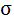 indicates that, the values of the normalized reflected electric field decrease with increasing of the conductivity
indicates that, the values of the normalized reflected electric field decrease with increasing of the conductivity  of the lower medium and the distanced. This means that with increasing distance d between the source and the receiving end, the values of the normalized reflected electric and magnetic fields decrease, furthermore, the effect of the ratio of permittivity
of the lower medium and the distanced. This means that with increasing distance d between the source and the receiving end, the values of the normalized reflected electric and magnetic fields decrease, furthermore, the effect of the ratio of permittivity 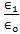 is shown in Figure 2. Figure 2[(a-c) and 2(f-h)] shows that the normalized electric field are increasing in the values with the increase of the ratio of the permittivity
is shown in Figure 2. Figure 2[(a-c) and 2(f-h)] shows that the normalized electric field are increasing in the values with the increase of the ratio of the permittivity 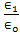 = 2, 5 and 10, at the distance d = 1m., and 10 m., respectively. Beginning with the ratio of the permittivity
= 2, 5 and 10, at the distance d = 1m., and 10 m., respectively. Beginning with the ratio of the permittivity 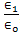 = 30, the normalized electric and magnetic fields have the fixed values as show in Figures, at the distance d = 1m, and 10m. Comparing the results in Figures 2 (d-e) and 2(i-j), we notice that for ratios of the permittivity
= 30, the normalized electric and magnetic fields have the fixed values as show in Figures, at the distance d = 1m, and 10m. Comparing the results in Figures 2 (d-e) and 2(i-j), we notice that for ratios of the permittivity 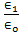 of 30 or lager, there is absolutely no effect of the reflected field on the fields observed at the distanced =1m and d =10m.
of 30 or lager, there is absolutely no effect of the reflected field on the fields observed at the distanced =1m and d =10m.9. Conclusions
- The transient electromagnetic field of an electric line source on a two-layer conducting earth can be expressed in an-analytical form, and the effect of the conductivity
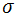 is taken into consideration.The transient electromagnetic field of an electric line source on a two-layer conducting earth has been derived in an analytical form. In these expressions, the effects of the conductivity and the ratio of permittivity have been taken into consideration. They depend on the distance between the source and the received point. It would be interesting to evaluate the normalized parallel component of the reflected electric field
is taken into consideration.The transient electromagnetic field of an electric line source on a two-layer conducting earth has been derived in an analytical form. In these expressions, the effects of the conductivity and the ratio of permittivity have been taken into consideration. They depend on the distance between the source and the received point. It would be interesting to evaluate the normalized parallel component of the reflected electric field 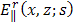 numerically with different values of the conductivity
numerically with different values of the conductivity 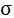 of the lower medium, and different values of the ratio of the permittivity
of the lower medium, and different values of the ratio of the permittivity 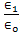 . We conclude that when the ratio of permittivity
. We conclude that when the ratio of permittivity 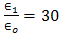 or large, there is absolutely no influence of the interfering on the received signal, even if the arrival time coincides with the free-space arrival time.
or large, there is absolutely no influence of the interfering on the received signal, even if the arrival time coincides with the free-space arrival time. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML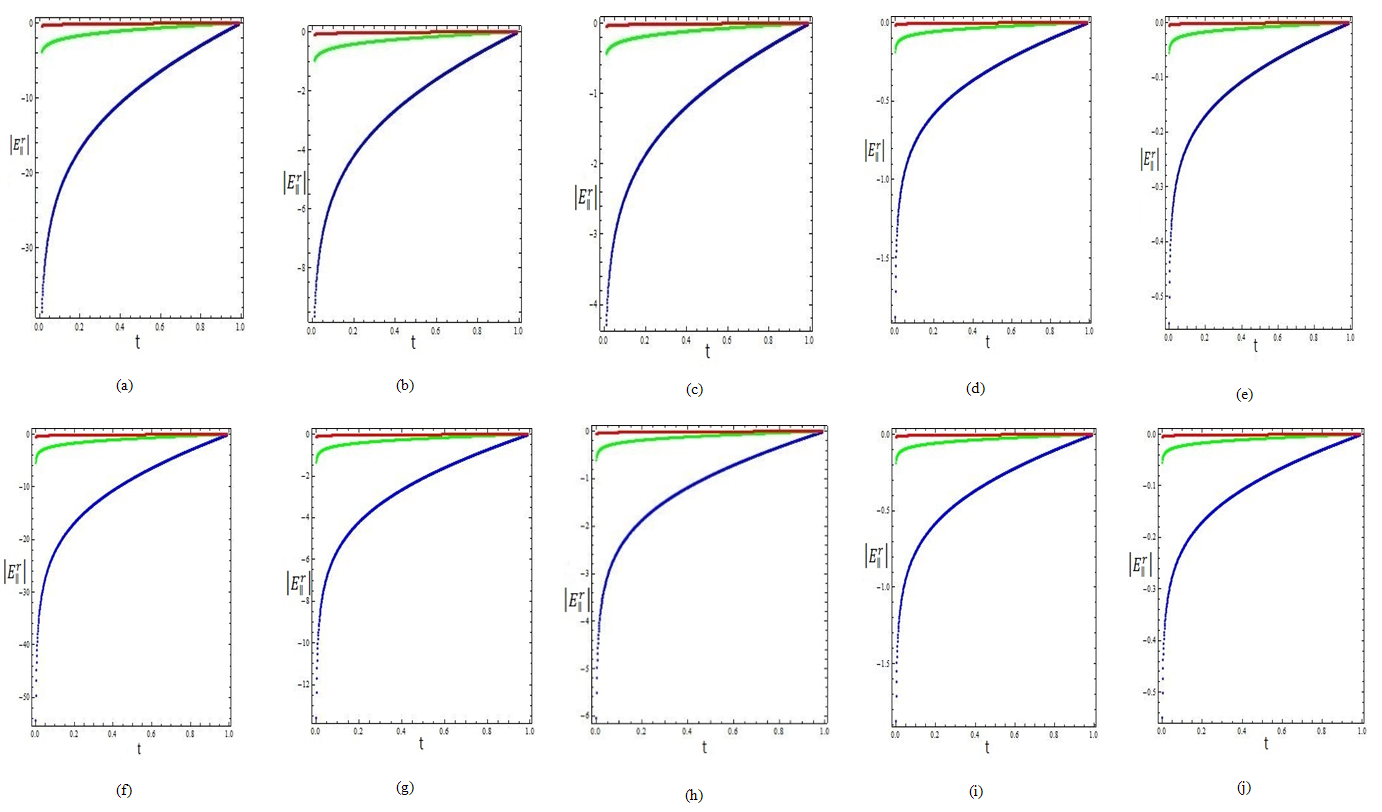
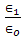 = 2,5,10, 30 and 100, respectively. Thered, green, blue curves corresponding to the values of the conductivity
= 2,5,10, 30 and 100, respectively. Thered, green, blue curves corresponding to the values of the conductivity 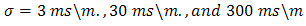 , respectively
, respectively