Usama H. Hegazy
Department of Mathematics, Faculty of Science, Al-Azhar University, Gaza, Palestine
Correspondence to: Usama H. Hegazy, Department of Mathematics, Faculty of Science, Al-Azhar University, Gaza, Palestine.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
A class of two degree of freedom nonlinear oscillators, with parametric excitation forces is considered and investigated. The case of one-to-one internal resonance and subharmonic external resonance of both modes of vibrations are considered simultaneously. Using the analytical method of multiple scales, a set of slow-flow equations governing the amplitudes and the phases of the motion is derived. Effects of system parameters on the existence and stability properties of periodic motion are studied. The frequency response curves are presented and investigation is focused on understanding the interaction of the branches of these curves as the nonlinear parameters and external forcing are varied. Finally the equations of motion are integrated numerically to verify analytical predictions. It is also found that the system exhibits different kinds of responses.
Keywords:
Resonance, Nonlinear vibration, Frequency response function
Cite this paper: Usama H. Hegazy, Internal-External Resonance and Saturation Phenomenon in a Two Coupled Nonlinear Oscillators, International Journal of Mechanics and Applications, Vol. 4 No. 3, 2014, pp. 101-114. doi: 10.5923/j.mechanics.20140403.04.
1. Introduction
The nonlinear behavior of two parametrically excited van der Pol oscillators is studied. It is found that the instabilities of quasi-periodic solutions and 3-D tori may lead to chaos as the parameters vary [1]. Parametrically excited and free vibration of weakly nonlinear oscillators under 1:3 internal resonance and two external resonances and under 1:1 internal resonance are investigated. The method of multiple time scales is applied to obtain four first order ordinary equations of the amplitudes and phases. The effect of some parameters on the stability of the system is studied using the frequency response curves. Theoretical results are verified numerically [2, 3]. Two nonlinearly coupled oscillators subjected to external periodic force are investigated. The resonant and nonresonant approximate solution is obtained using the method of multiple scales. The resonant frequency response curves and the bifurcation diagrams are studied [4]. The response of two coupled externally and parametrically excited Van der Pol oscillators to primary resonance is analyzed. Lyapunov’s first method is used to determine the stability of the proposed analytical solution obtained by the method of multiple scales perturbation technique. Effects of different parameters of the considered system on the steady-state responses are studied [5]. The free dynamics with 1:1 internal resonance of a two-dof system of nonlinear coupled oscillators are studied in the case of undamped and damped system. It is found that the undamped system admits stable and unstable synchronous motion in the neighborhood of the resonance case and a bifurcation diagram is constructed. When damping is considered, it is shown that sustained resonance captured appears to provide a dynamical mechanism for passively transferring energy from one art of the system to another, which is directly related to the essential stiffness nonlinearity of the system [6]. The slow flow equations governing the modulation of the amplitudes and the phases of two nonlinearly coupled van der Pol oscillators to parametric excitation in the presence of one-to-one internal resonance are derived. Energy considerations are used to investigate the existence and characteristics of limit cycles of the slow flow equations [7]. Periodic and homoclinic motions in periodically forced, weakly coupled oscillators is studied. Different types of homoclinic motions occur in the considered system and the relationship between the subharmonic and homoclinic Melnikov theories is discussed [8]. The multiple scales perturbation theory is used to obtain approximate periodic solutions of a two coupled Duffing-van der Pol oscillators, which is investigated analytically and numerically. The effects of different parameters on the system response is studied and analytical predictions are confirmed numerically. It is shown that bifurcation leading to quasiperiodic attractor and jump phenomenon occur in the system [9]. A bifurcation analysis in a damped Mathieu and a damped harmonic oscillators to parametric excitations is studied analytically and numerically. Complex periodic windows in the chaotic regions are discovered, which allow the control of chaos. It is shown that the stable solutions lose their stability by either period doubling or intermittency when the parameters leave their shrimps in different directions [10]. The periodic and chaotic responses of a rotor-AMB system with quadratic and cubic nonlinearities and time-varying stiffness are investigated considering the simultaneous primary resonance case. Using the method of multiple scales, the frequency response equation is obtained and solved numerically to obtain the steady-state solution, and the stability is determined by the eigenvalues of the corresponding Jacobian matrix. Rung-Kutta fourth order ethod is applied to explore the non-linear chaotic and resonant behavior of the system [11]. The principal parametric resonance is studied in the parametrically excited two-degree-of-freedom AMB system with time-varying stiffness. Different effects of the system parameters are investigated. The theoretical results obtained by the method of multiple scale are verified by numerically [12]. The effect of the parametric excitations on the nonlinear response and chaotic motion of the string-beam coupled system under the case of one-to-two internal resonance between the modes of the string and the beam, in the presence of subharmonic resonances. Numerical simulations illustrated that multiple-valued solutions, jump phenomenon, hardening and softening nonlinearities occur in the resonant frequency response curves [13].In this paper, the nonlinear oscillations and chaotic dynamics of a coupled nonlinear system under parametric excitation are investigated. The method of multiple scales is utilized to obtain the frequency response equations, which are numerically solved to obtain the steady-state responses. The analysis of stability for model is also given. The behavior of the system is studied applying Rung-Kutta fourth order method. The numerical solution of both modes of vibration is obtained at non-resonant case, simultaneous internal and principal parametric resonance. The effect of different parameters on the system behavior and its stability are also investigated. The results obtained show that the chaotic motion can occur in a parametrically excited nonlinear coupled oscillators. The numerical simulations verify the analytical predictions.
2. Perturbation Analysis
The equations of motion governing the model in non-dimensional form [2], have been modified as follows: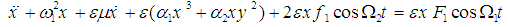 | (1) |
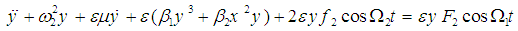 | (2) |
where ω1,2 are two linear natural frequencies, μ is the damping coefficient, f1,2 and F1,2 are the amplitudes of the forcing excitations, αi, βi (i = 1,2) are the coefficients of nonlinear terms, ε is a small dimensionless parameter, and Ω1,2 are the frequencies of the excitation. More details about Eqs. (1), (2) and their parameters are given in Appendix A. To determine a first-order uniform expansion for Eqs. (1) and (2) when ω1 = ω2 and Ω1 = 2ω1 = 2ω2, one uses the method of multiple scales. We seek a first-order uniform expansion of the solution of Eqs. (1) and (2) in the form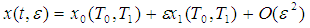 | (3) |
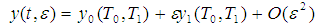 | (4) |
where, 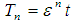 , T0 is the fast time scale associated with changes occurring at the frequencies ω1,2 and Ω1,2 and T1 is the slow time scale associated with modulations in the amplitudes and phases caused by the nonlinearity, damping, and resonances.In terms of T0 and T1, the time derivatives become:
, T0 is the fast time scale associated with changes occurring at the frequencies ω1,2 and Ω1,2 and T1 is the slow time scale associated with modulations in the amplitudes and phases caused by the nonlinearity, damping, and resonances.In terms of T0 and T1, the time derivatives become: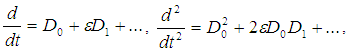 | (5) |
where 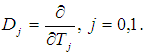 Substituting for
Substituting for  and
and 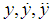 in Eq. (1) and (2), and equating the coefficients of the same powers of ε we obtain the following differential equations
in Eq. (1) and (2), and equating the coefficients of the same powers of ε we obtain the following differential equations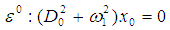 | (6) |
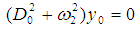 | (7) |
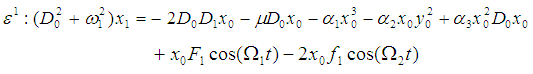 | (8) |
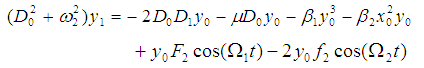 | (9) |
The general solution of Eqs. (6) and (7) can be written as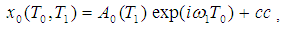 | (10) |
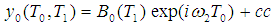 | (11) |
where A0, B0 are complex functions in T1, which are defined in the next section (cc denotes a complex conjugate of the preceding term). Substituting Eqs. (10), (11) into Eqs. (8), (9), we get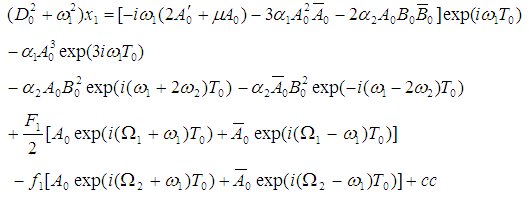 | (12) |
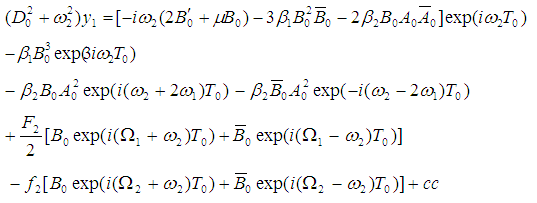 | (13) |
where the prime indicates the derivative with respect to T1. Any particular solutions of equations (12) and (13) contain secular terms proportional to exp(± iω1,2T0), and it contains small-divisor terms if the following resonant conditions are satisfied simultaneously: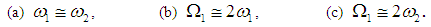 The first resonance is called internal resonance or auto-primary resonance, and the last two resonances are called principal parametric resonances. In this paper, we analyze the case
The first resonance is called internal resonance or auto-primary resonance, and the last two resonances are called principal parametric resonances. In this paper, we analyze the case 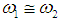 in the presence of
in the presence of 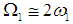 and
and 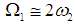 , which has been confirmed numerically.
, which has been confirmed numerically.
3. Simultaneous Resonance of the System
The closeness of the resonances is described by introducing the external detuning parameters σ1, σ2, and σ3 as 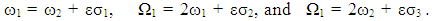 | (14) |
Using (14) in eliminating terms that produce secular terms from Eqs. (12) and (13) gives the solvability conditions as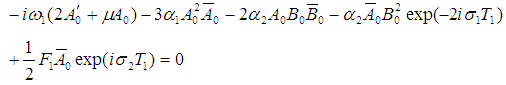 | (15) |
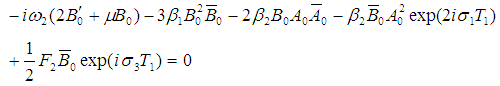 | (16) |
Substituting the polar forms  | (17) |
into Eqs. (15) and (16), where a1,2 and θ1,2 are the steady-state amplitudes and the phases of the motions respectively, then separating the real and imaginary parts gives governing equations of the amplitudes аi and phases γi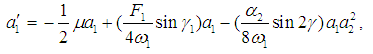 | (18) |
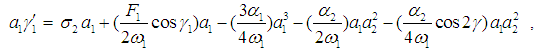 | (19) |
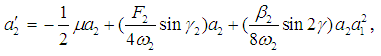 | (20) |
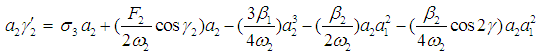 | (21) |
where θ = θ2 – θ1, γ1 = σ2 T1 – 2θ1, γ2 = σ3 T1 – 2θ2, and γ = θ – σ1T1. The steady-state solutions correspond to constant solutions, that is correspond to 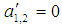 and
and 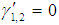 . Hence the fixed points of Eqs. (18)-(21) are given by
. Hence the fixed points of Eqs. (18)-(21) are given by 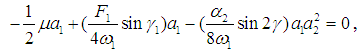 | (22) |
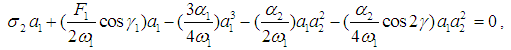 | (23) |
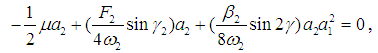 | (24) |
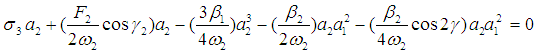 | (25) |
From Eqs. (22)-(25), we have the following possible solutions besides the trivial solution:Single-mode (unimodal) solutions:Case 1: a1 = 0 and a2 ≠ 0. Squaring Eqs. (24) and (25), then adding the squared results together gives the following frequency response equation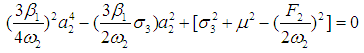 | (26) |
Case 2: a1 ≠ 0 and a2 = 0. Squaring Eqs. (22) and (23), then adding the squared results together gives the following frequency response equation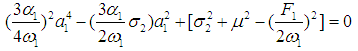 | (27) |
Two-mode (bimodal) solutions: Case 3: a1 ≠ 0 and a2 ≠ 0. Squaring Eqs. (22) and (23), then adding the squared results together, similarly to Eqs. (24) and (25) gives the following frequency response equations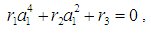 | (28) |
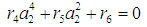 | (29) |
where ri ( i = 1,2,…6) are defined in Appendix B.To study the stability of the fixed point solutions of Eqs. (18)-(21), we introduce the following forms 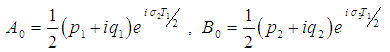 | (30) |
where p1,2, q1,2 are real. Substitution the above forms of A0, and B0 into the linearized form of Eqs. (15), (16), that is into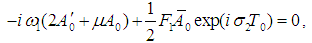 | (31) |
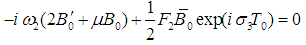 | (32) |
Then separating real and imaginary parts, gives the following equations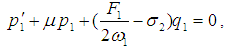 | (33) |
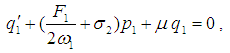 | (34) |
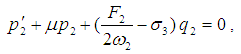 | (35) |
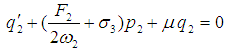 | (36) |
To determine the stability of the fixed points, we evaluate the Jacobian matrix of (33)-(36), then the zeros of the characteristic equation (the eigen equation) is given by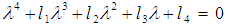 | (37) |
where li, i=1,2,3,4 are constants, given in Appendix B. The Routh-Hurwitz criterion guarantees that all eigenvalues have negative real parts, and hence the fixed points are asymptotically stable, if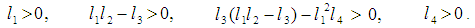
4. Frequency Response Curves
The periodic solutions corresponding to the fixed points of Eqs. (18)-(21) for simultaneous internal and principle parametric resonances of the two modes are obtained when 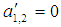 and
and 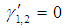 . From the resulting equations, the frequency response equations (26)-(29) are obtained and solved numerically. The numerical results are presented Figs. (1)-(4) as the amplitudes a1,2 against the detuning parameters σ3,2 for different values of other parameters. The stable solutions are represented by solid lines and the unstable solutions are represented by the dotted lines.
. From the resulting equations, the frequency response equations (26)-(29) are obtained and solved numerically. The numerical results are presented Figs. (1)-(4) as the amplitudes a1,2 against the detuning parameters σ3,2 for different values of other parameters. The stable solutions are represented by solid lines and the unstable solutions are represented by the dotted lines.
4.1. Response Curves of Case 1 and 2
Considering Fig. (1a) as basic case for comparison, it can be seen from Figs. (1b) and (1c) that as the forcing excitation amplitude F2 decreases and the natural frequency ω2 increases, the branches of the response curves converge to each other, the region of unstable solutions and the amplitude decrease. The response curves in Fig. (1d) are not significantly affected as the damping coefficient µ increases, while the amplitude decreases. Figs. (1e) and (1f) show several representative curves for the variation of steady-state amplitude as the nonlinear term β1 is varied. Comparing these curves shows that the nonlinearity effect bends the frequency response curves to left (softening nonlinearity) when β1 is positive and to right (hardening nonlinearity) when β1 is negative. This leads to a multi-valued solutions and hence to jump phenomenon occurrence. For the second case, the steady-state amplitude a1 is plotted against the detuning parameter σ1, as shown in Figs. (2a)-(2f). These figures illustrate similar effects of parameters, that was reported in case 1. 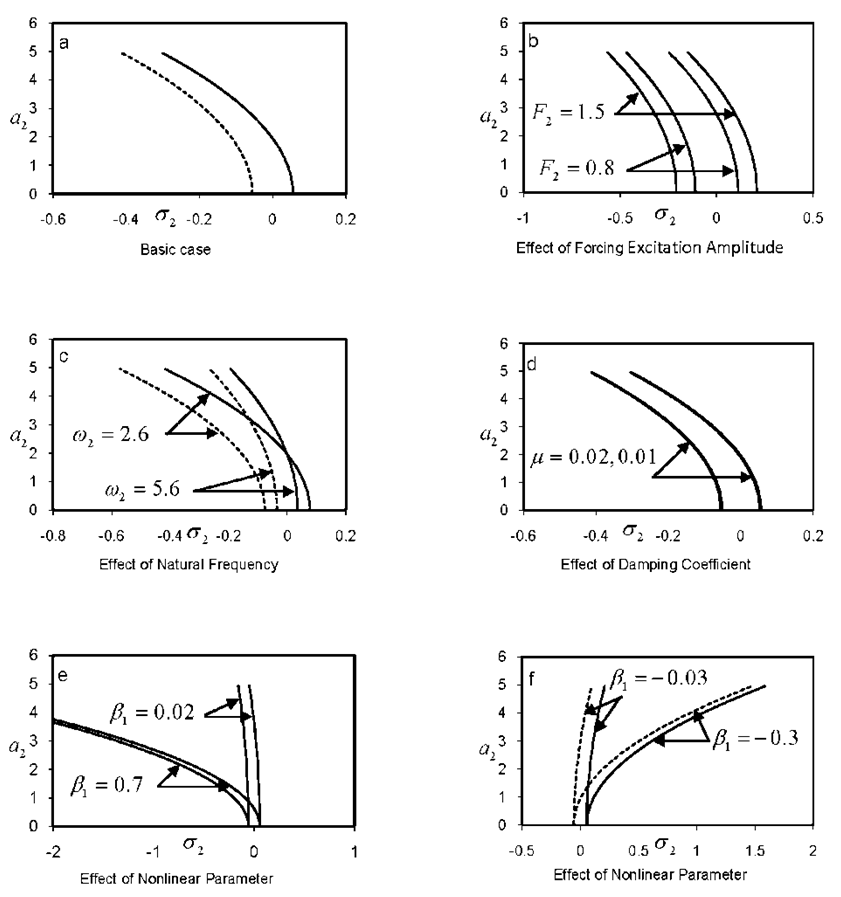 | Figure 1. Response curves of case 1: a1 = 0, a2 ≠ 0, F2 = 0.4, ω2=3.6, μ = 0.0003, β1 = 0.07 |
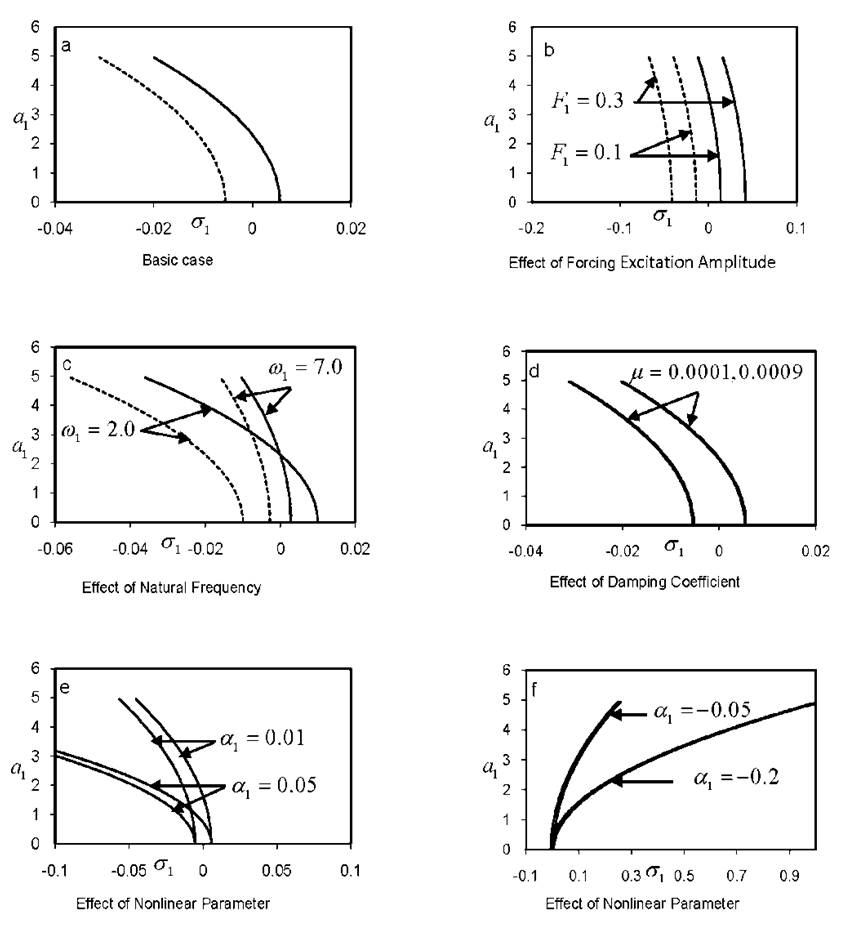 | Figure 2. Response curves of case 2: a1 ≠ 0, a2 = 0, F1 = 0.04, ω1=3.6, μ = 0.0003, α1 = 0.005 |
4.2. Response Curves of Case 3
The frequency response curves for both modes in Figs. (3) and (4) show a hardening nonlinearity except for those in Figs. (3e) and (4e), where the curves are bent to the right indicating a softening behavior. The nonlinear coefficients α2 and β2 have trivial effect on the frequency response curves as shown in Figs (3g) and (4g), respectively.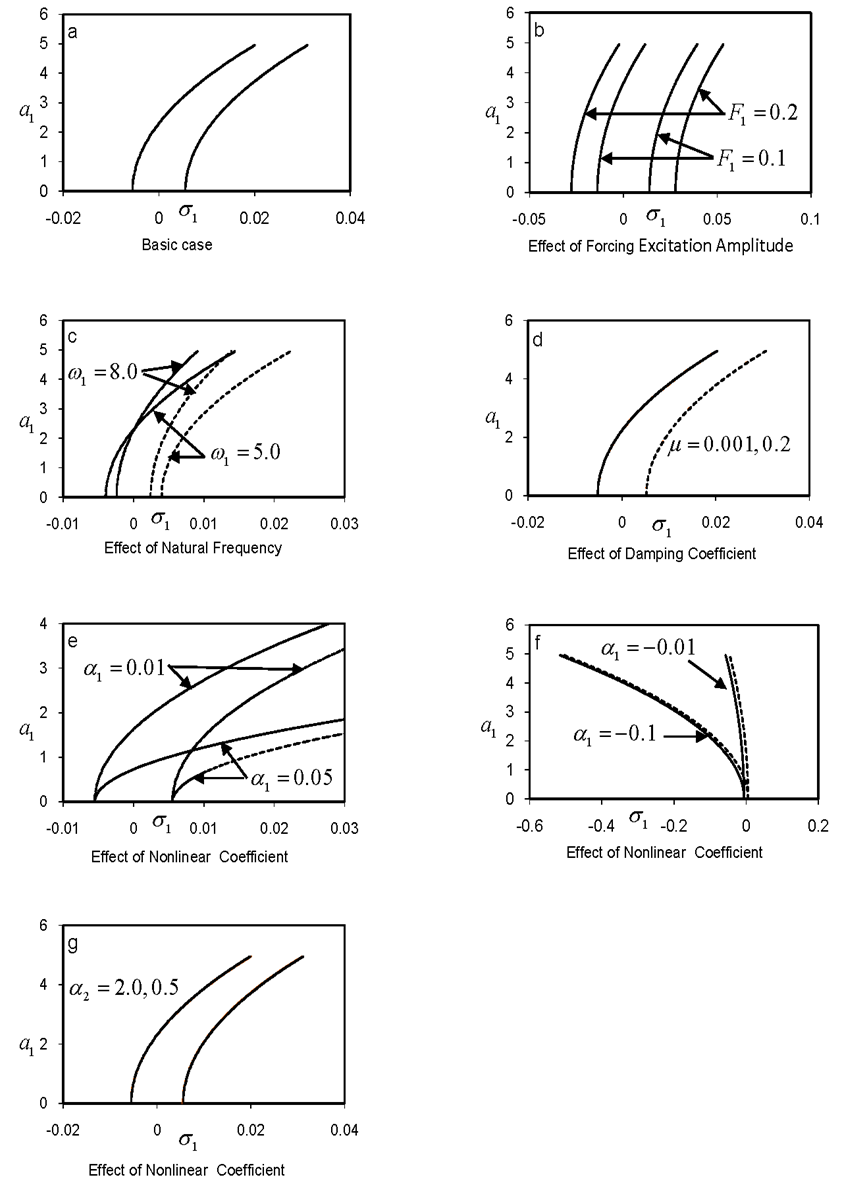 | Figure 3. Response curves of case 3: a1 ≠ 0, a2 ≠ 0, F1 = 0.04, ω1=3.6, μ = 0.0003, α1 = 0.005, α2 = 0.02 |
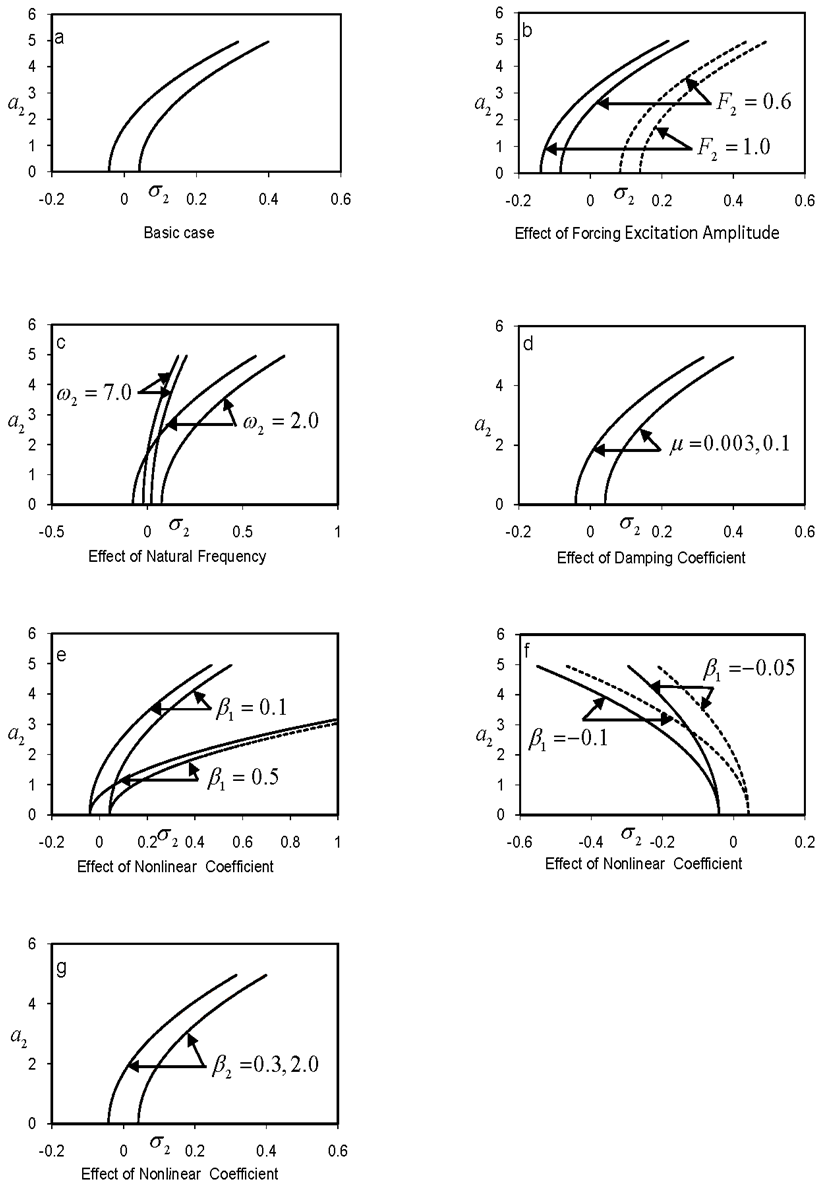 | Figure 4. Response curves of case 3: a1 ≠ 0, a2 ≠ 0, F2 = 0.3, ω2=3.6, μ = 0.0003, β1 = 0.07, β2 = 0.02 |
5. Numerical Solution
Numerical integration to Eqs. (1) and (2) are carried out using a fourth order Runge-Kutta algorithm to verify analytic predictions. A non-resonant system behavior for both modes is shown in Fig. (5). The behavior of the system under simultaneous internal and principal parametric resonant conditions, Fig. (6), illustrates that the steady-state amplitude in the horizontal and vertical direction is increased to about 900% and 1125%, respectively.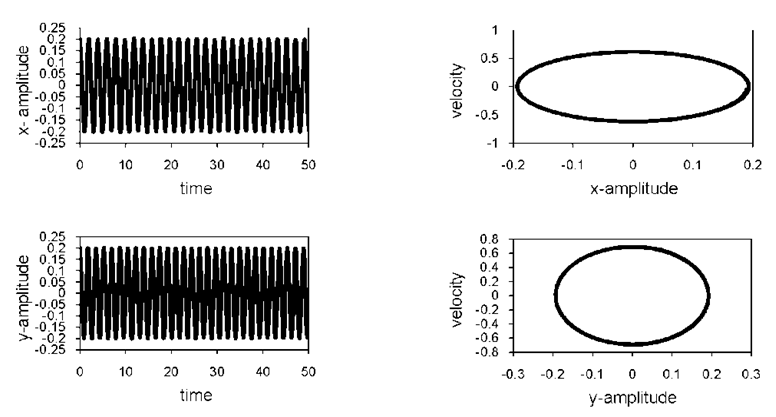 | Figure 5. Non-resonant time response solution: F1 = 0.4, f1 = 0.2, F2 = 0.3, f2 = 0.1; Ω1 = 2.2, Ω2 = 1.9, ω1=3.2, ω2=3.6, μ = 0.0003, α1 = 0.005, α2 = 0.02, β1 = 0.07, β2 = 0.02 |
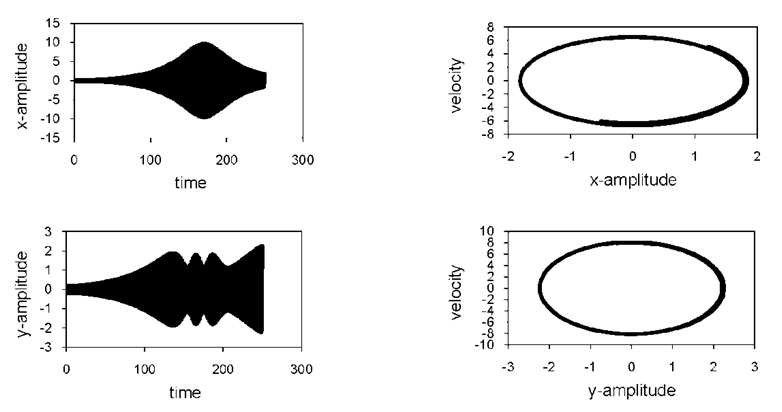 | Figure 6. Simultaneous internal and principal parametric resonance solution |
5.1. Effect of the Amplitude of the Forcing Excitations f1,2
Figs. (7a) and (7b). illustrates that x- and y-amplitudes are monotonic increasing functions in the forcing excitation amplitudes f1,2, respectively.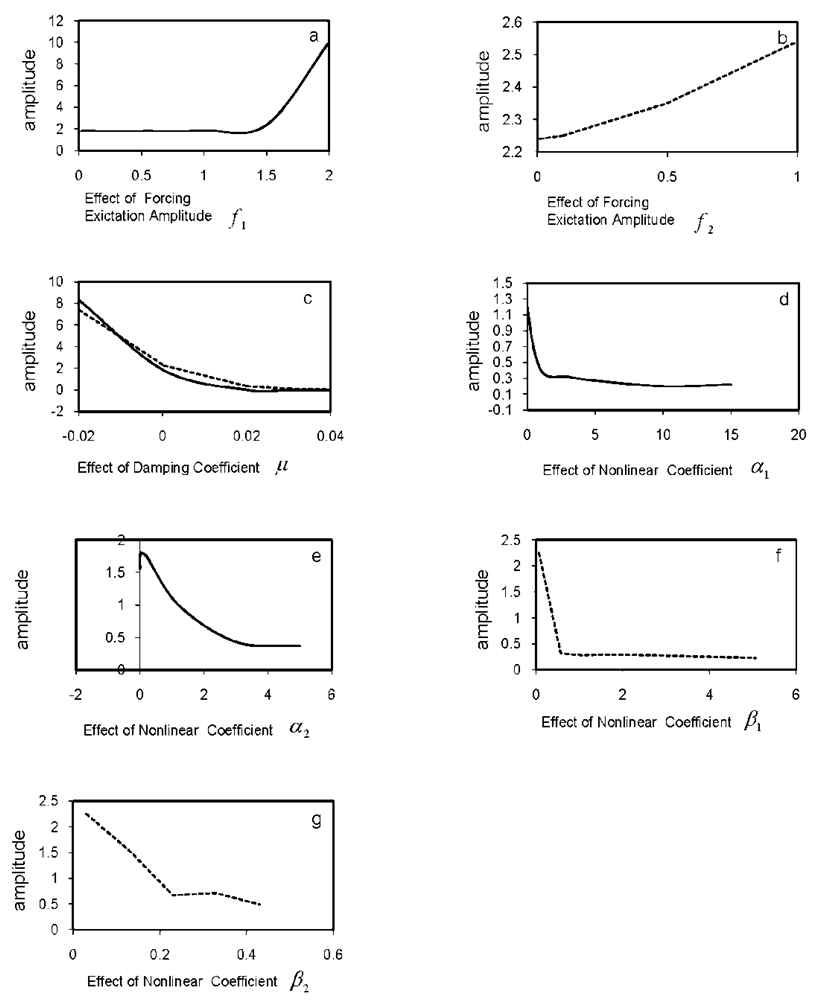 | Figure 7. Numerical solution under various values of the parameters at simultaneous internal and principal parametric resonance conditions; (dashed line is the x- amplitude, solid line is the y- amplitude) |
5.2. Effect of Damping Coefficient
It can be seen from Fig. (7c), that for negative values of the damping coefficient µ, the amplitude of both modes of vibration increases, which may lead to unstable system. Whereas, for positive values of µ, the amplitudes of x and y are monotonic decreasing functions. This parameter can be used to control the system amplitude, where more increase of µ leads to saturation phenomena.
5.3. Effect of Nonlinear Coefficients
Figs. (7d)-(7g) show the effect of different nonlinear coefficients α1,2 and β1,2 on the x- and y- amplitudes, where a saturation phenomena is noticed as magnitude of the nonlinear coefficients increases. The x- and y- amplitudes are monotonic decreasing functions in the nonlinear terms α1,2 and β1,2, respectively. Both effects of parameters in the frequency response results, Figs. (1)-(4), and the numerical solution results, Fig. (7), are in a good agreement.
5.4. Effect of the Amplitude of the Forcing Excitations F1,2
The effects of the amplitude of the forcing excitations F1 and F2 are shown in Figs. (8,9), which represent the time-series solution (t, x), (t, y) for the horizontal and vertical modes respectively at resonant case. Considering Fig. (6) as basic case for comparison. It can be seen from Fig. (8) that as the amplitude of the forcing excitation F1 increases, a chaotic motion occurs for the horizontal and vertical modes. The time trace in Fig. (8b) indicates that the response of the first and second mode is periodically and chaotically modulated, respectively. As F1 increases further, the amplitude of the modulated response of both modes increases considerably, causing the shape of the chaotic motion to change. Similar behavior for the chaotic motion is shown in Fig. (9) as the amplitude of the forcing excitation F2 changes.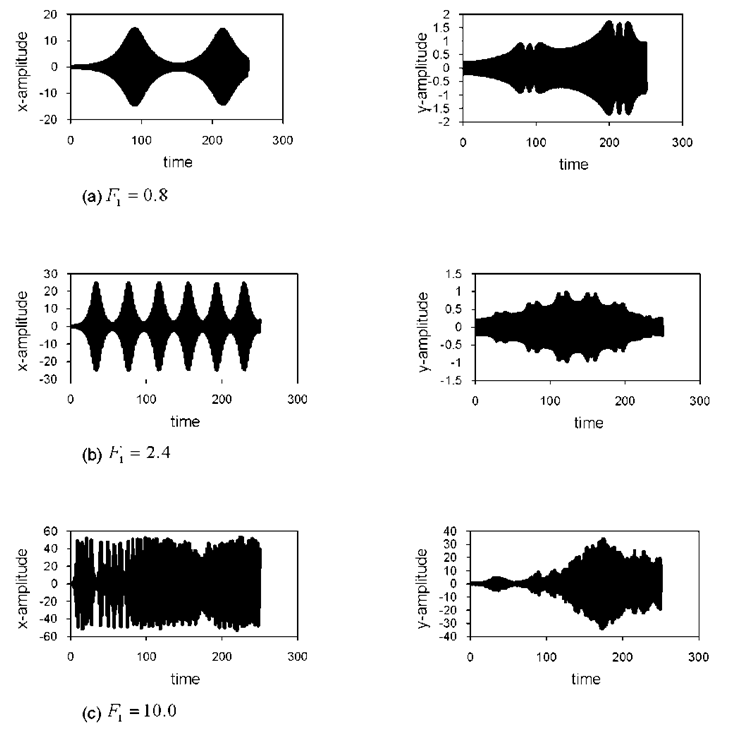 | Figure 8. Effect of external forcing excitation amplitude F1 at simultaneous internal and principal parametric resonance conditions |
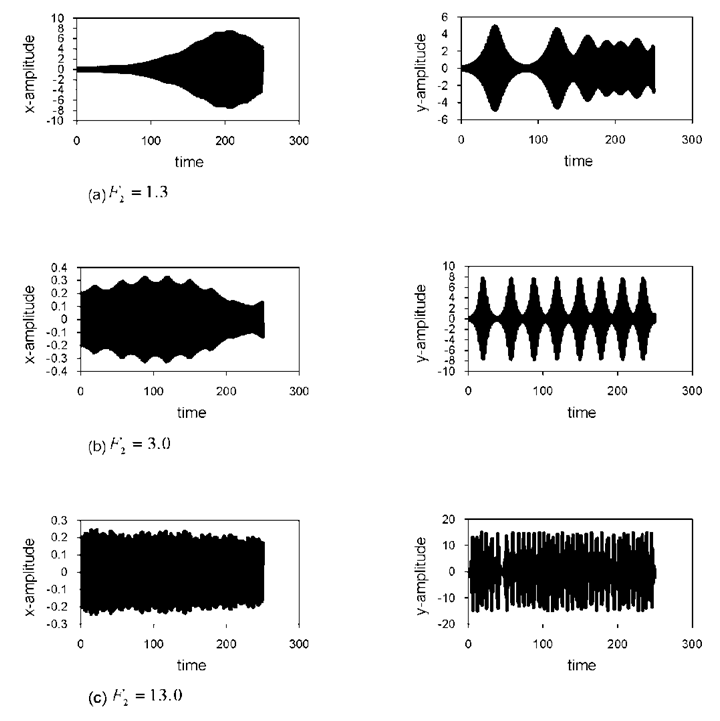 | Figure 9. Effect of external forcing excitation amplitude F2 at simultaneous internal and principal parametric resonance conditions |
6. Conclusions
The nonlinear response ad chaotic motion of a two degree of freedom nonlinear system non under both external and internal excitations are investigated, where internal as well as external resonance conditions have been considered. The method of multiple scales is applied to determine the simultaneous resonance case and to study the system stability. The stability of the system and the effects of different parameters on system behavior have been studied under the considered resonance cases applying the frequency response equation method. They have been confirmed numerically. The numerical results are focused on both the effects of different parameters and the response of the system. The shape of the chaotic motions in the horizontal and vertical directions is also investigated. It may be concluded that:1. The considered model has a variety of interesting phenomenon such as multi-valued solutions, jump, softening and hardening nonlinearities. 2. The steady-state amplitudes of both modes are monotonic increasing functions in the internal forcing excitation amplitudes f1,2. More increase may lead to unstable behavior. 3. The steady-state amplitudes are monotonic decreasing functions in the damping coefficient μ, and the nonlinear parameters α1,2, β1,2. Further increase may lead to saturation phenomena.4. For the external forcing excitation amplitudes F1,2, as the magnitude of any excitation amplitude is increased, a chaotic motion occurs in the horizontal and vertical directions. When the amplitudes F1,2 change, the chaotic behavior changes leading to the appearance of periodically and chaotically modulated oscillations in the system.
Appendix A
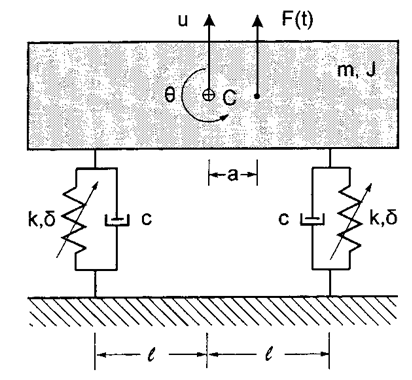 | Figure 1A. The model of a mechanical system, [2] |
The derivation of non-dimensional formulation is similar to that obtained in [2]. The system under investigation, shown in Fig. 1A, consists of a rigid machine with two identical supports and has mass m and moment of inertia J. The form of the restoring force developed in each support due to a displacement u(t) is given by 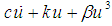 , where c and k are linear viscous damping and the Duffing-type stiffness of the two supports, respectively. In our work, the stiffness is assumed to have the periodic form
, where c and k are linear viscous damping and the Duffing-type stiffness of the two supports, respectively. In our work, the stiffness is assumed to have the periodic form 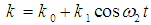 , where Ω2 is the frequency of varying stiffness and the response of the system will be studied under parametric excitation. The rigid machine can translate in the vertical direction x by u and also rotate in a vertical plane by θ. Applying normalization, one obtains the equations of motion of the system in the forms (1) and (2).
, where Ω2 is the frequency of varying stiffness and the response of the system will be studied under parametric excitation. The rigid machine can translate in the vertical direction x by u and also rotate in a vertical plane by θ. Applying normalization, one obtains the equations of motion of the system in the forms (1) and (2).
Appendix B
Coefficients of Eqs. (28) and (29)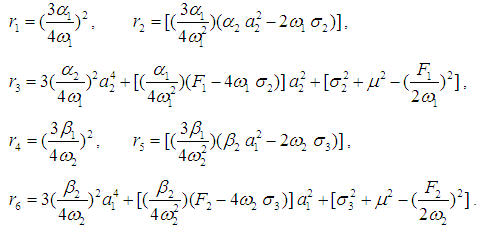 Coefficients of Eq. (37)
Coefficients of Eq. (37)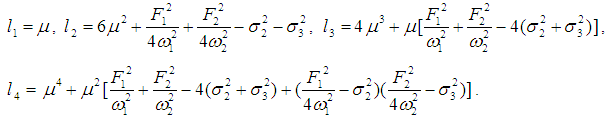
References
| [1] | Q. Bi, Dynamical analysis of two coupled parametrically excited van der Pol oscillators, Inter. J. of Non-linear Mech., 2004, 39, 33-54. |
| [2] | S. Mitis, S. Natsiavas, and I. Tsiafis, Dynamics of nonlinear oscillators under simultaneous internal and external resonances, Nonlinear Dyn, 1998, 16, 23-39. |
| [3] | S. Natsiavas, Free vibration of two coupled nonlinear oscillator, Nonlinear Dyn, 1994, 6, 69-86. |
| [4] | P. Woafo, H. B. Fotsin and J. C. Chedjou, Dynamics of two nonlinearly coupled oscillators” Physica Scripta, 1998, 57, 195-200. |
| [5] | M. M. Kamel, Nonlinear behavior of Van der Pol oscillator under parametric and harmonic excitations, Physica Scripta, 2009, 79, 025004 (8 pages). |
| [6] | A. F. Vakakis and R. J. Rand, Non-linear dynamics of a system of coupled oscillators with essential stiffness non-linearities, Inter. J. of Non-linear Mech. 2004, 39, 1079-1091. |
| [7] | A. Maccari, Parametric excitation for two internally resonant van der Pol oscillators, Nonlinear Dyn., 2002, 27, 367-383. |
| [8] | K. Yagasaki, Periodic and harmonic motions in forced, coupled oscillators, Nonlinear Dyn., 1999, 20, 319-359. |
| [9] | S. Rajasekar and K, Murali, Resonance behavior and jump phenomenon in a two coupled Duffing-van der Pol oscillators, Chao, Solitons and Fractals, 2004, 19, 925-934. |
| [10] | Y. Zou, M. Thiel, M.C Romanto and J. Kurths, Shrimp structure and associated dynamics in parametrically excited oscillators, Inter. J. of Bifurcation and Chaos, 2006, 12, 3567-3579. |
| [11] | Y. A. Amer and U. H. Hegazy, Resonance behaviour of a rotor-active magnetic bearing with time-varying stiffness. Chaos Solitons Fractals, 2007, 34, 1328–1345. |
| [12] | U. H. Hegazy and Y. A. Amer, A time-varying stiffness rotor-active magnetic bearings under parametric excitation. Proceeding of the Institution of Mechanical Engineers Part C: J. Mech. Eng. Sci, 2008, 222(3), 447–458. |
| [13] | Y. A. Amer and U. H. Hegazy, Chaotic Vibration and Resonance Phenomena in a Parametrically Excited String-Beam Coupled System. Meccanica, 2012, 47(4), 969–984. |



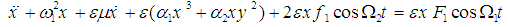
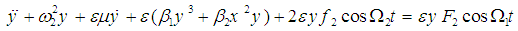
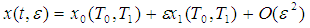
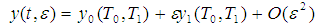
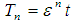 , T0 is the fast time scale associated with changes occurring at the frequencies ω1,2 and Ω1,2 and T1 is the slow time scale associated with modulations in the amplitudes and phases caused by the nonlinearity, damping, and resonances.In terms of T0 and T1, the time derivatives become:
, T0 is the fast time scale associated with changes occurring at the frequencies ω1,2 and Ω1,2 and T1 is the slow time scale associated with modulations in the amplitudes and phases caused by the nonlinearity, damping, and resonances.In terms of T0 and T1, the time derivatives become: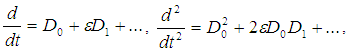
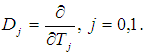 Substituting for
Substituting for 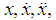 and
and 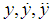 in Eq. (1) and (2), and equating the coefficients of the same powers of ε we obtain the following differential equations
in Eq. (1) and (2), and equating the coefficients of the same powers of ε we obtain the following differential equations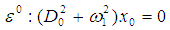
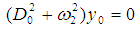
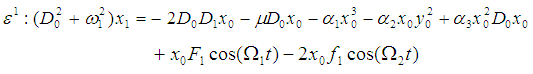
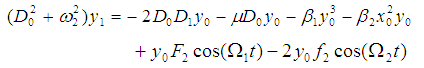
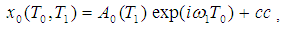
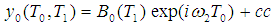
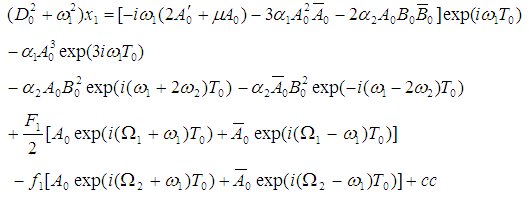
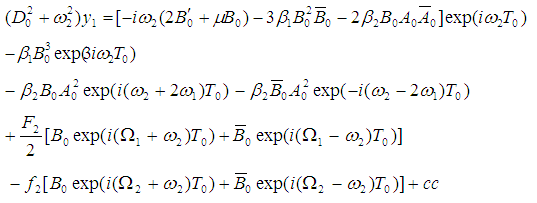
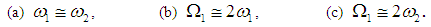 The first resonance is called internal resonance or auto-primary resonance, and the last two resonances are called principal parametric resonances. In this paper, we analyze the case
The first resonance is called internal resonance or auto-primary resonance, and the last two resonances are called principal parametric resonances. In this paper, we analyze the case 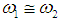 in the presence of
in the presence of 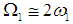 and
and 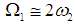 , which has been confirmed numerically.
, which has been confirmed numerically.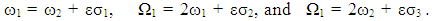
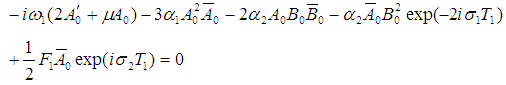
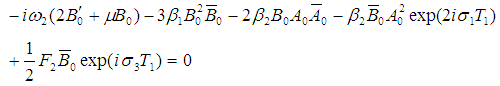

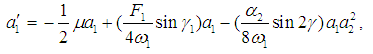
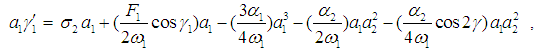
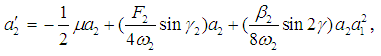
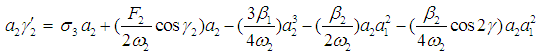
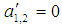 and
and 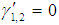 . Hence the fixed points of Eqs. (18)-(21) are given by
. Hence the fixed points of Eqs. (18)-(21) are given by 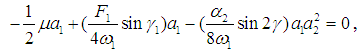
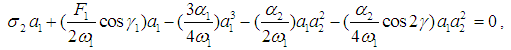
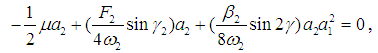
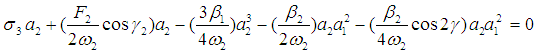
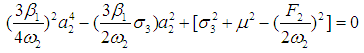
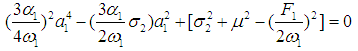
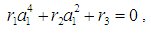
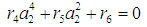
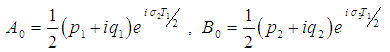
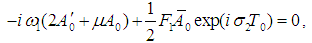
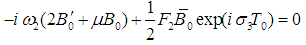
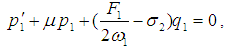
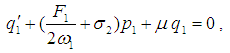
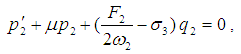
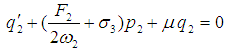
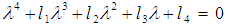
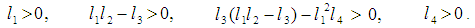
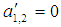 and
and 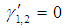 . From the resulting equations, the frequency response equations (26)-(29) are obtained and solved numerically. The numerical results are presented Figs. (1)-(4) as the amplitudes a1,2 against the detuning parameters σ3,2 for different values of other parameters. The stable solutions are represented by solid lines and the unstable solutions are represented by the dotted lines.
. From the resulting equations, the frequency response equations (26)-(29) are obtained and solved numerically. The numerical results are presented Figs. (1)-(4) as the amplitudes a1,2 against the detuning parameters σ3,2 for different values of other parameters. The stable solutions are represented by solid lines and the unstable solutions are represented by the dotted lines. 








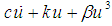 , where c and k are linear viscous damping and the Duffing-type stiffness of the two supports, respectively. In our work, the stiffness is assumed to have the periodic form
, where c and k are linear viscous damping and the Duffing-type stiffness of the two supports, respectively. In our work, the stiffness is assumed to have the periodic form 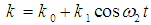 , where Ω2 is the frequency of varying stiffness and the response of the system will be studied under parametric excitation. The rigid machine can translate in the vertical direction x by u and also rotate in a vertical plane by θ. Applying normalization, one obtains the equations of motion of the system in the forms (1) and (2).
, where Ω2 is the frequency of varying stiffness and the response of the system will be studied under parametric excitation. The rigid machine can translate in the vertical direction x by u and also rotate in a vertical plane by θ. Applying normalization, one obtains the equations of motion of the system in the forms (1) and (2).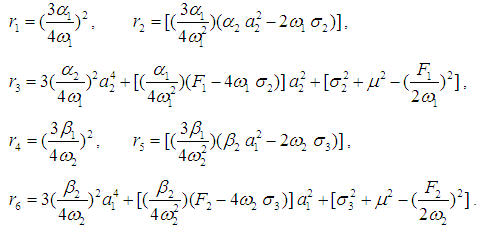 Coefficients of Eq. (37)
Coefficients of Eq. (37)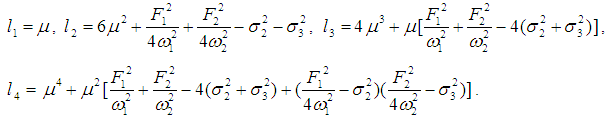
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML