-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Mechanics and Applications
p-ISSN: 2165-9281 e-ISSN: 2165-9303
2014; 4(3): 94-100
doi:10.5923/j.mechanics.20140403.03
Free Vibration Analysis of Beams Considering Different Geometric Characteristics and Boundary Conditions
Mehmet Avcar
Civil Engineering Department, Engineering Faculty, Suleyman Demirel University, Isparta, Turkey
Correspondence to: Mehmet Avcar, Civil Engineering Department, Engineering Faculty, Suleyman Demirel University, Isparta, Turkey.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
In this study, free vibration of square cross-sectioned aluminum beams is investigated analytically and numerically under four different boundary conditions: Clamped-Clamped (C-C), Clamped-Free (C-F), Clamped-Simply Supported (C-SS) and Simply Supported-Simply Supported (SS-SS). Analytical solution is carried out using Euler-Bernoulli beam theory and Newton Raphson Method. First, the equations of motion are provided. Then, solutions including the effects of the geometric characteristics, and boundary conditions are obtained and discussed for the natural frequencies of the first three modes. To confirm the reliability of the vibration analysis carried out in the present paper as well, all the analytical results are checked with the corresponding numerical results obtained from the finite-element-method (FEM) based software called ANSYS. Numerical and analytical results are found to be good agreement.
Keywords: Free Vibration, Beam, Natural Frequency, Boundary Conditions, Geometric Characteristics
Cite this paper: Mehmet Avcar, Free Vibration Analysis of Beams Considering Different Geometric Characteristics and Boundary Conditions, International Journal of Mechanics and Applications, Vol. 4 No. 3, 2014, pp. 94-100. doi: 10.5923/j.mechanics.20140403.03.
Article Outline
1. Introduction
- A beam is a slender horizontal structural member that resists lateral loads by bending, and this important element of engineering structures appears in various forms and comprises various artifacts, such as supporting members in high-rise buildings, railways, long-span bridges, flexible satellites, gun barrels, robot arms, airplane wings, etc. [1, 2]. In many engineering applications, beams are subjected to dynamic loads, which can excite beam structural vibrations and cause durability concerns or discomfort because of the resulting noise and vibration. In addition, if the vibration exceeds certain limits, there is the danger of beam breakage or failure [3-6]. Due to beams are important structural elements, vibration analysis has been a vital task in their design for engineers and researchers for more than a century. Early investigations of the theory of vibration were given in Refs [7-9]. Then an increasing interest has been observed regarding the vibration of beams, and several studies have appeared in the general literature, some of which are provided in the Refs [10-25].In this study, the free vibration of square cross-sectioned aluminum beams is investigated analytically and numerically under four different boundary conditions. Analytical solution is carried out using Euler-Bernoulli beam theory, in which material is assumed to be linear-isotropic, and Newton Raphson Method. This method is based on the simple idea of linear approximation, and used for finding the roots of equations. It is particularly useful for transcendental equations, composed of mixed trigonometric and hyperbolic terms. Such equations occur in vibration analysis. An example is the calculation of natural frequencies of continuous structures [26]. Solutions including the effects of the geometric characteristics, i.e., length and cross sectional area, and boundary conditions are obtained and discussed for the natural frequencies of the first three modes. Furthermore, to confirm the reliability of the vibration analysis carried out in the present paper as well, all the analytical results are checked with the corresponding numerical results obtained from Finite Element Method (FEM)-based software called ANSYS [27], where the method is established on the idea of building a complicated object with simple blocks, or, dividing a complicated object into smaller and manageable pieces [28]. Present analysis can be used as a comparative study or data for the different solution methods of future works in the related field.
2. Basic Equations
- Consider an elastic beam of length
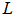 , Young's modulus
, Young's modulus 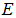 , and mass density
, and mass density 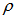 with uniform cross section
with uniform cross section 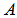 , as shown in Figure 1.
, as shown in Figure 1. 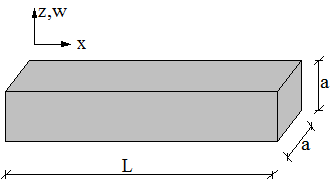 | Figure 1. Geometry of the beam |
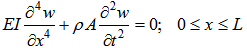 | (1) |
 is the area moment of inertia of the beam cross section,
is the area moment of inertia of the beam cross section,  is the transverse displacement, and t is time. Eq. (1) can be rearranged as follows:
is the transverse displacement, and t is time. Eq. (1) can be rearranged as follows: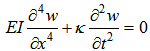 | (2) |
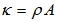 is the linear mass density of the beam. The solution of the Eq. (2) is sought by separation of variables. Assume that the displacement can be separated into two parts: one is depending on the position and the other is depending on time, as follows:
is the linear mass density of the beam. The solution of the Eq. (2) is sought by separation of variables. Assume that the displacement can be separated into two parts: one is depending on the position and the other is depending on time, as follows: 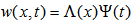 | (3) |
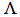 and
and 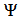 are independent of time and position, respectively.Substituting Eq. (3) into Eq. (2) and after some mathematical rearrangements, the following equation is obtained:
are independent of time and position, respectively.Substituting Eq. (3) into Eq. (2) and after some mathematical rearrangements, the following equation is obtained: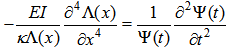 | (4) |
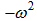 to have simple harmonic motion in the system.
to have simple harmonic motion in the system. 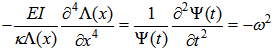 | (5) |
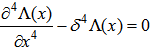 | (6) |
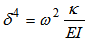 | (7) |
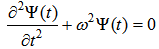 | (8) |
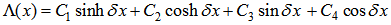 | (9) |
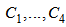 are constants, and and are the hyperbolic
are constants, and and are the hyperbolic 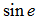 and
and 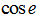 functions, respectively. Eq. (8) is solved as follows:
functions, respectively. Eq. (8) is solved as follows: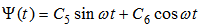 | (10) |
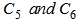 are constants. Thus, if Eq. (9) is multiplied by Eq. (10) to obtain
are constants. Thus, if Eq. (9) is multiplied by Eq. (10) to obtain 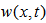 , it yields eight combined constants as:
, it yields eight combined constants as: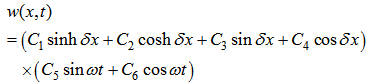 | (11) |
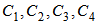 can be obtained from the boundary conditions, and
can be obtained from the boundary conditions, and 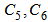 can be obtained from the initial conditions Finally, using Eq. (7) the natural frequency
can be obtained from the initial conditions Finally, using Eq. (7) the natural frequency 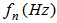 of the beam is found as follows:
of the beam is found as follows: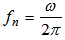 | (12) |
3. Solution of the Basic Equations
3.1. Particular Solution for C-C Beam
- The boundary conditions satisfied by a C-C beam are as follows:
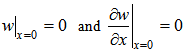 | (13) |
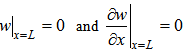 | (14) |
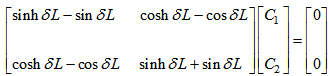 | (15) |
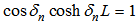 | (16) |
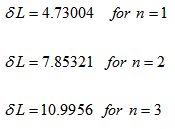 | (17) |
3.2. Particular Solution for C-F Beam
- The boundary conditions satisfied by a C-F beam are as follows:
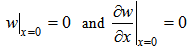 | (18) |
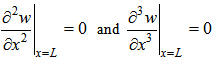 | (19) |
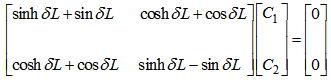 | (20) |
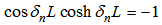 | (21) |
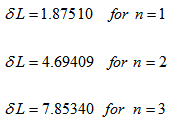 | (22) |
3.3. Particular Solution for C-SS Beam
- The boundary conditions satisfied by a C-SS beam are as follows:
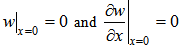 | (23) |
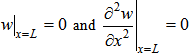 | (24) |
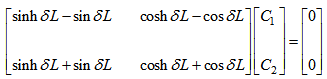 | (25) |
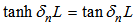 | (26) |
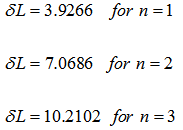 | (27) |
3.4. Particular Solution for SS-SS Beam
- The boundary conditions satisfied by a SS-SS beam are as follows:
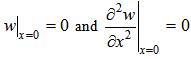 | (28) |
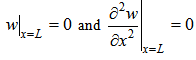 | (29) |
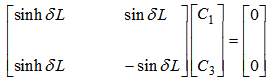 | (30) |
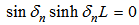 | (31) |
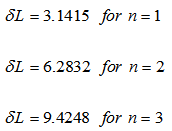 | (32) |
4. Numerical Results and Discussion
4.1. Comparative Study
- In this subsection, a comparative study was performed to validate the present numerical results. The analytical results were compared with the results of the FEM -based software called ANSYS [27]. In finite-element modeling, the beam type element is applied and meshed with 50 elements. For the first three modes
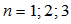 , the analytical natural frequencies,
, the analytical natural frequencies, 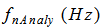 , and the FEM natural frequencies,
, and the FEM natural frequencies, 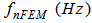 , differ by 0.223%, 0.842%, and 1.782% under C-C boundary conditions, 0.083%, 0.592%, and 1.381% under C-F boundary conditions, 0.213%, 0.784%, and 1.698% under C-SS boundary conditions, and 0.183%, 0.722%, and 1.605% under SS-SS boundary conditions, respectively. The percentages are calculated as follows:
, differ by 0.223%, 0.842%, and 1.782% under C-C boundary conditions, 0.083%, 0.592%, and 1.381% under C-F boundary conditions, 0.213%, 0.784%, and 1.698% under C-SS boundary conditions, and 0.183%, 0.722%, and 1.605% under SS-SS boundary conditions, respectively. The percentages are calculated as follows: 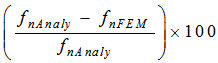 . As shown in Figure 2, the numerical results of both methods are consistent, which shows the accuracy of the present formulation.
. As shown in Figure 2, the numerical results of both methods are consistent, which shows the accuracy of the present formulation. 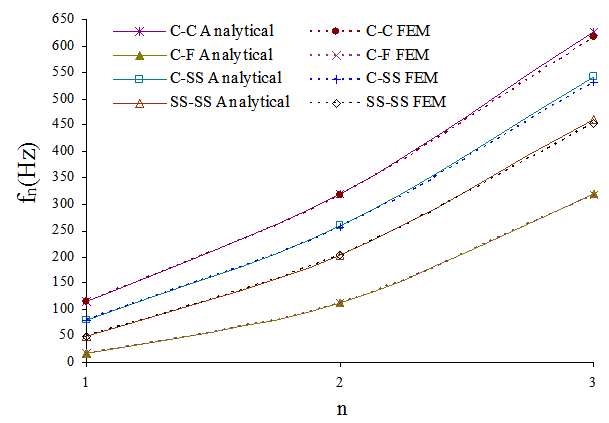 | Figure 2. Comparisons between the analytical natural frequencies and those obtained using FEM -based software called ANSYS versus mode number, n 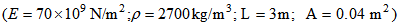 |
4.2. Free Vibration Analyses of Beams
- In this section, four studies were performed to investigate the free-vibration behaviors of square cross-sectioned aluminum beams with different geometric characteristics under four different boundary conditions. The natural frequencies were obtained and discussed for the first three modes (n=1, 2, 3), including the effects of the geometric characteristics, i.e., length and cross sectional area, and the boundary conditions.Study 1:In Figure 3, the variations in natural frequencies,
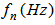 , of square cross-sectioned aluminum beams versus the first three modes (n=1, 2, 3) under four different cross sections are plotted, where
, of square cross-sectioned aluminum beams versus the first three modes (n=1, 2, 3) under four different cross sections are plotted, where 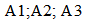 denote
denote 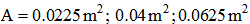 , and
, and 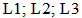 denote
denote 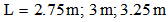 , respectively. Figure 3 shows that the natural frequencies increase with the increase in mode number. The natural frequency of the first mode number
, respectively. Figure 3 shows that the natural frequencies increase with the increase in mode number. The natural frequency of the first mode number  differs from that of the second and third mode numbers
differs from that of the second and third mode numbers  by -176% and -440% under the C-C boundary conditions, -527% and -1654% under C-F boundary conditions, -224% and -576% under C-SS boundary conditions, and -300% and -800% under SS-SS boundary conditions, respectively. The percentages were calculated as follows:
by -176% and -440% under the C-C boundary conditions, -527% and -1654% under C-F boundary conditions, -224% and -576% under C-SS boundary conditions, and -300% and -800% under SS-SS boundary conditions, respectively. The percentages were calculated as follows: 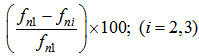 . Therefore, the variation in mode number has the largest effect on the natural frequency under C-F boundary conditions and the smallest effect under C-C boundary conditions. Study 2:Figure 3 shows that the beam has the highest natural frequencies,
. Therefore, the variation in mode number has the largest effect on the natural frequency under C-F boundary conditions and the smallest effect under C-C boundary conditions. Study 2:Figure 3 shows that the beam has the highest natural frequencies, 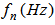 , under C-C boundary conditions and the lowest frequencies under C-F boundary conditions. To investigate the effect of the boundary condition on the natural frequencies,
, under C-C boundary conditions and the lowest frequencies under C-F boundary conditions. To investigate the effect of the boundary condition on the natural frequencies, 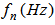 , of the beam versus the mode number, (n=1,2,3), the C-C boundary conditions were compared with the other boundary conditions. From this comparison, the following results were obtained: for n = 1, 2, and 3, i) the differences between C-C and C-F boundary conditions are 84%, 64%, and 49%, ii) the differences between C-C and C-SS boundary conditions are 31%, 19%, and 14%, and iii) the differences between C-C and SS-SS boundary conditions are 56%, 36%, and 27%, respectively. The percentages were calculated as follows:
, of the beam versus the mode number, (n=1,2,3), the C-C boundary conditions were compared with the other boundary conditions. From this comparison, the following results were obtained: for n = 1, 2, and 3, i) the differences between C-C and C-F boundary conditions are 84%, 64%, and 49%, ii) the differences between C-C and C-SS boundary conditions are 31%, 19%, and 14%, and iii) the differences between C-C and SS-SS boundary conditions are 56%, 36%, and 27%, respectively. The percentages were calculated as follows: 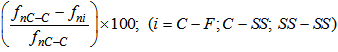 . Therefore, the effect of the type of the boundary condition decreases with the increase in mode number, n.
. Therefore, the effect of the type of the boundary condition decreases with the increase in mode number, n. 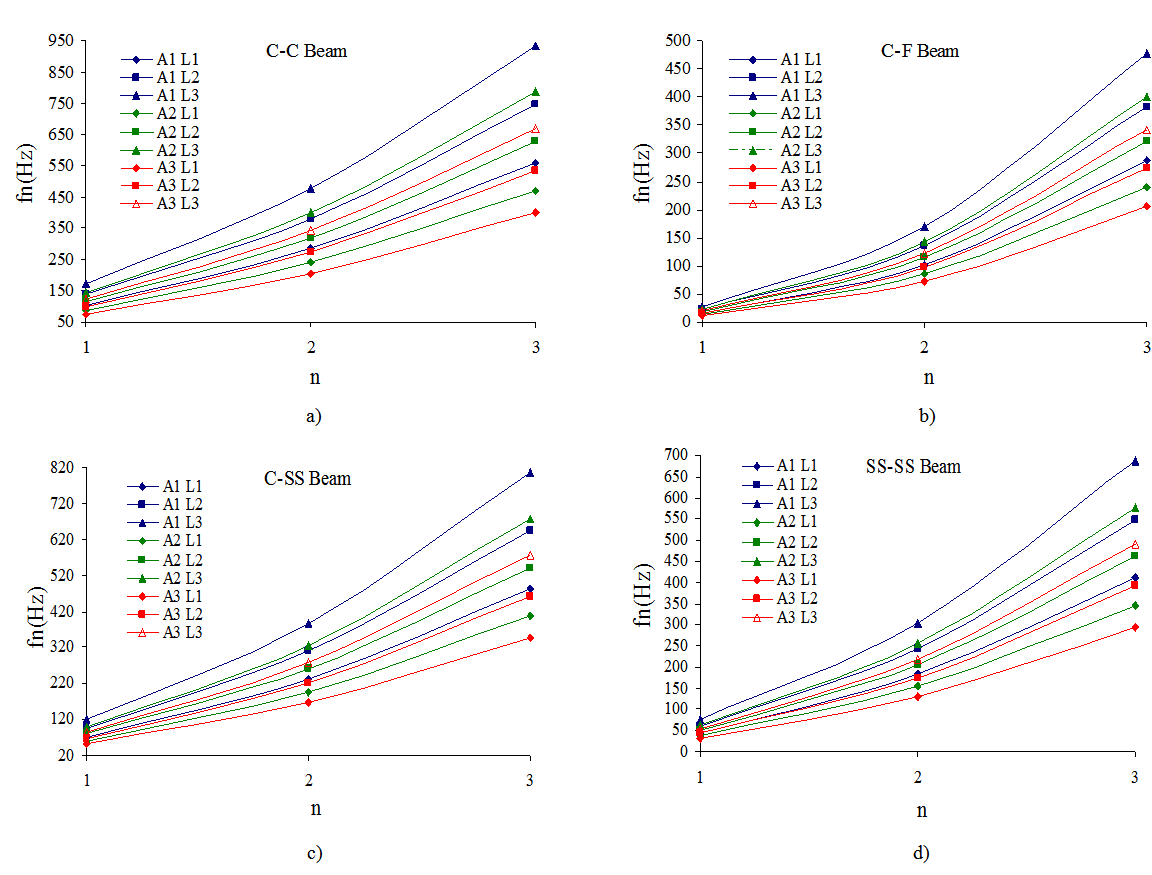 | Figure 3. Variations of the natural frequencies,  , of square cross-sectioned aluminum beams for the first three modes, (n=1,2,3) , of square cross-sectioned aluminum beams for the first three modes, (n=1,2,3)  |
 , of square cross-sectioned aluminum beams versus the length, L (m), under four different boundary conditions, where
, of square cross-sectioned aluminum beams versus the length, L (m), under four different boundary conditions, where 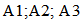 denotes
denotes 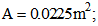
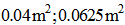 , and
, and 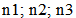 denote
denote 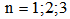 , respectively. Figure 4 obviously shows that the natural frequencies,
, respectively. Figure 4 obviously shows that the natural frequencies, 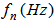 , decrease with the increase in length, L (m). To examine the effect of the variation in length of the beam on the natural frequencies, beams with identical cross sectional areas were compared. The result indicated that the variation in length had a constant effect on the natural frequencies: 15.97% and 28.40% for all cross sectional areas
, decrease with the increase in length, L (m). To examine the effect of the variation in length of the beam on the natural frequencies, beams with identical cross sectional areas were compared. The result indicated that the variation in length had a constant effect on the natural frequencies: 15.97% and 28.40% for all cross sectional areas 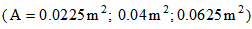 under four different boundary conditions. The percentages were calculated as follows:
under four different boundary conditions. The percentages were calculated as follows: 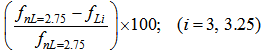 . Thus, the change in length of the beam has a constant effect on its natural frequencies for various boundary conditions and cross sectional areas.
. Thus, the change in length of the beam has a constant effect on its natural frequencies for various boundary conditions and cross sectional areas. 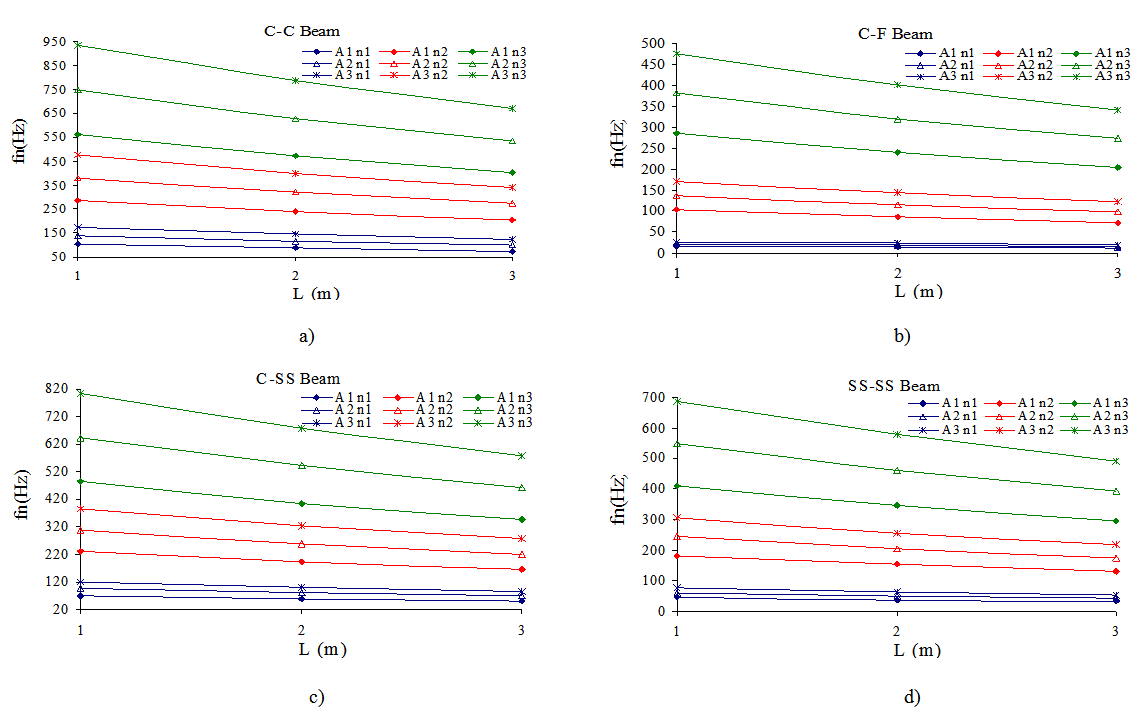 | Figure 4. Variations of the natural frequencies, 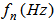 , of square cross-sectioned aluminum beams versus the length, L (m) , of square cross-sectioned aluminum beams versus the length, L (m) 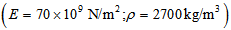 |
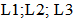 denote
denote 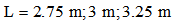 , and
, and 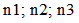 denote
denote 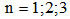 , respectively. Figure 5 shows that the natural frequencies increase with the increase in cross sectional area. To investigate the effect of the variation in cross sectional area of the beam on the natural frequencies, beams with identical lengths were compared. The result indicated that variation of the cross sectional area had a constant effect on the natural frequencies: -33.33% and -66.67% for
, respectively. Figure 5 shows that the natural frequencies increase with the increase in cross sectional area. To investigate the effect of the variation in cross sectional area of the beam on the natural frequencies, beams with identical lengths were compared. The result indicated that variation of the cross sectional area had a constant effect on the natural frequencies: -33.33% and -66.67% for 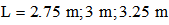 under four different boundary conditions. The percentages were calculated as follows:
under four different boundary conditions. The percentages were calculated as follows: 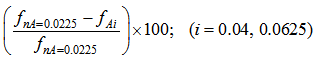 . Thus, the change in cross sectional area of the beam has a constant effect on the natural frequencies of the beam for various boundary conditions and lengths.
. Thus, the change in cross sectional area of the beam has a constant effect on the natural frequencies of the beam for various boundary conditions and lengths.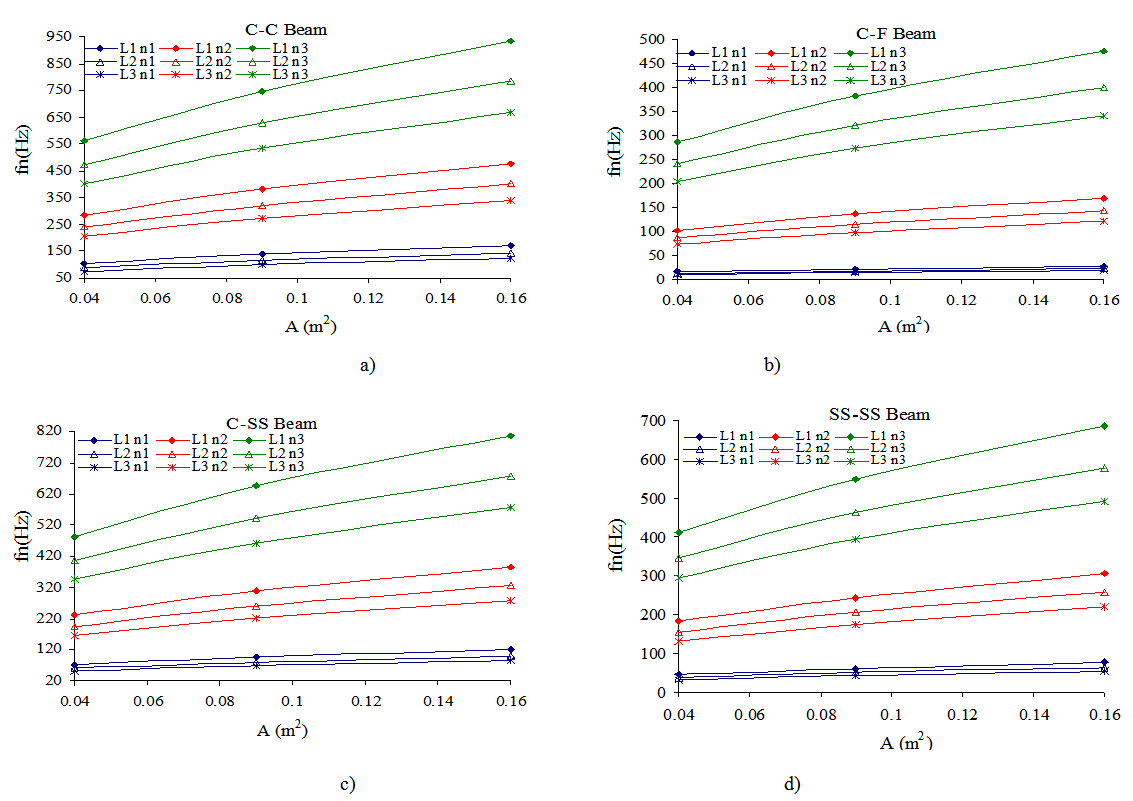 | Figure 5. Variations of the natural frequencies of square cross-sectioned aluminum beams versus the cross sectional area,  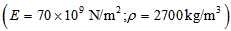 |
5. Conclusions
- In this study, the free vibration of square cross-sectioned aluminum beams is investigated analytically and numerically under four different boundary conditions. Analytical solution is carried out using Euler-Bernoulli beam theory, in which material is assumed Solutions including the effects of the geometric characteristics, i.e., length and cross sectional area, and boundary conditions are obtained and discussed for the natural frequencies of the first three modes. The following results were obtained:(1) The natural frequencies increase with the increase in mode number.(2) The change in mode numbers has the largest effect on the natural frequency under C-F boundary conditions and the smallest effect under C-C boundary conditions. (3) The beam has the highest natural frequencies under C-C boundary conditions and the lowest frequencies under C-F boundary conditions.(4) The effect of the type of the boundary condition decreases with increasing mode number.(5) The natural frequencies of the beam decrease with increasing length.(6) The change in length of the beam has a constant effect on its natural frequencies for various boundary conditions and cross sectional areas. (7) The natural frequencies of the beam increase with increasing cross sectional area.(8) The change in cross sectional area of the beam has a constant effect on the natural frequencies for various boundary conditions and lengths.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML