Hak Jin Song, Sun Jong Jon, Gi Chol Yang, Nam Chol Kim
Department of Mechanics of Materials, Kim Chaek University of Technology, Pyongyang, Korea
Correspondence to: Hak Jin Song, Department of Mechanics of Materials, Kim Chaek University of Technology, Pyongyang, Korea.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Numerical estimation of lifetime of chain plates made of 45Cr high strength steel for floodgates working in seawater has been performed by considering fatigue-creep crack initiation and hydrogen assisted crack propagation at the plate. The computational model has been validated by some related experiments on the material. First, tensile test results for the material of chain plates used for 20 years in seawater were compared with the ones for new material. According to the results, yield stress and fracture ductility of the material used for 20 years in seawater are considerably lower than the ones of new material. Second, records of operations of the floodgates were analyzed to estimate real lifetime of the chain plates and some other parameters which are necessary for computational study on the same objects. According to the records of operating history of the floodgates, average lifetime of the chain plates falls within the limit of 18~22 years. Third, lifetime of the chain plates was estimated by continuum fatigue-creep damage theory and transient analysis of the diffusion process of atomic hydrogen in the metallic lattice. Estimated lifetime of the chain plates was a little longer than the real lifetime obtained from the records because of some unexpected conditions.
Keywords:
Stress corrosion cracking, Fatigue-creep damage, Hydrogen embrittlement, Stress-assisted diffusion, Stress concentration, Lifetime
Cite this paper: Hak Jin Song, Sun Jong Jon, Gi Chol Yang, Nam Chol Kim, Lifetime Estimation of Chain Plates for Floodgates Working in Seawater by Continuum Fatigue-Creep Damage Theory and Transient Analysis of Diffusion Process of Hydrogen, International Journal of Mechanics and Applications, Vol. 4 No. 2, 2014, pp. 50-57. doi: 10.5923/j.mechanics.20140402.03.
1. Introduction
Stress-corrosion cracking (SCC) and hydrogen embrittlement (HE) are related and take main part in environment-assisted cracking, which remain incompletely understood from the view point of mechanics. Accordingly, accurate prediction of the lifetime of engineering components undergoing SCC and HE is necessary in the field of mechanical design, but still remains elusive goal.Considerable theoretical and experimental studies on SCC and HE of high strength steels were carried out for prediction and extension of lifetime of the components working in corrosion environment. There were lots of studies on behavior of hydrogen in the metallic lattice including the studies on adsorption and absorption of hydrogen at the surface of material. Many works have evaluated the diffusion process of hydrogen in the lattice using Fick’s law, and illustrated the results with some related experiments [2, 3, 5]. Some other works have studied degradation process of metals via SCC and HE mechanism, by which mechanical properties of the materials such as yield strength and fracture toughness deteriorate with the lapse of time [1, 4, 6, 7]. Degradation of mechanical properties of metals has been studied also in other directions by lots of authors, who have investigated the initiation of cracks in engineering components subjected to cyclic load from the viewpoint of fatigue-creep damage (FCD) theory [8-13]. The cracks which have been initiated by accumulation of FCD propagate across the components under the action of fatigue load. The propagation rates of the cracks will rise in corrosion environment, which shortens the lifetime of the components considerably [14-17]. In this paper, we focus on mathematical modeling of FCD and HE process of high strength steels in seawater. We have considered the lifetime of chain plates in seawater dividing into two stages. In the first stage, accumulation of FCD at the region of stress concentration leads to initiation of crack at the surface of pin hole. Continuous degradation of mechanical properties of the material in seawater was considered by FCD analysis based on Coffin-Manson equation. In the second stage, the crack initiated in the first stage propagates through the zone which has been extremely embrittled by stress assisted diffusion of hydrogen. Transient analysis of the diffusion process of hydrogen was conducted on the base of state of operation of the floodgates. Analyzing the mathematical models for these processes, consequently, we determine the lifetime of chain plates for the floodgates.For validation of the mathematical models, we perform some experimental and practical considerations for the same object.
2. Experimental and Practical Consideration
2.1. Tensile Test for the Material of the Chain Plates
The chemical composition and mechanical properties of 45Cr steel used as a material of the chain plates are shown in table 1 and 2.Table 1. Chemical composition of 45Cr steel (%)
 |
| |
|
Table 2. Mechanical properties of 45Cr steel
 |
| |
|
Figure 1 shows shape and dimensions of the chain plate considered in this paper. We had taken specimens for the tensile test from the chain plates used for 20 years in seawater and compared the test results with the ones from new material. As shown in Figure 2, collecting specimens from the old plates was performed at two positions. 5 specimens were taken at each position, which represents the place with and without stress concentration respectively. Every specimen was cut into the one with gage length of 25mm and gage diameter of 6mm. Tensile tests for both old and new materials were conducted in 25℃ air at strain rate of 10-3s-1 in accordance with NS 60-2004. The tensile test results are listed in table 3, which shows yield stress (YS) and fracture ductility (FD) of the material used for 20 years are considerably lower than the ones of new material.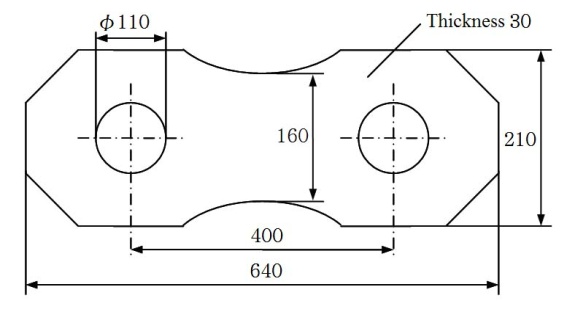 | Figure 1. Shape and dimensions of the chain plate |
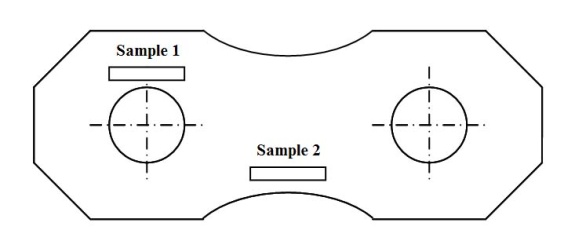 | Figure 2. Collecting specimens from the old chain plates |
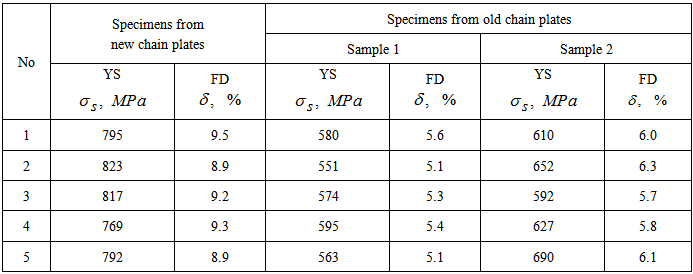
Table 3. Tensile test results for the material of the chain plate
 |
| |
|
Yield stress and fracture ductility for the specimens taken from the position of stress concentration are smaller by 28% and 42% respectively as compared with the ones for new material, 9.7% and 11% respectively as compared with the ones for the specimens taken from the position without stress concentration.
2.2. Practical Consideration for Lifetime of the Chain Plates
The floodgates considered in this paper are the ones for a barrage which crosses mouth of the river Taedong. The barrage has been constructed in 1986 and controls flood due to tide at Korean West Sea with 30 floodgates hoisted via the chain plates (Figure 3). When the water level at river Taedong is much higher than the one at Korean West Sea (especially during rainy season) the floodgates are being kept hoisted for 6~8 hours a day to drain water. 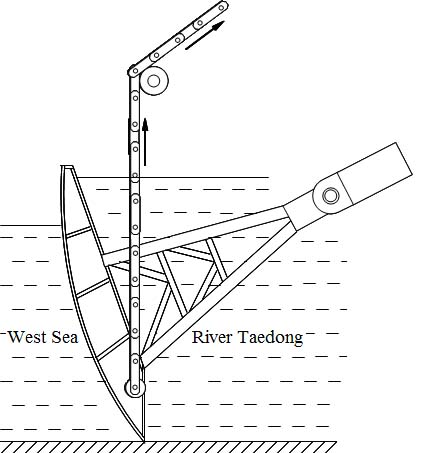 | Figure 3. Hoisting system of the floodgate |
State of operation of the floodgates as well as the state of rupture of the chain plates at the barrage were recorded thoroughly for 27 years (1986~2012) (Figure 4, 5). Record of operations of the floodgates says that maximum hoisting number of 2143 was recorded in 1990 when the amount of precipitation was great in the area. Analyzing the overall records, we can know that average hoisting number of one floodgate is about 30 per year and approximate lifetime of the chain plate is in range of 18~22 years.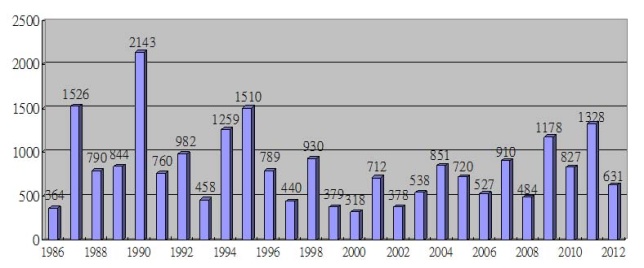 | Figure 4. Number of operations of the floodgates by year |
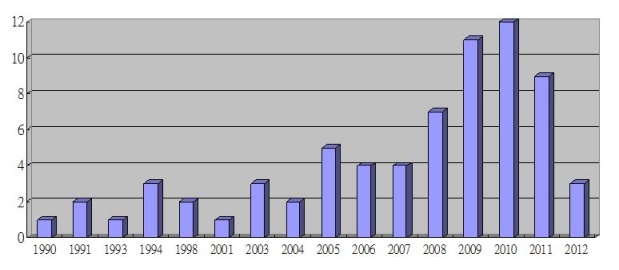 | Figure 5. Number of rupture of the chain plates by year |
3. Mathematical model
3.1. Initiation of Crack at the Place of Stress Concentration
Considering weight of the floodgate, the chain plate is subjected to a tensile load of 700KN when the floodgate is hoisted. Figure 6 shows FEA result on stress state of the chain plate subjected to this load. From the result, we can notice that the maximum tensile stress at the place of stress concentration is above 500MPa, while the stress at the place without stress concentration remains bellow 150MPa.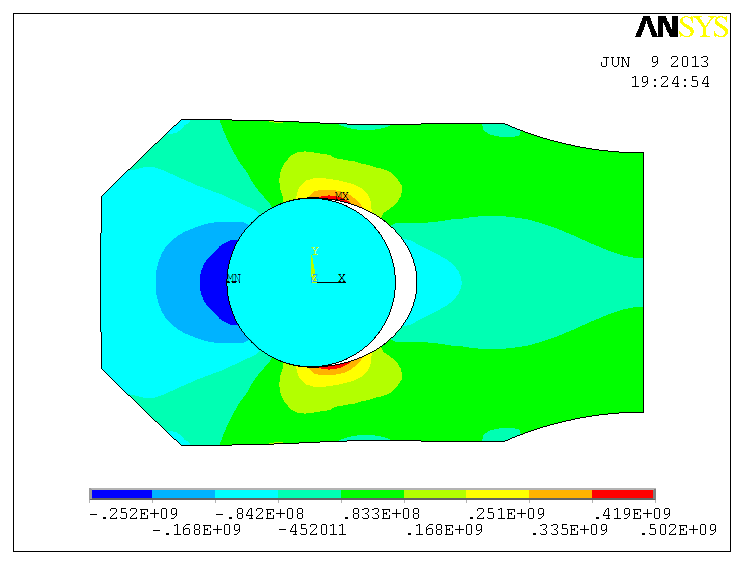 | Figure 6. FEA result on the stress state of the chain plate |
Considering that the chain plate is subjected to this load for 6~8 hours every hoisting time, FCD theory was adopted to estimate the time for initiation of crack at the place of stress concentration. Keeping in mind that yield stress of the material of the chain plate working in seawater decreases with the lapse of time and the real fatigue life of the plate is less than 103 (records show real lifetime of the chain plate is in range of 540~600), we can regard this process as low cycle fatigue. Coffin-Manson relation was hired to estimate the crack-initiation time for this low cycle fatigue process [11, 12].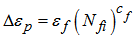 | (1) |
Here, Δεp is plastic strain range, εf and cf are fatigue ductility coefficient and fatigue ductility exponent respectively, Nfi is nominal fatigue life for given Δεp and εf.The plastic strain range Δεp was determined as the sum of plastic strains due to fatigue load and creep load, which can be obtained from the strain hardening law and Bailey-Norton law respectively [8, 10].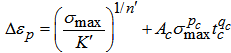 | (2) |
Here, σmax=502MPa: maximum tensile stress at the place of stress concentration,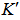 : cyclic strength coefficient,
: cyclic strength coefficient, 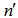 : cyclic strain hardening exponent,Ac, pc, qc: material constants related to creep characteristics, tc: creep timeConsidering that fracture ductility of the material of the chain plate working in seawater decreases with the lapse of time, fatigue ductility coefficient εf was determined as a function of time from the results of tensile tests.
: cyclic strain hardening exponent,Ac, pc, qc: material constants related to creep characteristics, tc: creep timeConsidering that fracture ductility of the material of the chain plate working in seawater decreases with the lapse of time, fatigue ductility coefficient εf was determined as a function of time from the results of tensile tests.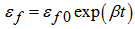 | (3) |
Here, εf0 = 0.28 is true fracture ductility of the material of brand-new chain plate and 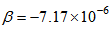 is regression coefficient.Substituting equations (2) and (3) into (1), the fatigue life of the chain plate at a hoisting number of N can be determined as
is regression coefficient.Substituting equations (2) and (3) into (1), the fatigue life of the chain plate at a hoisting number of N can be determined as 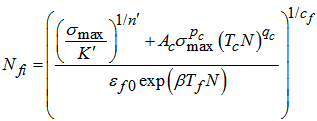 | (4) |
where Tf =292h is fatigue cycle period of the chain plate and Tc =7h is hoisting duration of the chain plate at every cycle. Considering that the plastic strain range due to creep at the chain plate and the fatigue ductility coefficient of the material change with the lapse of time N, the result of the equation (4) is not real but just the nominal fatigue life of the chain plate at the calculation step. Real fatigue life of the chain plate can be obtained from the failure criterion for FCD of the material.Fatigue and creep properties of 45Cr steel for the chain plates are listed in table 4.Table 4. Fatigue and creep properties of 45Cr steel for the chain plates
 |
| |
|
3.2. Stress-assisted Diffusion Process of Hydrogen
The crack initiated at the place of stress concentration of the chain plate by accumulation of FCD will propagate through the zone which has been extremely embrittled by hydrogen in sea water. Accurate modeling of diffusion process of hydrogen in metallic lattice of the chain plate is very important for the study on HE of the material in seawater.The stress-assisted diffusion of hydrogen in the chain plate can be analyzed using Fick’ law [5] 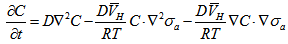 | (5) |
where 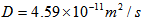 is a diffusion coefficient of hydrogen in the lattice of 45Cr steel,
is a diffusion coefficient of hydrogen in the lattice of 45Cr steel, 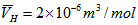 is partial molar volume of hydrogen, σa is an average principal stress at the calculation coordinates(Pa).According to the equation (5), while the floodgates are being kept shut the chain plates are subjected to non-load, hence, concentration of atomic hydrogen will be distributed evenly all over the plate. When the chain plates are hoisted to open the floodgate every plate undergoes a stress concentration around pin hole, which causes stress-assisted diffusion of hydrogen due to gradients of chemical potential. Considering that average hoisting number of the floodgates per year is 30 and hoisting time is about 7 hours at the barrage, the duration of the chain plates subjected to tensile load is just 2.5% of the duration free of the load. Short duration of the stress-assisted diffusion of hydrogen atoms emphasizes the necessity of transient analysis of the diffusion process which doesn’t reach equilibrium state in the meantime.Assuming that the chain plate is in plane stress state, the second term of right hand side of equation (5) should be zero and the third term, the gradient of average principal stress around crack tip can be determined as
is partial molar volume of hydrogen, σa is an average principal stress at the calculation coordinates(Pa).According to the equation (5), while the floodgates are being kept shut the chain plates are subjected to non-load, hence, concentration of atomic hydrogen will be distributed evenly all over the plate. When the chain plates are hoisted to open the floodgate every plate undergoes a stress concentration around pin hole, which causes stress-assisted diffusion of hydrogen due to gradients of chemical potential. Considering that average hoisting number of the floodgates per year is 30 and hoisting time is about 7 hours at the barrage, the duration of the chain plates subjected to tensile load is just 2.5% of the duration free of the load. Short duration of the stress-assisted diffusion of hydrogen atoms emphasizes the necessity of transient analysis of the diffusion process which doesn’t reach equilibrium state in the meantime.Assuming that the chain plate is in plane stress state, the second term of right hand side of equation (5) should be zero and the third term, the gradient of average principal stress around crack tip can be determined as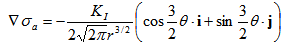 | (6) |
where KI is a stress intensity factor at the chain plate with a crack at the surface of pin hole, i and j are unit vectors in x and y directions respectively (Figure 7).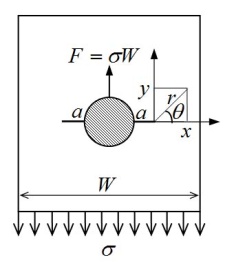 | Figure 7. Geometric model for stress analysis around crack tip |
We can’t substitute equation (6) into (5) without any considerations because there would be a plastic zone around the crack tip. Using Von Mises yield theory, effective crack size due to release of energy in the plastic zone can be calculated as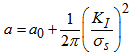 | (7) |
where a0 is a real crack size at the place of stress concentration of the chain pate.Applying linear elastic fracture theory to the chain plate with a crack at the surface of pin hole, the stress intensity factor at the plate can be derived as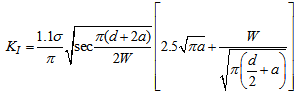 | (8) |
where 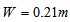 is a width of the chain plate,
is a width of the chain plate, 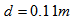 is a diameter of the pin hole and
is a diameter of the pin hole and 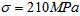 is an average tensile stress at the section of the pin hole of the chain plate.The crack initiated at the surface of pin hole of the chain plate propagates at every hoisting cycle of floodgate when the range of stress intensity factor at the plate exceeds threshold value which is degraded due to high concentration of hydrogen transported to the crack tip by stress assisted diffusion.
is an average tensile stress at the section of the pin hole of the chain plate.The crack initiated at the surface of pin hole of the chain plate propagates at every hoisting cycle of floodgate when the range of stress intensity factor at the plate exceeds threshold value which is degraded due to high concentration of hydrogen transported to the crack tip by stress assisted diffusion.
4. Results and Discussion
Real fatigue life Nf necessary for initiation of crack at the place of stress concentration of the chain plate can be determined as the hoisting cycle number at which accumulation of FCD reaches 1. This number can be determined by solving next equation.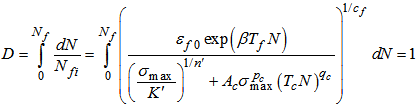 | (9) |
Fatigue life Nf = 478 was obtained by solving the nonlinear equation (9). Estimating the error of adopted material constants as 15%, the fatigue life necessary for initiation of crack at the surface of pin hole falls in limit of 410~550 (14~18 years).Considering the symmetry of the problem, the computational domain for equation (5) can be restricted to the upper right quarter of the chain plate (Figure 8). Neumann’s boundary condition is adopted for the domain considering that the chain plate is exposed in air under tensile load. Figure 8 shows initial meshing model for the computational domain. PDE Tool of MATLAB creates triangular elements in meshing process, number of which increases by 4 times at every mesh-refining procedure by dividing every side of the triangles into two. Adopted number of elements for the domain at the beginning of computation is 4832, which has been obtained after double refinements. The computation process is programmed so as to reconstruct the meshing model at every step of the crack propagation process. | Figure 8. Meshing model of computational domain |
Stress-assisted diffusion of hydrogen leads to extreme increase of concentration of hydrogen around the crack tip of the chain plate, which causes remarkable HE at the place. Cohesive law proposed in this paper is that the crack propagation occurs when the concentration of hydrogen at the end of stress assisted diffusion process (at the end of hoisting time) exceeds its threshold value, which can be determined as the concentration of hydrogen in equilibrium state of the diffusion at critical stress intensity factor KIH, the HE fracture toughness, as following equation.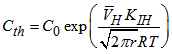 | (10) |
Here, C0 =0.255ppm is an initial concentration of diffusible hydrogen in the lattice of 45Cr steel and r is a distance between the crack tip and the position of maximum tensile stress at the plate. According to the linear elastic fracture theory, the distance r can be determined by doubling COD of the crack at the plate as following.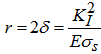 | (11) |
Figure 9 shows results of the analysis at different size of the crack which propagates across the region of stress concentration of the chain plate.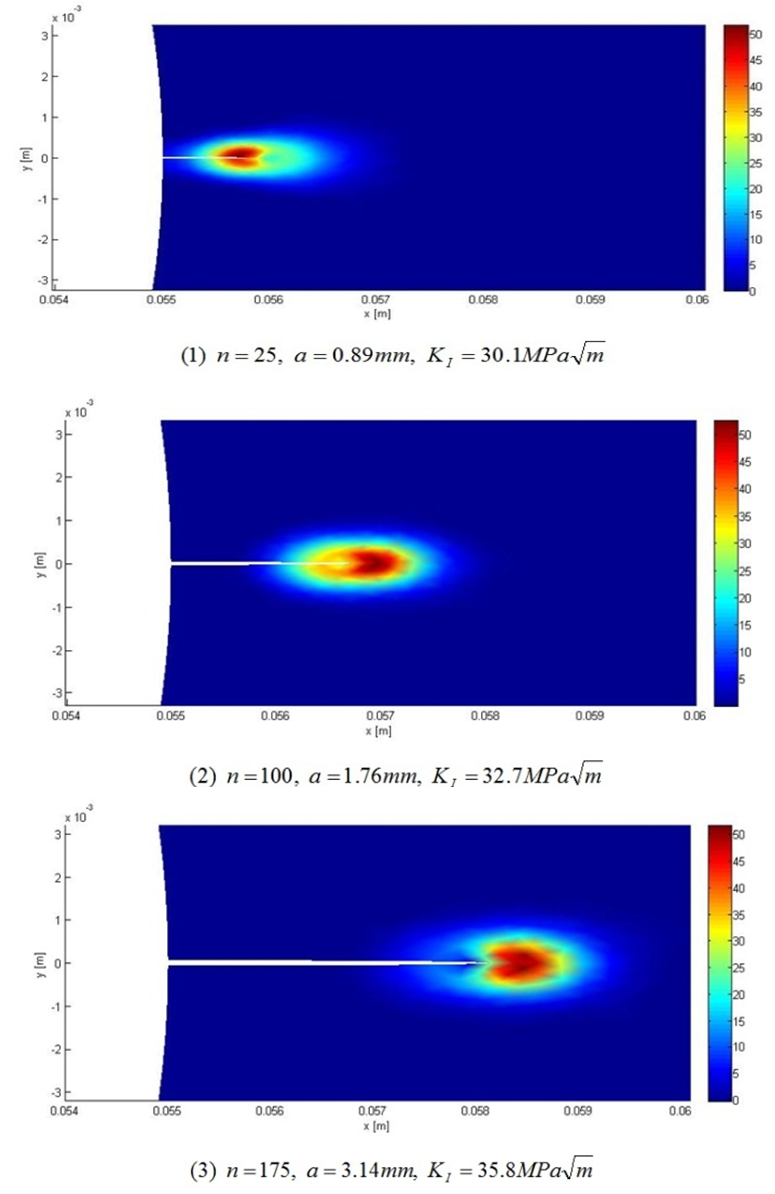 | Figure 9. Results of analysis on crack propagation process at different cycle numbers (Unit of contour bar is ppm and n shows hoisting number of the floodgate) |
According to the last result, 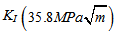 exceeds
exceeds 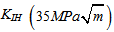 at hoisting number of 175 (length of crack is 3.14mm). Figure 10 shows an influence of number of the triangular elements of the meshing model to the result of analysis. Calculated hoisting numbers to reach the critical crack size on coarse meshing conditions (number of elements are 302 and 1208 respectively) are 159 and 172 respectively, whereas the hoisting numbers on refined meshing conditions (number of elements are 4832 and 19328 respectively) are 175 and 176 respectively. Considering that error of material constants falls within the limit of 10~15% because of unexpected conditions of the experiments, 4832 elements for the computational domain are enough to satisfy independency of meshing state.
at hoisting number of 175 (length of crack is 3.14mm). Figure 10 shows an influence of number of the triangular elements of the meshing model to the result of analysis. Calculated hoisting numbers to reach the critical crack size on coarse meshing conditions (number of elements are 302 and 1208 respectively) are 159 and 172 respectively, whereas the hoisting numbers on refined meshing conditions (number of elements are 4832 and 19328 respectively) are 175 and 176 respectively. Considering that error of material constants falls within the limit of 10~15% because of unexpected conditions of the experiments, 4832 elements for the computational domain are enough to satisfy independency of meshing state.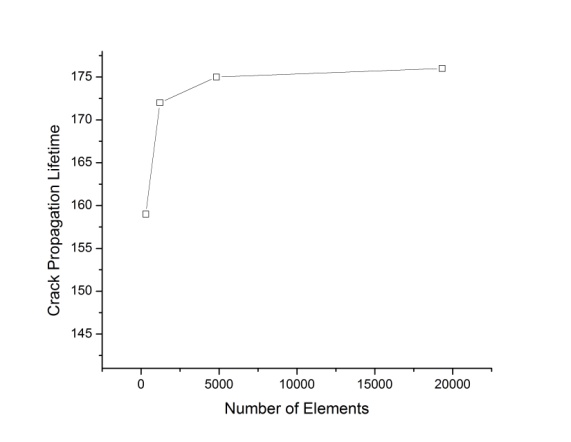 | Figure 10. Influence of number of elements on the result of analysis |
Estimating the error of adopted material constants as 15%, calculated crack propagation lifetime of the chain plate is in limit of 150~200 (5~7 years).Taking account of the lifetime for initiation of crack at the surface of pin hole, total lifetime of 45Cr steel chain plates for the floodgates of the barrage is in range of 19~25 years.Calculated lifetime of the chain plate (19~25 years) is a little longer than the real lifetime observed at the barrage (18~22 years).The reason why the calculated lifetime is longer than the observed one can be explained as bleaker operating conditions than the ones estimated in the calculation. Various conditions such as poor lubricating state at friction slot of the floodgate, asynchronous operation of left and right chains, effect of billows etc. can increase tensile stress around the crack tip together with concentration of hydrogen and crack propagation rate, consequently shorten the lifetime for both initiation and propagation of the crack at the chain plate.Taking account of these kinds of conditions, we can expect reliable estimation of lifetime for the chain plates working in seawater.
5. Conclusions
We have performed some experimental and computational study to estimate lifetime of chain plates for floodgates working in seawater. The tensile test results show that yield stress and fracture ductility of the material used in seawater for 20 years are considerably lower than the ones of new material. Yield stress and fracture ductility for the specimens taken from the place of stress concentration of the chain plates are smaller by 28% and 42% respectively as compared with the ones for new material, 9.7% and 11% respectively as compared with the ones for the specimens taken from the place without stress concentration.Records of operating history at the barrage show that average hoisting number of one floodgate is about 30 per year and practical lifetime of the chain plate is in limit of 18~22 years, which is a little smaller than the calculated one (19~25 years) due to bleaker operating conditions of the floodgates at the barrage than the ones considered in calculation.Good agreement between computational models and the experimental results validates hydrogen assisted failure mechanism of steel structures in sea water.
ACKNOWLEDGEMENTS
H. J. Song is grateful to Hyon Ho Sin the chief of technical section of the barrage for the bulky records of operating history of the floodgates for 27 years and for the materials which are necessary for tensile tests.
References
| [1] | B. Kareen, Efeects of selected media on corrosion behavior of mild steel, Advanced Materials Research, Elsevier, Vol.62~64(2009), 305~310. |
| [2] | E. Fallahmohammadi, Measurement of lattice and apparent diffusion coefficient of hydrogen in X65 and F22 pipeline steels, Int. J. of Hydrogen Energy, Elsevier, 38(2013), 2531~2543. |
| [3] | Magnus S., Effect of microstructure and temperature on hidrogen diffusion and trapping in x70 grade pipeline steel and its weldment, Materials Science and Engineering A, Elsevier, 427(2009), 371~379. |
| [4] | Julian J. Rimoi, A computational model for intergranular stress corrosion cracking, Ph.D. thesis of California Institute of Technology, 2009, 5. |
| [5] | Vigdis Olden, FE Simulation of Hydrogen Diffusion in Duplex Stainless Steel – Influence of Phase Shape, an Size and Embeded Deffects, Proceedings of the Twenty-third (2013) International Offshore and Polar Engineering Anchorage, Alaska, June 30 – July 5, 2013. |
| [6] | Mioara E. S., Hydrogen Embrittlement of Ferrous Materials, Ph.D. thesis of Brussel University, Belgium, 2006, 143~176. |
| [7] | L. Cascini, An integrated approach to durability design of steel structures against atmospheric corrosion, Key Engineerin Materials, Trans Tech Publications, Vol. 385~387 (2008), 657~660. |
| [8] | S. Kwofie, H. D. Chandler, Fatigue life prediction under conditions where cyclic creep-fatigue interaction occurs, International J. of Fatigue, Elsevier, 29(2007), 2117~2124. |
| [9] | R. Rajendran, J. K. Paik, Creep life prediction of high strength steel plate, Materials and Design, Elsevier, 29(2008), 427~435. |
| [10] | K. Harry, Creep analysis, New York, John Wiley & Sons, 1980. |
| [11] | L.F. Coffin Jr., J. Eng. Mater. Tech. ASME 76 (1954), 931. |
| [12] | S.S. Manson, NASA Technical Note 2933, Cleveland, 1954. |
| [13] | Thierry Palin-Luc, Fatigue crack initiation and growth on a steel in the very high cycle regime with sea water corrosion, Engineering Fracture Mechanics, Elsevier, 77(2010), 1953~1962. |
| [14] | Donghwan K., Corrosion Fatigue Crack Propagation of High-Strength Steel HSB800 in a Seawater Environment, Procedia Engineering, Elsevier, 10(2011), 1170~1175. |
| [15] | Wonbeom K., Evaluation of corrosion fatigue crack propagation characteristics of TMCP steel in synthetic seawater under cathodic protection, Advanced Materials Research, Elsevier, Vol.26~28(2007), 617~623. |
| [16] | Ruben Perez Mora, Very high cycle fatigue analysis of high strength steel with corrosion pitting, Key Engineerin Materials, Trans Tech Publications, Vol.449(2010), 104~113. |
| [17] | M. Knop, Effects of cycle frequency on corrosion-fatigue crack growth in cathodically protected high-strength steels, Procedia Engineering, Elsevier, 2(2010), 1243~1252. |






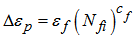
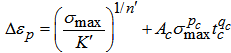
 : cyclic strength coefficient,
: cyclic strength coefficient, 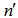 : cyclic strain hardening exponent,Ac, pc, qc: material constants related to creep characteristics, tc: creep timeConsidering that fracture ductility of the material of the chain plate working in seawater decreases with the lapse of time, fatigue ductility coefficient εf was determined as a function of time from the results of tensile tests.
: cyclic strain hardening exponent,Ac, pc, qc: material constants related to creep characteristics, tc: creep timeConsidering that fracture ductility of the material of the chain plate working in seawater decreases with the lapse of time, fatigue ductility coefficient εf was determined as a function of time from the results of tensile tests.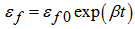
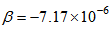 is regression coefficient.Substituting equations (2) and (3) into (1), the fatigue life of the chain plate at a hoisting number of N can be determined as
is regression coefficient.Substituting equations (2) and (3) into (1), the fatigue life of the chain plate at a hoisting number of N can be determined as 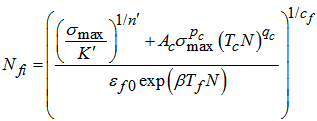
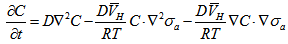
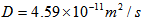 is a diffusion coefficient of hydrogen in the lattice of 45Cr steel,
is a diffusion coefficient of hydrogen in the lattice of 45Cr steel, 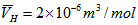 is partial molar volume of hydrogen, σa is an average principal stress at the calculation coordinates(Pa).According to the equation (5), while the floodgates are being kept shut the chain plates are subjected to non-load, hence, concentration of atomic hydrogen will be distributed evenly all over the plate. When the chain plates are hoisted to open the floodgate every plate undergoes a stress concentration around pin hole, which causes stress-assisted diffusion of hydrogen due to gradients of chemical potential. Considering that average hoisting number of the floodgates per year is 30 and hoisting time is about 7 hours at the barrage, the duration of the chain plates subjected to tensile load is just 2.5% of the duration free of the load. Short duration of the stress-assisted diffusion of hydrogen atoms emphasizes the necessity of transient analysis of the diffusion process which doesn’t reach equilibrium state in the meantime.Assuming that the chain plate is in plane stress state, the second term of right hand side of equation (5) should be zero and the third term, the gradient of average principal stress around crack tip can be determined as
is partial molar volume of hydrogen, σa is an average principal stress at the calculation coordinates(Pa).According to the equation (5), while the floodgates are being kept shut the chain plates are subjected to non-load, hence, concentration of atomic hydrogen will be distributed evenly all over the plate. When the chain plates are hoisted to open the floodgate every plate undergoes a stress concentration around pin hole, which causes stress-assisted diffusion of hydrogen due to gradients of chemical potential. Considering that average hoisting number of the floodgates per year is 30 and hoisting time is about 7 hours at the barrage, the duration of the chain plates subjected to tensile load is just 2.5% of the duration free of the load. Short duration of the stress-assisted diffusion of hydrogen atoms emphasizes the necessity of transient analysis of the diffusion process which doesn’t reach equilibrium state in the meantime.Assuming that the chain plate is in plane stress state, the second term of right hand side of equation (5) should be zero and the third term, the gradient of average principal stress around crack tip can be determined as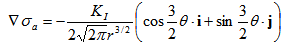

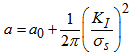
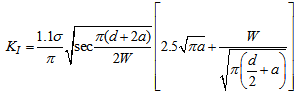
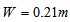 is a width of the chain plate,
is a width of the chain plate, 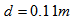 is a diameter of the pin hole and
is a diameter of the pin hole and 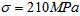 is an average tensile stress at the section of the pin hole of the chain plate.The crack initiated at the surface of pin hole of the chain plate propagates at every hoisting cycle of floodgate when the range of stress intensity factor at the plate exceeds threshold value which is degraded due to high concentration of hydrogen transported to the crack tip by stress assisted diffusion.
is an average tensile stress at the section of the pin hole of the chain plate.The crack initiated at the surface of pin hole of the chain plate propagates at every hoisting cycle of floodgate when the range of stress intensity factor at the plate exceeds threshold value which is degraded due to high concentration of hydrogen transported to the crack tip by stress assisted diffusion.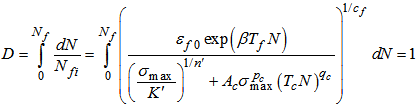

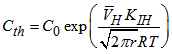
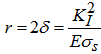

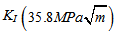 exceeds
exceeds 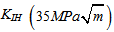 at hoisting number of 175 (length of crack is 3.14mm). Figure 10 shows an influence of number of the triangular elements of the meshing model to the result of analysis. Calculated hoisting numbers to reach the critical crack size on coarse meshing conditions (number of elements are 302 and 1208 respectively) are 159 and 172 respectively, whereas the hoisting numbers on refined meshing conditions (number of elements are 4832 and 19328 respectively) are 175 and 176 respectively. Considering that error of material constants falls within the limit of 10~15% because of unexpected conditions of the experiments, 4832 elements for the computational domain are enough to satisfy independency of meshing state.
at hoisting number of 175 (length of crack is 3.14mm). Figure 10 shows an influence of number of the triangular elements of the meshing model to the result of analysis. Calculated hoisting numbers to reach the critical crack size on coarse meshing conditions (number of elements are 302 and 1208 respectively) are 159 and 172 respectively, whereas the hoisting numbers on refined meshing conditions (number of elements are 4832 and 19328 respectively) are 175 and 176 respectively. Considering that error of material constants falls within the limit of 10~15% because of unexpected conditions of the experiments, 4832 elements for the computational domain are enough to satisfy independency of meshing state.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML


