-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Mechanics and Applications
p-ISSN: 2165-9281 e-ISSN: 2165-9303
2013; 3(6): 145-154
doi:10.5923/j.mechanics.20130306.02
Wave Propagation in Thermo-piezoelectric Solid bar of Circular Cross-Section Immersed in Fluid
P. Ponnusamy
Department of Mathematics, Government Arts College (Autonomous), Coimbatore, Tamil Nadu, 641 018, India
Correspondence to: P. Ponnusamy, Department of Mathematics, Government Arts College (Autonomous), Coimbatore, Tamil Nadu, 641 018, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Wave propagation in a thermo-piezoelectric solid bar of circular cross-section immersed in fluid is studied using three-dimensional theory of thermo-piezoelectricity. Three displacement potential functions are introduced to uncouple the equation of motion, electric and heat conductions. The frequency equations are obtained for longitudinal and flexural modes of vibration and are studied numerically for heat conducted PZT-4 material immersed in fluid. Computed non-dimensional wave numbers are presented in the form of dispersion curves. The secant method is applied to obtain the roots of the frequency equation. Comparison of dispersion curves between the non-dimensional wave numbers of thermo-piezoelectric cylindrical bar of circular cross-section in space and immersed in fluid. By framing proper mathematical formulation the same method can be applied to any vibrational problem of this kind.
Keywords: Piezoelectric cylinder/plates, Solid-fluid interaction, Thermal cylinders/plates, Sensors, Vibration, Stress analysis
Cite this paper: P. Ponnusamy, Wave Propagation in Thermo-piezoelectric Solid bar of Circular Cross-Section Immersed in Fluid, International Journal of Mechanics and Applications, Vol. 3 No. 6, 2013, pp. 145-154. doi: 10.5923/j.mechanics.20130306.02.
Article Outline
1. Introduction
- The piezoelectricity was discovered by the brothers Curie in 1880 (Curie and Curie, 1880). In general piezoelectric materials are physically strong and chemically inert, and they are relatively inexpensive to manufacture. The composition, shape and dimension of piezoelectric ceramic elements can be tailored to meet the requirements of a specific purpose. Ceramics manufactured from formulations of lead zirconate/lead titanate exhibit greater sensitivity and higher operating temperatures, relative to ceramics of other compositions and the materials PZT-4 are most widely used piezoelectric ceramics.In recent years, polymers piezoelectric materials have been used in numerous fields taking advantage of the flexible characteristics of these polymers. Some of the applications of these polymers include audio device- microphones, high frequency speakers, tone generators and acoustic modems; Pressure switches-position switches, accelerometers, impact detectors, flow meters and load cells; Actuators-electronic fans and high shutters. Since piezoelectric polymers allow their use in a multitude of compositions and geometrical shapes for a large variety of applications from transducers in acoustics, ultrasonic’s and hydrophone applications to resonators in band pass filters, power supplies, delay lines, medical scans and some industrial non-destructive testing instruments.Early studies in elastic wave propagation in cylindrical waveguides are mostly concerned with isotropic cylinders. Wave propagation in infinitely long cylinders have been investigated since the time of Pochhamer and Chree. Detailed account of the historical development of the problem has been given by Meeker and Meitzler[1]. The propagation of compressional elastic waves along an anisotropic circular cylinder with hexagonal symmetry was first studied by Morse[2]. Two-part study by Mirsky[3] was devoted to the problem of longitudinal waves propagation in transversely isotropic circular cylinders using an approach based on potential functions.Theoretical studies on electroelastic wave propagation in anisotropic piezoceramic cylinders have also been pursued for many years. The approach usually applied for piezoelectric solids is the simplification of Maxwell’s equations by neglecting magnetic effects, conduction, free charges, and displacement currents. Studies by Tiersten[4] should be mentioned among the early notable contributions to the topic of the mechanics of piezoelectric solids. Electoelastic governing equations of piezoelectric materials are presented by Parton and Kudryavtsev[5]. Shul’ga[6] studied the propagation of axisymmetric and non-axisymmetric waves in anisotropic piezoceramic cylinders with various prepolarization directions and boundary conditions.Paul and Venkatesan[7,8] studied the wave propagation in infinite piezoelectric solid cylinders of arbitrary cross-section using Fourier expansion collocation method, formulated by Nagaya[9]. Rajapakse and Zhou[10] solved the coupled electrostatic equations for a long piezoceramic cylinder by applying Fourier integral transforms. Paper by Wang[11] should be mentioned among the studies of cylindrical shells with a piezoelectric coat. Ebenezer and Ramesh[12] analysed axially polarized piezoelectric cylinders with arbitrary boundary conditions on the flat surfaces using the Bessel series. Berg et al.[13] assumed electric field not be constant over the thickness of piezoceramic cylindrical shells. Later Botta and Cerri[14] extended this approach and compared their results with those in which the effect of variable electric potential was not considered. Kim and Lee[15] studied piezoelectric cylindrical transducers with radial polarization and compared their results with those obtained experimentally and numerically by the finite-element method. The wave propagation in elastic solid has been discussed extensively in details by Graff[16] and Achenbach[17].Sinha et al.[18] have studied the axisymmetric wave propagation in circular cylindrical shell immersed in a fluid, in two parts. In Part I, the theoretical analysis of the propagation modes is discussed and in Part II, the axisymmetric modes excluding tensional modes are obtained theoretically and experimentally and are compared. Berliner and Solecki[19] have studied the wave propagation in a fluid loaded transversely isotropic cylinder. In that paper, Part I consists of the analytical formulation of the frequency equation of the coupled system consisting of the cylinder with inner and outer fluid and Part II gives the numerical results. Guo and Sun[20] discussed the propagation of Bleustein-Gulyaev wave in 6mm piezoelectric materials loaded with viscous liquid using the theory of continuum mechanics. Qian et al.[21] analysed the propagation of Bleustein-Gulyaev waves in 6mm piezoelectric materials loaded with a viscous liquid layer of finite thickness. Baghdasaryan and Danoyan[22] studied about the electro-magneto-elastic waves. Grinchenko et al.[23] investigated the planar vibrations of rectangular piezoceramic plates.Venkatesan and Ponnusamy[24, 25] studied the wave propagation in solid and generalized solid cylinder of arbitrary cross-sections immersed in fluid using the Fourier expansion collocation method. Dayal[26] investigated the free vibrations of a fluid loaded transversely isotropic rod based on uncoupling the radial and axial wave equations by introducing scalar and vector potentials. Nagy[27] studied the propagation of longitudinal guided waves in fluid-loaded transversely isotropic rod based on the superposition of partial waves. Guided waves in a transversely isotropic cylinder immersed in a fluid were analysed by Ahmad[28]. Ponnusamy[29] and later with Rajagopal[30] have studied, the wave propagation in a generalized thermo elastic solid cylinder and homogeneous transversely isotropic solid cylinder of arbitrary cross-sections respectively using the Fourier expansion collocation method.The present article is aimed to study the wave propagation in a thermo-piezoelectric solid bar of circular cross-section immersed in fluid. The frequency equations are obtained from the thermal solid-fluid boundary conditions. The computed non-dimensional wave numbers are plotted in the form of dispersion curves for longitudinal and flexural modes of vibrations for the material PZT-4. To discuss the accuracy of the present result with the existing literature, the frequency equations obtained by omitting heat conduction equation matches well with the frequency equations obtained by Ponnusamy[31].
2. Formulation of the Problem
- We consider a homogeneous transversely isotropic piezoelectric thermally conducting elastic bar of infinite length immersed in fluid with uniform temperature
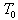 in the undistributed state initially,
in the undistributed state initially, 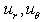 and
and 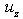 are respectively the radial, circumferential and axial displacement components, which are defined through the cylindrical coordinates
are respectively the radial, circumferential and axial displacement components, which are defined through the cylindrical coordinates 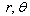 and
and 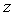 . The equations of motion, heat conduction and electric potentials in the absence of body force are
. The equations of motion, heat conduction and electric potentials in the absence of body force are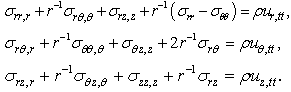 | (1) |
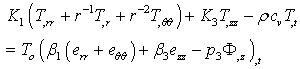 | (2) |
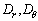 and
and 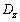 satisfy the Gaussian equation is
satisfy the Gaussian equation is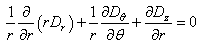 | (3) |
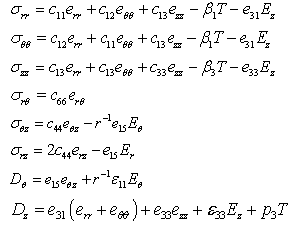 | (4) |
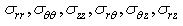 are the stress components,
are the stress components, 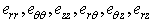 are the strain components, T is the temperature change about the equilibrium temperature
are the strain components, T is the temperature change about the equilibrium temperature 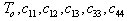 and
and 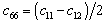 are the five elastic constants,
are the five elastic constants, 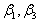 and
and 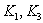 respectively thermal expansion coefficients and thermal conductivities along and perpendicular to the symmetry,
respectively thermal expansion coefficients and thermal conductivities along and perpendicular to the symmetry, 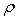 is the mass density,
is the mass density, 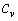 is the specific heat capacity ,
is the specific heat capacity , 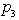 is the pyroelectric effect. The strain
is the pyroelectric effect. The strain 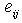 related to the displacements are given by
related to the displacements are given by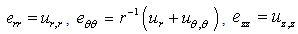 | (5a) |
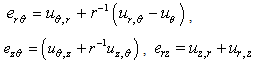 | (5b) |
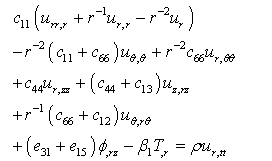 | (6a) |
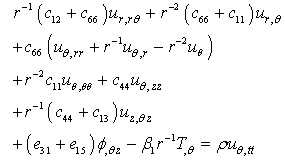 | (6b) |
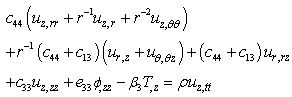 | (6c) |
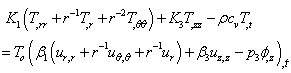 | (6d) |
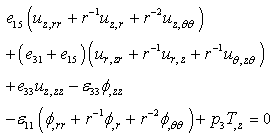 | (6e) |
3. Solutions of the Field Equation
- To obtain the propagation of harmonic waves in thermo-piezoelectric circular bar, we assume the solutions of the displacement components to be expressed in terms of derivatives of potentials are taken from Paul[32]. Thus, we seek the solution of the Eq. (6) in the form of Paul[32] are
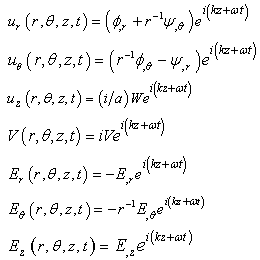 | (7) |
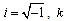 is the wave number,
is the wave number,  is the angular frequency,
is the angular frequency, 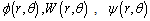 and
and 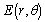 are the displacement potentials,
are the displacement potentials, 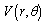 is the electric potentials,
is the electric potentials, 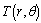 is the temperature change and
is the temperature change and 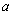 is the geometrical parameter of the bar. By introducing the dimensionless quantities such as
is the geometrical parameter of the bar. By introducing the dimensionless quantities such as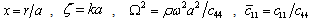 ,
, 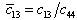 ,
, 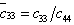 ,
, 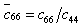 ,
,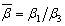 ,
,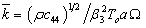 ,
, 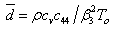 ,
, 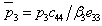 and substituting Eq.(7) in Eq.(6), we obtain
and substituting Eq.(7) in Eq.(6), we obtain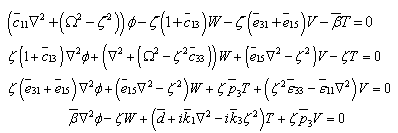 | (8) |
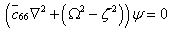 | (9) |
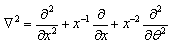 .
.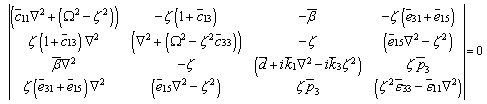 | (10) |
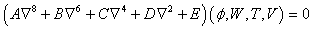 | (11) |
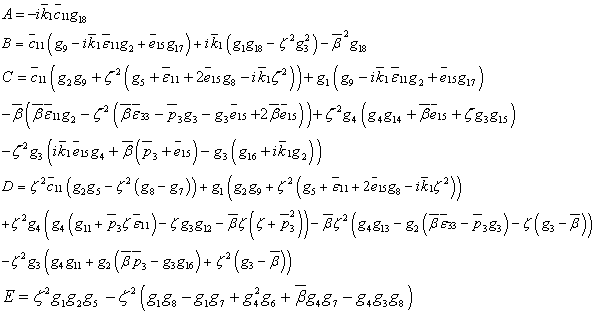 in which
in which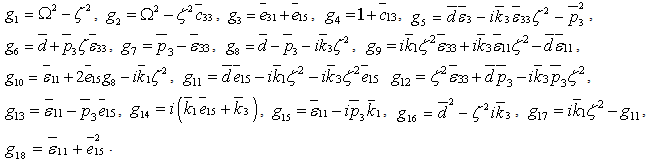 Factorizing the relation given in Eq.(11) into biquadratic equation for
Factorizing the relation given in Eq.(11) into biquadratic equation for 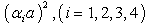 , the solutions for the symmetric modes are obtained as
, the solutions for the symmetric modes are obtained as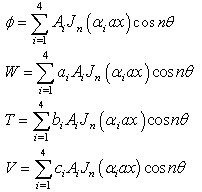 | (12) |
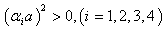 are the roots of the algebraic equation
are the roots of the algebraic equation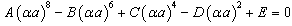 | (13) |
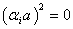 is not considered here, since
is not considered here, since 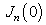 is zero, except for
is zero, except for 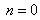 . The Bessel function
. The Bessel function 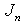 is used when the roots
is used when the roots 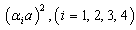 are real or complex and the modified Bessel function
are real or complex and the modified Bessel function 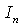 is used when the roots
is used when the roots 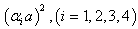 are imaginary.The constants
are imaginary.The constants 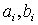 and
and 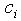 defined in Eq.(12) can be calculated from the equations
defined in Eq.(12) can be calculated from the equations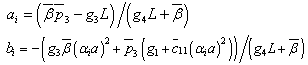 Solving Eq.(9), the solution to the symmetric mode is obtained as
Solving Eq.(9), the solution to the symmetric mode is obtained as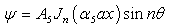 | (15) |
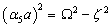 . If
. If 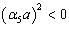 , the Bessel function
, the Bessel function 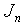 is replaced by the modified Bessel function
is replaced by the modified Bessel function 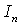 .
. 4. Equations of Motion of the Fluid
- In cylindrical polar coordinates
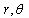 and
and 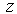 the acoustic pressure and radial displacement equation of motion for an invicid fluid are of the form Achenbach[17]
the acoustic pressure and radial displacement equation of motion for an invicid fluid are of the form Achenbach[17]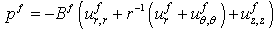 | (16) |
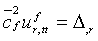 | (17) |
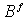 is the adiabatic bulk modulus,
is the adiabatic bulk modulus, 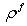 is the density,
is the density, 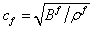 is the acoustic phase velocity in the fluid, and
is the acoustic phase velocity in the fluid, and 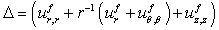 | (18) |
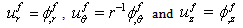 | (19) |
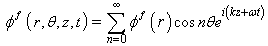 | (20) |
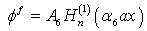 | (21) |
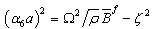 , in which
, in which 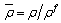 ,
, 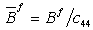 ,
, 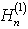 is the Hankel function of first kind. If
is the Hankel function of first kind. If 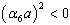 , then the Hankel function of first kind is to be replaceb by
, then the Hankel function of first kind is to be replaceb by 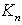 , where
, where 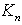 is the modified Bessel function of the second kind. By substituting Eq. (20) in Eq. (16) along with Eq. (21), the acoustic pressure for the fluid can be expressed as
is the modified Bessel function of the second kind. By substituting Eq. (20) in Eq. (16) along with Eq. (21), the acoustic pressure for the fluid can be expressed as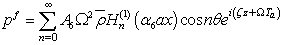 | (22) |
5. Boundary Conditions and Frequency Equations
- In this problem, the free vibration of transversely isotropic thermo-piezoelectric solid bar of circular cross-section immersed in fluid is considered. In the solid-fluid interface problems, the normal stress of the bar is equal to the negative of the pressure exerted by the fluid and the displacement component in the normal direction of the lateral surface of the cylinder is equal to the displacement of the fluid in the same direction. These conditions are due to the continuity of the stresses and displacements of the solid and fluid boundaries. Since the inviscid fluid cannot sustain shear stress, the shear stress of the outer fluid is equal to zero.For the solid-fluid problems, the continuity conditions require that the displacement components, the surface stress components, electric potential and thermal field must be equal. The boundary conditions can be written as
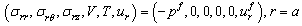 | (23) |
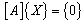 | (24) |
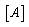 is a
is a 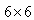 matrix of unknown wave amplitudes, and
matrix of unknown wave amplitudes, and 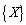 is an
is an 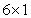 column vector of the unknown amplitude coefficients
column vector of the unknown amplitude coefficients 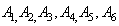 . The components of
. The components of 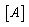 are defined in the Appendix A. The solution of Eq. (24) is nontrivial when the determinant of the coefficient of the wave amplitudes
are defined in the Appendix A. The solution of Eq. (24) is nontrivial when the determinant of the coefficient of the wave amplitudes 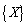 vanishes, that is
vanishes, that is 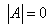 | (25) |
6. Particular Case
- The frequency equation for a piezoelectric bar of circular cross-section is obtained by omitting the fluid and thermal field in the corresponding equations and solutions. The frequency equations obtained in this method matches well with the frequency equations of Paul and Raju[33] which shows the exactness of this method. Also, to discuss the accuracy of the present result with the existing literature, the frequency equations obtained by omitting heat conduction equation matches well with the frequency equations obtained by Ponnusamy[31].
7. Numerical Results and Discussion
- The frequency equation given in Eq. (24) is transcendental in nature with unknown frequency and wave number. The solutions of the frequency equation are obtained numerically by fixing the wave number. The material chosen for the numerical calculation is PZT-4. The material properties of PZT-4 taken form Berlincourt et al.[34] are used for the numerical calculation and are given below:
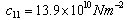 ,
, 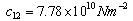 ,
, 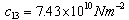 ,
, 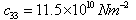 ,
, 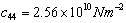 ,
, 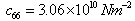 ,
, 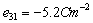 ,
, 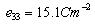 ,
, 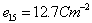 ,
, 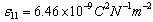 ,
, 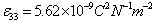 ,
, 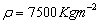 . The thermal properties such as thermal expansion coefficients
. The thermal properties such as thermal expansion coefficients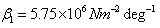 ,
, 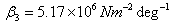 , thermal conductivities
, thermal conductivities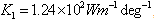 ,
, 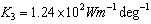 , specific heat capacity
, specific heat capacity 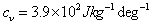 and the reference temperature
and the reference temperature 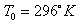 , the pyroelectric constant
, the pyroelectric constant 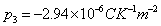 and for fluid the density
and for fluid the density 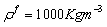 , phase velocity
, phase velocity 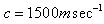 .In this problem, two kinds of basic independent modes of wave propagation have been considered, namely, the longitudinal and flexural modes. By choosing respectively n=0 and n=1, we can obtain the non-dimensional frequencies of longitudinal and flexural modes of vibrations.
.In this problem, two kinds of basic independent modes of wave propagation have been considered, namely, the longitudinal and flexural modes. By choosing respectively n=0 and n=1, we can obtain the non-dimensional frequencies of longitudinal and flexural modes of vibrations. 7.1. Dispersion Curves
- The results of longitudinal and flexural modes are plotted in the form of dispersion curves. The notation used in the figures namely, Lm, TLm and IFLm denotes the longitudinal modes of piezoelectric cylinder in space, thermo piezoelectric cylinder in space and immersed in fluid. Similarly the notation Fm, TFm and IFFm respectively denotes the flexural modes of piezoelectric cylinder in space, thermo-piezoelectric cylinder in space and immersed in fluid. The 1 refer to the first mode, 2 refer the second mode and so on in all the dispersion curves. A graph is drawn between non-dimensional frequencies
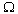 versus dimensionless wave number for a thermo- piezoelectric cylindrical bar for longitudinal modes of vibrations and is shown in Figure 1. From Figure 1, it is observed that the dimensionless wave number increases and decreases simultaneously as non-dimensional frequency increases for any modes of vibration. Also it is observed that as modes of vibration increases the dimensionless wave number increases with respect to its non-dimensional frequency.
versus dimensionless wave number for a thermo- piezoelectric cylindrical bar for longitudinal modes of vibrations and is shown in Figure 1. From Figure 1, it is observed that the dimensionless wave number increases and decreases simultaneously as non-dimensional frequency increases for any modes of vibration. Also it is observed that as modes of vibration increases the dimensionless wave number increases with respect to its non-dimensional frequency.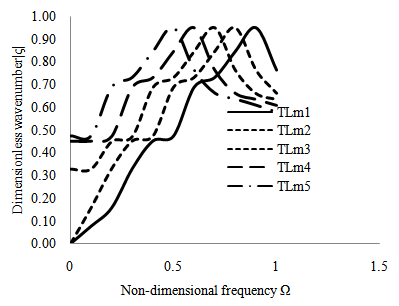 | Figure 1. Non-dimensional frequency Ω versus dimensionless wave number for a thermo-piezoelectric cylindrical bar for longitudinal modes of vibration |
 versus dimensionless wave number for a thermo-piezoelectric cylindrical bar for flexural modes of vibration and is shown in Figure 2. From Figure 2, it is observed that the dimensionless wave number increases as non-dimensional frequency increases for all modes of vibration. Also it is observed that the dimensionless wave number increases as modes of vibration increases.
versus dimensionless wave number for a thermo-piezoelectric cylindrical bar for flexural modes of vibration and is shown in Figure 2. From Figure 2, it is observed that the dimensionless wave number increases as non-dimensional frequency increases for all modes of vibration. Also it is observed that the dimensionless wave number increases as modes of vibration increases.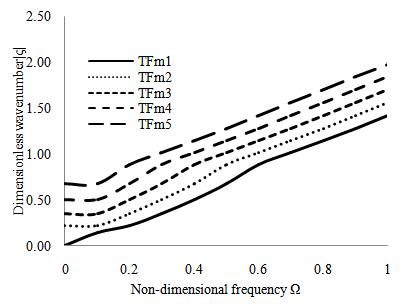 | Figure 2. Non-dimensional frequency Ω versus dimensionless wave number for a thermo-piezoelectric cylindrical bar for flexural modes of vibration |
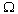 versus dimensionless wave number for a thermo-piezoelectric cylindrical bar immersed in fluid for longitudinal and flexural modes of vibration and are shown in Figures 3 and 4. From Figures 3 and 4, it is observed that the dimensionless wave number increases as non-dimensional frequency increases for increasing modes of vibration.
versus dimensionless wave number for a thermo-piezoelectric cylindrical bar immersed in fluid for longitudinal and flexural modes of vibration and are shown in Figures 3 and 4. From Figures 3 and 4, it is observed that the dimensionless wave number increases as non-dimensional frequency increases for increasing modes of vibration. 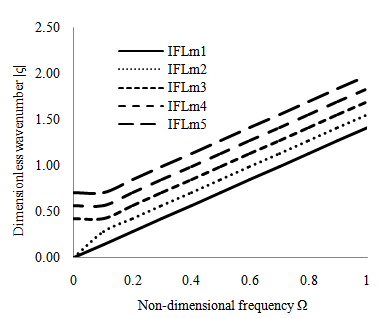 | Figure 3. Non-dimensional frequency Ω versus dimensionless wave number for a thermo-piezoelectric cylindrical bar immersed in fluid for longitudinal modes of vibration |
 | Figure 4. Non-dimensional frequency Ω versus dimensionless wave number for a thermo-piezoelectric cylindrical bar immersed in fluid for flexural modes of vibration |
 versus dimensionless wave number for a piezoelectric and thermo-piezoelectric cylindrical bar in space for longitudinal and flexural modes of vibration and are shown in Figures 5 and 6. From Figures 5 and 6, it is observed that dimensionless wave number of piezoelectric cylindrical bar is greater than the dimensionless wave number of thermo-piezoelectric cylindrical bar. Further it is observed that the dimensionless wave number of piezoelectric and thermo-piezoelectric cylindrical bar in space cross at some points and this cross over point represent the transfer of heat energy between the modes of vibration.
versus dimensionless wave number for a piezoelectric and thermo-piezoelectric cylindrical bar in space for longitudinal and flexural modes of vibration and are shown in Figures 5 and 6. From Figures 5 and 6, it is observed that dimensionless wave number of piezoelectric cylindrical bar is greater than the dimensionless wave number of thermo-piezoelectric cylindrical bar. Further it is observed that the dimensionless wave number of piezoelectric and thermo-piezoelectric cylindrical bar in space cross at some points and this cross over point represent the transfer of heat energy between the modes of vibration. 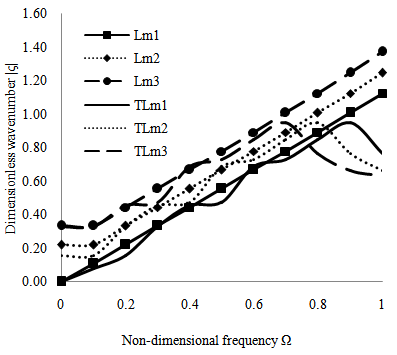 | Figure 5. Comparison between non-dimensional frequency Ω versus dimensionless wave number for a piezoelectric and thermo-piezoelectric cylindrical bar in space for longitudinal modes of vibration |
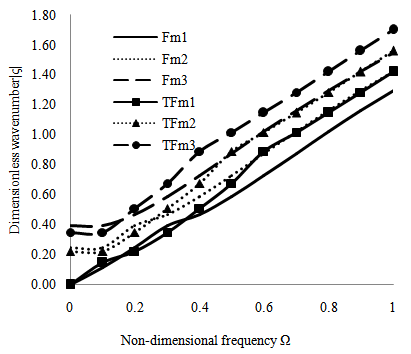 | Figure 6. Comparison between non-dimensional frequency Ω versus dimensionless wave number for a piezoelectric and thermo-piezoelectric cylindrical bar in space for flexural modes of vibration |
 versus dimensionless wave number for a thermo-piezoelectric cylindrical bar in space and immersed in fluid for longitudinal modes of vibration and is shown in Figure 7. From Figure 7, it is observed that the dimensionless wave number of thermo-piezoelectric cylindrical bar immersed in fluid is greater than the dimensionless wave number of thermo piezoelectric cylindrical bar in space for any modes of vibration. It is also observed that the dimensionless wave number of thermo piezoelectric cylindrical bar immersed in fluid linearly increases for all modes of vibration but the dimensionless wave number of thermo piezoelectric cylindrical bar in space increases and decreases simultaneously with respect to its non-dimensional frequency.
versus dimensionless wave number for a thermo-piezoelectric cylindrical bar in space and immersed in fluid for longitudinal modes of vibration and is shown in Figure 7. From Figure 7, it is observed that the dimensionless wave number of thermo-piezoelectric cylindrical bar immersed in fluid is greater than the dimensionless wave number of thermo piezoelectric cylindrical bar in space for any modes of vibration. It is also observed that the dimensionless wave number of thermo piezoelectric cylindrical bar immersed in fluid linearly increases for all modes of vibration but the dimensionless wave number of thermo piezoelectric cylindrical bar in space increases and decreases simultaneously with respect to its non-dimensional frequency.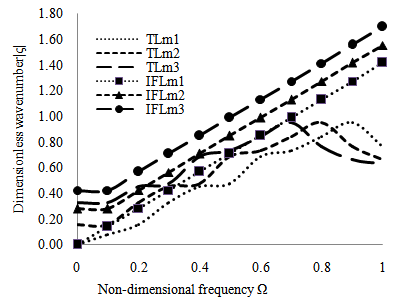 | Figure 7. Comparison between non-dimensional frequency Ω versus dimensionless wave number for a thermo-piezoelectric cylindrical bar in space and immersed in fluid for longitudinal modes of vibration |
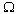 versus dimensionless wave number for a thermo-piezoelectric cylindrical bar in space and immersed in fluid for flexural modes of vibration and is shown in Figure 8.
versus dimensionless wave number for a thermo-piezoelectric cylindrical bar in space and immersed in fluid for flexural modes of vibration and is shown in Figure 8. 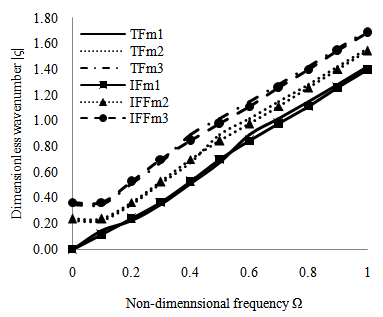 | Figure 8. Comparison between non-dimensional frequency Ω versus dimensionless wave number for a thermo-piezoelectric cylindrical bar in space and immersed in fluid for flexural modes of vibration |
8. Conclusions
- In this paper, wave propagation in a thermo-piezoelectric solid bar of circular cross-section immersed in fluid is discussed using three dimensional theory of thermo-piezoelectricity. The frequency equations are obtained for longitudinal and flexural modes of vibration. By choosing
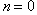 and
and 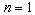 respectively, we can obtain the non-dimensional frequencies of longitudinal and flexural modes of vibration. Dispersion curves are drawn for non-dimensional frequency
respectively, we can obtain the non-dimensional frequencies of longitudinal and flexural modes of vibration. Dispersion curves are drawn for non-dimensional frequency  versus dimensionless wave number of thermo-piezoelectric cylindrical bar in space and immersed in fluid for both longitudinal and flexural modes of vibration. Also comparison graph is drawn for non-dimensional frequency versus dimensionless wave number between piezoelectric and thermo-piezoelectric cylindrical bar in space and between thermo-piezoelectric cylindrical bar in space and immersed in fluid respectively for both longitudinal and flexural modes of vibration. The same problem may be extended to study any kind of vibrational mode problem by choosing proper mathematical formulation.
versus dimensionless wave number of thermo-piezoelectric cylindrical bar in space and immersed in fluid for both longitudinal and flexural modes of vibration. Also comparison graph is drawn for non-dimensional frequency versus dimensionless wave number between piezoelectric and thermo-piezoelectric cylindrical bar in space and between thermo-piezoelectric cylindrical bar in space and immersed in fluid respectively for both longitudinal and flexural modes of vibration. The same problem may be extended to study any kind of vibrational mode problem by choosing proper mathematical formulation.Appendix A:
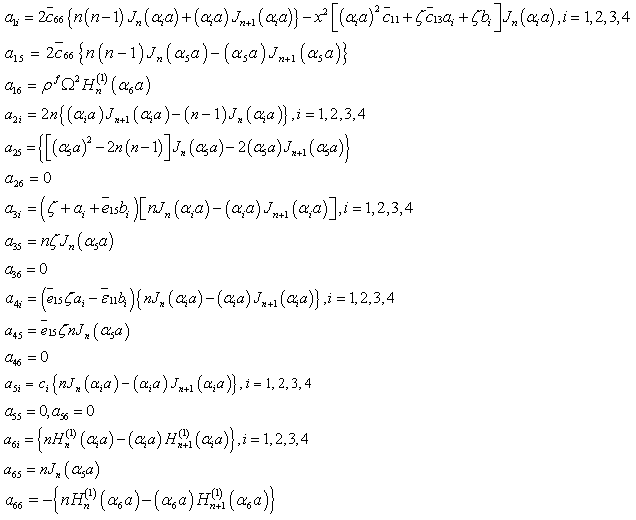
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML