-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Mechanics and Applications
p-ISSN: 2165-9281 e-ISSN: 2165-9303
2013; 3(5): 131-137
doi:10.5923/j.mechanics.20130305.04
Temperature Distribution along a Constant Cross Sectional Area Fin
Masoud Asadi1, Ramin Haghighi Khoshkho2
1Department of Mechanical Engineering Azad Islamic UniversityScience and Research branch, Tehran, Iran
2Department of Mechanical Engineering & Energy engineeringPower and Water University of Technology, Tehran, Iran
Correspondence to: Masoud Asadi, Department of Mechanical Engineering Azad Islamic UniversityScience and Research branch, Tehran, Iran.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Extended surfaces are extensively used in air-cooled automobile engines, air-conditioning systems, oil industries, computer processors, and other electronic devices. In various applications heat from the fins is dissipated by natural as well as forced convection and radiation. Fins are used as arrays in all the applications. Although many investigator have studied the heat transfer by natural and forced convection from extended surfaces, but the information about combined radiation and convection is sparse. In this paper, the interaction of thermal radiation with convection is numerically investigated, and an exact solution is presented for temperature distribution of fin of constant cross-sectional area. The influence of considering radiation on entropy generation and some heat transfer dimensionless numbers is also investigated. The results showed the temperature profile is uniform, and speed of transferring heat by Convection-Radiation increases along the fin. Also the accuracy of the solution is examined by a case study. The results showed good agreement.
Keywords: Radiation, Convection, Extended Surfaces, Temperature Distribution
Cite this paper: Masoud Asadi, Ramin Haghighi Khoshkho, Temperature Distribution along a Constant Cross Sectional Area Fin, International Journal of Mechanics and Applications, Vol. 3 No. 5, 2013, pp. 131-137. doi: 10.5923/j.mechanics.20130305.04.
Article Outline
1. Introduction
- If a surface , at a temperature above that of its surrounding, is located in stationary air at the some temperature as the surrounding then heat will be transferred from the surface to the air and surroundings. This transfer of heat will be a combination of naturally/ forced convection to the air and radiation to the surroundings. Radiation-Convection interaction problems are found in many situations, such as cooling of high-temperature components, furnace and combustion chamber design where heat transfer surfaces occurs by simultaneous radiation and convection, cooling of hypersonic and reentry vehicles, interactions of incident solar radiation with the earth’s surface to produce complex free-convection patterns and complicate the art of weather forecasting, convection cells and their effects on radiation from stars , andmarine environment studies for predicting free-convection patterns in oceans and lakes. The study of mixed convection combined with radiation in many industries is important. One of the this application is in the Microturbine applications, where the temperature of hot stream entering the heat exchanger is about
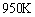 . If it be assumed that the type of the heat exchanger be Plate-Fin heat exchanger, radiation from fins is significant, and we cannot forbear it compared with forced convection. Although many researcher have studied about thermal performance of finned surface, but the problem of optimum design of radiation – convection fins of a given profile has remained virtually unexplored, and there is sparse information about temperature profile, heat transfer and entropy generation arising radiation-convection in finned surfaces.Harlap and McManus[1] studied on natural convection heat transfer from horizontal fin arrays. They found that heat transfer coefficients for vertical channels is more than horizontal channels. For rectangular fins on horizontal surfaces, Janes and Smith[2] suggested an optimum arrangement in order to have maximum heat transfer. Donvan and Roher[3] presented the fin temperature distribution, the local radiative heat transfer, the total convective heat transfer, and the effectiveness of the fins. Vandal Pol and Tierney[4] deduced that the vertical channel configuration shows the best performance for natural cooling. The effects of the fin thickness on natural convection arrays were investigated by Bar-Cohen[5]. The heat dissipation of parallel plates by natural convection was studied by Elenbaas[6]. Bilitzky et.al,[7] investigated the vertical base plate and horizontal fin arrays for the parameters such as fin length versus total heat dissipated if the fins on one side of sink and non-finned side of sink was adiabatic. Yuncu and Anbar[8] conducted experiments by different numbers of fins on a heated horizontal base plate of width 250 mm. increasing the numbers of fins, they found that for a given base-to-ambient temperature difference the rate of heat transfer due to the convection reaches a maximum at a particular fin spacing and fin height. Rammohan Rao and Venkateshan[9] studied the effects of fin height, fin spacing, fin array, base temperature, and fin emissivity on horizontal fin arrays. Firstly, the study of radiation effects on mixed convection was performed by G.Rod, M.Bertela and F.Santarelli[10]. They considered a two-dimensional channel flow with a participating irradiated fluid. Only absorption of radiation is thought to occur within the participating gray fluid. Combined radiation and laminar mixed convection in the thermal entrance region of horizontal isothermal rectangular channels was investigated by J.M.Huang and J.D.Lin[11]. Rao, and Naidu[24] studied the combined convection and radiation heat transfer form a fin array with a vertical base and horizontal fins. The mentioned literature review reveals that a more realistic numerical analysis of combined radiation and convection and its effects on the thermal performance of the heat exchanger in high temperature applications is required. Duan and Wang[12] analyzed temperature distribution and efficiency of convective straight fins with temperature - dependent thermal conductivity by a new modified decomposition method. Using this new method the temperature distribution and the efficiency of the fin can be expressed analytically as functions containing two fin parameters without any undetermined coefficients, which greatly facilitates parameter analysis. In a similar study, Acosta and Campo[13] conducted an analytical study on temperature distribution and efficiency for annular fins of uniform thickness. An inverse algorithm based on the conjugate gradient method and the discrepancy principle is applied by Lee and Chung[14] to estimate the unknown time-dependent base heat flux of a functionally graded fin from the knowledge of temperature measurements taken within the fin. Aziz et.al,[15] presented approximately solutions for the temperature distribution, fin efficiency, and optimum fin parameter for a constant areaLongitudinal fin with temperature dependent internal heat generation. Measurement of the temperature distribution ona circular plane fin is investigated by Bougriou and Bessaih[16]. They obtained the temperature distribution on this fins by an experimental approach, and making use of the infrared thermo graphy technique. Temperature distribution in a straight fin of rectangular profile with uniform and non-uniform internal heat generation characteristics and non-uniform heat transfer coefficients are derived analytically by Unal[17]. Yang and Chien[18] used the double decomposition method not only in analyzing the oscillating base temperature processes occurring in a convective rectangular fin with variable thermal conductivity, but also in determining the temperature distribution within the fin. Their results indicated that the series presented has high accuracy by comparing with those generated the complex combination method. An exact solution for thermal diffusion in a straight fin with varying exponential shape when the thermal conductivity and heat transfer coefficients are temperature dependent is investigated by Turkyilmazoglu[19]. Ranjan et.al,[20] carried out an experimental study on predicting unknown and possible combination parameters in a naturally convective porous fin subjected to a given temperature requirement. They estimated five critical parameters: porosity, solid, thermal conductivity, permeability, length and thickness of the fin by solving an inverse problem involving the simulated annealing.The objective of this study is to presentedan exact solution for temperature distribution arising convection-radiation along a constant cross sectional area fin. The effects of considering radiation in the terms of entropy generation, Biot number and Nusselt number are investigated, and compared with when there is just convection in the system.
. If it be assumed that the type of the heat exchanger be Plate-Fin heat exchanger, radiation from fins is significant, and we cannot forbear it compared with forced convection. Although many researcher have studied about thermal performance of finned surface, but the problem of optimum design of radiation – convection fins of a given profile has remained virtually unexplored, and there is sparse information about temperature profile, heat transfer and entropy generation arising radiation-convection in finned surfaces.Harlap and McManus[1] studied on natural convection heat transfer from horizontal fin arrays. They found that heat transfer coefficients for vertical channels is more than horizontal channels. For rectangular fins on horizontal surfaces, Janes and Smith[2] suggested an optimum arrangement in order to have maximum heat transfer. Donvan and Roher[3] presented the fin temperature distribution, the local radiative heat transfer, the total convective heat transfer, and the effectiveness of the fins. Vandal Pol and Tierney[4] deduced that the vertical channel configuration shows the best performance for natural cooling. The effects of the fin thickness on natural convection arrays were investigated by Bar-Cohen[5]. The heat dissipation of parallel plates by natural convection was studied by Elenbaas[6]. Bilitzky et.al,[7] investigated the vertical base plate and horizontal fin arrays for the parameters such as fin length versus total heat dissipated if the fins on one side of sink and non-finned side of sink was adiabatic. Yuncu and Anbar[8] conducted experiments by different numbers of fins on a heated horizontal base plate of width 250 mm. increasing the numbers of fins, they found that for a given base-to-ambient temperature difference the rate of heat transfer due to the convection reaches a maximum at a particular fin spacing and fin height. Rammohan Rao and Venkateshan[9] studied the effects of fin height, fin spacing, fin array, base temperature, and fin emissivity on horizontal fin arrays. Firstly, the study of radiation effects on mixed convection was performed by G.Rod, M.Bertela and F.Santarelli[10]. They considered a two-dimensional channel flow with a participating irradiated fluid. Only absorption of radiation is thought to occur within the participating gray fluid. Combined radiation and laminar mixed convection in the thermal entrance region of horizontal isothermal rectangular channels was investigated by J.M.Huang and J.D.Lin[11]. Rao, and Naidu[24] studied the combined convection and radiation heat transfer form a fin array with a vertical base and horizontal fins. The mentioned literature review reveals that a more realistic numerical analysis of combined radiation and convection and its effects on the thermal performance of the heat exchanger in high temperature applications is required. Duan and Wang[12] analyzed temperature distribution and efficiency of convective straight fins with temperature - dependent thermal conductivity by a new modified decomposition method. Using this new method the temperature distribution and the efficiency of the fin can be expressed analytically as functions containing two fin parameters without any undetermined coefficients, which greatly facilitates parameter analysis. In a similar study, Acosta and Campo[13] conducted an analytical study on temperature distribution and efficiency for annular fins of uniform thickness. An inverse algorithm based on the conjugate gradient method and the discrepancy principle is applied by Lee and Chung[14] to estimate the unknown time-dependent base heat flux of a functionally graded fin from the knowledge of temperature measurements taken within the fin. Aziz et.al,[15] presented approximately solutions for the temperature distribution, fin efficiency, and optimum fin parameter for a constant areaLongitudinal fin with temperature dependent internal heat generation. Measurement of the temperature distribution ona circular plane fin is investigated by Bougriou and Bessaih[16]. They obtained the temperature distribution on this fins by an experimental approach, and making use of the infrared thermo graphy technique. Temperature distribution in a straight fin of rectangular profile with uniform and non-uniform internal heat generation characteristics and non-uniform heat transfer coefficients are derived analytically by Unal[17]. Yang and Chien[18] used the double decomposition method not only in analyzing the oscillating base temperature processes occurring in a convective rectangular fin with variable thermal conductivity, but also in determining the temperature distribution within the fin. Their results indicated that the series presented has high accuracy by comparing with those generated the complex combination method. An exact solution for thermal diffusion in a straight fin with varying exponential shape when the thermal conductivity and heat transfer coefficients are temperature dependent is investigated by Turkyilmazoglu[19]. Ranjan et.al,[20] carried out an experimental study on predicting unknown and possible combination parameters in a naturally convective porous fin subjected to a given temperature requirement. They estimated five critical parameters: porosity, solid, thermal conductivity, permeability, length and thickness of the fin by solving an inverse problem involving the simulated annealing.The objective of this study is to presentedan exact solution for temperature distribution arising convection-radiation along a constant cross sectional area fin. The effects of considering radiation in the terms of entropy generation, Biot number and Nusselt number are investigated, and compared with when there is just convection in the system.2. Thermal Performance of Fin
2.1. Convection
- The rate of heat transfer from a surface at a temperature
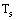 to the surrounding medium at
to the surrounding medium at 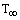 is given by Newton’s law of cooling as
is given by Newton’s law of cooling as 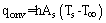 | (1) |
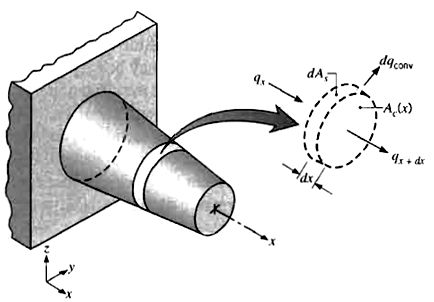 | Figure (1). Energy balance for an extended surface |
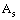 is the heat transfer surface area and
is the heat transfer surface area and 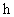 is the convection heat transfer coefficient. When the temperatures of
is the convection heat transfer coefficient. When the temperatures of 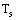 and
and 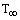 are fixed by design considerations, as is often the case, there are two ways to increase the rate of heat transfer : to increase the convection heat transfer coefficient or to increase the surface area. Also, it is possible to increase the temperature of surface, but there are many limitations in regard this way. Increasing h may require the installation of a pump or fan, or replacing the existing one with a larger one, but this approach may or may not be practical. Besides, it may not be adequate. The alternative is to increase the surface area by attaching to the surface called fins made of highly conductive materials such as aluminum. Finned surfaces are commonly used in practice to enhance heat transfer, and they often increase the rate of heat transfer from a surface severalfold. In analysis of fins, it is assumed that the steady operation with no heat generation in the fin as well as the thermal conductivity, k, of materials to remain constant. Also, it is assumed that the convection heat transfer coefficient , h , to be constant and uniform over the entire surface of the fin for convenience in the analysis. In general the convection heat transfer coefficient varies along the fin as well as its circumference, and its value at a point is a strong function of the fluid motion at that point. The value of h is usually much lover at the fin base than it is at the fin tip because the fluid is surrounding by solid surfaces near the base, which seriously disrupt its motion to the point of suffocating it, while the fluid near the fin tip has little contact with a solid surface and thus encounters little resistance to flow. Therefore, adding too many fins on a surface may actually decrease the overall heat transfer when the decrease in h offsets any gain resulting from the increase in the surface area. Under considerations, the energy balance on the volume element can be expressed as,
are fixed by design considerations, as is often the case, there are two ways to increase the rate of heat transfer : to increase the convection heat transfer coefficient or to increase the surface area. Also, it is possible to increase the temperature of surface, but there are many limitations in regard this way. Increasing h may require the installation of a pump or fan, or replacing the existing one with a larger one, but this approach may or may not be practical. Besides, it may not be adequate. The alternative is to increase the surface area by attaching to the surface called fins made of highly conductive materials such as aluminum. Finned surfaces are commonly used in practice to enhance heat transfer, and they often increase the rate of heat transfer from a surface severalfold. In analysis of fins, it is assumed that the steady operation with no heat generation in the fin as well as the thermal conductivity, k, of materials to remain constant. Also, it is assumed that the convection heat transfer coefficient , h , to be constant and uniform over the entire surface of the fin for convenience in the analysis. In general the convection heat transfer coefficient varies along the fin as well as its circumference, and its value at a point is a strong function of the fluid motion at that point. The value of h is usually much lover at the fin base than it is at the fin tip because the fluid is surrounding by solid surfaces near the base, which seriously disrupt its motion to the point of suffocating it, while the fluid near the fin tip has little contact with a solid surface and thus encounters little resistance to flow. Therefore, adding too many fins on a surface may actually decrease the overall heat transfer when the decrease in h offsets any gain resulting from the increase in the surface area. Under considerations, the energy balance on the volume element can be expressed as, | (1) |
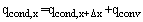 | (2) |
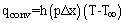 | (3) |
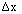 ,
,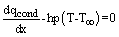 | (4) |
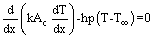 | (5) |
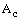 and the perimeter of a fin vary with x , which makes this differential equation difficult to solve. In special case of constant cross section and constant thermal conductivity, the equs. (5) will change to:
and the perimeter of a fin vary with x , which makes this differential equation difficult to solve. In special case of constant cross section and constant thermal conductivity, the equs. (5) will change to: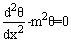 | (6) |
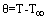 and
and 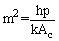 . Equation (6) is a linear, homogeneous, second-order differential equation with constant coefficients. Therefore, its general solution is:
. Equation (6) is a linear, homogeneous, second-order differential equation with constant coefficients. Therefore, its general solution is: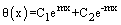 | (7) |
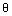 will approach zero. Finally, the temperature distribution for this case is:
will approach zero. Finally, the temperature distribution for this case is: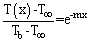 | (8) |
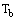 to
to 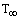 . For negligible heat loss from the fin tip, the temperature profile is :
. For negligible heat loss from the fin tip, the temperature profile is :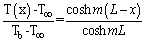 | (9) |
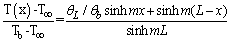 | (10) |
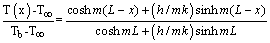 | (11) |
2.2. Combined Convection and Radiation
- The performance of the fin the figure of (2) depends on combined conduction, convection, and radiation. A gas at the temperature of
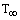 is flowing over the fin and removing heat by convection. The environment to which the fin radiates is also assumed to be at
is flowing over the fin and removing heat by convection. The environment to which the fin radiates is also assumed to be at 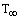 . The fin is non-gray with absorptivity
. The fin is non-gray with absorptivity 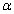 for radiation incident from the environment. From the control volume approach, an energy balance on a fin element of length dx is:
for radiation incident from the environment. From the control volume approach, an energy balance on a fin element of length dx is: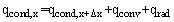 | (12) |
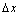 , this equation yields,
, this equation yields,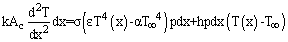 | (13) |
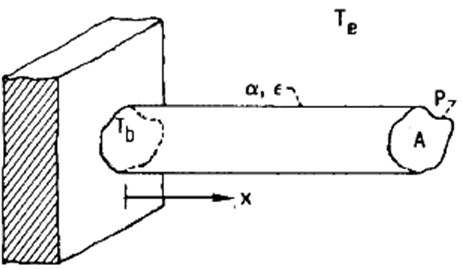 | Figure (2). Transferring energy by radiation and convection from a fin of constant cross-sectional area |
 to obtain,
to obtain,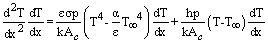 | (14) |
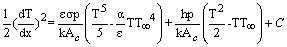 Where C is a constant of integration. The arbitrary constant can be evaluated at x=L, where
Where C is a constant of integration. The arbitrary constant can be evaluated at x=L, where 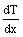 is set equal to zero and
is set equal to zero and 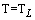 . So,
. So,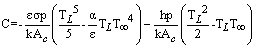 | (15) |
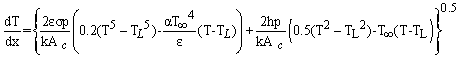 | (16) |
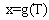 | (17) |
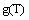 is a series, and can be expressed as,
is a series, and can be expressed as,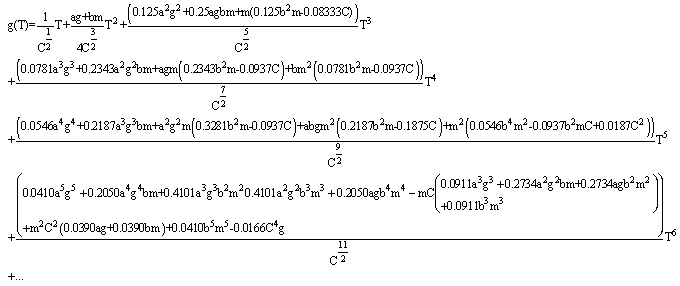 | (18) |
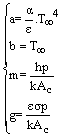 | (19) |
3. Validation
- R.Siegel and J.R.Howell[21] solved this problem with a simple conditions. They suggested an analytical solution for a long fin in free space
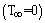 . Then for large x,
. Then for large x, 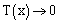 , and
, and 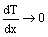 , and the constant C is zero. Solving for
, and the constant C is zero. Solving for 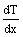 results in:
results in: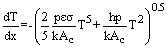 | (20) |
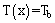 at
at 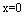 :
: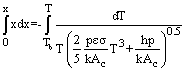 | (21) |
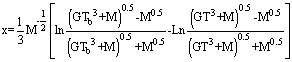 | (22) |
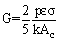 and
and 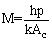 .To validate the equation of (18) a case study has been done. A very long rod 5mm in diameter has one end maintained at
.To validate the equation of (18) a case study has been done. A very long rod 5mm in diameter has one end maintained at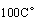 . The surface of rod is exposed to ambient air at
. The surface of rod is exposed to ambient air at 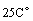 . The convection heat transfer coefficient is 100
. The convection heat transfer coefficient is 100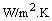 . The emissivity and absorptivity of copper are assumed that be 0.83 and 0.13 respectively.
. The emissivity and absorptivity of copper are assumed that be 0.83 and 0.13 respectively.4. Results and Discussion
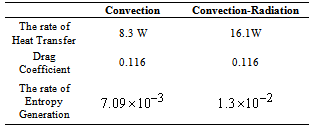
- Incropera[22] calculated the temperature distribution when there is only convection in the system. However, when there are both convection and radiation the results are as,
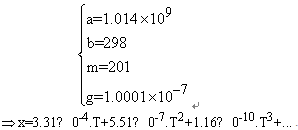 | (23) |
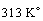 occur in x=183 mm, but the above equation denotes that when
occur in x=183 mm, but the above equation denotes that when 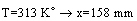 . The difference is due to several reasons. The main reason is that Incropera did not solve this problem based on the real conditions. He assumed that the rod is very long (
. The difference is due to several reasons. The main reason is that Incropera did not solve this problem based on the real conditions. He assumed that the rod is very long (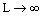 ). So, its solution is not precise and is an approximate method.The growth of fins on a solid wall increases the drag irreversibility of the wall-fluid configuration. Bejan[23] developed some correlations to calculate the rate of entropy generation in the extended surfaces. The entropy generation rate associated with fin fluid heat transfer is:
). So, its solution is not precise and is an approximate method.The growth of fins on a solid wall increases the drag irreversibility of the wall-fluid configuration. Bejan[23] developed some correlations to calculate the rate of entropy generation in the extended surfaces. The entropy generation rate associated with fin fluid heat transfer is: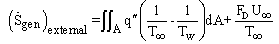 | (24) |
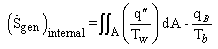 | (25) |
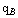 and
and 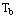 represent the base heat transfer and absolute temperature. Adding Equations of (24) and (25) side by side obtaining the entropy generation rate for a single fin is possible.
represent the base heat transfer and absolute temperature. Adding Equations of (24) and (25) side by side obtaining the entropy generation rate for a single fin is possible.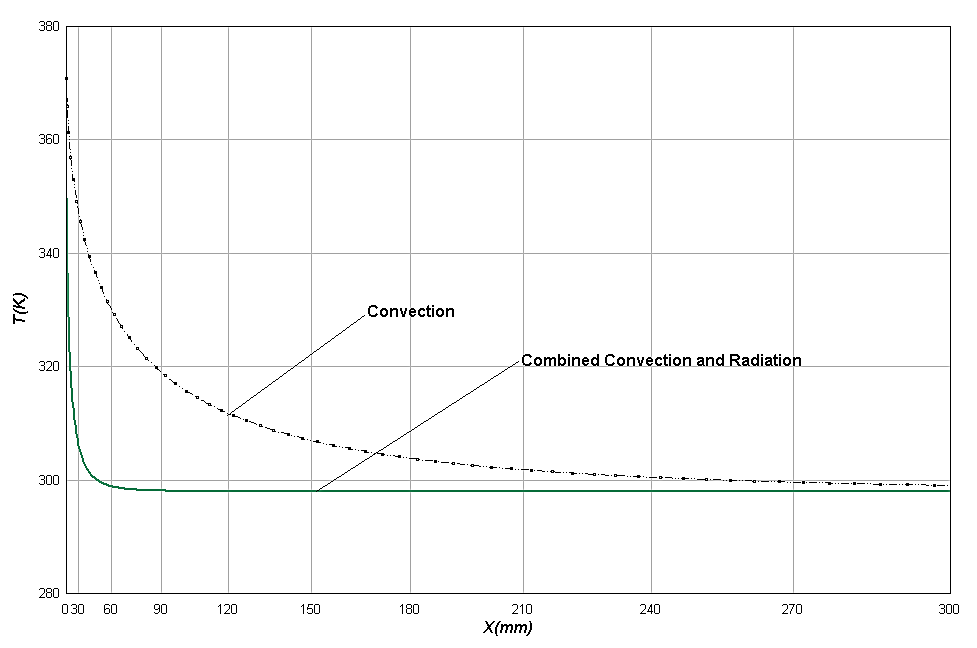 | Figure (3). Temperature distribution for Convection and Combined Convection-Radiation |
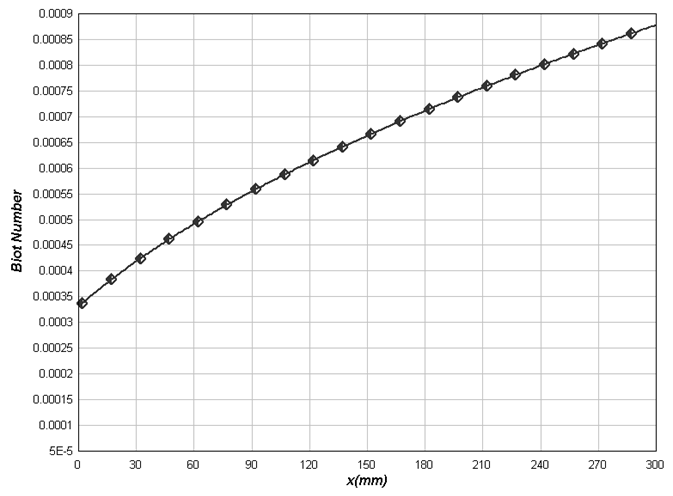 | Figure (4). Biot number versus length of the fin |
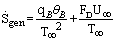 | (26) |
 is the base-stream temperature difference
is the base-stream temperature difference . Also, Drag coefficient for a pin fin is:
. Also, Drag coefficient for a pin fin is: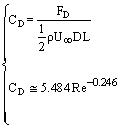 | (27) |
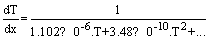 | (28) |
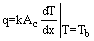 | (29) |
|
5. Conclusions
- In the air-to-air and air-to-liquid heat exchanger the heat transfer coefficient in the air side is small compared with the liquid side. One of the best solution to enhance heat transfer coefficient in the air side is using extended surfaces. In these cases temperature distribution is extremely affected by convection and in some situations by radiation. The results showed that when there is forced convection in the system we can ignore from the term of radiation in calculating heat transfer rate and temperature distribution. However, there are cases that radiation is important. For example, when there is natural convection or the temperature of hot fluid is so high. Generally when there is vacuum in the system there is natural convection. The other example for considering radiation is in microturbine application where the temperature of hot fluid is about 950 K. In this paper , an exact solution for temperature distribution is presented for uniform cross sectional area. The accuracy of the method presented is examined in the terms of entropy generation. The results showed high accuracy of the presented method. Also, the effects of considering radiation on the heat transfer dimensionless numbers are analyzed. The results dictate that the speed of transferring heat by radiation and convection increases in the length of the fin.
Nomenclature
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML