-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Mechanics and Applications
p-ISSN: 2165-9281 e-ISSN: 2165-9303
2013; 3(5): 105-116
doi:10.5923/j.mechanics.20130305.01
Vertical Baffles Height Effect on Liquid Sloshing in an Accelerating Rectangular Tank
Abdallah Bouabidi, Zied Driss, Mohamed Salah Abid
National Engineering School of Sfax (ENIS), Laboratory of Electro-Mechanic Systems (LASEM), University of Sfax, B.P. 1173, km 3.5 Road Soukra, 3038, Sfax, Tunisia
Correspondence to: Zied Driss, National Engineering School of Sfax (ENIS), Laboratory of Electro-Mechanic Systems (LASEM), University of Sfax, B.P. 1173, km 3.5 Road Soukra, 3038, Sfax, Tunisia.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Sloshing is a phenomenon which still needs considerable understanding in its behaviour related to various engineering problems and is a composition of highly nonlinear waves that may lead to structural damage of the side walls of the container and may destabilize the ship. The aim of this study is to numerically predict the damping effect of baffles on sloshing in tanks partially filled with liquid. The effectiveness and the effect of mounting a baffle vertically just at the free surface on the attenuation of sloshing waves and reduction of the overturning moment were underlined. Commercial software code FLUENT is used as a computational platform in this study. Based on the Navier-Stokes equations for viscous, incompressible fluid and Volume of fluid (VOF) method, a two dimensional numerical wave tank is established.
Keywords: VOF, Sloshing, Turbulent Flow, Baffles, Tank
Cite this paper: Abdallah Bouabidi, Zied Driss, Mohamed Salah Abid, Vertical Baffles Height Effect on Liquid Sloshing in an Accelerating Rectangular Tank, International Journal of Mechanics and Applications, Vol. 3 No. 5, 2013, pp. 105-116. doi: 10.5923/j.mechanics.20130305.01.
Article Outline
1. Introduction
- Liquid sloshing in a moving tank constitutes major components in a number of dynamical systems such as aerospace vehicles, road tankers, liquefied natural gas carriers, elevated water towers and petroleum cylindrical tanks. Fluid motion in partially filled tanks can cause large structural loads if the period of tank motion is close to the natural period of fluid inside the tank. The amplitude of the slosh, in general, depends on amplitude and frequency of the tank motion, liquid-fill depth, liquid properties and tank geometry. These parameters have direct effects on the dynamic stability and performance of moving tanks. The baffle inside a tank has been investigated by many researchers and the several recent studies on the effect of baffle on liquid sloshing are summarized as follows. For example Ibrahim et al.[1] analysed the two-dimensional nonlinear sloshing of an incompressible fluid with irrotational flow in a rectangular tank. Sakai et al.[2] investigated the sloshing behavior of floating-roofed oil storage tanks through theoretical analysis and model testing. Kim[3] analysed the sloshing flows with impact load in the two- and three-dimensional containers based on a finite difference method. Mikelis and Journee[4] designed a prototype of the cargo tanks used to transport liquid cargo in ships. They have studied that the integration of pressures around the tank walls yields to overall forces and moments that are transmitted by the liquids onto the tank structure and consequently on the ship. Chen et al.[5] developed finite-difference method to analyse sloshing in tanks. Nakayama et al.[6] tackled the problem of sloshing by the boundary element method. They took into consideration the damping effect due to the fluid viscosity by adding an artifice known as the Rayleigh damping term to the condition at the free surface. The control of the sloshing behaviour with baffles is also a subject of interest in the recent years, because of the complexity and highly nonlinear nature of the problem. Some researches carried out the experimental and numerical studies and pointed out the above mentioned characteristics[7-9]. Cho et al.[10] published the results of a resonance analysis of a 2D tank provided with horizontal baffles. With respect to the results of this analysis, it was concluded that the damping effect due to the use of horizontal baffles is significant. Pal and Bhattacharyya[11] carried out the numerical and experimental studies of liquid sloshing for 2D problem. The resulting slosh heights for various excitation frequencies and amplitudes are compared with the data obtained numerically. It was concluded that the little variations in the data are due to the ineptness of the experimental setup and the input parameters. Panigrahy et al.[12] showed experimentally that baffles in a tank decrease the sloshing effect considerably because sharp edged baffles create turbulence in the flow field by dissipating the excess kinetic energy to the walls. Xue and Lin[13] developed a three-dimensional (3-D) numerical model to study viscous liquid sloshing in a tank with internal baffles of different shapes and arrangements. Belakroum et al.[14] predicted the damping effect of baffles on sloshing in tanks partially filled with liquid. Chih-Hua et al.[15] used a time-independent finite difference scheme with fictitious cell technique to study viscous fluid sloshing in 2D tanks with baffles. Hakan[16] presented a numerical algorithm based on the volume of fluid (VOF) technique to study the non linear behaviour of liquid sloshing. According to these studies it appears that the sloshing in tanks is very interesting. For this, the effects of the vertical baffle height on liquid sloshing in an accelerating rectangular tank have been investigated.
2. Geometrical Arrangement
- In this paper, a rectangular tank is considered. The geometry is given by the length equal to b=2 m and the height equal to H=3 m, as shown in Figure 1. The topless tank is partially filled with a fluid height equal to h=2.5 m. The height of the baffle hb is established with the ratio of baffle height to the initial liquid height varying from hb/h=0.2 to hb/h=1. The used fluid is the water where the density ρ=1000 kg.m-3. The top surface of the fluid is in a state of free surface. The tank is accelerated horizontally with γ=15 m.s-2 along a line parallel to two of the walls.
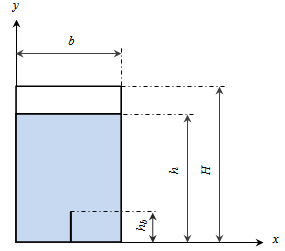 | Figure 1. Geometrical arrangement |
3. Numerical Model
- The commercial CFD code "Fluent" has been used to present the local flow characteristics in the tank. The Navier-Stokes equations in conjunction with the standard k-ε turbulence model were solved using a finite volume discretization method[17-21].
3.1. Mathematical Model
- Fluid motion within the fluid is described by the NavierStokes equations. This is a set of nonlinear three dimensional partial differential equations.The first equation describes the conservation of mass:
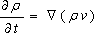 | (1) |
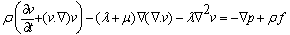 | (2) |
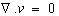 | (3) |
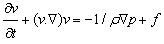 | (4) |
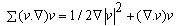 | (5) |
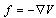 | (6) |
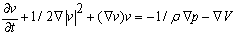 | (7) |
3.2. Boundary Conditions
- The fluid boundaries in the problem considered are the container walls, bottom and the free surface of the fluid. On the container walls and bottom, the boundary condition is that the velocity of the flow at the wall is zero in the normal direction of the wall.
4. Numerical Results
- In this section, we examine numerically how the height of the baffle relative to the initial liquid height affects the liquid sloshing phenomenon when the vertical blade baffle is located at the center of the bottom wall of the tank which is accelerated horizontally with γ= 15m.s-2 along a line parallel to two of the walls. Therefore, the main aim of this section is to determine the behavior of the free surface elevation, the velocity fields, the static pressure, the vorticity, the turbulent kinetic energy, the turbulent dissipation rate, and the turbulent viscosity depending on the baffle height. The commercial CFD package "Fluent" is employed for all numerical predictions.
4.1. Free Surface Deformation
- Figure 2 presents free surface deformation for different baffle heights equal to hb/h=0, hb/h=0.2, hb/h=0.4, hb/h=0.6, hb/h=0.8 and hb/h=1. When the tank has the baffle with the heights of hb/h=0.2 and hb/h=0.4 among the baffle heights considered in this study, the pattern of liquid sloshing is similar to the case of the unbaffled tank. As the baffle height increases steadily, the lateral motion of the liquid becomes weaker owing to the augmentation of the blockage effect of the baffle on the liquid convection especially in the region under the baffle. Successively, the free surface behavior becomes stable and the inertial forces are not enough to propel the liquid along the side wall to reach the top wall of the tank. This can be clarified by comparing between the unbaffled tank and the baffled tank with hb/h=1.
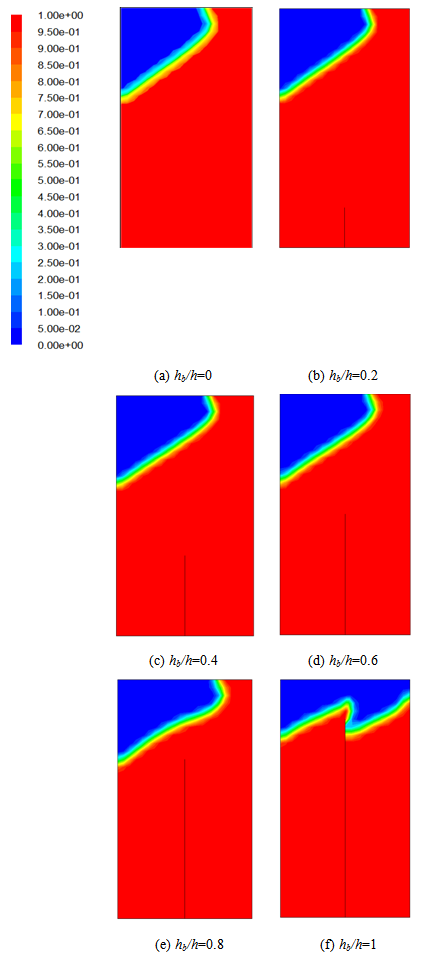 | Figure 2. Free surface deformation |
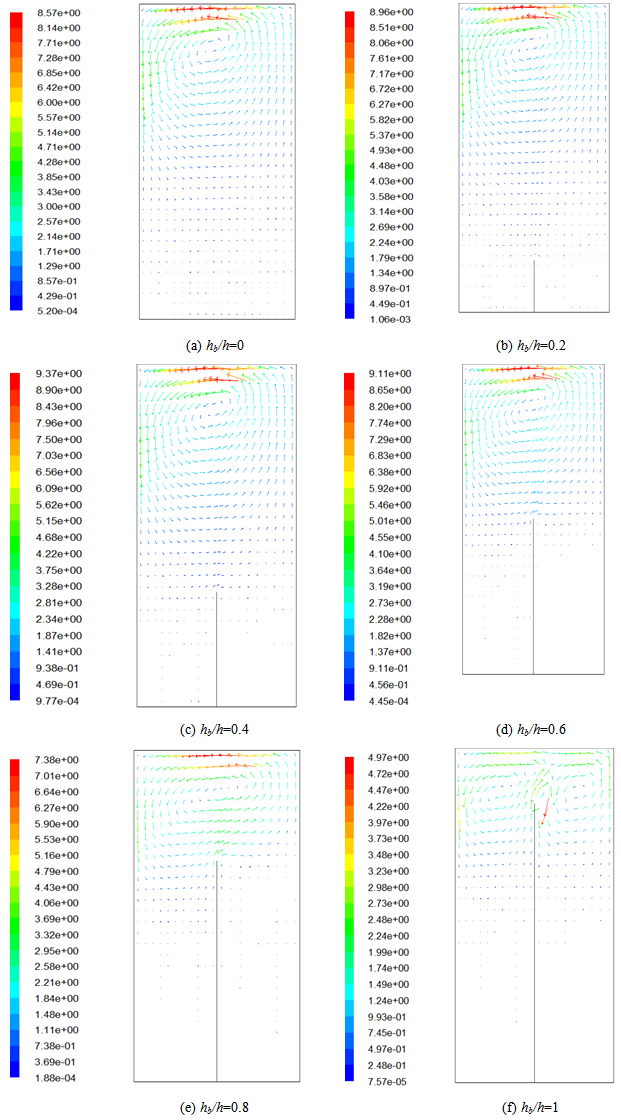
4.2. Velocity Fields
- Figure 3 presents the velocity fields for different baffle heights equal to hb/h=0, hb/h=0.2, hb/h=0.4, hb/h=0.6, hb/h=0.8 and hb/h=1. According to these results, when the considered tank has the baffle with the heights of hb/h=0.2, hb/h=0.4 and hb/h=0.6, we observe an accelerate movement of the flow compared with the case of the unbaffled tank. When the tank has the baffle with the heights of hb/h=0.8 and hb/h=1, a decelerate movement has been observed. The maximum velocity value is obtained for the baffled tank with the height of hb/h=0.4. However the minimum velocity value is obtained for the baffled tank with the height of hb/h=1. A recirculation zone appears in the top of the tank. The extension decreases with the increase of the baffle height. The largest recirculation zone is founded without baffle. However, for the baffle height hb/h=1 it divided in two small recirculation zones.
4.3. Static Pressure
- The pressure distribution caused by liquid sloshing at different probes are shown in figure 4 in which the six different baffle heights considered in this study are equal to hb/h=0, hb/h=0.2, hb/h=0.4, hb/h=0.6, hb/h=0.8 and hb/h=1. According to these results, when the tank has the baffle with the heights of hb/h=0.2, hb/h=0.4 and hb/h=0.6 and hb/h=0.8, the compression zones are located at the down right corner of the tank. When the tank has the baffle with the height of hb/h=1, the compression zone are located in the down right corner of the tank and in the baffle down. As the baffle height increases steadily, the value of the static pressure near to the baffle increases.
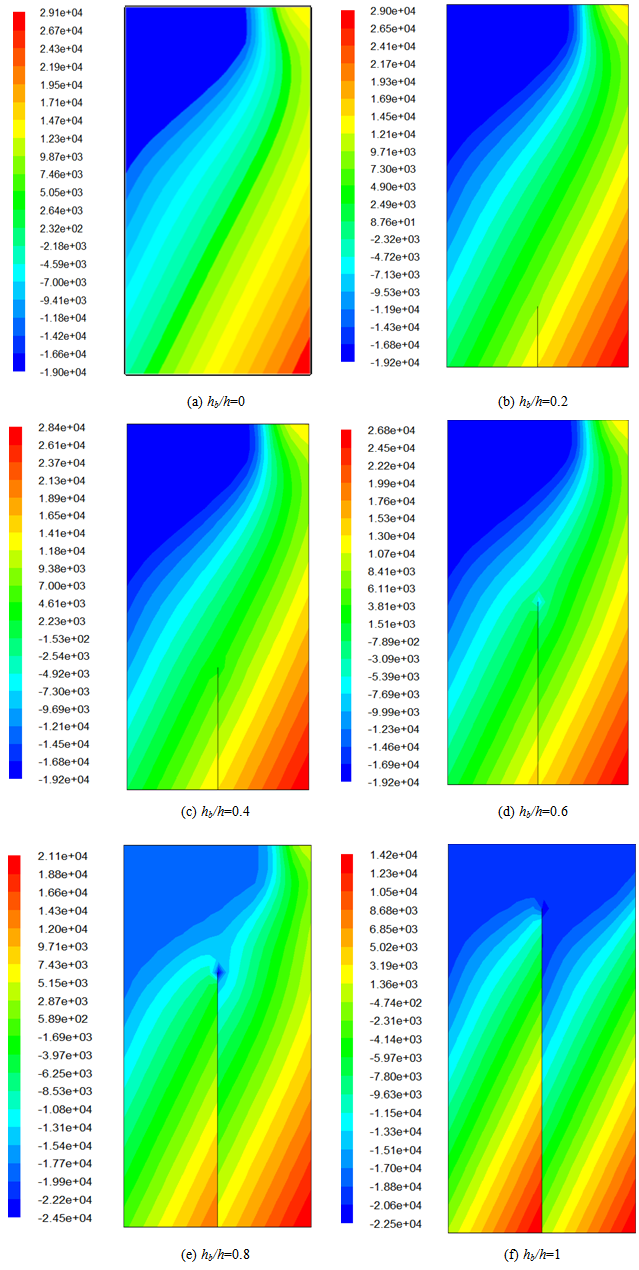 | Figure 4. Distribution of static pressure |
4.4. Vorticity
- The distribution of the vorticity caused by liquid sloshing at different probes are shown in figure 5 in which the six different baffle heights considered in this study are equal to hb/h=0, hb/h=0.2, hb/h=0.4, hb/h=0.6, hb/h=0.8 and hb/h=1. For the unbaffled tank, the highest value of vorticity is located at the free surface. However, with the different considered baffle heights, the highest value of vorticity is located at the free surface and above of the baffle. For the baffle heights equal to hb/h=0.2, hb/h=0.4 and hb/h=0.6, the vorticity value increases with the increase of the baffle height. The maximum vorticity value has been observed for the baffled tank with the height of hb/h=0.6 and it is located in the baffle top. However the minimum value has been observed for the baffled tank with the height of hb/h=1 and for the unbaffled tank.
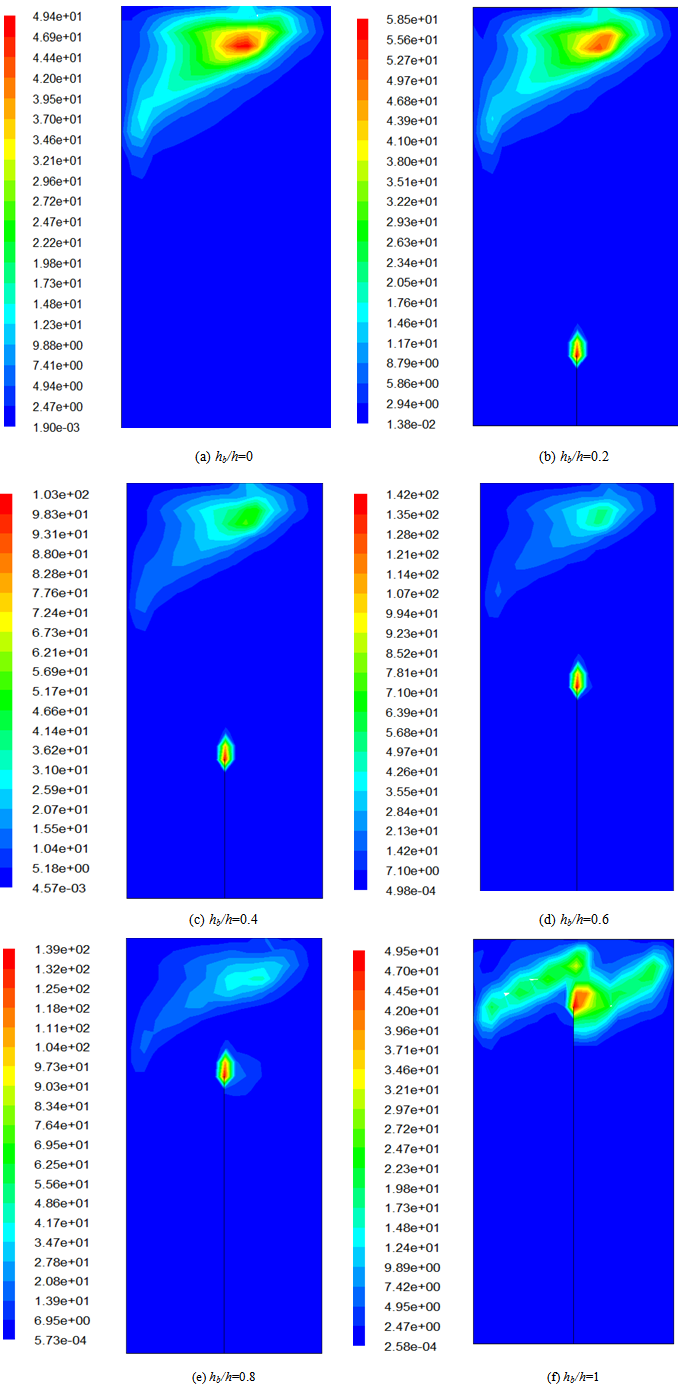 | Figure 5. Distribution of vorticity |
4.5. Turbulent Kinetic Energy
- The distribution of the turbulent kinetic energy caused by liquid sloshing at different probes are shown in figure 6 in which the six different baffle heights considered in this study are equal to hb/h=0, hb/h=0.2, hb/h=0.4, hb/h=0.6, hb/h=0.8 and hb/h=1. According to these results, the turbulent kinetic energy is maximum for the baffled tank with the height of hb/h=0.4 and it is minimum for the baffled tank with the height of hb/h=1. When the tank has the baffle with the height of hb/h=0.2, hb/h=0.4 and hb/h=0.6 among the baffle heights considered in this study, the turbulent kinetic energy is greater than the unbaffled tank. However for the baffle height equal to hb/h=0.8 and hb/h=1, the turbulent kinetic energy is lower than the unbaffled tank.
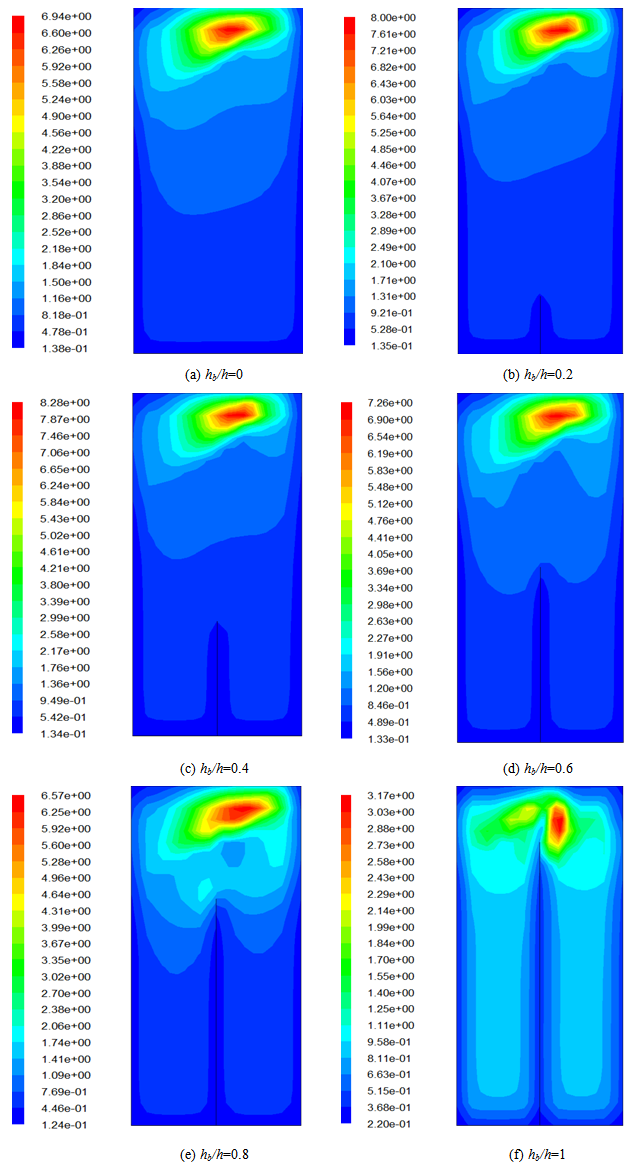 | Figure 6. Distribution of the turbulent kinetic energy |
4.6. Dissipation Rate of the Turbulent Kinetic Energy
- The distribution of the dissipation rate of the turbulent kinetic energy caused by liquid sloshing at different probes are shown in figure 7 in which the six different baffle heights considered in this study are equal to hb/h=0, hb/h=0.2, hb/h=0.4, hb/h=0.6, hb/h=0.8 and hb/h=1. According to these results, the dissipation rate of the turbulent kinetic energy is maximum for the baffled tank with the height hb/h=0.4 and it is minimum for the baffled tank with the height of hb/h=1. When the tank has the baffle height equal to hb/h=0.2, hb/h=0.4 and hb/h=0.6, the turbulent dissipation rate is greater than the unbaffled tank. However, with the baffle height equal to hb/h=0.8 and hb/h=1, the turbulent dissipation rate is lower than the unbaffled tank.
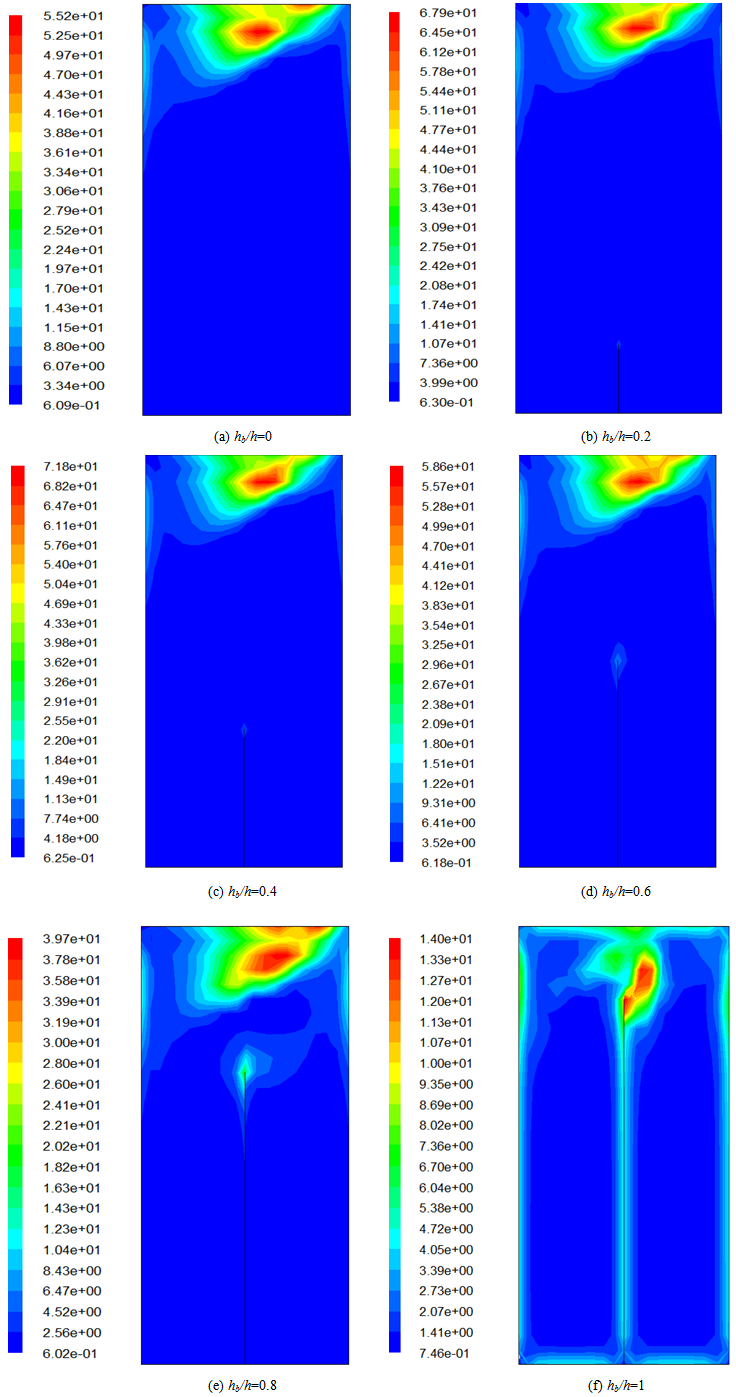 | Figure 7. Distribution of the turbulent dissipation rate |
4.7. Turbulent Viscosity
- The distribution of the turbulent viscosity caused by liquid sloshing at different probes are shown in figure 8 in which the six different baffle heights considered in this study are equal to hb/h=0, hb/h=0.2, hb/h=0.4, hb/h=0.6, hb/h=0.8 and hb/h=1. According to these results, the wake characteristic of the maximum values of the turbulent viscosity appears on the hall volume of water. However, the wake characteristic of the minimum values appears on the areas close to the wall and the baffle.
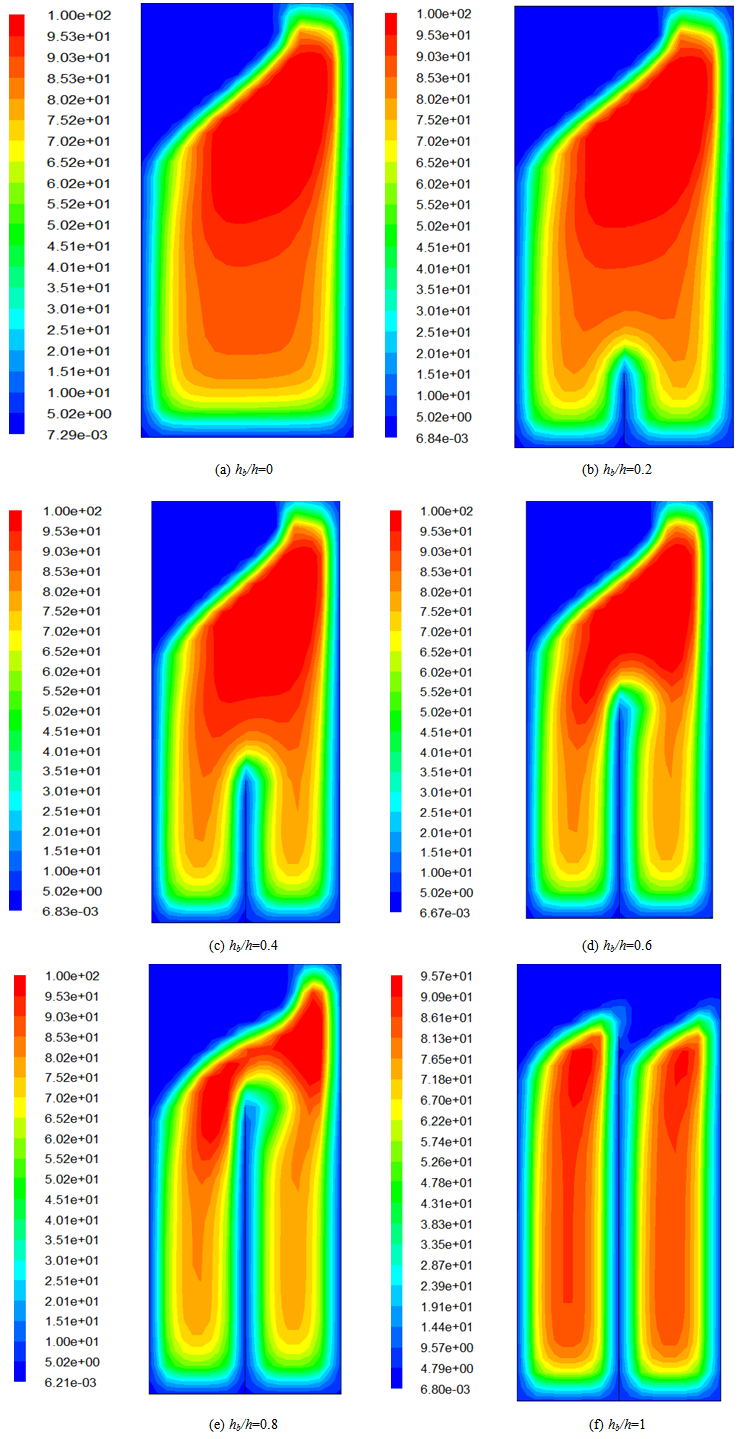 | Figure 8. Distribution of turbulent viscosity |
5. Conclusions
- In this paper, we have studied the effect of a vertical blade baffle on liquid sloshing in a two dimensional rectangular tank by solving two dimensional unsteady incompressible Navier-Stokes equations with the turbulence closure model of the standard k-ε turbulence model. The volume of fluid method has been used to simulate two-phase flow in laterally moving rectangular unbaffled and baffled tanks. According to this study, we confirm that the baffle height has a direct effect on the hydrodynamic results. In fact, when the baffle height increases, the liquid sloshing becomes more suppressed due to the augmentation of the blockage effect of the baffle, which results in additional viscosity and energy dissipation, also known as hydrodynamic damp.In the future, we propose to develop a three dimension simulation to study a new tank designs.

 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML