| [1] | E. Mathieu. Memoire sure le Mouvement Vibratiore d’une Membrane de Forme Elliptique, J. Math. 13, 137-203, 1868. |
| [2] | A. Nayfeh, D. T. Mook. Nonlinear Oscillations. Wiley, New York, 1979. |
| [3] | R. H. Rand. Lecture notes on nonlinear vibrations (version 53). Available fromhttp//audiophile.tam.cornell.edu/randdocs/; 2012. |
| [4] | J. J. Stoker. Nonlinear vibrations in mechanical and electrical systems. New York; 1950. |
| [5] | M. E. Bauer. Existence and stability of patterns arising from square wave forcing of the damped Mathieu equation. Senior honors Thesis, Department of Mathematics, Duke University, 2008. Available from http//www.stanford.edu/̴mebauer/pdf/pruv_thesis.pdf. |
| [6] | T. Insperger, G. Stepan. Stability of the damped Mathieu equation with time delay. Journal of Dynamic Systems, Measurement and control 125, 166-171, 2003. |
| [7] | T. M. Morrison, R. H. Rand. 2:1 Resonance in the delayed nonlinear Mathieu equation. Nonlinear Dyn 50, 341-352, 2007. |
| [8] | D.V. Ramani, R. H. Rand, W. L. Keith. A bifurcation analysis of the quadratically damped Mathieu equation and its applications to the dynamics of Submarine Towed-Array Lifting Devices. Available fromhttp//audiophile.tam.cornell.edu/randpdf/udt01.pdf. |
| [9] | R. H. Rand, S. M. Sah, M. K. Suchorsky. Fractional Mathieu equation. Commun Nonlinear Sci Numer Simulat 15, 3254-3262, 2010. |
| [10] | A. Ebaid, D. M. M. Elsayeed, M. D. Aljoufi. Fractional Calculus Model for Damped Mathieu Equation: Approximate Analytical Solution. J. Appl. Math. Sci. 6(82), 4075-4080, 2012. |
| [11] | H. M. Srivasta, R.K. Saxena. Operators of fractional integration and their applications, Appl. Math. Comput., 118, 1-52, 2001. |
| [12] | R. L. Bagley, P. J. Torvik. A theoretical basis for the application of fractional calculus to viscoelasticity, J. Rheol., 27, 201-210, 1983. |
| [13] | R. Hilfer (ED). Applications of Fractional Calculus in Physics, Applications of Fractional Calculus in Physics, 2000. |
| [14] | I. Podlubny. Fractional Differential Equations, Academic press, San Diego, California, 1999. |
| [15] | B. Ross. A brief history and exposition of the fundamental theory of fractional calculus, In: Fractional calculus and its applications. Springer lecture notes in mathematics, 57, 1-36, 1975. |
| [16] | P. Pue-on and N. Viriyapong. Modified Adomian Decomposition Method for Solving Particular Third-Order Ordinary Differential Equations. Applied Mathematical Sciences 6(30), 1463-1469, 2012. |
| [17] | R. Montazeri. A Concrete Application of Adomian Decomposition Method. Int. J. Contemp. Math. Sciences 7(24), 1185-1192, 2012. |
| [18] | E. Celik, M. Bayram and T. Yeloglu. Solution of Differential-Algebraic Equations(DAEs) by Adomian Decomposition Method. International Journal Pure & Applied Mathematical Sciences 3(1) , 93-100, 2006. |
| [19] | T. R. Ramesh Rao. The use of Adomian Decomposition Method for Solving Generalised Riccati Differential Equations. Proc. 6th IMT-GT Conference on Mathematics, Statistics and its Applications (ICMSA2010) Universiti Tunku Abdul Rahman, Kuala Lumpur, Malaysia 2010. |
| [20] | S. Somali and G. Gokemen. Adomian Decomposition Method for Nonlinear Sturm-Liouville Problems. Surveys in Mathematics and its Application 2, 11-20, 2007. |
| [21] | H. Fatoorehchi and H. Abolghasemi. Adomian Decomposition Method to Study Mass Transfer from a Horizontal Flat Plate subject to Laminar Fluid Flow. Advances in Natural and Applied Sciences 5(1), 26-33, 2011. |
| [22] | Q. Yu, F. Liu, V. Anh and I. Turne. Solving linear and non-linear space-time fractional reaction-diffusion equations by the Adomian Decomposition Method. International Journal for Numerical Methods in engineering 78, 138-158, 2008. |
| [23] | S. Pamuk. An application for linear and nonlinear equations by Adomian Decomposition Method. Applied Mathematics and Computation 163, 89-96, 2005. |
| [24] | A. M. Wazwaz and A. Gorguis. An analytic study of Fisher’s equation by Adomian Decomposition Method. Applied Mathematics and Computation 154, 609-620, 2004. |
| [25] | E. A. Ibijola, B. J. Adegboyegun, O. Y. Halid. On Adomian Decomposition Method (ADM) for Numerical Solution of Ordinary Differential Equations. Advances in Natural and Applied Sciences 2(3), 165-169, 2008. |
| [26] | G. Adomian. Solutions of nonlinear PDE. Applied Mathematical Letters 11(13), 121-123, 1998. |
| [27] | G. Adomian. Solving Frontier Problems of Physics: The Decomposition Method. Kluwer Academic Publishers, Boston 1994. |
| [28] | M. R. Roussel. Delay-differential equations. Available from http://people.uleth.ca/~roussel/nld/delay.pdf. |
| [29] | C. E. Falbo. Some Elementary Meyhods for Solving Functional Differential Equations. Available from http://www.mathfile.net/hicstat_FDE.pdf. |
| [30] | T. K. Nagy. Stability analysis of delay-differential equations by the method of steps and inverse Laplace transform, Differential Equations and Dynamical Systems 17(1&2), 185-200, 2009. |
| [31] | A. H. M. Abdelrazec. Adomian Decomposition Method: Convergence Analysis and Numerical Approximations. M.Sc Thesis McMaster University, 2008. Available from http://dmpeli.math.mcmaster.ca/PaperBank/ThesisAhmed.pdf. |
| [32] | T. Mavoungou and Y. Cherruault. convergence of adomian’s method and applications to nonlinear partial differential equations, kybernetes 21(6), 13-25, 1992. |

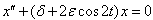
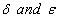 , it was noted in[3, 4] that either all solutions of Eq. (1) are bounded (stable) or an unbounded (unstable) solution exists. The existence of stable and unstable solutions to the un-damped Eq. (1) and damped Eq. (2) Mathieu’s equation is attributed to the parametric forcing introduced into the system[5]. Reference[5] investigated the nature and stability of patterns arising from parametric square-wave forcing of an inviscid fluid layer of infinite depth. In[5], the linear damped Mathieu equation which was derived from the nonlinear PDE’s of the Zhang-Vinals model of a fluid surface under small perturbations, was employed. Reference[6] investigated the delayed and damped Mathieu’s equation defined by Eq. (3) and determined stability chart connecting the Strut-Ince chart of the damped Mathieu equation (2) and the Hsu-Bhah-Vysnegradskii chart of the autonomous second order delay differential equation. The dynamics of the undamped and delayed Mathieu equation with a cubic nonlinearity Eq. (6) was also investigated by[7] using the method of averaging
, it was noted in[3, 4] that either all solutions of Eq. (1) are bounded (stable) or an unbounded (unstable) solution exists. The existence of stable and unstable solutions to the un-damped Eq. (1) and damped Eq. (2) Mathieu’s equation is attributed to the parametric forcing introduced into the system[5]. Reference[5] investigated the nature and stability of patterns arising from parametric square-wave forcing of an inviscid fluid layer of infinite depth. In[5], the linear damped Mathieu equation which was derived from the nonlinear PDE’s of the Zhang-Vinals model of a fluid surface under small perturbations, was employed. Reference[6] investigated the delayed and damped Mathieu’s equation defined by Eq. (3) and determined stability chart connecting the Strut-Ince chart of the damped Mathieu equation (2) and the Hsu-Bhah-Vysnegradskii chart of the autonomous second order delay differential equation. The dynamics of the undamped and delayed Mathieu equation with a cubic nonlinearity Eq. (6) was also investigated by[7] using the method of averaging 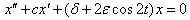
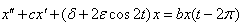
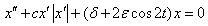
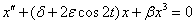
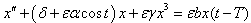
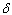 is the transient curve,
is the transient curve, 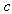 is the damping coefficient,
is the damping coefficient, 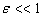 is a small parameter and
is a small parameter and 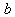 is the delay coefficient. The quadratically damped Mathieu equation defined by (4), happens to be satisfied by the dynamics of towed array lifting devices (LFDs) as shown in[8]. This LFDs help to maintain the position of a tow line being dragged behind. In[8], the dynamical features of the system (4) was exploited to obtain a control strategy for maintaining the LFD in the desired state. A detailed analysis of Mathieu’s equation especially that of stability can be found in[3]. Furthermore, Mathieu’s equation has wide applications in Boundary Value Problems (BVPs) and recently it has been found out that Mathieu’s equation is practically applied in the following areas: vibrations in an elliptic drum, the inverted pendulum, the radio frequency quadrupole, frequency modulation, stability of a floating body, alternating gradient focusing, the Paul trap for charged particles, and the mirror trap for neutral particles. In all these extensive studies, we note that the fractional aspect of Mathieu’s equation is not left out, see[9,10].
is the delay coefficient. The quadratically damped Mathieu equation defined by (4), happens to be satisfied by the dynamics of towed array lifting devices (LFDs) as shown in[8]. This LFDs help to maintain the position of a tow line being dragged behind. In[8], the dynamical features of the system (4) was exploited to obtain a control strategy for maintaining the LFD in the desired state. A detailed analysis of Mathieu’s equation especially that of stability can be found in[3]. Furthermore, Mathieu’s equation has wide applications in Boundary Value Problems (BVPs) and recently it has been found out that Mathieu’s equation is practically applied in the following areas: vibrations in an elliptic drum, the inverted pendulum, the radio frequency quadrupole, frequency modulation, stability of a floating body, alternating gradient focusing, the Paul trap for charged particles, and the mirror trap for neutral particles. In all these extensive studies, we note that the fractional aspect of Mathieu’s equation is not left out, see[9,10]. 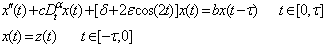
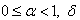 is the transient curve conventionally regarded as the frequency of the system squared,
is the transient curve conventionally regarded as the frequency of the system squared, 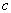 is the damping coefficient,
is the damping coefficient, 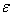 is the amplitude of the parametric resonance,
is the amplitude of the parametric resonance, 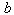 is the delay amplitude and
is the delay amplitude and 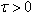 is the time delay, and
is the time delay, and 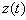 is a given function. We note that when
is a given function. We note that when 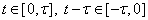 , thus
, thus 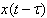 may be taken as
may be taken as 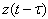 on
on 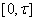 .Then for the interval
.Then for the interval 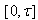 , Eq. (7) becomes
, Eq. (7) becomes 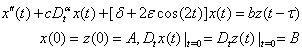
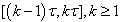 , may be solved by successively replacing the R. H. S of Eq. (8) with the solution obtained from the previous
, may be solved by successively replacing the R. H. S of Eq. (8) with the solution obtained from the previous  equation. Eq. (8) is for the case
equation. Eq. (8) is for the case  .Following[12], we define
.Following[12], we define 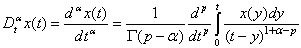
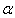 , the order of the operation is a positive real number and
, the order of the operation is a positive real number and 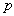 is an integer that satisfies
is an integer that satisfies 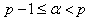 . Setting
. Setting 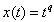 in Eq. (9) and performing the resulting integration as
in Eq. (9) and performing the resulting integration as  , we easily obtain the important formula
, we easily obtain the important formula 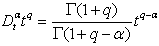
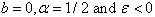 was discussed in[12] using the ADM and series method. Also the comprehensive stability analysis of the special case of Eq. (7) where,
was discussed in[12] using the ADM and series method. Also the comprehensive stability analysis of the special case of Eq. (7) where, 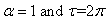 which gives rise to Eq. (3) was discussed in[6].
which gives rise to Eq. (3) was discussed in[6]. 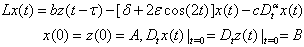
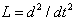 is an easily invertible linear operator. In view of the ADM, we write Eq. (11) as
is an easily invertible linear operator. In view of the ADM, we write Eq. (11) as 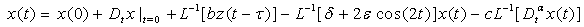
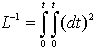 . Employing the initial conditions given in Eq. (8), Eq. (12) becomes
. Employing the initial conditions given in Eq. (8), Eq. (12) becomes 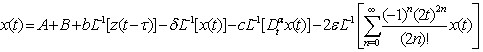
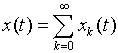
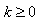 :
: 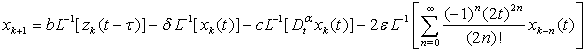
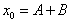 . In the light of Eq. (12) and aided by the following relation
. In the light of Eq. (12) and aided by the following relation 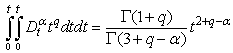
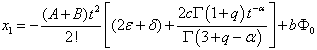
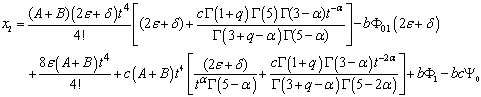
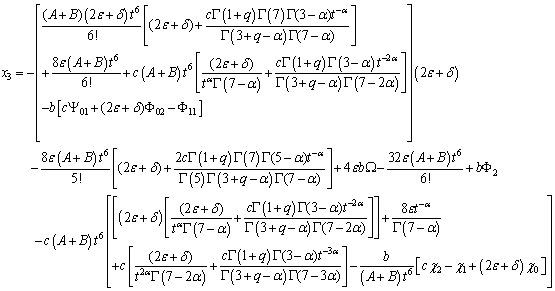
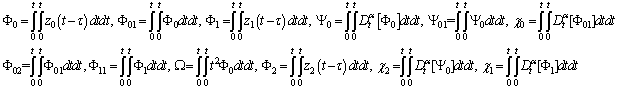 Proceeding in the same manner, one may obtain the other higher components of the solution. We remark here that the convergence of solutions obtained through ADM has been meticulously proved in[31-32].
Proceeding in the same manner, one may obtain the other higher components of the solution. We remark here that the convergence of solutions obtained through ADM has been meticulously proved in[31-32].
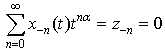
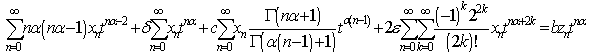
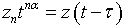 . Note that
. Note that 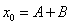 , equating the powers of
, equating the powers of 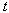 in Eq. (22) we can easily obtain the components of the solution for the given parameters.
in Eq. (22) we can easily obtain the components of the solution for the given parameters. 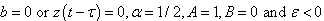 , we obtain from Eq. (8)
, we obtain from Eq. (8) 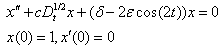
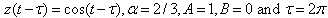 , we obtain from Eq. (8)
, we obtain from Eq. (8)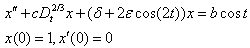
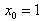 and
and 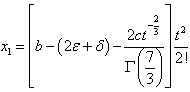
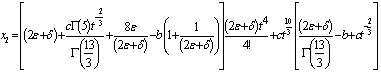
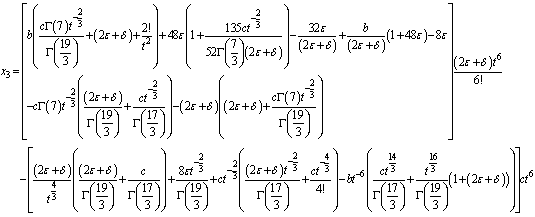
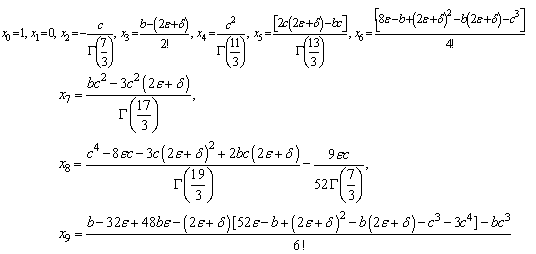
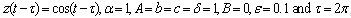 , we obtain from Eq. (8)
, we obtain from Eq. (8)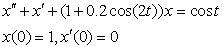
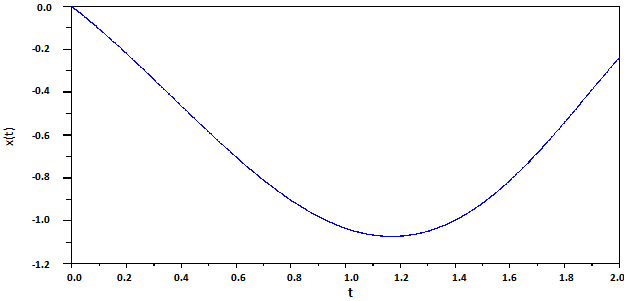
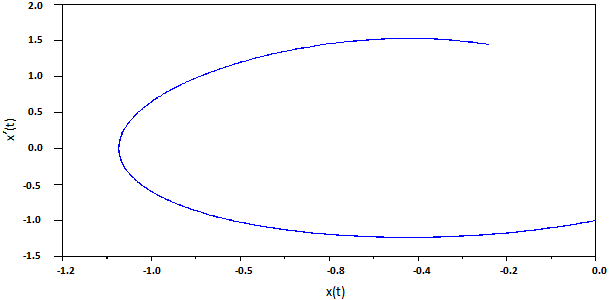
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML