| [1] | E. J. Hinch. Perturbation Methods, Cambridge Texts in Applied Mathematics, Cambridge University Press, Cambridge, 1991. |
| [2] | A. H. Nayfeh. Problems in Perturbation, Wiley, New York, 1985. |
| [3] | A. H. Nayfeh. Perturbation Methods, Wiley, New York, 2000. |
| [4] | W. E Boyce and R. C Diprima. Elementary Differential Equations and Boundary Value Problems, John Wiley & Sons, Inc., 2000. |
| [5] | S.J. Liao. An analytic approximate technique for free oscillations of positively damped systems with algebraically decaying amplitude. Int. J. Nonlinear Mech. 38, 1173-1183, 2003. |
| [6] | S.J. Liao. An analytic approximation of the drag coefficient for viscous flow past a sphere. Int. J. Nonlinear Mechanics, 37, 1-18, 2002. |
| [7] | S.J. Liao. A simple way to enlarge the convergence region of perturbation approximations. Int. J. Nonlinear Dynamics, 19 (2), 91-110, 1999. |
| [8] | S.J. Liao. A uniformly valid analytic solution of 2D viscous flow past a semi-infinite flat plate. J. Fluid Mech. 385, 101-128, 1999. |
| [9] | S.J. Liao. An explicit, totally analytic approximation of Blasius viscous flow problems. Int. J. Nonlinear Mechanics, 34 (4), 759-778, 1999. |
| [10] | S.J. Liao. A kind of approximate solution technique which does not depend on small parameters (ii): an application in fluid mechanics. Int. J. Nonlinear Mechanics, 32, 815-822, 1997. |
| [11] | S.J. Liao. A kind of approximate solution technique which does not depend on small parameters: a special example. Int. J. Nonlinear Mechanics, 30, 371-380, 1995. |
| [12] | S.J. Liao. The proposed homotopy analysis techniques for the solutions of nonlinear problems. Ph.D. Thesis, Shanghai Jiao Tong University, 1992. |
| [13] | S.J. Liao and A. Campo. Analytic solutions of temperature distributions in Blasius viscous flow problems. J. Fluid Mech. 453, 411-425, 2002. |
| [14] | S.J. Liao and A.T. Cheung 1998. Application of homotopy analysis method in nonlinear oscillations. ASME J. Appl. Mech. 65, 914-922. |
| [15] | J. H. He. The homotopy perturbation method for nonlinear oscillators with discontinuities, Appl.Math.Comput.151, 287-292, 2004. |
| [16] | D. D. Ganji. Assessment of homotopy perturbation and perturbation methods in heat radiation equations ,International communications in Heat and mass transfer, 33(3) , 391-400, 2006. |
| [17] | M. Esmaeilpour and D. D. Ganji. A study on generalized coutte flow by He’s methods and comparison with the Numerical solution. World Appl.sci. J. 4(4), 470-478, 2008. |
| [18] | M. J. Hosseni, M. Gorji and M. Ghanbarpour. Solution of temperature Distribution in a Radiating Fin using Homotopy perturbation method. Mathematical problems in Engineering, Article I D: 831362, 8, 2009. |
| [19] | J. H. He. An Elementary introduction to the homotopy perturbation method. Computers and Mathematics with Applications, 57(3), 410-412, 2009. |
| [20] | B. Raftari. Application of He’s homotopy perturbation method and variational iteration method for Nonlinear partial Integro-differential Equations, World Appl.sci. .J. 7(4), 399-404, 2009. |
| [21] | C. Chum and R. Sakthivel. Homotopy perturbation technique for solving two-point boundary value problems-comparison with other methods, Computer Physics Communications 181, 1021-1024, 2010. |
| [22] | A. Fereidoon, D. D. Ganji, H. D. Kaliji and M. Ghadimi. Analytical solution for vibration of buckled beams. Int. J. Res. and Rev. in Appl. Sci. 4(3), 17-21, 2010. |
| [23] | A. Fereidon, Y. Rostamiyan, M. R. avouabadi, S. D. farahni and D. D. Ganji. Analytic Approach to investigation of Distributions of stresses and Radial Displacement at the thick-wall cylinder under the internal and external pressures. Middle-East Journal of scientific Res., 5(5), 321-328, 2010. |
| [24] | F. Farrokhzad, P. Mowlaee, A. Barari, A. J. Choobbasti and H. D. Kaliji. Analytical investigation of beam deformation equation using perturbation, homotopy perturbation, variational iteration and optimal homotopy asymptotic methods. Carpathian Journal of Mathematics, 27(1), 51-63, 2011. |
| [25] | J. H. He. Non-perturbative methods for strongly Nonlinear problems, first Edition, Donghua University Publication, 2006. |
| [26] | J. H. He. Variational approach for nonlinear oscillators. Chaos, Solitons and Fractals 34, 1430-1439, 2007. |
| [27] | J. H. He. Determination of limit cycles for strongly nonlinear oscillators. Phys.Rev.Lett.90, 174-176, 2006. |
| [28] | M. Momeni, N. Jamshidi, A. Barari, D. D. Ganji. Application of He’s energy balance method to Duffing harmonic oscillators. Inter. J. Computer Mathematics DOI:10,1080 / 00207160903337239, 2010. |
| [29] | Mahmoud Bayat, M. Shahidi and Mahdi Bayat. Application of Iteration perturbation method for nonlinear oscillators with discontinuities. International Journal of the Physical Sciences 6(15), 3624-3628, 2011. |
| [30] | S. S. Ganji, A. Barari, S. Karimpour, G. Domairry. Motion of a rigid rod rocking back and forth and cubic-quintic Duffing oscillators. Journal of Theoretical and Applied Mechanics 50(1), 215-229, 2012. |
| [31] | J. H. He. Variational Iteration method-some recent results and new interpretations, Journal of Computational and Applied Mathematics, 207, 3-17, 2007. |
| [32] | A. Barari, M. Omidvar, A. R. Ghotbi and D. D. Ganji. Application of homotopy perturbation method and variational iteration method to nonlinear oscillator differential equations. Acta Applicandae Mathematicae, 104, 161-171, 2008. |
| [33] | M. A. Noor and S. T. Mohyud-Din. Modified variational iteration method for Goursat and Laplace problems, World Applied sciences Journal 4(4), 487-498, 2008. |
| [34] | A. Fereidon, M .Ghadimi, H. D. kaliji, M. Eftari and S. Alinia. Variational Iteration Method for Nonlinear vibration of systems with linear and Nonlinear stiffness, International Journal of Research and Review in Applied Sciences 5(3), 260-263, 2010. |
| [35] | J. H. He, M. G. Wu and F. Austin. The Variation Iteration method which should be followed, Nonlinear Science letters A.,1(1), 1-30, 2010. |
| [36] | N. Herisanu and V. Marinca. A Modified variational Iteration method for strongly Nonlinear problems, Nonlinear science letters A., 1(2), 183-192, 2010. |
| [37] | N. Jamshidi and D. D. Ganji. Application of Energy balance method and variational Iteration method to an oscillation of a mass attached to a stretched elastic wire,Current Applied physics,10, 484-486, 2010. |
| [38] | A. Barari, H. D. kaliji, M. Ghadimi and G. Domairry. Nonlinear vibration of Euler-Bernoulli beams, Latin American Journal of solids and structures, 8(2), 139-148, 2011. |
| [39] | Y. Nawaz. Variational Iteration method and homotopy perturbation method for fourth fractional integro-differential equations , Computers and Mathematics with Applications, 61,2330-2341, 2011. |
| [40] | M. Akbarzade and D. D. Ganji. Coupled method of Homotopy perturbation method and Variational approach for solution to nonlinear cubic-quintic Duffing oscillator, Adv. Theor. Appl. Mech., 3(7), 329-337, 2010. |
| [41] | J. C. Lesage and M. C. Liu. On the investigation of a restrained cargo system modeled as a Duffing oscillator of various orders. Proceedings of ECTC ( Early Career Technical Conference ) ASME, Maimi, Florida, USA, 2008. |

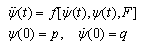
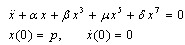
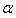 is the resonant frequency,
is the resonant frequency, 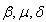 are the nonlinear coefficients.
are the nonlinear coefficients.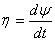 and then (1) can be represented by the system
and then (1) can be represented by the system 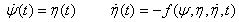
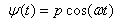
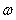 is the angular frequency of oscillation and
is the angular frequency of oscillation and 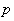 is the initial amplitude of oscillation. Then we obtain using (4) and (3)
is the initial amplitude of oscillation. Then we obtain using (4) and (3) 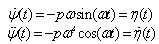
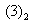 , we obtain
, we obtain 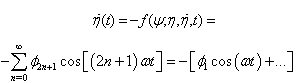
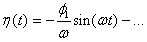
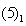 and (7), we obtain
and (7), we obtain 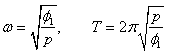
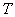 is the period of oscillation. Then we can represent the solution to (1) as
is the period of oscillation. Then we can represent the solution to (1) as 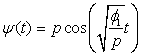
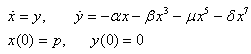
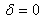 in (2) gives us the popular cubic-quintic Duffing equation while setting
in (2) gives us the popular cubic-quintic Duffing equation while setting 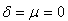 in (2) as well gives the conventional cubic Duffing equation.We assume that the solution to (2) can be expressed in the form of (4). Substituting (4) into (10) yields
in (2) as well gives the conventional cubic Duffing equation.We assume that the solution to (2) can be expressed in the form of (4). Substituting (4) into (10) yields 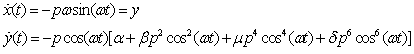
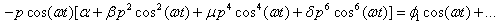
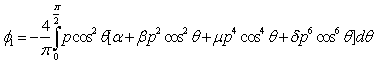
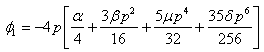
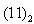 as
as 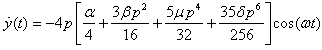
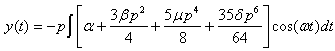
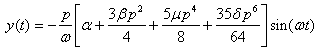
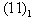 yields
yields 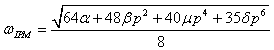
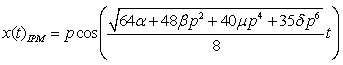
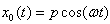 . Following[34], the angular frequency
. Following[34], the angular frequency 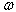 is determined by
is determined by 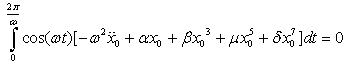
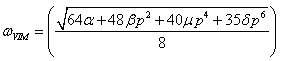
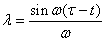
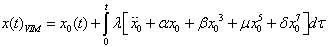
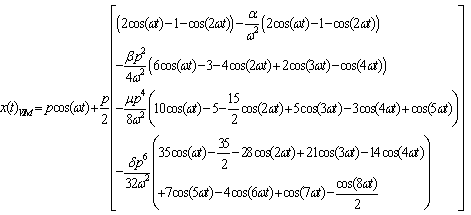
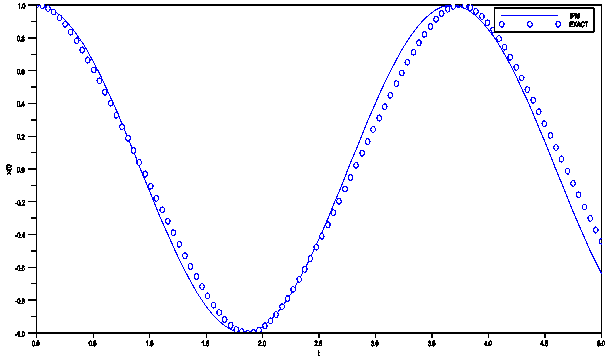
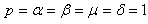

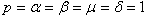
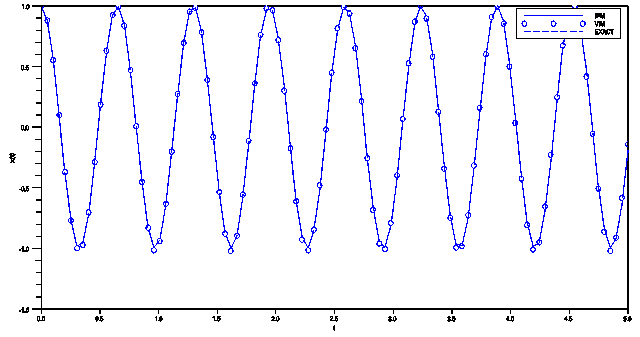
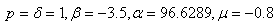
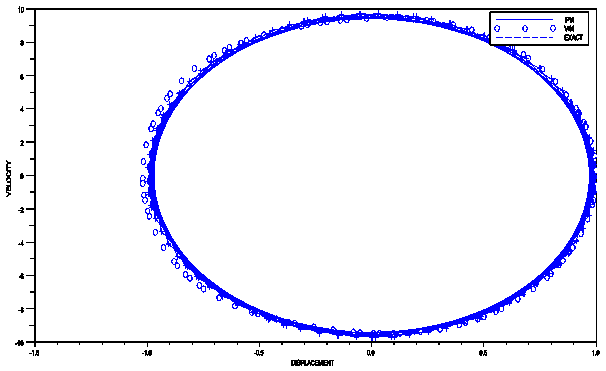
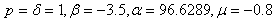
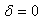 in (19) yields
in (19) yields 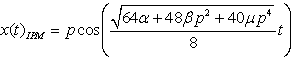
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML