-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Mechanics and Applications
p-ISSN: 2165-9281 e-ISSN: 2165-9303
2013; 3(2): 35-43
doi:10.5923/j.mechanics.20130302.01
Duffing Oscillator with Heptic Nonlinearity under Single Periodic Forcing
M. O. Oyesanya, J. I. Nwamba
Department of Mathematics, University of Nigeria, Nsukka 410001, Nigeria
Correspondence to: M. O. Oyesanya, Department of Mathematics, University of Nigeria, Nsukka 410001, Nigeria.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
In this paper, the Homotopy Analysis Method (HAM) is used to obtain an accurate analytical two-term approximate solution to the positively damped cubic-quintic-heptic Duffing equation with algebraically decaying amplitude as well as a single periodic forcing. This paper also presents the interesting behavior of the non-zero auxiliary parameter which provides a convenient way to adjust and control the convergence of the approximations. Our analysis shows that neither the strength of the damping nor that of the forcing exerts any influence on the auxiliary parameter of the nonlinearity. We observe also that the degree of damping is elicited by the degree of nonlinearity and the initial guesses of the time constants
Keywords: Homotopy Analysis, Duffing Oscillator, Heptic Nonlinearity, Periodic Forcing, Damping
Cite this paper: M. O. Oyesanya, J. I. Nwamba, Duffing Oscillator with Heptic Nonlinearity under Single Periodic Forcing, International Journal of Mechanics and Applications, Vol. 3 No. 2, 2013, pp. 35-43. doi: 10.5923/j.mechanics.20130302.01.
Article Outline
1. Introduction
- The Duffing equations have been presented in the literature considering various types of nonlinearity. Pirbodaghi et al[1] have worked on the Duffing equations with cubic and quintic nonlinearities. Some authors[2], [3],[4],[5][6 ],[7] and[8] have investigated many kinds of nonlinear oscillatory systems in physics, mechanics and engineering. Duffing equations with cubic and quintic nonlinearities have not been extensively studied as the one with cubic nonlinearity because of its complexity[9, 10, 11, 12]. The cubic nonlinear Duffing oscillator had been studied extensively and has been used as model for seismic analysis[13]) and for earthquake prediction[5]. Recently the cubic-quintic nonlinearity in Duffing oscillator has been engaging attention[14, 6, 15] and very interesting features have been detected which were non-existent in the cubic nonlinear model. Interesting results have been obtained from the geometric and analytic studies of the un-damped and unforced cubic-quintic Duffing equation using different methods[1, 16, 17]. It has been observed that the cubic-quintic nonlinearity gives vent to damping in a morepronounced way than the cubic nonlinearity. We therefore in this paper investigate the influence of higher nonlinearity particularly heptic nonlinearity on the damping of Duffing oscillator. The nth-order Duffing equation with viscous damping and periodic forcing can be generally expressed as
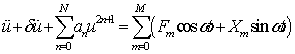 | (1.0) |
 are arbitrary constants,
are arbitrary constants,  In this paper the homotopy analysis method[18, 19,20]which has been effectively applied to a wide variety of problems in applied mathematics, physics and engineering is applied to the positively damped cubic-quintic-heptic Duffing equation with a single sinusoidal forcing governed by
In this paper the homotopy analysis method[18, 19,20]which has been effectively applied to a wide variety of problems in applied mathematics, physics and engineering is applied to the positively damped cubic-quintic-heptic Duffing equation with a single sinusoidal forcing governed by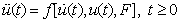 | (1.1) |
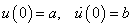 | (1.2) |
 to construct a new kind of homotopy in a more general form has the following advantages:1). It is valid even if a given nonlinear problem does not contain any small/large parameters at all.2). It equips us with a convenient way to adjust and control convergence regions of series of analytic approximations.3). It can be efficiently employed in approximating a nonlinear problem by choosing different sets of base functions.We investigate here factors that influence the non-zero auxiliary parameter g.Free oscillations of a positively damped system have two different time scales. One is related to the frequency of oscillationandthe other to the decaying amplitude of oscillation. It is clear that the free oscillation of positively damped systems can be expressed by the set of base functions
to construct a new kind of homotopy in a more general form has the following advantages:1). It is valid even if a given nonlinear problem does not contain any small/large parameters at all.2). It equips us with a convenient way to adjust and control convergence regions of series of analytic approximations.3). It can be efficiently employed in approximating a nonlinear problem by choosing different sets of base functions.We investigate here factors that influence the non-zero auxiliary parameter g.Free oscillations of a positively damped system have two different time scales. One is related to the frequency of oscillationandthe other to the decaying amplitude of oscillation. It is clear that the free oscillation of positively damped systems can be expressed by the set of base functions 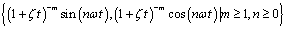 | (1.3) |
 relate to the two time scales
relate to the two time scales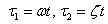 | (1.4) |
 and given by
and given by 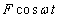 | (1.5) |
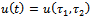 , and the original governing equation (1.1) becomes
, and the original governing equation (1.1) becomes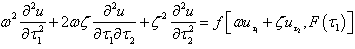 | (1.6) |
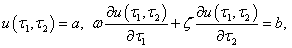 when
when 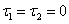 | (1.7) |
2. Basic Ideas
- A real function can be efficiently represented by a better set of base functions. Hence, the need to approximate a given nonlinear problem by a proper set of base functions equips us with the initiative to apply the homotopy analysis method. Clearly, according to (1.3) and the definition (1.4), the considered problem can be represented by (1.3) such that
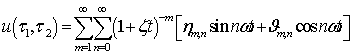 | (2.0) |
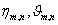 arecoefficients. This provides us with a rule, called the Rule of Solution Expression[15].As was noted in[20], HAM is based on continuous variations from the initial guesses to the exact solution of a considered problem. For the problem under consideration, one constructs the continuous mapping
arecoefficients. This provides us with a rule, called the Rule of Solution Expression[15].As was noted in[20], HAM is based on continuous variations from the initial guesses to the exact solution of a considered problem. For the problem under consideration, one constructs the continuous mapping 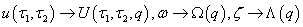 in such a way that
in such a way that 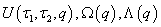 vary from their initial guesses
vary from their initial guesses 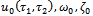 to their exact solutions
to their exact solutions 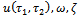 respectively as
respectively as 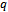 ( the embedding parameter ) increases from 0 to 1. In line with the above reasons one constructs a family in q of nonlinear differential equations
( the embedding parameter ) increases from 0 to 1. In line with the above reasons one constructs a family in q of nonlinear differential equations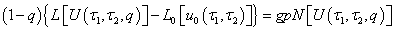 | (2.1) |
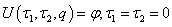 | (2.2) |
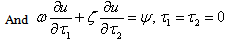 | (2.3) |
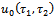 is an initial guess of
is an initial guess of 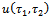 ,
,  is a nonlinear operator defined by
is a nonlinear operator defined by 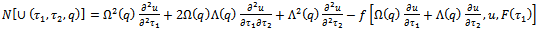 | (2.4) |
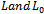 are two auxiliary linear operators defined by
are two auxiliary linear operators defined by 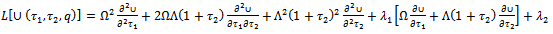 | (2.5) |
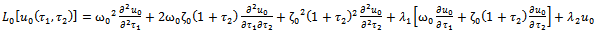 | (2.6) |
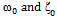 are initial guesses of the time-constants
are initial guesses of the time-constants 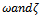 respectively, and
respectively, and 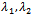 are two constants to be determined later in terms of
are two constants to be determined later in terms of 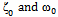 respectively. The auxiliary non-zero parameter
respectively. The auxiliary non-zero parameter 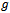 equips us with a convenient way to adjust and control the convergence of approximations such that a properly chosen
equips us with a convenient way to adjust and control the convergence of approximations such that a properly chosen 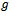 guarantees the convergence of the resulting series to be given later at
guarantees the convergence of the resulting series to be given later at 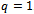 .Under the Rule of Solution Expression[20], one chooses
.Under the Rule of Solution Expression[20], one chooses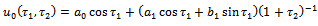 | (2.7) |
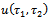 , where
, where 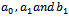 are unknown constants to be determined later.When
are unknown constants to be determined later.When 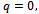 Eq. (2.1) has the solution (2.7) with
Eq. (2.1) has the solution (2.7) with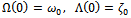 | (2.8) |
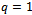 , Eqs. (2.1)-(2.3) becomes exactly (1.6) and (1.7) as long as
, Eqs. (2.1)-(2.3) becomes exactly (1.6) and (1.7) as long as 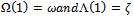 .Thus,
.Thus, 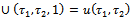 | (2.9) |
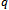 increases from 0 to 1,
increases from 0 to 1, 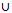 truly varies from the initial trial
truly varies from the initial trial 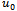 to the exact solution
to the exact solution 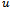 of the original equations (1.6) and (1.7); so do
of the original equations (1.6) and (1.7); so do 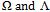 vary from the initial guesses to the time-constants
vary from the initial guesses to the time-constants 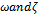 respectively. Equations (2.1)-(2.3) are the zeroth-order deformation equations.With the nature of (2.8),
respectively. Equations (2.1)-(2.3) are the zeroth-order deformation equations.With the nature of (2.8), 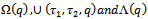 can be expanded in power series of
can be expanded in power series of 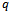 by Taylor’s theorem as:
by Taylor’s theorem as: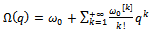 | (2.10) |
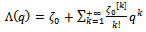 | (2.11) |
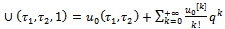 | (2.12) |
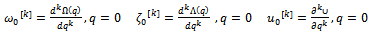 | (2.13) |
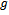 influences the convergence of the series (2.10) – (2.12).A convergent series given by the HAM
influences the convergence of the series (2.10) – (2.12).A convergent series given by the HAM 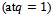 must be an exact solution of the considered problem as was proved in[8]. Hence, one obtains
must be an exact solution of the considered problem as was proved in[8]. Hence, one obtains 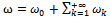 | (2.14) |
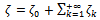 | (2.15) |
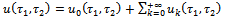 | (2.16) |
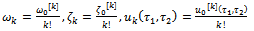 | (2.17) |
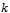 times with respect to
times with respect to 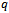 and then set
and then set 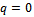 and finally divide them by
and finally divide them by 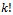 . We obtain the so-called
. We obtain the so-called 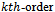 deformation equation[2]
deformation equation[2]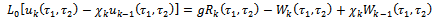 | (2.18) |
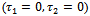
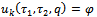 | (2.19) |
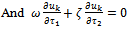 | (2.20) |
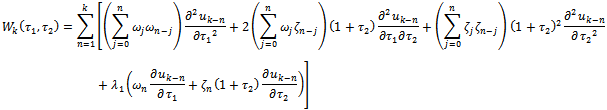 | (2.21) |
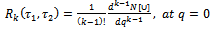 | (2.22) |
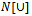 is given by (2.4) and
is given by (2.4) and 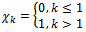 | (2.23) |
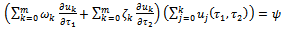 | (2.24) |
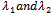 , we demand that for any constants
, we demand that for any constants 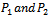 the equation
the equation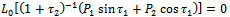 | (2.25) |
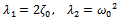 | (2.26) |
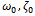 play a crucial role in determining the initial guess
play a crucial role in determining the initial guess 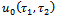 and the auxiliary linear operators
and the auxiliary linear operators 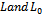 .However we must take note of the existence of the terms
.However we must take note of the existence of the terms 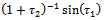 and
and 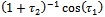 on the right hand side of (2.18). Their existence goes contrary to the Rule of Solution Expression, which is clearly described by (2.0). Therefore, for a uniformly valid solution, one has to set the coefficients of these two terms to zero.We must as well note that for un-damped systems,
on the right hand side of (2.18). Their existence goes contrary to the Rule of Solution Expression, which is clearly described by (2.0). Therefore, for a uniformly valid solution, one has to set the coefficients of these two terms to zero.We must as well note that for un-damped systems,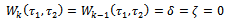 | (2.27) |
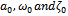 initially.
initially.3. Application of HAM
- Writing (1.1) explicitly under the transformations given in (1.4), we obtain
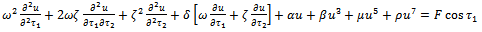 | (3.0) |
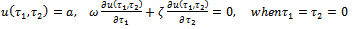 | (3.1) |
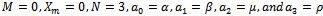 , after which the transformation depicted by (1.4) is used.We construct such a family of equations as described by (2.1) where the auxiliary linear operator is given by
, after which the transformation depicted by (1.4) is used.We construct such a family of equations as described by (2.1) where the auxiliary linear operator is given by 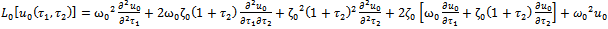 | (3.2) |
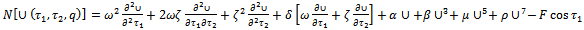 | (3.3) |
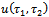 as
as 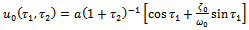 | (3.4) |
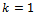 in (2.18) to obtain
in (2.18) to obtain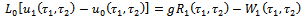 | (3.5) |
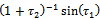 and
and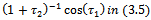 . The results obtained respectively are as follows:
. The results obtained respectively are as follows: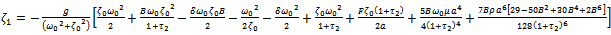 | (3.6) |
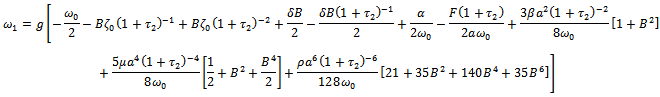 | (3.7) |
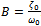 .After eliminating terms that brings non-uniformity equation (3.5) becomes
.After eliminating terms that brings non-uniformity equation (3.5) becomes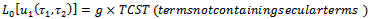 | (3.8) |
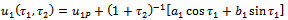 | (3.9) |
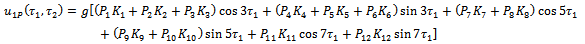 | (3.10) |
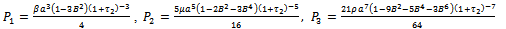 | (3.11) |
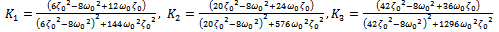 | (3.12) |
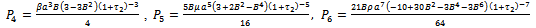 | (3.13) |
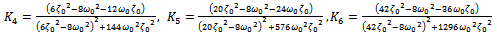 | (3.14) |
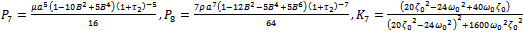 | (3.15) |
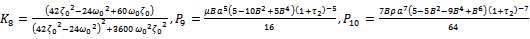 | (3.16) |
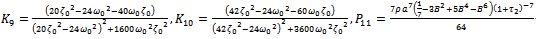 | (3.17) |
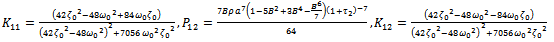 | (3.18) |
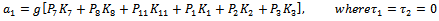 | (3.19) |
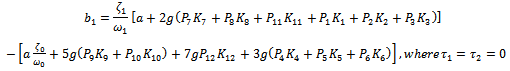 | (3.20) |
- Following the same procedure, one can obtain
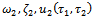 and so on.We must note that for the application done above, we have chosen
and so on.We must note that for the application done above, we have chosen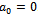 . This choice is not mandatory, but
. This choice is not mandatory, but 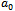 must be chosen to be so close to zero or zero. The general rule for choosing
must be chosen to be so close to zero or zero. The general rule for choosing 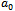 was also given in[20].
was also given in[20].4. Results
- In this section we use the results given above to obtain the solutions to 1). Positively damped cubic-quintic Duffing equation with a single periodic forcing.2). Positively damped and unforced cubic-quintic-heptic Duffing equation.3). Un-damped cubic-quintic-heptic Duffing equation with a single periodic forcing.4). Un-damped and unforced cubic-quintic-heptic Duffing equation.5). Un-damped cubic-quintic Duffing equation with a single periodic forcing.6). Un-damped and unforced cubic-quintic Duffing equation.After applying the transformation in (1.4) and subject to the initial conditions prescribed in (3.1), the positively damped cubic-quintic Duffing equation with a single periodic forcing is obtained from (1.0) by setting
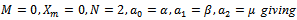
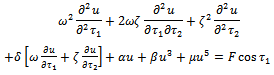 | (4.0) |
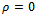 in (3.9), (3.7) and (3.6) one obtains the first-order approximate solution to (4.0) with the same initial guess given in (3.4). Consequently, other higher-order approximate solutions to (4.0) can as well be obtained provided
in (3.9), (3.7) and (3.6) one obtains the first-order approximate solution to (4.0) with the same initial guess given in (3.4). Consequently, other higher-order approximate solutions to (4.0) can as well be obtained provided  . After applying the transformation in (1.4) and subject to the initial conditions prescribed in (3.1) the positively damped and unforced cubic-quintic-heptic Duffing equation is obtained by setting
. After applying the transformation in (1.4) and subject to the initial conditions prescribed in (3.1) the positively damped and unforced cubic-quintic-heptic Duffing equation is obtained by setting 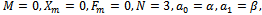
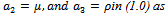
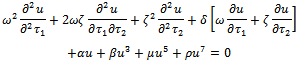 | (4.1) |
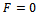 in (3.7) and (3.6), we obtain the first-order approximate solution to (4.1) as given in (3.9) with the same initial guess function given in (3.4). The other higher-order approximate solutions to (4.1) can also be obtained as long as
in (3.7) and (3.6), we obtain the first-order approximate solution to (4.1) as given in (3.9) with the same initial guess function given in (3.4). The other higher-order approximate solutions to (4.1) can also be obtained as long as 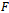 remains zero.Setting
remains zero.Setting 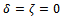 in (3.9), (3.7), (3.6) and (3.4) one obviously obtains the initial guess function ,the first approximation to its frequency and the first-order approximate solution to the un-damped cubic-quintic-heptic Duffing equation with a single periodic forcing which can be obtained from (1.0) by taking
in (3.9), (3.7), (3.6) and (3.4) one obviously obtains the initial guess function ,the first approximation to its frequency and the first-order approximate solution to the un-damped cubic-quintic-heptic Duffing equation with a single periodic forcing which can be obtained from (1.0) by taking 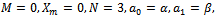
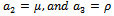 and given by
and given by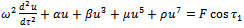 | (4.2) |
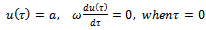 | (4.3) |
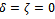 by taking
by taking 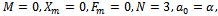
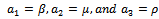 . Higher-order approximate solutions can as well be obtained.Setting
. Higher-order approximate solutions can as well be obtained.Setting 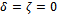 in (3.9), (3.7), (3.6) and (3.4) one also obtains the initial guess function,the first frequency approximation and the first-order approximate solution to the un-damped cubic-quintic Duffing equation with a single periodic forcing which can be obtained from (1.0) by taking
in (3.9), (3.7), (3.6) and (3.4) one also obtains the initial guess function,the first frequency approximation and the first-order approximate solution to the un-damped cubic-quintic Duffing equation with a single periodic forcing which can be obtained from (1.0) by taking 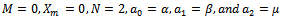 and given by
and given by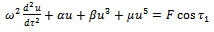 | (4.4) |
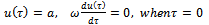 | (4.5) |
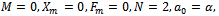
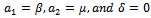 and is given by
and is given by 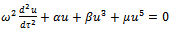 | (4.6) |
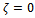 , after applying the transformation in (1.4) and subject to the initial conditions prescribed in (4.3).By enforcing
, after applying the transformation in (1.4) and subject to the initial conditions prescribed in (4.3).By enforcing 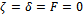 in (3.9),(3.7),(3.6) and (3.4), one as well obtains the first-order approximate solution and the first frequency approximation to (4.6) as given in (3.9). The other higher-order approximate solutions to (4.1) can also be obtained as long as
in (3.9),(3.7),(3.6) and (3.4), one as well obtains the first-order approximate solution and the first frequency approximation to (4.6) as given in (3.9). The other higher-order approximate solutions to (4.1) can also be obtained as long as  remains zero. We note that the first frequency approximation and the first-order approximate solution to (4.6) obtained by setting some parameters above equal to zero is exactly the same results obtained in[22].Below are presented some of the simulations we did, in Figure One and Figure Two, we observe the behavior of the damped and forced cubic-quintic-heptic Duffing oscillator.FigureThree and Figure Four depict the behavior of the damped and forced cubic-quintic Duffing oscillator. We also did a lot of simulations using different values for our parameters to observe the behavior of the auxiliary non-zero parameter which controls the convergence of our approximations.Interestingly neitherthe strength of the dampingnor that of the forcing exert any influenceon
remains zero. We note that the first frequency approximation and the first-order approximate solution to (4.6) obtained by setting some parameters above equal to zero is exactly the same results obtained in[22].Below are presented some of the simulations we did, in Figure One and Figure Two, we observe the behavior of the damped and forced cubic-quintic-heptic Duffing oscillator.FigureThree and Figure Four depict the behavior of the damped and forced cubic-quintic Duffing oscillator. We also did a lot of simulations using different values for our parameters to observe the behavior of the auxiliary non-zero parameter which controls the convergence of our approximations.Interestingly neitherthe strength of the dampingnor that of the forcing exert any influenceon 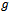 for all the different cases we treated. It was rather the initial guesses of the time constants
for all the different cases we treated. It was rather the initial guesses of the time constants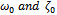 , and of course as was noted in[20] the strength of the nonlinearity that determines and influences
, and of course as was noted in[20] the strength of the nonlinearity that determines and influences 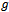 . Furthermore, just as was noted in[20], problems with stronger nonlinearity demands that we choose
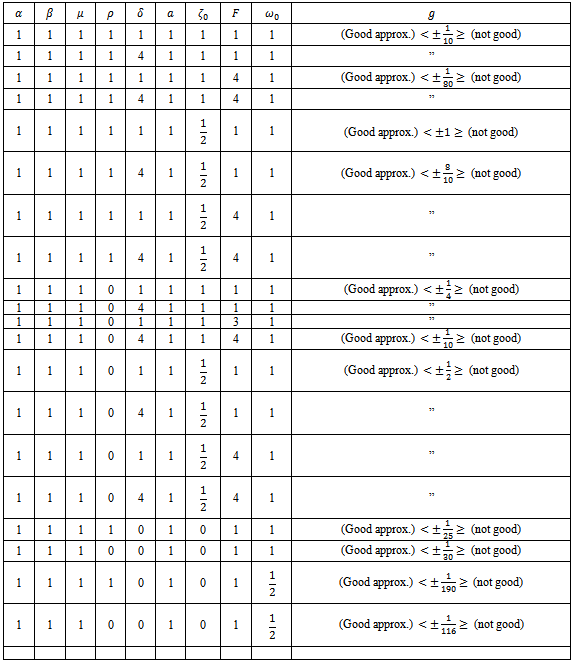
. Furthermore, just as was noted in[20], problems with stronger nonlinearity demands that we choose 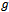 such that its absolute value lies very close to zero but must not be zero.The table below depictssome of these interesting behaviorsof
such that its absolute value lies very close to zero but must not be zero.The table below depictssome of these interesting behaviorsof 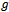 .
.
|
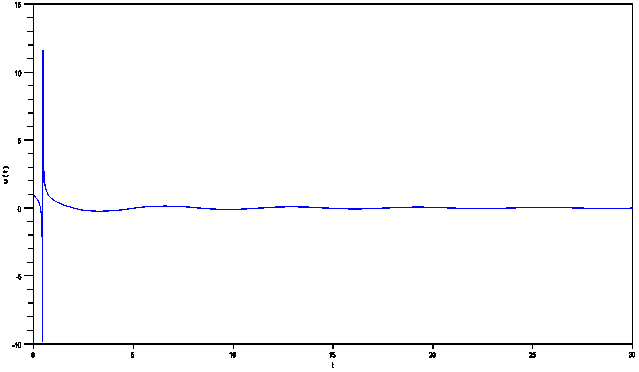 | Figure 1. 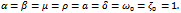 Behavior of the displacement of the damped and forced cubic-quintic-heptic Duffing oscillator as time increases for Behavior of the displacement of the damped and forced cubic-quintic-heptic Duffing oscillator as time increases for 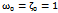 |
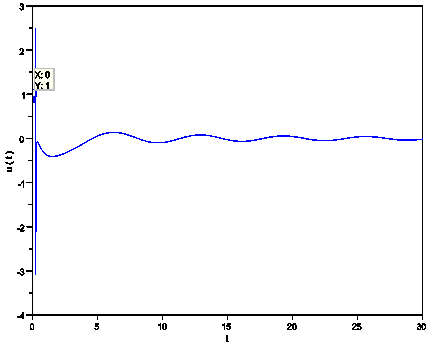 | Figure 2. 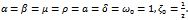 Behavior of the displacement of the damped and forced cubic-quintic-heptic Duffing oscillator as time increases for Behavior of the displacement of the damped and forced cubic-quintic-heptic Duffing oscillator as time increases for 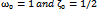 |
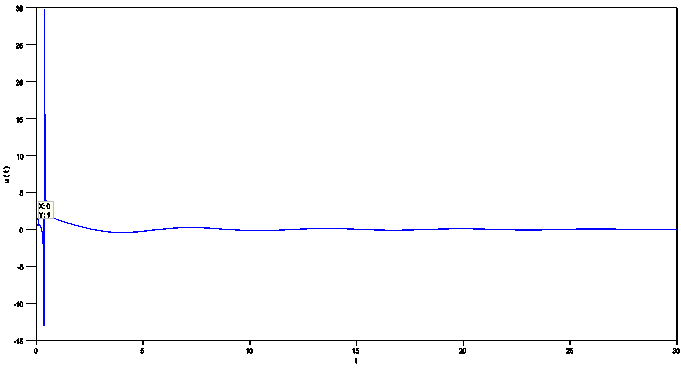 | Figure 3. 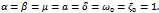 Behavior of the displacement of the damped and forced cubic-quintic Duffing oscillator as time increases for Behavior of the displacement of the damped and forced cubic-quintic Duffing oscillator as time increases for 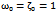 |
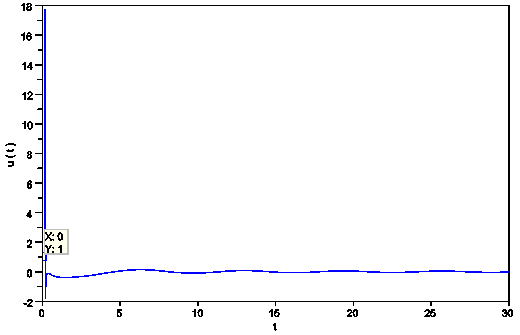 | Figure 4.  .Behavior of the displacement of the damped and forced cubic-quintic Duffing oscillator as time increases for .Behavior of the displacement of the damped and forced cubic-quintic Duffing oscillator as time increases for  |
5. Conclusions
- In this paper, the homotopy analysis method (HAM) was used to obtain analytic and uniformly-valid approximate solutions to the damped and driven, free oscillating, as well as the un-damped and un-driven Duffing oscillator equations with different nonlinearities.It was observed as noted in[6] that the degree of damping is elicited by the degree of nonlinearity as can be seen in Figures 1-4. Hence one can use increased nonlinearity to reduce the effect of external forcing as well as negative damping. We also observed that apart from the strength of the nonlinearity of a given problem, the initial guesses
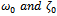 , chosen for any given problem aids in determining a suitable auxiliary non-zero parameter such that, given
, chosen for any given problem aids in determining a suitable auxiliary non-zero parameter such that, given 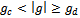 , where
, where 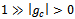 and
and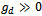 . It is also observed that every chosen g satisfying
. It is also observed that every chosen g satisfying 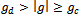 gives a good approximation while every chosen g satisfying
gives a good approximation while every chosen g satisfying 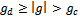 does not give a good approximation. There is need to consider and investigate the degree of nonlinearity that can reduce the effect of external forcing for Duffing oscillator with multiple forcing functions and investigate the influence and the range of validity of the auxiliary parameter. Stability analysis also should engage attention in subsequent work.
does not give a good approximation. There is need to consider and investigate the degree of nonlinearity that can reduce the effect of external forcing for Duffing oscillator with multiple forcing functions and investigate the influence and the range of validity of the auxiliary parameter. Stability analysis also should engage attention in subsequent work.Highlights
- 1. Neither the strength of the damping nor that of the forcing exerts any influence on the auxiliary parameter of the nonlinearity.2. Factors that affect the nonzero auxiliary parameter (which controls the convergence of the approximate solutions obtained) in HAM are shown and discussed. 3. The degree of damping is elicited by the degree of nonlinearity and the initial guesses of the time constants
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML