P. Ponnusamy
Department of Mathematics, Government Arts College, Coimbatore, 641 018, Tamil Nadu, India
Correspondence to: P. Ponnusamy , Department of Mathematics, Government Arts College, Coimbatore, 641 018, Tamil Nadu, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The free vibration analysis of ring shaped plate of polygonal cross-sections immersed in fluid is studied using the Fourier expansion collocation method. The equations of motion based on two-dimensional theory of elasticity is applied under the plane stress-strain assumptions of elastic plate of polygonal cross-sections namely, triangle, square, pentagon and hexagon is made of isotropic material. The frequency equations are obtained for longitudinal and flexural anti symmetric modes of vibrations. The computed non-dimensional frequencies are plotted in the form of dispersion curves for the material copper. Comparison is made between the frequency responses of plate in space and plate immersed in fluid. The general theory can be used to study any kinds of ring shaped plate using the proper geometrical relations.
Keywords:
Solid-Fluid Interface, Wave Propagation in Plate, Vibration of Thermal Plate, Piezoelectric Plate, Plate Immersed in Fluid, Generalized Thermo Elastic Plate, Cylinder Immersed in Fluid
Cite this paper: P. Ponnusamy , Free Vibration Analysis of Ring Shaped Plate of Polygonal Cross-Sections Immersed in Fluid, International Journal of Mechanics and Applications, Vol. 3 No. 1, 2013, pp. 13-25. doi: 10.5923/j.mechanics.20130301.03.
1. Introduction
The plates of circular and plates of polygonalcross-sections are often used as structural components and their vibration characteristics are important for practical design. The frequency responses of rotating arbitrary / polygonal cross-sectional plates has many applications in various fields of science and technology, namely, submarine structures, pressure vessel, bore wells, ship building industries and have many other engineering applications. Nagaya[1-3] studied the simplified method for solving problems of vibrating plates of doubly connected arbitrary shape using the Fourier expansion collocation method, he has detained the frequency equations for a doubly connected polygonal cross-sectional plate and numerical calculation were carried for the above said cross-sections. Following Nagaya, Ponnusamy[4,5] discussed the frequency responses of thermo-elastic plate of arbitrary cross-sections and generalized thermo-elastic plate of polygonal cross-sections by using the Fourier expansion collocation method developed by Nagaya[1,-3]. Venkatesan and Ponnusamy[6,7] studied the wave propagation in solid and generalized solid cylinder of arbitrary cross-sections immersed in fluid using the Fourier expansion collocation method. Sinha et al[8] have studied the axisymmetric wave propagation in circular cylindrical shell immersed in a fluid, in two parts. In Part I, the theoretical analysis of the propagation modes is discussed and in Part II, the axisymmetric modes excluding tensional modes are obtained theoretically and experimentally and are compared. Berliner and Solecki[9] have studied the wave propagation in a fluid loaded transversely isotropic cylinder. In that paper, Part I consists of the analytical formulation of the frequency equation of the coupled system consisting of the cylinder with inner and outer fluid and Part II gives the numerical results. Easwaran and Munjal[10] investigated the effect of wall compliance on lowest order mode propagation in a fluid filled or submerged impedance tubes. Based on the closed form analytical solution of the coupled wave equations and applying the boundary conditions at the fluid-solid interface, an eigen equation was obtained and then the dispersion behavior of wave motion was analyzed. Also, they investigated axial attenuation characteristics of plane waves along water filled tubes submerged in water or air. This paper demonstrates the in-plane vibration of rings of polygonal cross section composed of homogeneous isotropic material immersed in a fluid. In the first part, solutions to the equations of motion for an isotropic medium using the two dimensional theory of elasticity and for the fluid in and around the solid medium are described. It is assumed that, there is no vibration and displacement along the z-axis, that is the displacement along the z-axis, 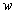 is zero. To satisfy the boundary conditions, the Fourier expansion collocation method is performed to the equations of the boundary conditions along the boundary of the inner and outer surface of the ring. Also, the frequency equations are obtained for the symmetric and antisymmetric cases. To illustrate the validity of the model, some numerical examples are provided for the frequency equation. The equation is solved by omitting the fluid medium and the results are compared with the frequency responses of plate in space and plate immersed in fluid. Also, the results are obtained for polygonal ( triangle, square, pentagon and hexagon) rings for the longitudinal and flexural antisymmetric modes of vibrations.
is zero. To satisfy the boundary conditions, the Fourier expansion collocation method is performed to the equations of the boundary conditions along the boundary of the inner and outer surface of the ring. Also, the frequency equations are obtained for the symmetric and antisymmetric cases. To illustrate the validity of the model, some numerical examples are provided for the frequency equation. The equation is solved by omitting the fluid medium and the results are compared with the frequency responses of plate in space and plate immersed in fluid. Also, the results are obtained for polygonal ( triangle, square, pentagon and hexagon) rings for the longitudinal and flexural antisymmetric modes of vibrations.
2. Formulation of the Problem
We consider a homogeneous, isotropic, elastic ring shaped plate of polygonal cross-sections immersed in fluid. The system displacements and stresses are defined by the polar coordinates r and 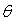 in an arbitrary point inside the plate and denote the displacements
in an arbitrary point inside the plate and denote the displacements 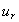 in the direction of r and
in the direction of r and 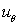 in the tangential direction
in the tangential direction 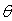 . The in-plane vibration and displacements of ring shaped plate of polygonal cross-sections immersed in fluid is obtained by assuming that there is no vibration and displacement along the z-directions in the cylindrical coordinate system
. The in-plane vibration and displacements of ring shaped plate of polygonal cross-sections immersed in fluid is obtained by assuming that there is no vibration and displacement along the z-directions in the cylindrical coordinate system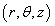 . The two dimensional stress equations of motion, strain displacement relations in the absence of body forces for a linearly elastic medium are considered from Ponnusamy[4] as
. The two dimensional stress equations of motion, strain displacement relations in the absence of body forces for a linearly elastic medium are considered from Ponnusamy[4] as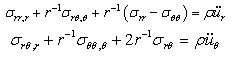 | (1) |
and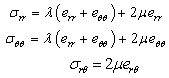 | (2) |
Where 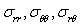 are the stress components,
are the stress components, 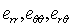 are the strain components,
are the strain components, 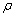 is the mass density,
is the mass density, 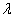 and
and 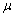 are Lame’s constants. The strain
are Lame’s constants. The strain 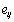 related to the displacements are given by
related to the displacements are given by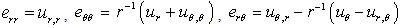 | (3) |
in which 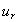 and
and 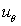 are the displacements components along radial and circumferential directions respectively. The comma in the subscripts denotes the partial differentiation or derivative with respect to the variables.Substituting the Eqs.(2) and (3) in Eqs.(1), the displacement equations of motions are obtained as
are the displacements components along radial and circumferential directions respectively. The comma in the subscripts denotes the partial differentiation or derivative with respect to the variables.Substituting the Eqs.(2) and (3) in Eqs.(1), the displacement equations of motions are obtained as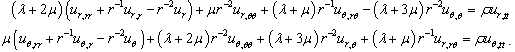 | (4) |
3. Solutions of Ring Shaped Plate
To obtain the free vibration of ring shaped plate of polygonal cross-sections, we seek the solution of Eq.(4) in the form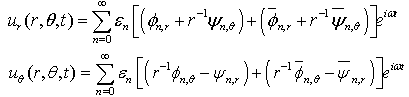 | (5) |
where 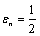 for
for 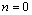 ,
, 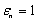 for
for 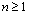 ,
, 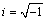 ,
, 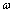 is the frequency,
is the frequency, 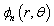 ,
, 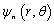 ,
, 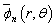 and
and 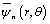 are the displacement potentials. By introducing the dimensionless quantities
are the displacement potentials. By introducing the dimensionless quantities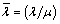 ,
, 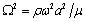 ,
, 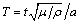 ,
, 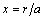 and substituting Eq.(5) in Eq.(4), we obtain
and substituting Eq.(5) in Eq.(4), we obtain 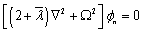 | (6) |
and 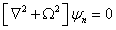 | (7) |
where 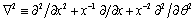 The solution of Eq. (6) for symmetric mode is
The solution of Eq. (6) for symmetric mode is 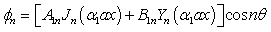 | (8) |
and the solution for the anti symmetric mode 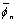 is obtained by replacing
is obtained by replacing 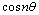 by
by 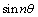 in Eq. (8), we get
in Eq. (8), we get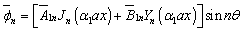 | (9) |
where 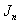 is the Bessel function of first kind of order n and
is the Bessel function of first kind of order n and 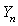 is the Bessel function of second kind of order n and
is the Bessel function of second kind of order n and 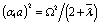 . Solving Eq. (7), we obtain
. Solving Eq. (7), we obtain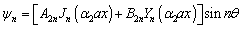 | (10) |
for symmetric mode. For the antisymmetric mode 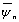 is obtained from Eq. (10) by replacing
is obtained from Eq. (10) by replacing 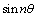 by
by 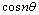 in Eq. (10), we obtain
in Eq. (10), we obtain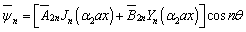 | (11) |
where 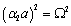 . If
. If 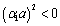 and
and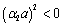 , then the Bessel functions
, then the Bessel functions 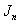 and
and 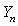 are replaced by the modified Bessel functions
are replaced by the modified Bessel functions 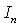 and
and 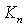 respectively.
respectively.
4. Solutions of Fluid Medium
In cylindrical polar coordinates 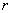 and
and 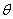 the acoustic pressure and radial displacement equation of motion for an inviscid fluid are of the form Achenbach[11] ,
the acoustic pressure and radial displacement equation of motion for an inviscid fluid are of the form Achenbach[11] ,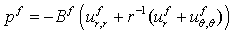 | (12) |
and 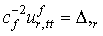 | (13) |
respectively, where 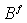 is the adiabatic bulk modulus,
is the adiabatic bulk modulus, 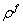 is the density,
is the density, 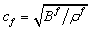 is the acoustic phase velocity in the fluid,
is the acoustic phase velocity in the fluid, 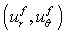 is the displacement vector and
is the displacement vector and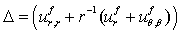 | (14) |
Substitutingand seeking the solution of Eq. (13) in the form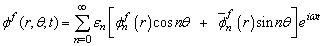 | (16) |
the oscillating waves propagating in the inner fluid located in the annulus is given by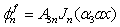 | (17) |
where 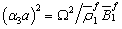 , in which
, in which 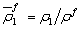 ,
, 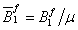 . If
. If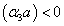 , the Bessel function
, the Bessel function 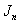 in the Eq. (17) is to be replaced by modified Bessel function
in the Eq. (17) is to be replaced by modified Bessel function 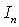 . Similarly, for the outer fluid that represents the oscillatory waves propagating away is given as
. Similarly, for the outer fluid that represents the oscillatory waves propagating away is given as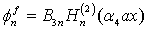 | (18) |
where 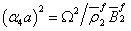 , in which
, in which 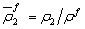 ,
,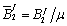 ,
, 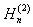 is the Hankel function of the second kind of order n. If
is the Hankel function of the second kind of order n. If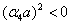 , then the Hankel function of second kind is to be replaced by
, then the Hankel function of second kind is to be replaced by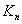 , where
, where 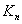 is the modified Bessel function of the second kind. By substituting Eq. (16) in Eq. (12) along with the Eqs. (17) and (18), the acoustic pressure for the inner fluid can be expressed as
is the modified Bessel function of the second kind. By substituting Eq. (16) in Eq. (12) along with the Eqs. (17) and (18), the acoustic pressure for the inner fluid can be expressed as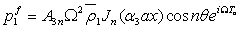 | (19) |
while for the outer fluid, it is given by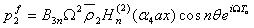 | (20) |
In the antisymmetric case, the solutions for the inner and outer fluid are obtained as 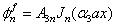 | (21) |
and 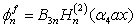 | (22) |
Similarly, the acoustic pressure for the antisymmetric mode are obtained as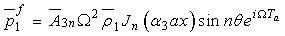 | (23) |
for the inner fluid and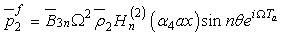 | (24) |
for the outer fluid.
5. Boundary Conditions and Frequency Equations
The boundary conditions along the curved surfaces of the ring are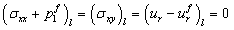 | (25) |
for the inner boundary and 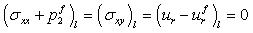 | (26) |
for the outer boundary, where 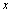 is the coordinate normal to the boundary and
is the coordinate normal to the boundary and 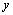 is the coordinate in the tangential direction,
is the coordinate in the tangential direction, 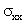 is the normal stress,
is the normal stress, 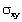 are the shearing stresses and
are the shearing stresses and 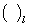 is the value at the
is the value at the 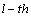 segment of the boundary. The first and last conditions in Eqs. (25) and (26) are due to the continuity of the stresses and displacements of the ring shaped plate and fluid on the curved surfaces. Since the boundary of the cross section is irregular in shape, it is difficult to satisfy the boundary conditions along both inner and outer surfaces of the ring shaped polygonal cross sectional plate immersed in fluid directly. If
segment of the boundary. The first and last conditions in Eqs. (25) and (26) are due to the continuity of the stresses and displacements of the ring shaped plate and fluid on the curved surfaces. Since the boundary of the cross section is irregular in shape, it is difficult to satisfy the boundary conditions along both inner and outer surfaces of the ring shaped polygonal cross sectional plate immersed in fluid directly. If 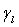 is the angle between normal to the segment and the reference axis and if it is assumed to be constant, then the transformed expressions for the stresses are Nagaya[3] as
is the angle between normal to the segment and the reference axis and if it is assumed to be constant, then the transformed expressions for the stresses are Nagaya[3] as 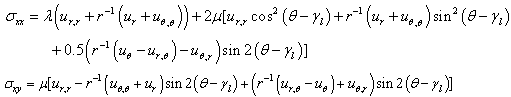 | (27) |
Substituting Eqs. (8)-(11), (19), (20), (23), (24) in the Eqs. (25) and (26), the boundary conditions are transformed as follows: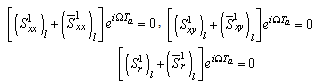 | (28) |
for the inner surface and 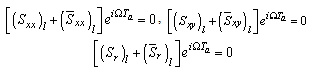 | (29) |
for the outer surface, where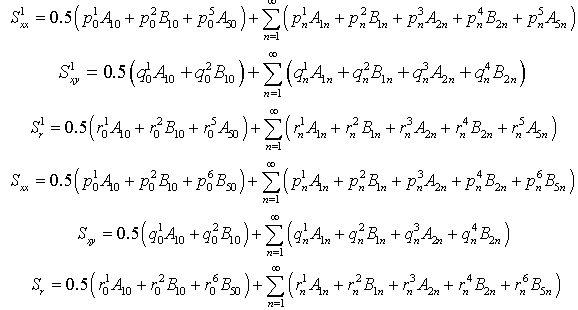 | (30) |
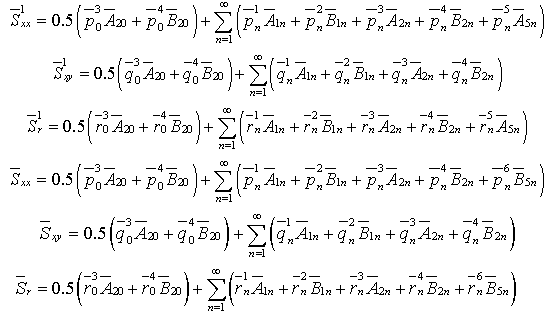 | (31) |
The terms 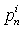 to
to 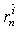 are given in the Appendix A.Performing the Fourier series expansion to Eqs. (25) and (26) along the boundary, the boundary conditions along the inner and outer surfaces are expanded in the form of double Fourier series. When a plate is symmetric about more than one axis, the boundary conditions, in the case of symmetric mode can be written in the form of a matrix as given below:
are given in the Appendix A.Performing the Fourier series expansion to Eqs. (25) and (26) along the boundary, the boundary conditions along the inner and outer surfaces are expanded in the form of double Fourier series. When a plate is symmetric about more than one axis, the boundary conditions, in the case of symmetric mode can be written in the form of a matrix as given below: | (32) |
where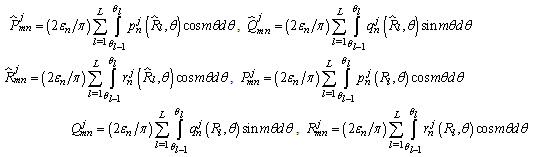 | (33) |
Similarly, the matrix for the antisymmetric mode is obtained as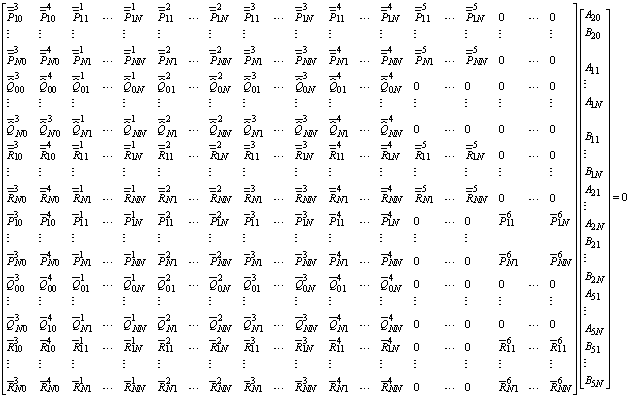 | (34) |
where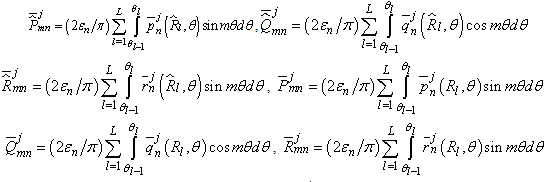 | (35) |
and where 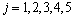 and
and  ,
, 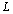 is the number of segments,
is the number of segments,  is the coordinate
is the coordinate 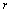 at the inner boundary,
at the inner boundary, 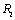 is the coordinate
is the coordinate 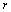 at the outer boundary and N is the number of truncation of the Fourier series. For the nontrivial solution of the systems of equations given in Eqs. (32) and (34), the determinant of the coefficient matrix must vanish and these determinants give the frequencies of symmetric and antisymmetric modes respectively.
at the outer boundary and N is the number of truncation of the Fourier series. For the nontrivial solution of the systems of equations given in Eqs. (32) and (34), the determinant of the coefficient matrix must vanish and these determinants give the frequencies of symmetric and antisymmetric modes respectively.
6. Particular Case
The frequency equations for a ring shaped plate of polygonal cross-sections is obtained by omitting the fluid medium in the corresponding expressions and solutions of the above sections. This frequency equations are further reduced to obtain the frequency equations of a solid polygonal cross-sectional plate by considering the outer surface of the plate 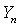 and
and 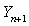 are equal to zero in the Eqs. (25) and (26), this frequency equations are matches well with the frequency equations of Ponnusamy[5] by considering the thermal fields are equal to zero. Using this frequency equation, the numerical results of the frequency for a plate in space is obtained, this results is used to compare with the frequency obtained for a plate immersed in fluid.
are equal to zero in the Eqs. (25) and (26), this frequency equations are matches well with the frequency equations of Ponnusamy[5] by considering the thermal fields are equal to zero. Using this frequency equation, the numerical results of the frequency for a plate in space is obtained, this results is used to compare with the frequency obtained for a plate immersed in fluid.
7. Numerical Results and Discussions
In order to illustrate the nature and general behavior of the solution, some numerical examples are considered in this section. The resulting frequency equations of the symmetric and antisymmetric cases of the ring shaped plate of polygonal cross sections immersed in a fluid given in Eqs. (33) and (35) are transcendental in nature with respect to the dimensionless frequency 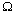 . The computation of Fourier coefficients given in Eqs. (34) and (36) is carried out using the five point Gaussian quadrature. To obtain the roots of the frequency equation, the secant method applicable for the complex roots (Antia[12]) is employed. The material properties used for the computations are as follows: for solid, the Poisson ratio
. The computation of Fourier coefficients given in Eqs. (34) and (36) is carried out using the five point Gaussian quadrature. To obtain the roots of the frequency equation, the secant method applicable for the complex roots (Antia[12]) is employed. The material properties used for the computations are as follows: for solid, the Poisson ratio 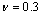 , density
, density 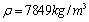 and Young’s modulus
and Young’s modulus 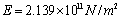 and for fluid the density
and for fluid the density 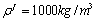 and phase velocity
and phase velocity 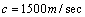 .
.
7.1. Geometrical Relations of Ring Shaped Polygonal Cross-Sections
The geometrical relations for the ring shaped plate of polygonal cross-section given by Nagaya[3] as follows.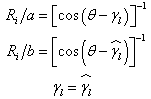 | (36) |
where 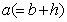 and
and 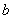 is the apothems,
is the apothems, 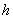 is the thickness of the plate. Here the apothem
is the thickness of the plate. Here the apothem 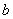 is taken as the reference length which is used to obtain the dimensionless expressions, and
is taken as the reference length which is used to obtain the dimensionless expressions, and 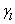 is the angle between the reference axis and the normal to the segment.
is the angle between the reference axis and the normal to the segment.
7.2. Longitudinal Mode
In longitudinal mode of square and hexagonal cross-section, the cross-section vibrates along the axis of the cylinder, so that the vibration displacements in the cross-sections are symmetrical about both the major and the minor axes. Hence the frequency equations are obtained by choosing both the terms of 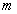 and
and 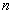 as
as 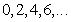 in the Eq. (32) for the numerical calculations. In the case of triangle and pentagonal cross-sectional plate, the vibration and displacements are symmetrical about the major axis alone, hence the frequency equations are obtained from the Eq. (32) by choosing
in the Eq. (32) for the numerical calculations. In the case of triangle and pentagonal cross-sectional plate, the vibration and displacements are symmetrical about the major axis alone, hence the frequency equations are obtained from the Eq. (32) by choosing 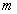 and
and 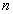 as
as 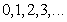 . Since the boundary of the cross-sections namely, triangle, square, pentagon and hexagon are irregular, it is difficult to satisfy the boundary conditions along the curved surface, and hence Fourier expansion collocation method is applied. That is the curved surface, in the range
. Since the boundary of the cross-sections namely, triangle, square, pentagon and hexagon are irregular, it is difficult to satisfy the boundary conditions along the curved surface, and hence Fourier expansion collocation method is applied. That is the curved surface, in the range 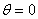 and
and 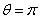 is divided into 20 segments, such that the distance between any two segments is negligible and the integrations is performed for each segment numerically by using the Gauss five point formula .The non-dimensional frequencies are computed for
is divided into 20 segments, such that the distance between any two segments is negligible and the integrations is performed for each segment numerically by using the Gauss five point formula .The non-dimensional frequencies are computed for 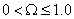 , using the secant method (applicable for the complex roots, (Anita[12] )).
, using the secant method (applicable for the complex roots, (Anita[12] )).
7.3. Flexural Mode
In flexural mode of square and hexagonal cross-section, the vibration and displacements are antisymmetrical about the major axis and symmetrical about the minor axis. Hence the frequency equation may be obtained from Eq. (34) by choosing 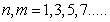 In the case of triangle and pentagonal cross-sections, the vibration and displacements are antisymmetrical about the minor axis, hence the frequency equations may be obtained from Eq. (34)by choosing
In the case of triangle and pentagonal cross-sections, the vibration and displacements are antisymmetrical about the minor axis, hence the frequency equations may be obtained from Eq. (34)by choosing 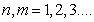
7.4. Comparison between the Frequency Responses of Plate in Space and Plate Immersed in Fluid
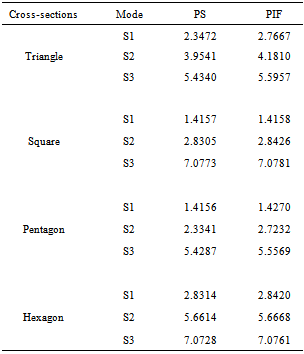
Table 1. Comparison between non-dimensional frequencies of Plate in Space (PS) and Plate Immersed in Fluid (PIF) for longitudinal modes of the Polygonal (triangle, square, pentagon and hexagon) cross-sectional plates
 |
| |
|
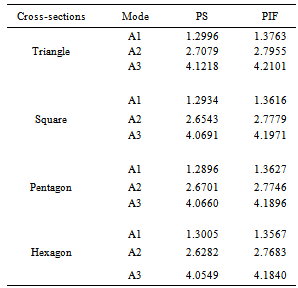
A comparison is made between the non-dimensional frequencies of Plate in Space (PS) and Plate Immersed in Fluid (PIF) for the longitudinal and flexural anti symmetric modes of vibrations and are shown in Tables 1 and 2 respectively. From the Tables 1 and 2, it is observed that, the non-dimensional frequencies increases for increasing modes of vibrations. Comparing the frequency responses of PS and PIF, the frequencies are higher for a plate immersed in fluid than the plate in space, this is the proper physical behavior for solid-fluid interface problems. The notations namely S1, S2, S3 and A1, A2, A3 used in the Tables respectively represents the symmetric and anti symmetric modes of vibration, and the number 1, 2, 3 represents the first, second and third modes of vibrations.Table 2. Comparison between non-dimensional frequencies of Plate in Space (PS) and Plate Immersed in Fluid (PIF) for flexural anti symmetric modes of the Polygonal (triangle, square, pentagon and hexagon) cross-sectional plates
 |
| |
|
7.5 Dispersion Curves
The frequency responses of longitudinal and flexural antisymmetric modes of vibration are plotted in the form of dispersion curves. The notations used in the figures, namely, PS, PF respectively denotes the plate in space and plate immersed in fluid. The notations 1, 2 and 3 respectively represcents the first, second and third modes of vibrations. The cross over points in various dispersion curves of different modes indicate that for a particular frequency of vibrations, the mechanical energy is communicated between the directions of frequency in the respective modes. Another aspect, which can be seen from the graph is that the frequencies are increases with respect to its modes of vibration. It is also observed that the displacement of particles takes irregular path when a plate in space (vacuum).A dispersion curve is drawn to compare the frequency responses of longitudinal modes of triangular cross-sectional plate immersed in fluid and in space and is shown in Fig.1. From the Fig.1, it is observed that, the non-dimensional frequencies are increased with respect to its modes of vibrations and also the frequencies are linearly increased for a plate immersed in fluid. Similarly, a comparison is made between the frequency responses of flexural antisymmetric modes of triangular cross-sectional plate immersed in fluid and in space and is shown in Fig.2. From Fig.2, it is observed that the displacement of particles for a plate immersed in fluid and in space receive a similar pattern. The displacement of energy for a plate in space is lesser than the plate immersed in fluid.Figs.3 and 4 respectively shows the comparison between the frequency responses of longitudinal and flexural antisymmetric modes of square cross-sectional plate immersed in fluid and in space. From the Figs.3 and 4, it is observed that, the non-dimensional frequencie increases with respect to its modes of vibrations. From the Fig.3, for the first and third modes of vibrations, the frequencies will be the same for a particular period, after that both the plate immersed in fluid and in space have dispersion in different patterns. A similar type of behavior is observed for the flexural antisymmetric modes of vibrations also. | Figure 1. Comparison between the non-dimensional frequencies of longitudinal modes of triangular cross-sectional plate immersed in fluid and in space |
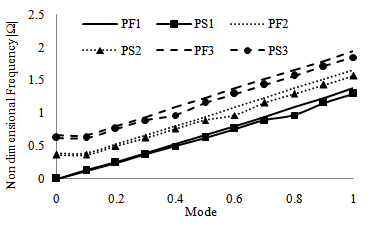 | Figure 2. Comparison between the non-dimensional frequencies of triangular cross-sectional plate immersed in fluid and in space for different flexural anti symmetric modes |
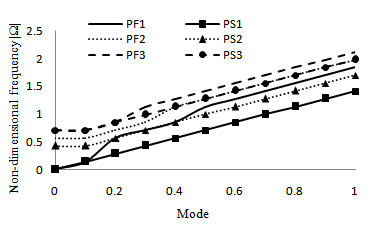 | Figure 3. Comparison between the frequencies of flexural anti symmetric modes of square cross sectional plate immersed in fluid and in space |
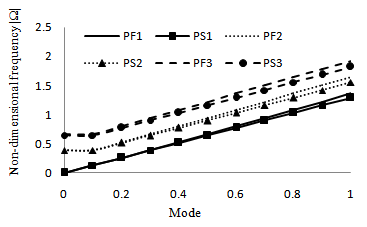 | Figure 4. Comparison between the frequencies of longitudinal modes of square cross sectional plate immersed in fluid and in space |
Graph is drawn to compare the frequencies of longitudinal and flexural antisymmetric modes of vibration for pentagonal cross-sectional plate immersed in fluid and in space is respectively and is shown in the Figs.5 and 6. 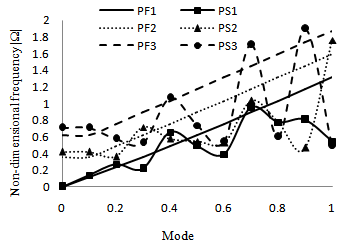 | Figure 5. Comparison between the frequencies of longitudinal modes of pentagonal cross sectional plate immersed in fluid and in space |
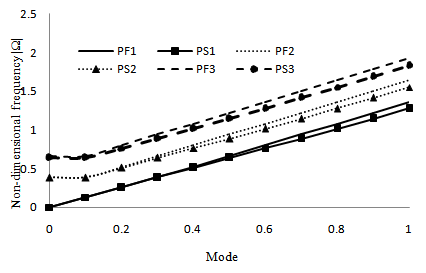 | Figure 6. Comparison between the frequencies of flexural anti symmetric modes of pentagonal cross-sectional plate immersed in fluid and in space |
The dispersion of a plate immersed in fluid linearly increases, whereas the dispersion pattern is irregular when the plate is in space. The cross-over points between the modes of vibration indicates that, there is a transfer of energy between the modes of vibrations. The plate is highly dispersive when it is placed in vacuum. A comparison graph is drawn between the non-dimensional frequencies of longitudinal and flexural anti symmetric modes of hexagonal plates and are shown in the Figs. 7 and 8 respectively. From the Figs. 7 and 8, it is observed that the non-dimensional frequencies are higher for plate immersed in fluid than the plate is space. This is the proper physical behavior of solid-fluid interaction problems. 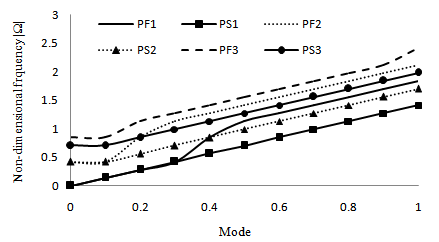 | Figure 7. Comparison between the non-dimensional frequencies of longitudinal modes of hexagonal cross sectional plate immersed in fluid and in space |
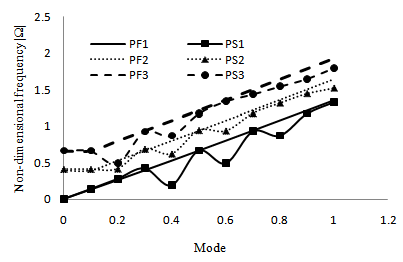 | Figure 8. Comparison between the non-dimensional frequencies of flexural anti symmetric modes hexagonal cross sectional plate immersed in fluid and in space |
8. Conclusions
The in-plane vibration of rings of polygonal cross section composed of homogeneous isotropic material immersed in a fluid is analyzed using the Fourier expansion collocation method. The frequency equations are obtained for longitudinal and flexural antisymmetric modes of vibrations. The computed non-dimensional frequencies for PS and PIF are compared by plotting the dispersion curves. Comparison is made between non-dimensional frequencies of Plate in Space (PS) and Plate Immersed in Fluid (PIF) for longitudinal modes of the Polygonal (triangle, square, pentagon and hexagon) cross-sectional plates.
ACKNOWLEDGEMENTS
The author thanks the reviewers for their suggestions to develop the paper in successful form.
Appendix A
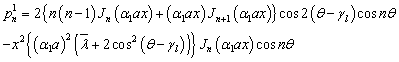 | (A1) |
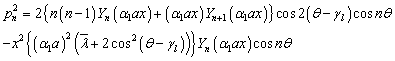 | (A2) |
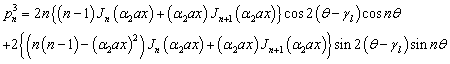 | (A3) |
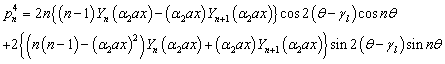 | (A4) |
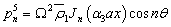 | (A5) |
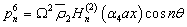 | (A6) |
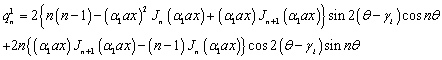 | (A7) |
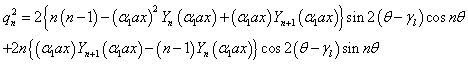 | (A8) |
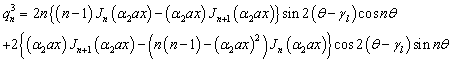 | (A9) |
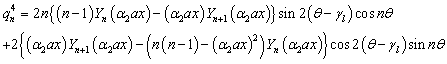 | (A10) |
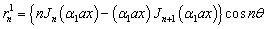 | (A11) |
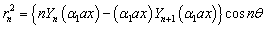 | (A12) |
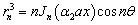 | (A13) |
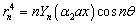 | (A14) |
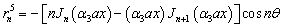 | (A15) |
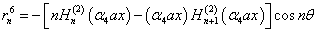 | (A16) |
The barred expressions for the anti symmetric case are obtained by replacing 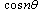 by
by 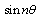 and
and 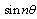 by in the Appendix A.
by in the Appendix A.
References
| [1] | Nagaya, K. Simplified Method for solving problems of vibrating plates of doubly connected arbitrary shape. Part I: Derivation of the frequency equation. J.Sound and Vib. 1981, 74(4), 543-551. |
| [2] | Nagaya, K. Simplified method for solving problem of vibrating plates of doubly connected arbitrary shape. Part II: Applications and experiments. J. Sound and Vib. 1981, 74(4), 553-564. |
| [3] | Nagaya, K. Vibration of a thick polygonal ring in its plane. J. Acoust. Soc. Am., 1983b, 74(5), 1441-1447. |
| [4] | Ponnusamy, P. Wave propagation in thermo-elastic plate of arbitrary cross-sections. J. Multidiscipline Modelling in Materials and Structures. 2011, 7(3), 329-350. |
| [5] | Ponnusamy, P. Dispersion analysis of generalized thermo elastic plate of polygonal cross-sections. J. Appl. Mathematical Modeling. 2012, 36, 3343-3358. |
| [6] | Venkatesan, M and Ponnusamy, P. Wave Propagation in a solid cylinder of arbitrary cross-section immersed in a fluid, J. Acoust. Soc. Am. 2002, 112, 936-942. |
| [7] | Venkatesan, M. and Ponnusamy, P. Wave Propagation in a generalized thermo elastic solid cylinder of arbitrary cross-section immersed in a fluid. Int. J. Mech. Science. 2007, 49, 741-751. |
| [8] | Sinha, K., Plona, J., Kostek, S. and Chang, S. Axisymmetric wave propagation in a fluid-loaded cylindrical shells. I: Theory; II Theory versus experiment. J. Acoust. Soc. Am. 1992, 92, 1132-1155. |
| [9] | Berliner, J. and Solecki, R. Wave Propagation in a fluid-loaded, transversely isotropic cylinders. Part I. Analytical formulation; Part II Numerical results, J. Acoust. Soc. Am., 1996, .99, 1841-1853. |
| [10] | Easwaran , V and Munjal, M.L. A note on the effect of wall compliance on lowest-order mode propagation in a fluid-filled/submerged impedance tubes. J. Acoust. Soc. Am. 1995, 97(6), 3494-3501. |
| [11] | Achenbach, J.D. Wave Propagation in Elastic Solids, Elsevier Publishing Company Inc., New York, 1973. |
| [12] | Antia, H Numerical Methods for Scientists and Engineers, Hindustan Book Agency, New Delhi, 2002. |

 is zero. To satisfy the boundary conditions, the Fourier expansion collocation method is performed to the equations of the boundary conditions along the boundary of the inner and outer surface of the ring. Also, the frequency equations are obtained for the symmetric and antisymmetric cases. To illustrate the validity of the model, some numerical examples are provided for the frequency equation. The equation is solved by omitting the fluid medium and the results are compared with the frequency responses of plate in space and plate immersed in fluid. Also, the results are obtained for polygonal ( triangle, square, pentagon and hexagon) rings for the longitudinal and flexural antisymmetric modes of vibrations.
is zero. To satisfy the boundary conditions, the Fourier expansion collocation method is performed to the equations of the boundary conditions along the boundary of the inner and outer surface of the ring. Also, the frequency equations are obtained for the symmetric and antisymmetric cases. To illustrate the validity of the model, some numerical examples are provided for the frequency equation. The equation is solved by omitting the fluid medium and the results are compared with the frequency responses of plate in space and plate immersed in fluid. Also, the results are obtained for polygonal ( triangle, square, pentagon and hexagon) rings for the longitudinal and flexural antisymmetric modes of vibrations.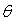 in an arbitrary point inside the plate and denote the displacements
in an arbitrary point inside the plate and denote the displacements 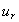 in the direction of r and
in the direction of r and 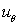 in the tangential direction
in the tangential direction 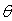 . The in-plane vibration and displacements of ring shaped plate of polygonal cross-sections immersed in fluid is obtained by assuming that there is no vibration and displacement along the z-directions in the cylindrical coordinate system
. The in-plane vibration and displacements of ring shaped plate of polygonal cross-sections immersed in fluid is obtained by assuming that there is no vibration and displacement along the z-directions in the cylindrical coordinate system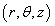 . The two dimensional stress equations of motion, strain displacement relations in the absence of body forces for a linearly elastic medium are considered from Ponnusamy[4] as
. The two dimensional stress equations of motion, strain displacement relations in the absence of body forces for a linearly elastic medium are considered from Ponnusamy[4] as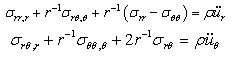
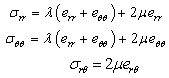
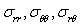 are the stress components,
are the stress components, 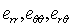 are the strain components,
are the strain components, 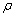 is the mass density,
is the mass density, 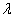 and
and 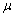 are Lame’s constants. The strain
are Lame’s constants. The strain 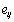 related to the displacements are given by
related to the displacements are given by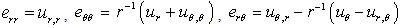
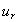 and
and 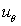 are the displacements components along radial and circumferential directions respectively. The comma in the subscripts denotes the partial differentiation or derivative with respect to the variables.Substituting the Eqs.(2) and (3) in Eqs.(1), the displacement equations of motions are obtained as
are the displacements components along radial and circumferential directions respectively. The comma in the subscripts denotes the partial differentiation or derivative with respect to the variables.Substituting the Eqs.(2) and (3) in Eqs.(1), the displacement equations of motions are obtained as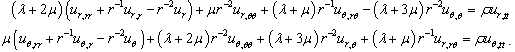
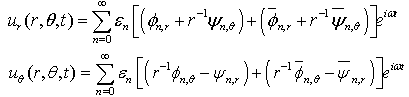
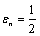 for
for 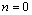 ,
, 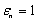 for
for 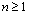 ,
, 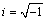 ,
, 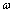 is the frequency,
is the frequency, 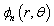 ,
, 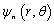 ,
, 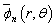 and
and 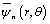 are the displacement potentials. By introducing the dimensionless quantities
are the displacement potentials. By introducing the dimensionless quantities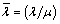 ,
, 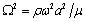 ,
, 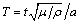 ,
, 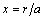 and substituting Eq.(5) in Eq.(4), we obtain
and substituting Eq.(5) in Eq.(4), we obtain 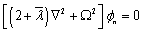
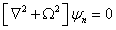
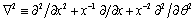 The solution of Eq. (6) for symmetric mode is
The solution of Eq. (6) for symmetric mode is 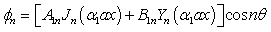
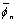 is obtained by replacing
is obtained by replacing 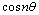 by
by 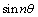 in Eq. (8), we get
in Eq. (8), we get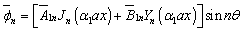
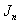 is the Bessel function of first kind of order n and
is the Bessel function of first kind of order n and 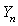 is the Bessel function of second kind of order n and
is the Bessel function of second kind of order n and 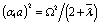 . Solving Eq. (7), we obtain
. Solving Eq. (7), we obtain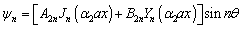
 is obtained from Eq. (10) by replacing
is obtained from Eq. (10) by replacing  by
by 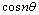 in Eq. (10), we obtain
in Eq. (10), we obtain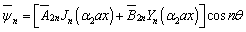
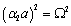 . If
. If 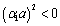 and
and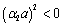 , then the Bessel functions
, then the Bessel functions 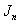 and
and 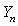 are replaced by the modified Bessel functions
are replaced by the modified Bessel functions 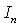 and
and 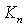 respectively.
respectively.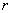 and
and 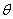 the acoustic pressure and radial displacement equation of motion for an inviscid fluid are of the form Achenbach[11] ,
the acoustic pressure and radial displacement equation of motion for an inviscid fluid are of the form Achenbach[11] ,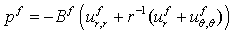
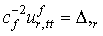
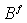 is the adiabatic bulk modulus,
is the adiabatic bulk modulus, 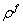 is the density,
is the density, 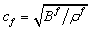 is the acoustic phase velocity in the fluid,
is the acoustic phase velocity in the fluid, 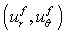 is the displacement vector and
is the displacement vector and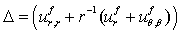
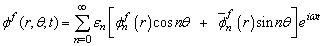
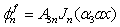
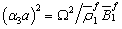 , in which
, in which 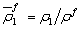 ,
, 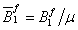 . If
. If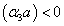 , the Bessel function
, the Bessel function 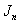 in the Eq. (17) is to be replaced by modified Bessel function
in the Eq. (17) is to be replaced by modified Bessel function 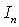 . Similarly, for the outer fluid that represents the oscillatory waves propagating away is given as
. Similarly, for the outer fluid that represents the oscillatory waves propagating away is given as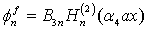
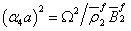 , in which
, in which 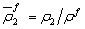 ,
,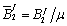 ,
, 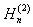 is the Hankel function of the second kind of order n. If
is the Hankel function of the second kind of order n. If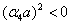 , then the Hankel function of second kind is to be replaced by
, then the Hankel function of second kind is to be replaced by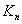 , where
, where 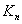 is the modified Bessel function of the second kind. By substituting Eq. (16) in Eq. (12) along with the Eqs. (17) and (18), the acoustic pressure for the inner fluid can be expressed as
is the modified Bessel function of the second kind. By substituting Eq. (16) in Eq. (12) along with the Eqs. (17) and (18), the acoustic pressure for the inner fluid can be expressed as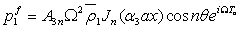
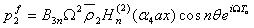
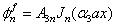
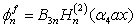
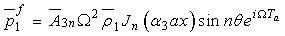
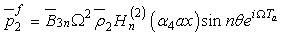
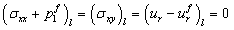
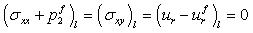
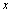 is the coordinate normal to the boundary and
is the coordinate normal to the boundary and 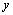 is the coordinate in the tangential direction,
is the coordinate in the tangential direction, 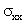 is the normal stress,
is the normal stress, 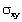 are the shearing stresses and
are the shearing stresses and 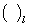 is the value at the
is the value at the 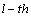 segment of the boundary. The first and last conditions in Eqs. (25) and (26) are due to the continuity of the stresses and displacements of the ring shaped plate and fluid on the curved surfaces. Since the boundary of the cross section is irregular in shape, it is difficult to satisfy the boundary conditions along both inner and outer surfaces of the ring shaped polygonal cross sectional plate immersed in fluid directly. If
segment of the boundary. The first and last conditions in Eqs. (25) and (26) are due to the continuity of the stresses and displacements of the ring shaped plate and fluid on the curved surfaces. Since the boundary of the cross section is irregular in shape, it is difficult to satisfy the boundary conditions along both inner and outer surfaces of the ring shaped polygonal cross sectional plate immersed in fluid directly. If 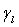 is the angle between normal to the segment and the reference axis and if it is assumed to be constant, then the transformed expressions for the stresses are Nagaya[3] as
is the angle between normal to the segment and the reference axis and if it is assumed to be constant, then the transformed expressions for the stresses are Nagaya[3] as 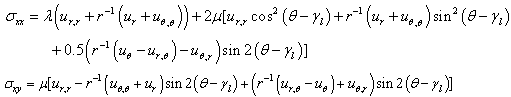
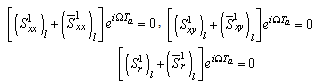
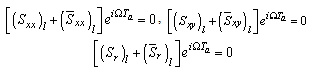
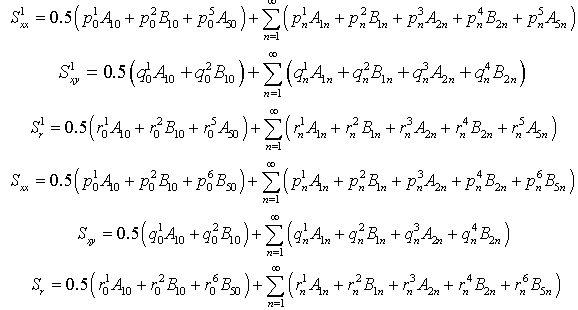
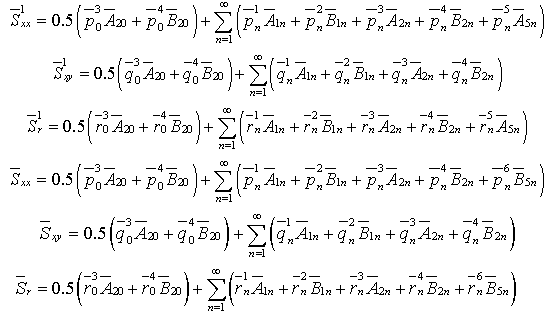
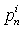 to
to 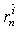 are given in the Appendix A.Performing the Fourier series expansion to Eqs. (25) and (26) along the boundary, the boundary conditions along the inner and outer surfaces are expanded in the form of double Fourier series. When a plate is symmetric about more than one axis, the boundary conditions, in the case of symmetric mode can be written in the form of a matrix as given below:
are given in the Appendix A.Performing the Fourier series expansion to Eqs. (25) and (26) along the boundary, the boundary conditions along the inner and outer surfaces are expanded in the form of double Fourier series. When a plate is symmetric about more than one axis, the boundary conditions, in the case of symmetric mode can be written in the form of a matrix as given below:
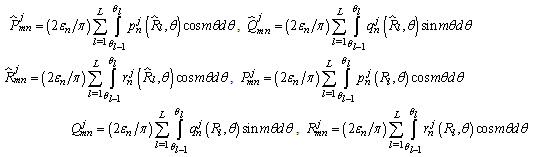

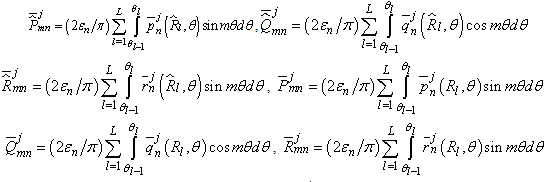
 and
and  ,
, 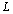 is the number of segments,
is the number of segments,  is the coordinate
is the coordinate 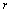 at the inner boundary,
at the inner boundary, 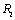 is the coordinate
is the coordinate 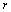 at the outer boundary and N is the number of truncation of the Fourier series. For the nontrivial solution of the systems of equations given in Eqs. (32) and (34), the determinant of the coefficient matrix must vanish and these determinants give the frequencies of symmetric and antisymmetric modes respectively.
at the outer boundary and N is the number of truncation of the Fourier series. For the nontrivial solution of the systems of equations given in Eqs. (32) and (34), the determinant of the coefficient matrix must vanish and these determinants give the frequencies of symmetric and antisymmetric modes respectively.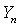 and
and 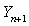 are equal to zero in the Eqs. (25) and (26), this frequency equations are matches well with the frequency equations of Ponnusamy[5] by considering the thermal fields are equal to zero. Using this frequency equation, the numerical results of the frequency for a plate in space is obtained, this results is used to compare with the frequency obtained for a plate immersed in fluid.
are equal to zero in the Eqs. (25) and (26), this frequency equations are matches well with the frequency equations of Ponnusamy[5] by considering the thermal fields are equal to zero. Using this frequency equation, the numerical results of the frequency for a plate in space is obtained, this results is used to compare with the frequency obtained for a plate immersed in fluid.  . The computation of Fourier coefficients given in Eqs. (34) and (36) is carried out using the five point Gaussian quadrature. To obtain the roots of the frequency equation, the secant method applicable for the complex roots (Antia[12]) is employed. The material properties used for the computations are as follows: for solid, the Poisson ratio
. The computation of Fourier coefficients given in Eqs. (34) and (36) is carried out using the five point Gaussian quadrature. To obtain the roots of the frequency equation, the secant method applicable for the complex roots (Antia[12]) is employed. The material properties used for the computations are as follows: for solid, the Poisson ratio 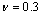 , density
, density 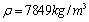 and Young’s modulus
and Young’s modulus 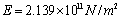 and for fluid the density
and for fluid the density 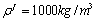 and phase velocity
and phase velocity 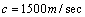 .
. 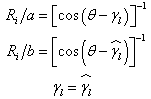
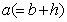 and
and 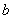 is the apothems,
is the apothems, 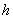 is the thickness of the plate. Here the apothem
is the thickness of the plate. Here the apothem 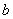 is taken as the reference length which is used to obtain the dimensionless expressions, and
is taken as the reference length which is used to obtain the dimensionless expressions, and 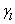 is the angle between the reference axis and the normal to the segment.
is the angle between the reference axis and the normal to the segment.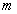 and
and 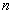 as
as 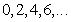 in the Eq. (32) for the numerical calculations. In the case of triangle and pentagonal cross-sectional plate, the vibration and displacements are symmetrical about the major axis alone, hence the frequency equations are obtained from the Eq. (32) by choosing
in the Eq. (32) for the numerical calculations. In the case of triangle and pentagonal cross-sectional plate, the vibration and displacements are symmetrical about the major axis alone, hence the frequency equations are obtained from the Eq. (32) by choosing 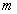 and
and 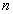 as
as 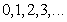 . Since the boundary of the cross-sections namely, triangle, square, pentagon and hexagon are irregular, it is difficult to satisfy the boundary conditions along the curved surface, and hence Fourier expansion collocation method is applied. That is the curved surface, in the range
. Since the boundary of the cross-sections namely, triangle, square, pentagon and hexagon are irregular, it is difficult to satisfy the boundary conditions along the curved surface, and hence Fourier expansion collocation method is applied. That is the curved surface, in the range 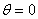 and
and 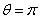 is divided into 20 segments, such that the distance between any two segments is negligible and the integrations is performed for each segment numerically by using the Gauss five point formula .The non-dimensional frequencies are computed for
is divided into 20 segments, such that the distance between any two segments is negligible and the integrations is performed for each segment numerically by using the Gauss five point formula .The non-dimensional frequencies are computed for 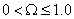 , using the secant method (applicable for the complex roots, (Anita[12] )).
, using the secant method (applicable for the complex roots, (Anita[12] )).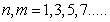 In the case of triangle and pentagonal cross-sections, the vibration and displacements are antisymmetrical about the minor axis, hence the frequency equations may be obtained from Eq. (34)by choosing
In the case of triangle and pentagonal cross-sections, the vibration and displacements are antisymmetrical about the minor axis, hence the frequency equations may be obtained from Eq. (34)by choosing 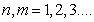








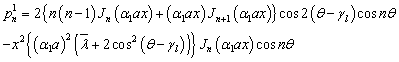
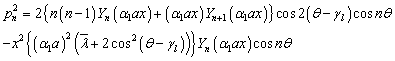
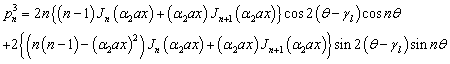
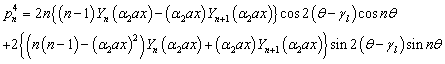
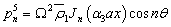
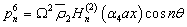
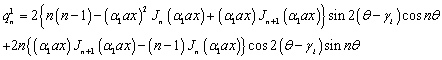
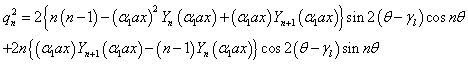
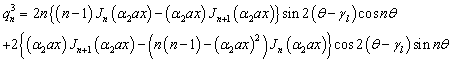
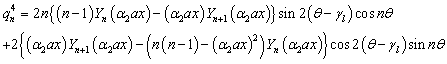
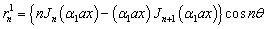
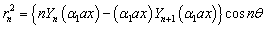
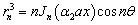
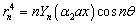
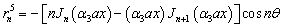
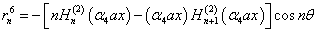
 by
by  and
and  by in the Appendix A.
by in the Appendix A. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
