1. Introduction

On the example of the prolate and oblate ideal spheroids are calculated the angular correlation functions these scatterers at the basis of the union of the theory of the diffraction and the theory of the accident fields.

2. The Theory of the Sound Scattering by the Accident Orientated Ideal Bodies of the Spheroidal Forms

Let the spheroidal scatterer is found in the centre of the sector group of the hydrophones and he is orientated accident, only hydrophon is appeared by the sound radiator (fig. 1), he radiates the harmonic sound signal of the frequency 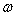. The reflected of the body the signal is the multiplicative signal, consisting of the accidental and determinate parts. The determinate component can separate from the accidental component. We will suppose the accidental component by fixed and homogeneous[1]. The angular correlation function of the fixed and homogeneous accidental field has the following appearance[2]:

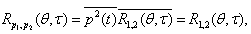(1)

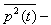where: the middle square of the sound pressure; 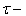the temporal interval between the signals (by us 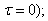the line over the function 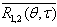means the averaging.

The angular space correlation function 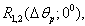setting the communication between hydrophones 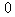and 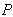, has appearance:

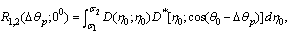(2)

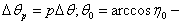where: the angle of the illumination; and 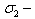the cosines of the critical angles of the illumination; 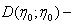the angular characteristic of the sound reflection in the direction at the source; * - means the complex conjugate quantity.

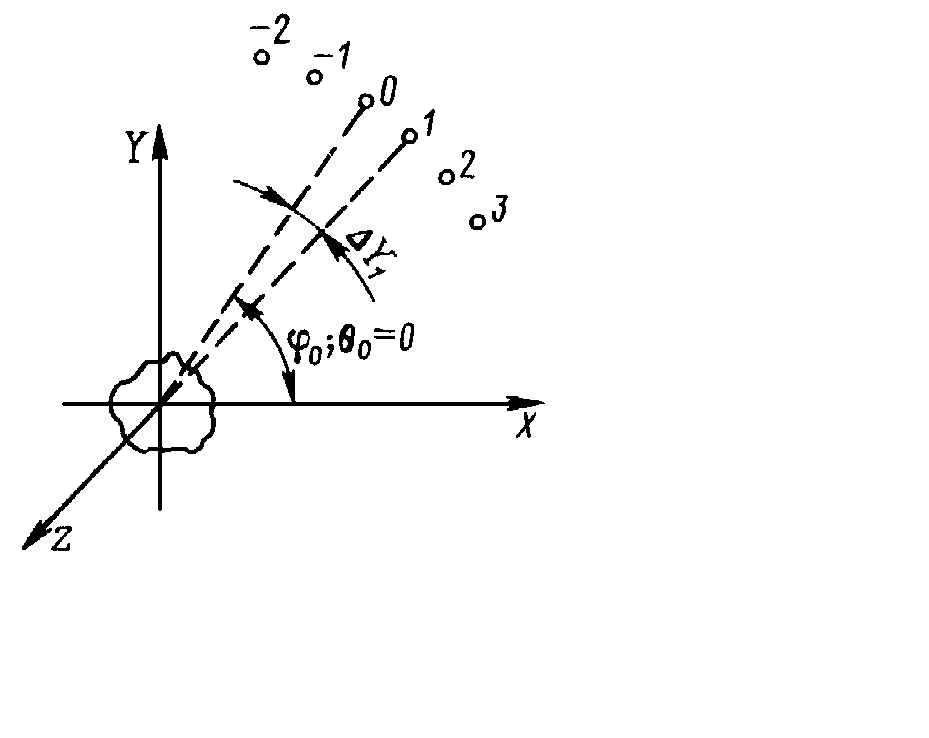Figure 1. The orientation of the scatterer relatively of the source and the hydrophones

3. The Results of the Calculations of the Correlation Functions of the Ideal Spheroids (Prolate And Oblate)

At the base (2) were calculated the angular correlation functions of the soft and hard, prolate and oblate spheroids. For the soft prolate spheroid the angular characteristic of the scattering will have appearance[3]:

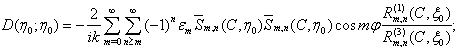(3)

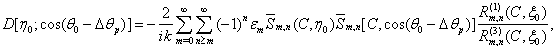(4)

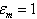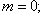
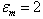where: by by 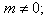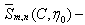the angular spheroidal function; 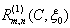and 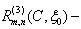the radial spheroidal functions first and third genders; 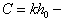the wave size, 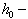semi-focal distance, 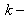the wave number in the liquid; 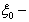the radial spheroidal coordinate of the scatterer.

The correlation functions were calculated in the limits from 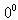to 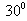with the step 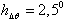for the wave sizes 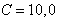and 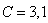. The results of the calculations of the moduluses of the angular correlation functions of the sound scattering by the hard 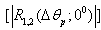(the curve 1) and soft 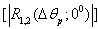(the curve 2) oblate spheroids for 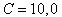are introduced at fig. 2 ( the angles of the intensive scattering).

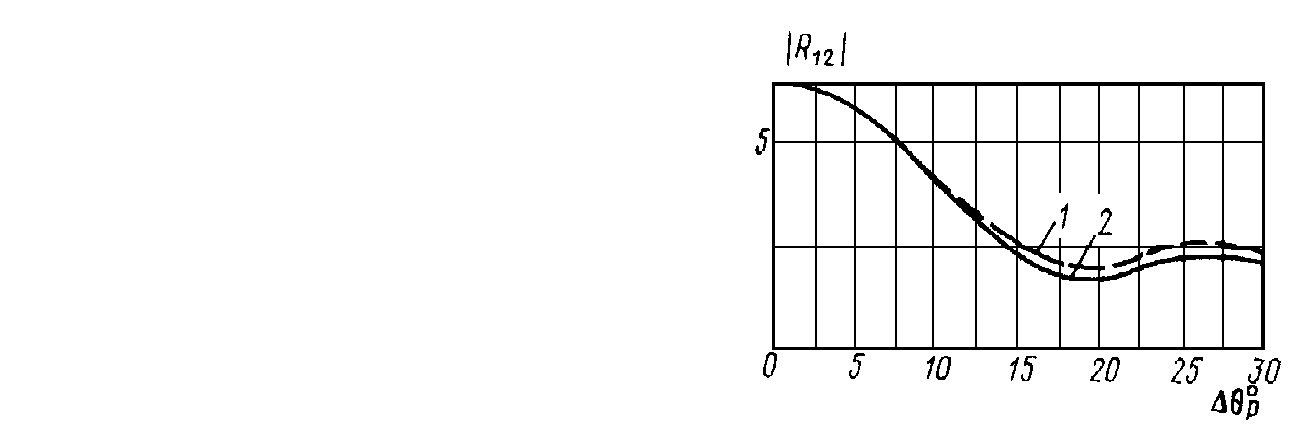Figure 2. The moduluses of the angular correlation functions of the oblate spheroids

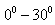For the examination of the hypothesis against homogeneous of the accident scattered field ( in limits of the sector for the prolate spheroid were calculated the correlation functions 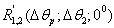and 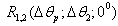relatively the zero hydrophone 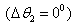and hydrophones with the angular position 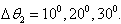At fig. 3 are shown the moduluses of the angular correlation functions of the prolate spheroid (soft and hard) by 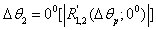(the curve 1) and 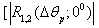(the curve 2) and by 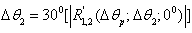(the curve 3) and 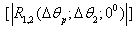(the curve 4) for the angles of the intensive scattering by

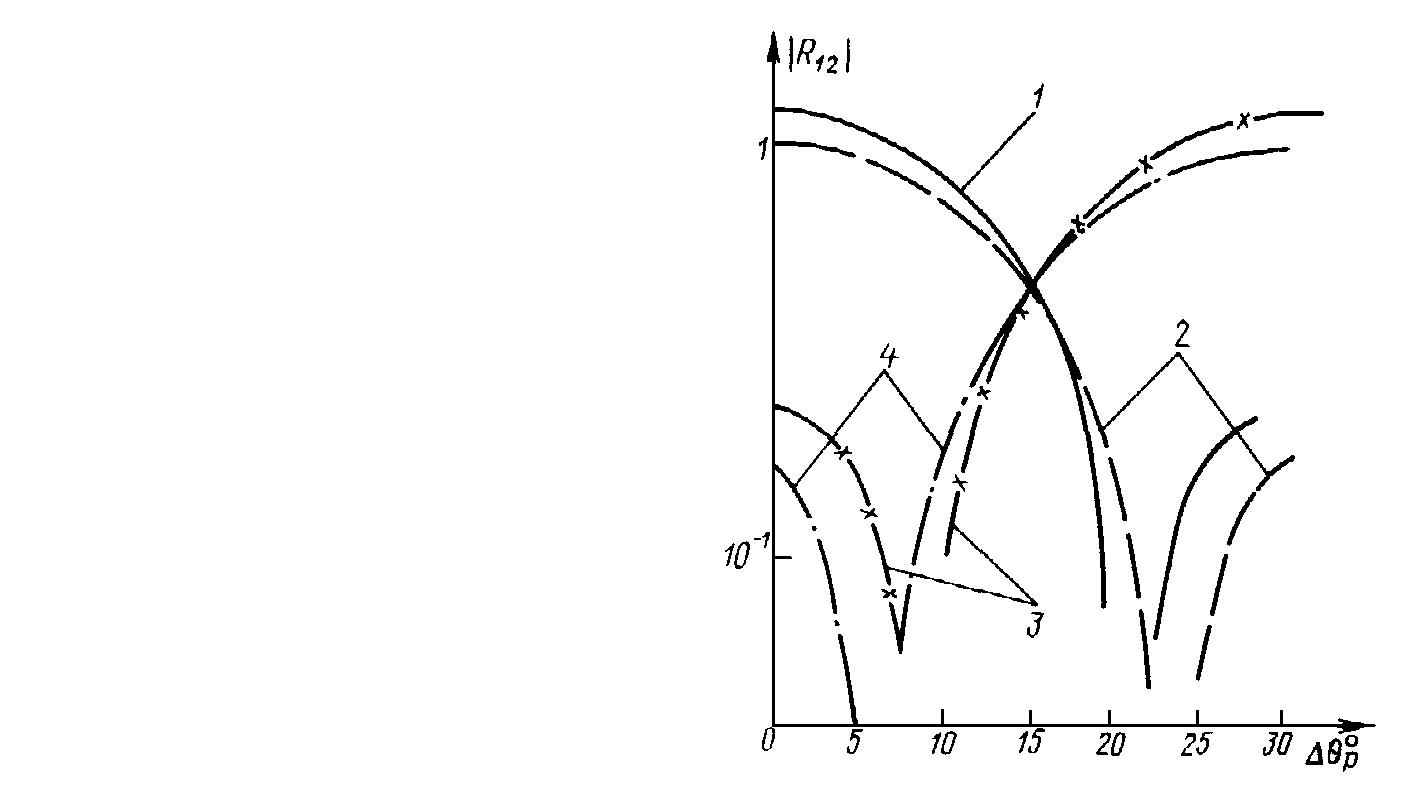Figure 3. The moduluses of the angular correlation functions of the prolate spheroids (by the angles of the intensive scattering)

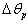How may see from the plots, the moduluses of the angular correlation functions equally depend on the angle only the maximums of this functions displace at the angle 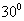what confirms of the hypothesis against of the homogeneous of the accident scattered field in this case. For the angles of the weak scattering the hypothesis against of the homogeneous of the accident scatte-red field don’t appear yust already by 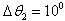From the curves of the fig. 4, relating to this condition, we see, what by the transition from 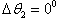by 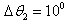is reversed the form of the angular correlation functions.

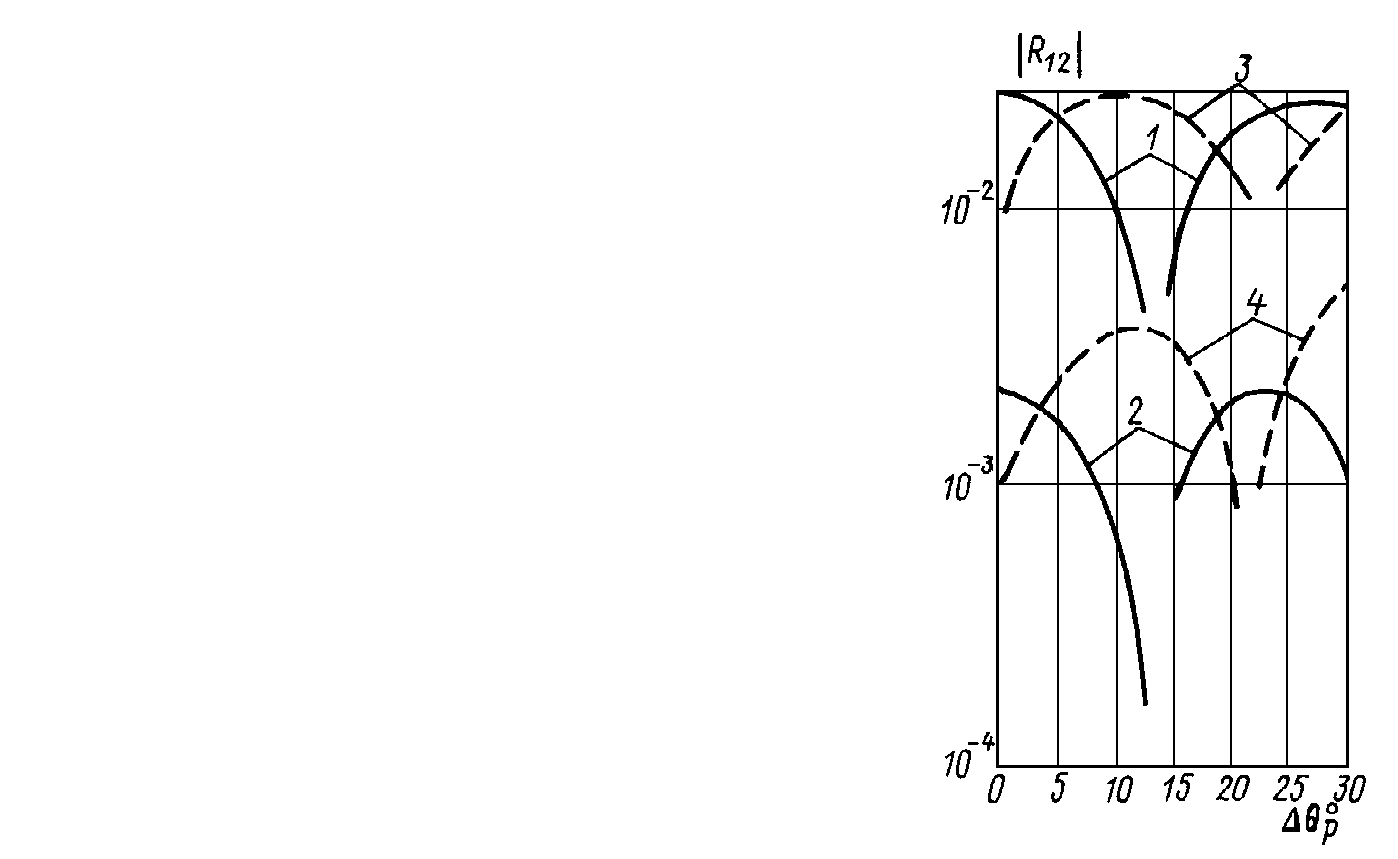Figure 4. The moduluses of the angular correlation functions of the prolate spheroids (by the angles of the weak scattering)/

4. Conclusions

With the help of the theory of the accident processes and fields and the theory of the sound diffraction for the first time were calculated the angular correlation functions of the soft and hard, prolate and oblate spheroids, oriented accident for the angles of the intensive and weak scattering.

ACKNOWLEDGMENTS

This work was supported as part of research under State Contract no P242 of April 21, 2010, within the Federal Target Program «Scientific and scientific – pedagogical personnel of innovative Russia for the years 2009 – 2013”.