1. Introduction

The author gives some procedure using co-ordinate system to solve every problem of virtual work. During my experience in teaching to students I come across that the students find difficulties to choose proper sign of the displacement and force. This simple procedure will eliminate these difficulties

2. Methods

Take proper coordinates of the points where the active forces act.

In the co-ordinate(x,y) ,take proper sign of the active forces, e.g. the force P is here negative. And the displacement yA = -a sinθ is also negative (θ is here acute angle)

Take derivative of yA and multiply it by –P(acting at A) which will yield virtual work (-P(+dyA)). Assume dyA as positive. Do not take –dyA and multiply it by –P.

Multiply +dx_B, +dy_A with the proper sign of associated forces and equate the sum(the total virtual work) to zero.

If any force acts making an angle with the chosen coordinate(x,y), then resolve the forces in the x and y directions.

2.1. Examples 1

In fig 1 the bar AB can rotate about Z axis. Find out the value of Q for which the bar will remain in equilibrium. Take length OA = a, OB = b

Solution :

y_A = -a sinθ,

or, dy_A = -a cosθ d θ

or,

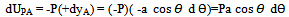(1)

again x_B = + b cosθ

or, dx_B = -b sinθ d θ

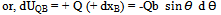(2)

From the principle of virtual work, we can write:

dU_PA + dU_QB = 0

inserting the values from (1) & (2) we get,

Pa cosθ d θ -Qb sinθ dθ = 0

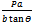or, Q= Ans. (angle BOX = θ)

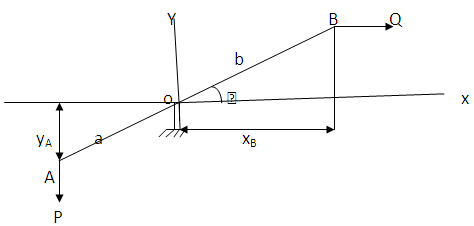Figure 1. The bar AB can rotate about Z axis

2.2. Example 2

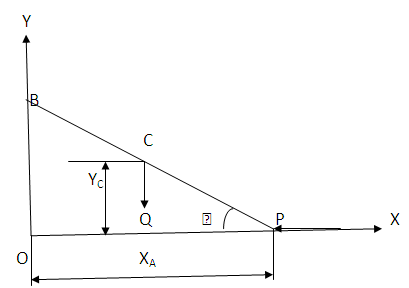
The slider crank mechanism shown in fig 2 has l = 2r and θ = 60⁰ . Find out the ratio Q/P for the system to be in equilibrium.

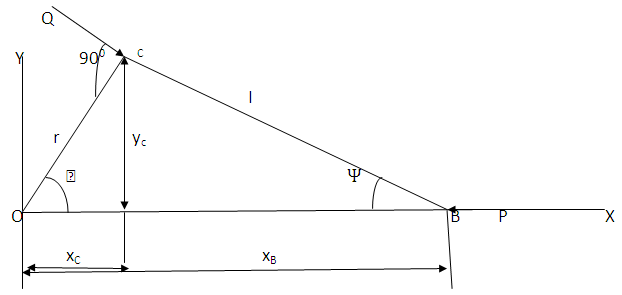Figure 2. Slider crank mechanism

Solution : The coordinate of C ( r cosθ r sinθ and the coordinate of

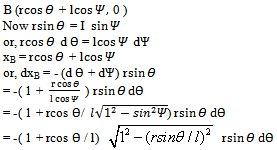Thus virtual work done by the force –P acting at B is

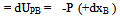(1)

Again to find dU_Qc , We resolve force Q in x and y directions.

X component of Q is Q sinθ and y component of Q is – Q cosθ

x_c = r cosθ

or, dx_C =

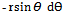Work done by force Q sinθ =Q sinθ (+dx_C )=-Qr Sin² θ dθ

y_C = r sinθ

dy_C =

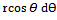Work done by force – Q cosθ = (– Q cosθ dy_c = -Qr Cos² θ dθ

Thus total work done by force Q at C is =

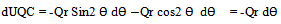(2)

From the principle of virtual work we can write,

dUPB + dUQC = 0 which gives

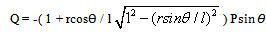For θ = 600 and l = 2r we get Q = 1.1062 P Ans.

(angle cox = θ)

2.3. Example 3

Figure 3. Bar BP in equilibrium

BC = CP = l/2 , To find force P in terms of force Q and angle θ for the equilibrium of the bar BP.

XA = l cosθ , or dXA= - l sinθd θ

Thus work done by force P = - P dXA = P l sinθd θ

Again

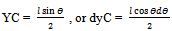Thus work done by force Q = -Q dyC =

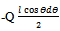So total work done = dU = P l sinθdθ-Q ,

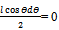Or, P = 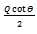Ans. (angle BPO = θ)

2.4. Example 4

We have to prove that for equilibrium the force Q is half of the force P.

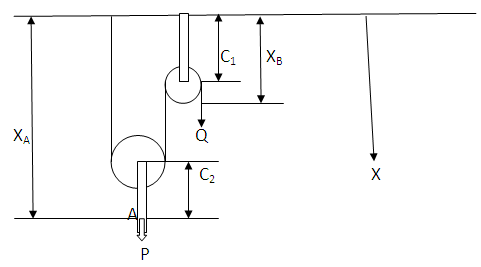Figure 4. Pulley system under equilibrium

The length of the chord remains constant, so

X_B – C₁ + ПR₁ + X_A – C₂ – C₁ + ПR₂ + X_A – C₂ = Constant

Or, X_B + 2 X_A = Constant

Or, dx_B = -2dx_A

Thus the total work done by P and Q is

PdX_A + Qdx_B = 0

Or, PdX_A + Q(-2dx_A) = 0

Or, Q = P/2 Proved.

2.5. Example 5

To find the relation between W₁ and W₂ for the equilibrium of the system

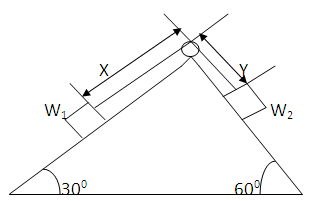Figure 5. Two weights under equilibrium

X + Y = Constant,

Or, dX =- dY

Work done by the force W₁ Sin30⁰ = W₁ Sin30⁰ dx

Work done by the force W₂ Sin60⁰ = W₂ Sin60⁰ dy

Thus W₁ Sin30⁰ dx + W₂ Sin60⁰ dy = 0

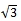W₁ = W₂ Ans.

3. Results

The results of the methods referred here in this article are evident. Author has given five examples and the answers are achieved which are correct by using this method.

4. Discussion

The author has validated the methods taking five examples. The readers are requested to use this easy method in other problems of virtual work .And feel free to contact the author at dilip.adhwarjee@bcrec.org

5. Conclusions

According to the author the method can be applied to all problems involving virtual work.